Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 13. -

Вып. 1. - 2014. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/TITL-41.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/cont.htm

 

УКД 621.313.333

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ  ИНДУКТОРНЫХ ДВИГАТЕЛЕЙ  ПРИ ИМПУЛЬСНОЙ  ФОРМЕ  ПИТАНИЯ  ОТ  СИНУСОИДАЛЬНОГО ИСТОЧНИКА

 

Ó 2014 г. Кулик Ю. Д.,  Полющенков И. С.

 

(kulik.doc)

 

В работе предлагается математическая модель для тихоходных индукторных двигателей с импульсной формой питания непосредственно от синусоидального источника. Математическое описание учитывает параметрический характер цепи обмотки фазы введением двух параметров: относительного значения основной составляющей индуктивности и соотношения постоянной составляющей индуктивности с активным сопротивлением цепи обмотки фазы. Предлагаемая модель для индукторных двигателей с электромеханической и электромагнитной редукцией позволяет решать инженерные задачи анализа и синтеза для указанных двигателей.

Ключевые слова: сосредоточенная обмотка фазы, вентильная коммутация, электромеханическая и электромагнитная редукция, энергетический коэффициент полезного действия, угол нагрузки.

 

Получение низких частот вращения остается актуальной задачей электромеханики. Альтернативными способами понижения частоты вращения традиционной схеме быстроходный двигатель плюс редуктор являются:

1. Электромеханическая  редукция (механический редуктор совмещается с электромагнитной частью таким образом, что воздействие в передаче  осуществляется на промежуточное звено, минуя быстроходное – на сателлит в планетарной передаче, на гибкий элемент в волновой передаче);

2. Электромагнитная (магнитные структуры статора и ротора выполняются явнополюсными с определенным соотношением между ними).

Группу двигателей с электромеханической редукцией образуют двигатели с катящимся (эксцентрично расположенным) ротором и волновые двигатели. Группу двигателей с электромагнитной редукцией – шаговые двигатели и вентильно-индукторные двигатели.

В основе рассматриваемых в статье индукторных двигателей является использование эффекта взаимодействия ферромагнитного тела с магнитным полем. Представляет интерес для указанных модификаций индукторных двигателей при формировании многофазной импульсной системы от синусоидального источника установить единое математическое описание физических процессов с целью получения необходимых выражений для оценки электромагнитного момента, а также энергетических показателей в целом.

При электромеханической редукции частота вращения выходного вала определяется с помощью выражения

,

(1)

а при электромагнитной

,

(2)

где   N – число одноименных фазных зон в схеме обмотки;

   iр – передаточное отношение механического редуктора;

  ZR = N(сm2 ± 1)  - число зубцов (полюсов) ротора;

   с – число зубцов образующих гребенчатую зону на полюсном выступе (определяется как отношение полюсного деления статора к полюсному делению ротора, при их отсутствии с = 1);

        m2 – число фаз сосредоточенной обмотки статора;

        – синхронная частота перемещения МДС обмотки статора.

При частоте сети  f = 50 Гц и электромеханической редукции можно получать n2 от нескольких десятков до долей оборота в минуту, а при электромагнитной n2 от нескольких сотен до несколько десятков оборотов в минуту.

Полюсные структуры статоров определяются следующими выражениями:

при электромеханической

,

(3)

при электромагнитной

,

(4)

где s – степень расщепления магнитного потока в фазной зоне.

Наличие дополнительных полюсов в  фазной зоне у двигателей с эксцентрично расположенным ротором  преследует цель уменьшения момента инерции ротора, а при волновой передаче - сделать гибкий ротор податливым для перемещения волны деформации. При наличии s катушек в фазной зоне они обычно соединяются между собой так, чтобы создавалась чередующаяся полярность полюсов вдоль всей расточки статора. Такой же принцип построения схемы обмотки статора и порядка включения вентилей в цепях фаз должен быть и при электромагнитной редукции (при этом s = 1).

В случае получения нерегулируемой низкой частоты вращения импульсная система напряжений  может быть сформирована непосредственно от сети переменного тока путем использования в схеме обмотки неуправляемых вентилей (диодов), которую предложил В.П. Наний [1].

На рисунке 1 представлен базовый фрагмент для формирования многофазных обмоток с вентильной коммутацией, который положен в основу предлагаемой математической модели.

Смысл модели сводится к использованию элементов теории электрических цепей для определения энергетических соотношений в указанных двигателях с учетом параметрического характера цепи обмотки фазы.

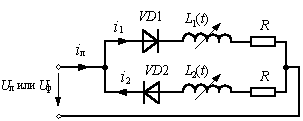
Рисунок 1 – Базовый фрагмент для построения многофазных схем обмоток с

вентильной коммутацией

 

Основные допущения:

1. Изменение индуктивного параметра (индуктивности фаз в зависимости от углового положения ротора) происходит синхронно с изменением напряжения сети и зависит только от углового положения ротора (является независимой функцией времени);

2. Магнитная система слабо насыщена и индуктивные параметры зависят только от соответствующих магнитных проводимостей рабочего зазора;

3. Взаимоиндуктивная связь между сосредоточенными обмотками фаз отсутствует;

4. Вентиль считается идеальным;

5. Сеть имеет бесконечно большую мощность.

Закон изменения индуктивного параметра различен для двигателей с электромеханической и электромагнитной редукцией и может быть представлен в следующем виде:

при электромеханической редукции

,

(5)

при электромагнитной редукции

,

(6)

где

L0 – постоянная составляющая индуктивного параметра (как среднее значение);

 – относительное значение амплитуды переменной составляющей зазора;

 – среднее значение амплитуды переменной составляющей воздушного зазора в фазной зоне обмотки;

 – среднего значение зазора в фазной зоне;

 – средние значения максимального и минимального зазоров в фазной зоне;

– коэффициент основной гармоники индуктивного параметра;

αнач – начальная фаза процесса самокоммутации обмотки фазы.

Учитывая параметрический характер цепи обмотки фазы для всех названных выше вариантов двигателей и сделанные допущения, дифференциальное уравнение для фазного тока имеет вид при 0 ≤ t ≤ tотк:        

,

(7)

где R – активное сопротивление обмотки фазы;

      um – амплитуда синусоидального напряжения;

      αнач – угловая координата (в электрических градусах)  начала момента  коммутации;

      tотк – момент закрытия вентиля.

Однако, как и все дифференциальные уравнения с переменными коэффициентами, уравнение (7) не имеет аналитического решения, поэтому задача сводится к преобразованию его к виду, решение которого можно выполнить, например, методом Рунге-Кутта используя математический пакет MathCAD.

Для варианта двигателей с электромеханической редукцией после подстановки выражения (5) в (7) и дифференцирования получаем

,

 

все члены уравнения делим на R, а второй член левой части уравнения умножаем на . В результате этого получаем:

,

 

вводя   – характеризует соотношение постоянных параметров обмотки фазы и  = ωt – фазовый угол получаем:

.

Обозначая   в окончательном виде дифференциальное уравнение (7) приведено к форме удобной для компьютерного моделирования при  0 ≤ a ≤ aотк: 

,

(8)

Для вентильно-индукторного двигателя после подстановки выражения (6) в (7) и дифференцирования получаем

,

 

также деля на R все члены уравнения и умножая на второго члена левой части получаем

.

Обозначая  окончательно получаем при  0 ≤ a ≤ aотк:

,

(9)

где  aотк – фазовый угол момента закрытия вентиля.

Компьютерное решение уравнения (8) или (9) для мгновенного значения фазного тока с учетом (5) или (6) может быть представлено не только в графическом виде (рисунок 2), но и в виде гармонического ряда

,

(10)

где

       i0 – постоянная составляющая фазного тока;

       ikm – амплитуда k – ой  гармоники фазного тока;

 φk – начальная фаза k – ой  гармоники фазного тока.

 

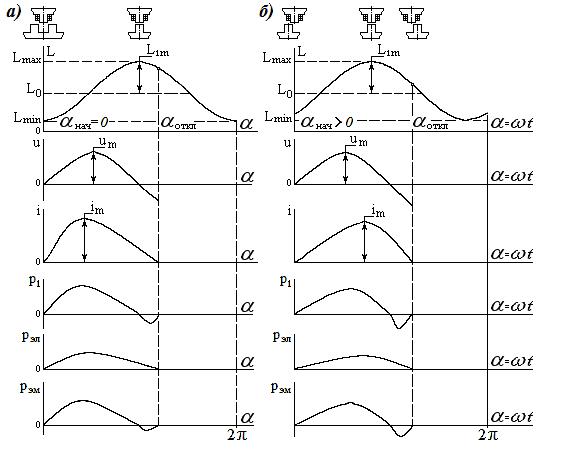
Рисунок 2 – Диаграммы изменения L(), u(), i() и мгновенных значений потребляемой  мощности р1(), электрических потерь рэл() и электромагнитной мощности рэм() для вентильно-индукторного двигателя: а) принач = 0, что соответствует максимальному моменту; б) при нач > 0, что соответствует моменту меньше максимального.

 

Выражение для фазного тока во второй обмотке i2  (рисунок 1), это тот же ряд гармонических составляющих (10) только с другими начальными фазами, так как отрицательная полуволна напряжения сдвинута на фазовый угол a = π.

Сложение двух фазных токов позволяет получить выражение для линейного тока в следующем виде:

,

(11)

где

       ikл.m – амплитуда k – ой  гармоники линейного тока;

 φkл – начальная фаза k – ой  гармоники линейного тока.

Анализ выражения (11) показывает, что постоянная составляющая и четные гармоники фазных токов замыкаются внутри схемы обмотки (при этом складываются арифметически), а нечетные гармоники (складываются с учетом начальных фаз токов обоих обмоток) и замыкаются через сеть.

Естественно, рабочей гармоникой линейного тока является основная, в то время как высшие генерируются в сеть, что является специфической особенность все силовых схем с элементами силовой электроники.

Действующее значение фазного и  линейного токов определяются с помощью выражений:

,

(12)

,

(13)

 

Потребляемая мощность из сети (например, для схемы в две звезды) будет определяться с помощью выражения

,

(14)

где  – коэффициент мощности;

       – коэффициент искажения (учитывает наличие высших гармоник в линейном токе);

      φ1u , φ1i – соответственно, начальные фазы основных гармоник напряжения и тока.

Электрические потери в обмотках фаз статора тогда будут равны

,

(15)

и пренебрегая магнитными потерями, получаем выражение для электромагнитной мощности

(16)

 

и электромагнитного момента

,

(17)

где ω1 = πn1/30 – синхронная угловая частота перемещения максимумов МДС.

«Энергетический» КПД, каждого из рассматриваемых двигателей, можно определить как

,

(18)

Представленные в графическом виде на рисунке 2 мгновенные значения фазного тока и мощностей показывают, что продолжительность его протекания (из-за наличия L0) заметно превышает полпериода. После прохождения максимума индуктивного параметра (ось полюса статора совпадает с ось полюса ротора) происходит одновременно два физических процесса:

1. Переход данной обмотки фазы в генераторный режим работы;

2. «Гашение поля» – вывод запасенной ранее катушкой обмотки фазы магнитной энергии в сеть (из-за наличия отрицательной полуволны напряжения).

При самокоммутации опасность перехода в генераторный режим состоит лишь в том, что на этом временном интервале большая часть механической энергии преобразуется и  возвращается в сеть за вычетом электрических потерь, что естественно будет снижать степень использования активных материалов.

Величина угла начала коммутации αнач для каждого из рассматриваемых в статье индукторных двигателей устанавливается в зависимости от момента нагрузки, то есть при αнач = 0, когда L(α) = Lmin электромагнитный момент будет имеет максимальное значение. Если придавать αнач приращения Δα, то величина электромагнитного момента будет уменьшаться и при αнач  =  α0 будет получено значение Рэм = 0, что соответствует "идеальному" холостому ходу. Потребляемая активная мощность Р1.0 будет покрывать только электрические потери. Это обстоятельство позволяет для рассматриваемых двигателей в статье ввести понятие угла нагрузки θ и угловой характеристики Мэм = f(θ) при изменении  αнач ≤ θ ≤ α0. Вид Мэм = f(θ), величина электромагнитного момента исключительно зависят от параметров ε (или) mL и tgφ0.

Представленная математическая модель только кажется сложной, но использование того или иного математического пакета позволяет получить не только количественную оценку, но и графическое представление происходящих электрических и электромагнитных процессов в рассматриваемых индукторных двигателях при вентильной самокоммутации. Особо следует отметить, что введение понятия угла нагрузки θ при изменяющейся форме фазного тока и его максимума имеет несколько иной физический смысл, отличный от синхронных машин классического типа.

Математическая модель удобна не только для задач анализа, но и для задач синтеза. В техническом задании на разработку того или иного типа рассматриваемого в статье индукторного двигателя обязательно указываются полезная мощность Р2н, частота вращения n2, напряжение питания и частота сети. Отсутствие требований к энергетическим показателям усложняет задачу синтеза, однако первоначальным ориентиром  на КПД и коэффициент мощности могут служить асинхронные двигатели на мощность до нескольких киловатт с 2р = 4 – 10. Ориентир на КПД  позволяет установить потери в двигателе (основная их доля в обмотке статора), тем самым без особых проблем (с учетом m2, N и возможно s) определить активное cопротивление обмотки фазы R. Дальнейшей задачей синтеза является подбор ε (или mL) и tgφ0, удовлетворяющих поставленной задаче и воплощению их в конкретную конфигурацию магнитной системы и количества витков катушек, образующих обмотку фазы. Для этой цели можно воспользоваться следующими источниками [2, 3 и 4].

 

Литература

 

1. Наний В.П. Электродвигатели с катящимся ротором и многофазным пульсирующем полем. – Харьков: ХВКИУ, 1967.

2. Алексеева М.М. Машинные генераторы повышенной частоты. – Л.: Энергия, 1967.

3. Дискретный электропривод с шаговыми двигателями / Ивоботенко Б.А. и др. Под общ. ред. М.Г. Чиликина. – М.: Энергия, 1971.

4. Кулик Ю.Д. Особенности расчета вентильно-индукторного двигателя с неуправляемой коммутацией для вентильно-индукторного привода // Актуальные проблемы энергосберегающих технологий. Труды Всероссийской научно-технич. конф. с международным участием. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006.

 

MATHEMATIC MODELS OF SWITCHED-RELUCTANCE MOTORS WITH PULSE POWER SUPPLY FROM SINUSOIDAL SOURCE

 

Kulick Y. D., Polyuschenkov I. S.

 

The article proposes a mathematical model of low-speed switched-reluctance motor with pulse power supply directly from sinusoidal electric source. Mathematical description takes account the parametric nature of winding phase circuit with introduction of two parameters: relative main component of inductance and ratio of steady inductance component with resistance of the phase winding. The proposed model of switched-reluctance motor with electromechanical and electromagnetic reduction allows to solve engineering problems in analysis and synthesis for specified motors.

Key words: concentrated phase winding, gate switching, electromechanical and electromagnetic reduction, power efficiency, load angle.  

 

Сведения об авторах:

Кулик Юрий Дмитриевич окончил Электромеханический факультет МЭИ в 1967 г. Кандидат технических наук, доцент. Защитил кандидатскую диссертацию по теме «Двигатель с гибким ротором и расщеплённой магнитной системой» в 1978 г. в МЭИ. Доцент кафедры «Электромеханические системы» филиала МЭИ в г. Смоленске.

Моб. телефон: 89107145568

Рабочий телефон: (4812) 64-17-92

 

Полющенков Игорь Сергеевич окончил Смоленский филиал МЭИ в 2008 г. Кандидат технических наук. Защитил кандидатскую диссертацию по теме «Разработка бездатчикового вентильно-индукторного электропривода с искусственной нейронной сетью» в 2013 г. в МЭИ. Старший преподаватель кафедры «Электромеханические системы» филиала МЭИ в г. Смоленске. 

Рабочий телефон: (4812) 64-17-92

Моб. телефон: 89156505419

E-mail: polyushenckov.igor@yandex.ru

 

Филиал ФГБОУ ВПО «Национальный исследовательский университет «МЭИ» в г. Смоленске

Поступила в редакцию 9.01.2014