Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 13. -
Вып. 1. - 2014. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/TITL-41.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/cont.htm
УДК 681.2-5
МНОГОФУНКЦИОНАЛЬНАЯ
СИСТЕМА ДОЗИРОВАНИЯ И РАПРЕДЕЛЕНИЯ ПОТОКОВ ЖИДКОСТИ В ТЕХНОЛОГИЧЕСКОМ ПРОЦЕССЕ
Ó 2014 г.
Делеговская Т. В., Найдёнов Е. В., Прокофьева П. А.
В работе описан процесс создания многофункциональной математической
модели, которая может быть использована для автоматического расчёта дозирования
потов жидкости в разнообразных технологических процессах.
Ключевые слова: дозирование, распределение, поток, система расчёта.
В современном высокотехнологическим мире,
с расширением функциональных возможностей систем компьютерной математики (СКМ),
разработка большинства устройств начинается с создания её математической модели.
Как правило, такой подход позволяет сэкономить значительное количество средств
на доработку выпущенных макетных изделий, а при проектировании крупных объектов
вовсе заменить реальные испытания математическим моделированием в самых сложных
состояниях.
Ещё одна черта современных СКМ – это их
гибкость. Большое количество разрабатываемых математических моделей могут быть легко
адаптированы в качестве узлов других систем и устройств, поскольку библиотеки,
в которых они содержатся не предназначены для частного случая применения.
Примером может являться модель системы дозирования потов жидкости. Сегодня эта
система выполняет важные функции в широком разнообразии устройств в различных
областях: сельском хозяйстве (система орошения, система распределения первичной
продукции), промышленности (многоуровневые системы распределения нефти и газа,
системы промышленной конденсации зданий), клеточной биологии (распределение потоков
питательных жидкостей, системы инъекции) и др. (см. рис.1).
В работе ставится задача разработать
гибкую многофункциональную систему дозирования и распределения технологического
потока (газа/жидкости), которая может быть применена для различных областей
техники. Для начала следует рассмотреть структуры функционирования таких систем
(см. рис. 2). Как правило выделяют архитектуру с прямым потоком (рис 2 А) и замкнутым
контуром (рис 2 Б). Друг от друга каждую из них отличает наличие остаточной
жидкости. На архитектуре распределения прямого потока спроектированы нефти- и
газораспределительные станции, системы литья стали, множественные распылительные
системы. В этих устройствах по ряду причин не допускается возможность получения
остатка дозируемого вещества. Так, перекачиваемый объём газа подлежит строгому
учёту, а затвердевание стали остановит технологический процесс. В системах с
замкнутым контуром частично- и неиспользованный поток возвращается в резервуар.
В большинстве случаев эти системы содержат сложный механизм субсистемы, которая
потребляет питательную жидкость. И как правило, процесс его дальнейшего
распределения предусматривает наличие остатка. Остаток питательной жидкости в
ряде случаев может быть отфильтрован. Следует заметить, что остаток может быть
образован в процессе химической реакции и содержать продукты других элементов. Ещё
одним фактором может являться низкая активность влияния среды, в которую
поступает технологический поток. Так в областях генной инженерии и
биотехнологий, клеточной биологии, фармакологии и многих других, среда может иметь
особый, нелинейный характер потребления питательной жидкости (которая выступает
в качестве исследуемого потока). В таких случаях, когда процесс потребления не
имеет устойчивой характеристики, новым требованием является постоянная регулировка
и подстройка системы дозирования.

Рисунок 1 – Система дозирования
и распределения потоков
в различных технологических процессах
Универсальная модель системы должна
оперировать любым объёмом технологического потока и производить точный расчёт
его распределения. Системы дозирования в большинстве случаев содержат управляемые
вакуумные, диафрагменные или электромагнитные клапаны, сигнал действия которых
подаёт как правило электронно-цифровая система управления (СУ). В свою очередь,
для определения момента открытия того или иного клапана, СУ имеет либо
программный алгоритм (содержащий условия открытия), либо ряд датчиков во
внешней среде: температурные, газовые, кислотные и др., либо получает сигналы
от находящейся в среде системы технического зрения. Однако, для множества простых
систем датчики и СУ могут отсутствовать (например, система орошения полей). В
этом случае оператор вручную регулирует уровень открытия каждого клапана, теряя
при этом потоки воды, вылитые впустую.
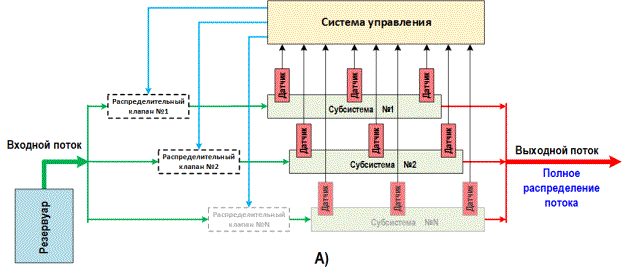
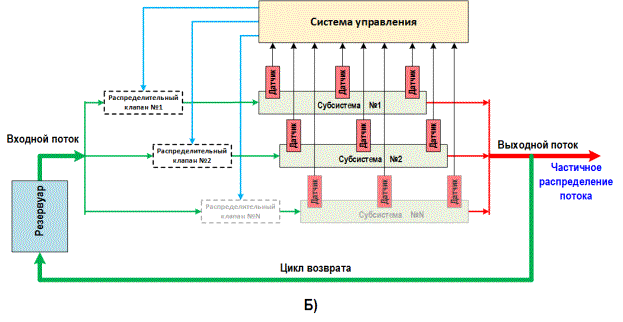
Рисунок 2 – Разновидности
архитектуры систем дозирования потоков
А) с прямым потоком; Б) с
замкнутым контуром
Используя математические выражения
постараемся сформулировать простой алгоритм, позволяющий отразить процесс
дозирования потока.
Задаём следующие базовые величины:
u – минимальный начальный процент протекания жидкости в
одной трубке (как правило, любые системы дозирования в начальный период работы
пропускают ограниченный технологический поток, величину которого можно
отрегулировать до пуска устройства);
k – число субсистем (распределительных труб, каналов,
технологических линий) на количество которых будет разделён входной поток;
n – число датчиков на одной субсистеме (существуют
мировые стандарты и правила для установки разнообразных датчиков в любых
условиях в зависимости от их типа; для систем технического зрения выполняется
инженерно-оптический расчёт наиболее удобного расположения в исследуемой
субсистеме).
Принимая входной поток как 100% (исходя
из постоянства работы насосных устройств в начальный момент времени), можем
определить максимальный объём потока V
(%), который доступен для одной субсистемы:
![]()
В случае, если входной поток изменяется
(например, при ручной регулировке оборотов насосного оборудования или его
поломке), величина нового сформированного потока будет пропорциональна значению
потока в начальный момент времени. При построении модели будем считать, что начальный
поток не изменяется.
Пусть M – общее количество датчиков для всей установки:
![]() ,
,
тогда остаток жидкости P (%) для распределения будет найден как:
![]() .
.
В ряде технологических процессов,
необходимым условием является возможность составлять определённый запас потока
жидкости. Это связано с последующей регулировкой выходного потока и повышением
долговечности ряда клапанов. В таком случае, величина P, может быть определена как:
![]() ,
,
где а – объём запасённой жидкости.
Пусть Z – объём жидкости (%), подаваемый на один датчик:
![]() ,
,
S (1,2,..,k) – число активных датчиков в субсистеме (1,2,..,k),
G (1,2,..,k) – объём выходного потока субсистемы (1,2,..,k).
Логичны утверждения:
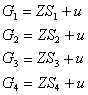
Для общего случая, для любого количества
субсистем (1,2,..,k,…), формула имеет вид:
![]()
Нераспределённый объём потока можно
выразить как:
![]() .
.
Для общего случая:
![]() .
.
На основе математических выражений была
составлена модель в СКМ Matlab&Simulink R2013b – рис. 3. Она содержит четыре распределительные
трубки-субсистемы. Проведём моделирование при ряде заданных условий. На рис. 3
отсутствует резервирование входного потока (а=0), число датчиков и субсистем
равно четырём. Для каждой субсистемы указаны разные значения активности
датчиков. Как видно из рисунка, математический рассчёт оказался верным.
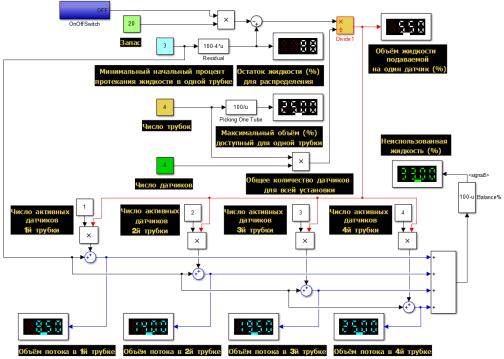
Рисунок 3 – Математическая
модель системы дозирования в СКМ Matlab&Simulink
На рис. 4 при ином
значении u, активизирован процесс резервирования.
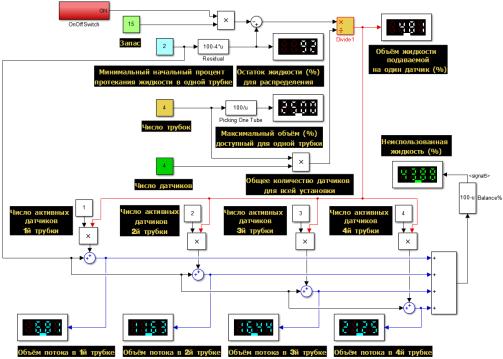
Рисунок 4 – Моделирование
при включённом резервировании
На рис. 5 отражён процесс полного
распределения входного потока. Резервирование в этом случае отключено.
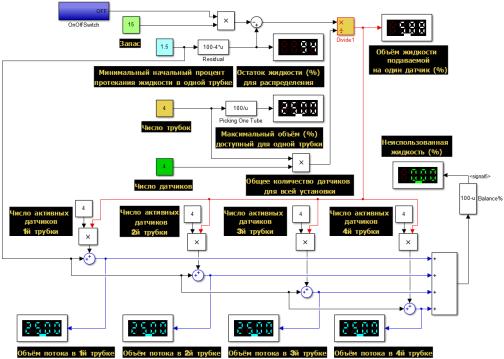
Рисунок 5 – Полное
распределение входного потока
На рис. 6 увеличено число датчиков и
запущен процесс резервирования входного потока на небольшую величину. Минимальный
процент выбран очень малым, исходя из объёма потока, приходящегося на один
датчик.
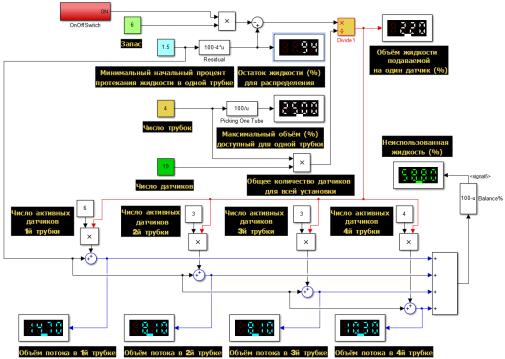
Рисунок 6 – Дозирование
потока при большом количестве активных датчиков
Для удобства использования, объединим математические
блоки в субсистему Simulink и применим возможность
задавать данные в виде меню – рис. 7,8.
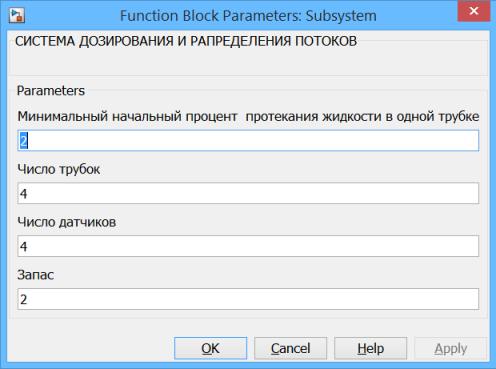
Рисунок 7 – Меню субсистемы
модели
Процесс активности срабатывания датчиков
выполним при помощи нажатия кнопок. В таком виде мы можем изменять величину
дозировки при установленных параметрах с в режиме реального времени – рис. 8.

а)

б)
Рисунок 8 – Процесс моделирования
субсистемы
Таким образом, можно утверждать, что
разработанная модель может быть применена в качестве функционального блока
моделей разнообразных устройств. Простота расчётных функций была получена путём
многократного тестирования различных распределительных систем и изучения их алгоритма
поведения. Кроме того, присутствует возможность усложнения субсистемы, для
более глубокого изучения процессов дозирования. Однако общие выполняемые
функции, заложенные в систему останутся прежними при любых внешних условиях.
MULTI-SYSTEM DOSAGE AND
STREAMS DESTREBUTION Fluids in technological processes
Delegovskaya T. V., Naydyonov E. V., Procofieva P. A.
In this paper we describe the process of creating a mathematical model
of multi-function, which can be used to automatically calculate the fluid
dispensing pots in time-ous processes.
Key words: dispensing, distribution, flow calculation
system.
Смоленский Государственный
Университет
Филиал ФГБОУВПО
«Национальный
исследовательский университет» МЭИ»
в г. Смоленске
Поступила
в редакцию 25.12.2013