Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 13. -
Вып. 1. - 2014. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/TITL-41.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/cont.htm
УДК
621.391.161
АНАЛИЗ СУЩЕСТВУЮЩИХ АЛГОРИТМОВ ОБРАБОТКИ ИЗОБРАЖЕНИЙ В СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ
Ó 2014 г.
Прокофьева П. А., Якименко Ю. И.
В статье изложен анализ существующих алгоритмов обработки изображений в
системах технического зрения с точки зрения их применимости для оценки динамики
технологического процесса.
Ключевые слова: Система технического
зрения, технологический процесс, коэффициента корреляции, алгоритм обработки
изображений.
Проведение автоматического фотомониторинга и
управление технологическим процессом возможно при помощи системы технического
зрения (СТЗ) в условиях, когда присутствие человека-оператора в производстве
ограниченно или невозможно из-за технологических условий. Для этого необходимо
снабдить СТЗ такими алгоритмами цифровой обработки изображений, которые
способны автоматически оценивать динамику технологического процесса и
вырабатывать сигналы управления для автоматики технологического процесса.
Цифровая обработка использует представление
изображения в памяти видеопроцессора в виде двумерного цифрового массива
(матрицы) 
, где 
- число строк, а
– число столбцов массива. Обработка изображения заключается
в выполнении преобразования указанной матрицы
, каждый элемент которой может принимать 
значений (уровней)
квантования. Каждое из 
значений будет
называться яркостью данного, исходного изображения в заданной точке 
(пикселе). Обычно
1<L<24.
24-битовый размер изображения способен обеспечить разрешение слабых изменений в
интенсивности излучения. Дальнейшее увеличение количества уровней квантования L не приведет
к заметному улучшению качества, а уменьшение битового размера приведет к потере
информации и возникновению ложных контуров в изображении. В результате преобразования
формируется набор числовых характеристик матрицы или новое, обработанное изображение.
Преобразование может касаться значений элементов 
или их координат
(i,j) (индексов), выполняться над матрицей в целом, группой элементов или над
каждым элементом в отдельности [3, 4, 5, 6, 8, 9].
В настоящее время существует группа алгоритмов
обработки изображений: поэлементные
преобразования, выделение контуров, обработка скользящим окном (рисунок 1). Названные
алгоритмы приводят к улучшению качества при восприятии изображения человеком
наблюдателем.
В
процессе развития теории и практики работы с изображениями под обработкой
изображений принимаются не только преобразования, приводящие к улучшению
качества видения изображения, но и те, которые приводят исходное изображение к
виду, удобному для дальнейшей их обработки с помощью машин (обеспечение
машинного (технического) зрения). В этих случаях интерес вызывают изображения
не сами по себе, а та информация, которая в них содержится. Извлечение этой
информации и составляет цель обработки видеоинформации (изображений), которое
производится автоматически, т. е. без участия оператора. Такая обработка
изображений содержит сегментацию изображений, пороговую обработку, проводимую в
интересах обнаружения объектов.
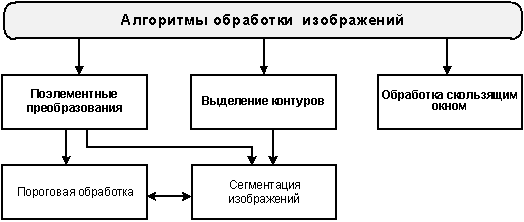
Рисунок 1 – Алгоритмы
обработки изображений
Вид цифровой обработки изображений, заключающийся в
выполнении одного и того же выбранного функционального преобразования для
каждого элемента матрицы вне зависимости от его положения и значений других
(соседних) элементов, получил название поэлементного преобразования
изображений, т. е. перевод значений каждого элемента f в
новое значение g в соответствии с выбранной функциональной
зависимостью
.
Размеры входного и выходного изображения здесь
совпадают. При
практической реализации алгоритмов поэлементного преобразования необходимо
вычислять каждое значение преобразованного элемента в соответствии с конкретным
видом функции (1.1). Алгоритмы поэлементной обработки, как правило,
используются для улучшение качества восприятия изображений
оператором-наблюдателем (рисунок 2).
Частным случаем поэлементной обработки можно считать
пороговую обработку каждого элемента изображения. Сущность алгоритма пороговой
обработки заключается в разделении элементов цифрового массива изображения на несколько непересекающихся подмножеств,
которые все вместе составляют множество элементов целого изображения. При этом
предполагается, что элементы каждого из подмножеств обладают некоторой степенью
общности, которая позволяет рассматривать их как один класс. Характер этой общности
определяется особенностями решаемой задачи. Исходя из этого полученные подмножества иногда называют классами, а
процесс обработки называют классификацией.
|
|
|
|
|
а) |
|
б) |
Рисунок 2 – Результаты использования
поэлементной обработки изображения:
а)
изображение до обработки;
б)
изображение после обработки
Результат пороговой обработки принято представлять в виде
изображения, имеющего столько же элементов, сколько их содержит исходное
изображение. В ходе пороговой обработки всем точкам результирующего
изображения, принадлежащим одному классу, присваивается одно и то же значение.
В простейшем случае получается бинарное изображение, применяемое для
информационной поддержки систем
технического зрения.
Таким образом, алгоритмы поэлементной обработки, как
правило, используются для улучшение качества восприятия изображений
оператором-наблюдателем или сформировать бинарное изображение пригодное для
использования в простых системах технического зрения.
Исследованиями психологов установлено, что в плане
зрения распознавания объектов на изображении наиболее информативными являются
не значения яркостей объектов, а характеристики их границ – контуров. Другими
словами, основная информация заключена не в яркости отдельных областей, а в их
очертаниях. Задача выделения контуров состоит в построении изображения именно
границ объектов и очертаний однородных областей. Контуром изображения
называется совокупность его пикселей, в окрестности которых наблюдается
скачкообразное изменение функции яркости.
В соответствии с алгоритмом обработки изображения
выделения контуров вычисление производится в два этапа. Сначала изображение
обрабатывается (проводится двумерная
свертка) двумя двумерными фильтрами. Импульсные характеристики этих фильтров
соответствуют «маскам» («окнам»):
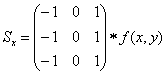и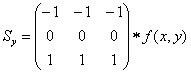 
.
На втором шаге проводится квадратурная обработка
Итогом которой является изображение с обозначенными
контурами (рисунок 3).
Таким образом, операция выделения контуров заключается
в выполнении нелинейной свертки изображения и «окна» в двух противоположных
направлениях с последующей квадратурной обработкой для получения контурного
изображения.
|
|
|
|
|
а) |
|
б) |
Рисунок 3 – Результаты
использования обработки изображения выделением контуров:
а)
изображение до обработки;
б)
изображение после обработки
Метод сегментации (препарирования) изображений заключается в приведении их к виду, далекому от естественного, но удобному для
визуальной интерпретации или дальнейшего машинного анализа. Сегментация состоит в принятии
решения о наличии объекта для каждой точки изображения. Смысл этого уровня состоит в автоматическом разбиении изображения на содержательно
интерпретируемые области. Важным в прикладном отношении значением этого уровня
обработки информации является подготовка
к процессу обнаружения (выделения) объектов (целей), различных как по своим
яркостным и геометрическим свойствам, так и по физической интерпретации [3,
4, 5, 6, 8, 9].
Математическая постановка задачи сегментации. Пусть f(x,y) – функция
яркости анализируемого изображения; X
- конечное подмножество
точек плоскости, на котором определена функция f(x,y); S = {S1,S2,…,Sk} – разбиение X
на К непустых связных подмножеств Si, i = 1,2,...,К;
LP – предикат, определенный на
множестве S и принимающий истинные значения
тогда и только тогда, когда любая пара точек из каждого подмножества Si удовлетворяет некоторому критерию однородности.
Сегментацией изображения f(x,y) по предикату
LP называется разбиение S = {S1,S2,…,Sk},
удовлетворяющее условиям:
а)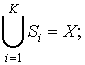 
б) 
в) 
г) 
Условие (а) означает, что каждая точка изображения должна быть отнесена
к некоторой области, (б) означает, что области
Si должны быть связными, (в) определяет вид (тип) однородности
получаемых областей, (г) выражает свойство «максимальности» областей разбиения.
Подразумевается, что разбиение S
существует и оно единственно. Предикат LP
в (б) называется предикатом однородности и его истинное или ложное значение
зависит от свойств функции f(x,y).
Предикат может быть определен как
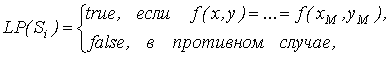
где 
m=1, 2,…, M, M – число
точек в области Si, либо как
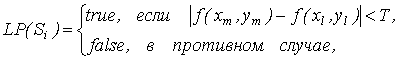
где 
– произвольные точки
из области Si;
Т – величина некоторого наперед заданного порога.
Таким образом, сегментацию можно рассматривать как оператор вида
при 
где 
–
функции, определяющие исходное и сегментированное изображения соответственно; 
- метка (имя) i-й области.
Существуют два общих подхода к решению задачи сегментации. Первый
подход основан на «разрывности» свойств точек изображения при переходе от одной
области к другой. Этот подход сводит задачу сегментации к задаче выделения
границ областей. Второй подход основан на выделении точек изображения,
однородных по своим локальным свойствам, и объединении их в область, которой
позже будет присвоено имя или смысловая метка. Первый подход называют
сегментацией посредством выделения границ областей, а второй - сегментацией посредством разметки точек области
(рисунок 1.13).
Сегментация посредством разметки точек сегмента
осуществляется при помощи поэлементных преобразований специальных видов. Так,
частным случаем сегментации является пороговая обработка, рассмотренная выше
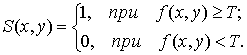
Таким образом, пороговая обработка является одним из основных подходов
к решению задачи сегментации изображений. Это объясняется ее «относительной
простотой в вычислительном аспекте, а также тем, что наиболее характерным признаком
объектов в реальных сценах является перепад яркости.
Если неравномерное освещение описывается некоторой
известной функцией, то его можно скомпенсировать на этапе предварительной
обработки с помощью методов коррекции уровней яркости. Тогда при сегментации
глобальная пороговая обработка дает удовлетворительные результаты. При
отсутствии информации о виде этой функции изображение разбивают на блоки и
выбирают свой пороговый уровень в пределах каждого блока.
Если блок содержит как объект, так и фон, то его гистограмма яркостей
будет бимодальной. Минимальное значение гистограммы на участке между модами
даст локальный порог для выделения объекта на фоне в данном фрагменте
изображения. Когда блок содержит только объект или только фон, гистограмма
унимодальна и локальный порог для фрагмента не может быть определен. В этом
случае он назначается путем интерполяции локальных порогов, найденных для
ближайших бимодальных фрагментов.
Помимо описанных ситуаций к применению методов
обработки с переменным порогом приводит задача выделения небольших по площади
объектов, разбросанных на фоне, составляющем большую часть изображения. В этом
случае точки объектов не дают заметных пиков на гистограмме яркости. Поэтому
необходимо переходить к построению гистограмм небольших фрагментов, проверять
их на бимодальность, а найденные локальные пороги интерполировать на оставшуюся
часть изображения [3, 4, 5, 6, 8, 9].
Выбор глобального порога непосредственно по
гистограмме яркостей. Введем следующие обозначения. Сегментации подвергается
изображение f(x,у); x=1,…M;
y=1,…N с динамическим
диапазоном L уровней яркости. Каждому
уровню i соответствует ni точек изображения. Общее количество точек равно n=M×N=n1+n2+...+nL. Гистограмма
яркостей рассматривается как оценка распределения вероятностей
, i=1, L; рi≥0,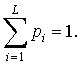 
Осуществляется сегментация на два класса точек по пороговому уровню t l0={(х,у): f(x,у) ≤ t*}
— класс точек фона; l1={(x,у)
: f(x,y)>t*} —класс
точек объекта,
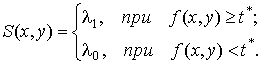
Самым распространенным методом использования гистограмм яркостей для
пороговой обработки изображений является так называемый метод мод [21, 39-41]. Метод вытекает из предположения, что изображение
содержит известное число однородных по яркости классов точек, т. е. таких
классов, распределения вероятностей яркости которых унимодальны. Кроме того,
считается, что граничные участки между замкнутыми областями занимают
сравнительно небольшую площадь изображения. Поэтому на гистограмме им должны соответствовать
межмодовые впадины, в пределах которых устанавливаются пороги сегментации (рисунок
4).
Исходя из этого изображение f(x,у) преобразуется в бинарное S(x,у). Такое преобразование осуществляется в первую очередь
для того, чтобы сократить информационную избыточность изображения, оставить в
нем только ту информацию, которая нужна для решения конкретной задачи. В
бинарном изображении должны быть сохранены необходимые детали (например, очертания изображенных
объектов) и исключены второстепенные
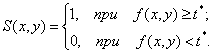
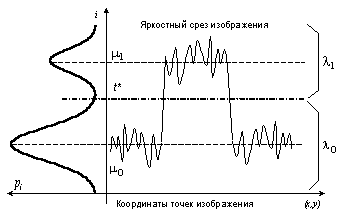
Рисунок 4 – Одномерный срез
перепада яркости и гистограмма яркостей
К сожалению, изображения реальных сцен плохо удовлетворяют выдвинутым
предположениям. Как правило, границы между областями на изображении размыты.
Поэтому модальная структура гистограммы выражена недостаточно, а уровень отдельных
мод сравним с уровнем шума на гистограмме.
Для автоматического определения порога сегментации может быть
использован итерационный алгоритм, в соответствии с которым вначале выбирается
начальная оценка порога Т, затем производится пороговая обработка
изображения с порогом Т, в результате чего образуется две группы
пикселей: G1 и G2. После
этого вычисляются средние значения яркостей m0 и m1 по областям
G1 и G2. На основе m0 и m1 определяется новое значение порога 
(рисунок 5).
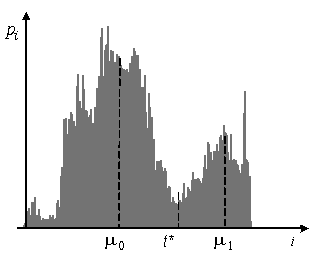
Рисунок 5 –
Полимодальная гистограмма яркостей изображения объекта и фона
Далее процесс повторяется с самого начала, но уже с новым значением
порога. После нескольких итераций, когда разница значений Т при соседних
итерациях окажется меньше наперёд заданного порога Т0,
процесс уточнения порога обрывается.
Таким образом, последовательное вычисление среднего уровня яркости всех
граничных точек с получением на каждой итерации бинарного изображения в
конечном счете даст стабильное решение, соответствующее оптимальному порогу,
выбранному в центральных точках профилей перепадов яркости. Если изображение
содержит более чем два класса однородных по яркости точек, они могут быть
выделены назначением нового пробного порога и повторением итераций до получения
стабильного решения, отличающегося от прежнего.
Практически любое изображение зашумлено, а значит, возникает проблема
борьбы с шумами. Одним из наиболее распространенных способов борьбы с шумами
является фильтрация, которая с самого начала была применена к обработке одномерных
сигналов. Не составляет исключения и борьба с шумами на зашумленных
изображениях, но с особенностями, связанными с двумерностью видеоинформации.
Указанная особенность приводит к тому, что вместо одномерного фильтра,
предназначенного для фильтрации зашумленных сигналов одной переменной (обычно
этой переменной является время), для фильтрации изображений чаще всего
применяются двумерные фильтры, представляющие собой апертуры (маски) различной
конфигурации на плоскости. Каждому элементу апертуры соответствует
(присваивается исследователем) число, в дальнейшем называемое весовым
множителем [3, 4, 5, 6, 8, 9].
Фильтрация осуществляется перемещением слева – направо (или сверху –
вниз) апертуры фильтра (маски) на один пиксель. При каждом положении апертуры
производятся однотипные операции, а именно перемножение весовых множителей с
соответствующими значениями яркостей исходного изображения и суммированием
полученных результатов. Полученное значение делится на заранее заданное число
(нормирующий множитель), которое и присваивается центральному элементу апертуры
(это и есть «выход» фильтра). Размеры апертуры берутся таким образом, чтобы
центральный элемент апертуры определялся однозначно. Наиболее распространенные
размеры апертуры 3×3 и 5×5
[3, 4, 5, 6, 8, 9].
Указанная процедура
имеет вид:
,
Соотношение 
описывает двумерную
свертку функции яркости исходного изображения 
с импульсной реакцией
некоторой двумерной
системы. Выбирая определенным образом коэффициенты маски 
, а также ее размеры, можно выполнить различные операции по
улучшению качества изображения: повышение резкости, сглаживание шумов, подчеркивание
контуров, низкочастотную или высокочастотную фильтрацию и так далее. Из
соображений простоты обычно применяются окна малых размеров 3×3 или
5×5 [3, 4, 5, 6, 8, 9].
Таким образом, рассмотренные методы обработки
изображения реализуются при помощи алгоритмов цифровой линейной и нелинейной
фильтрации. Отличительной особенностью линейной фильтрации является простой
набор операций над элементами массива изображения (умножение на число, сложение
и т. д.). В процессе нелинейной
фильтрации используется более широкий набор операций (умножение, деление,
возведение в степень, взятие модуля, определение максимума, минимума, медианы и
т. д.).
Для иллюстрации работы алгоритма линейной фильтрации изображений рассмотрим схему
искажения и фильтрации (восстановления) изображений, представленную на рисунке
6.
Таким образом, алгоритм обработки изображений скользящим окном
применяется для обозначения крупноразмерных объектов.
Широкий спектр алгоритмов
цифровой обработки изображений обработки
получены для простейших стационарных моделей объектов и способны
улучшать качество, выделять границы, обозначать крупноразмерные объекты и
получать бинарные изображения, необходимые для обеспечения технического зрения.
Итак, рассмотренные методы цифровой обработки изображений имеют
различные характеры в смысле их общности и теоретической значимости. Большая их
часть эвристическая, меньшая получена из строгих математических моделей путем
решения задач оптимизации в соответствии с определенными критериями качества.
|
|
|
|
|
а) |
|
б) |
Рисунок 6 – Результаты
использования обработки изображений скользящим окном:
а)
изображение до обработки;
б)
изображение после обработки
Цифровая обработка в условиях
нестационарного процесса излучения объектов связанной со случайным характером
протекания технологического процесса должна использовать статистический функционал обработки,
чувствительный к динамики случайного
процесса.
Литература
1.
Алпатов Б.А., Бабаян
П.В., Балашов О.Е., Степашкин А.И. Методы автоматического обнаружения и
сопровождения объектов. Обработка изображений и управление. М., Радиотехника,
2008. 176 с.
2.
Антонов А.В., Никулин М.С. Статистические модели в теории надежности. Учебное
пособие. М.: Абрис, 2012. - 389 с.
3.
Бакут П. А.,
Колмогоров Г.С., Ворновицкий И. Э. Сегментация изображений: методы пороговой
обработки. // Зарубежная радиоэлектроника. № 10, 1987. С. 6–24
4.
Гансалес Р., Вудс Р. Цифровая
обработка изображений. М., Техносфера, 2005.1012 с.
5.
Гансалес Р., Вудс Р.,
Эддинс С. Цифровая обработка изображений в среде MATLAB. М., Техносфера, 2006.
615 с.
6.
Сойфер В. А.
Методы компьютерной обработки изображений. М., ФИЗМАТЛИТ, 2003. 784 с.
7.
Тымкул В.М, Тымкул Л.В.
Оптико-электронные приборы и системы. Теория и методы энергетического расчета:
учебное пособие. Новосибирск: СГГА., 2005. 215 с.
8.
Яне Б. Цифровая
обработка изображений. М., Техносфера, 2007. 583 с.
9.
Якушенков
Ю.Г. Теория и расчёт
оптико-электронных приборов: учебник. М.: Логос, 2011. 567 с.
THE ANALYSIS OF EXISTING
ALGORITHMS OF PROCESSING OF IMAGES IN SYSTEMS OF TECHNICAL SIGHT
Prokofieva P. A.
Yakimenko Yu.I.
In article the analysis of existing algorithms of
processing of images in systems of technical sight from the point of view of
their applicability for an assessment of dynamics of technological process is
stated.
Key words: System of technical sight,
technological process, correlation coefficient, algorithm of processing of
images.
Филиал ФГБОУВПО
«Национальный
исследовательский университет» МЭИ»
в г. Смоленске