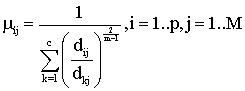Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 13. -
Вып. 2. - 2014. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/TITL-42.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/cont.htm
УДК 519.86
ЛОКАЛЬНО-АППРОКСИМАЦИОННЫЕ АЛГОРИТМЫ КЛАССИФИКАЦИИ ТРАЕКТОРИЙ
Ó 2014 г. Гимаров В. А., Гимаров
В. В., Дли М. И.
В настоящее время анализ динамических рядов является
актуальной проблемой для многих предметных областей, например, таких как медицинские
исследования, анализ социально-экономических процессов, диагностика состояния
сложных технических систем и других. Алгоритмы анализа таких данных
разнообразны и построены на структурном и поточечном сопоставлении траекторий,
отражающих динамические ряды. В статье изложены предложения
автора о применении процедур локальной аппроксимации для решения задачи
классификации траекторий на основе критериев точечного сходства. Суть
представленного метода заключается в представлении рядов в виде матричных
наборов данных и применении алгоритма нечетких c-средних для их дальнейшей
кластеризации.
Ключевые слова:
динамические ряды, локальная аппроксимация, нечеткая логика, алгоритм нечетких c-средних, кластеризация, центры кластеров.
На сегодняшний день в основе
применяемых методов анализа данных лежит представление исследуемых объектов в
виде вектора значений определенного набора признаков, которые описывают
состояние объекта в данный момент, не учитывая при этом временной динамики
изменения значений. Такой подход является статическим и плохо применим для решения
большинства практических задач, в которых анализ динамики изменения признаков является
более значимым, чем отдельный временной срез значений параметров [7]. В связи с этим проведение анализа данных должно основываться
на исследовании траекторий изменения значений факторов, описывающих состояние
исследуемого объекта.
Основы
классификационного анализа динамических данных рассмотрены в работах отечественных
и зарубежных ученых [1,2].
В работе [2] в качестве показателя классификации используется средняя
близость точек в классе. Однако при использовании многомерной информации,
изменяющейся во времени, использование данных алгоритмов классификации невозможно,
так как данные невозможно сопоставить. В работе [2] проанализирована возможность выполнения динамического
классификационного анализа на основе критерия качества классификации в виде
обобщенного среднего.
В работе [1] классификация траекторий основана на применении аппарата
нечеткой логики и предполагает выделение двух типов схожести траекторий:
- структурное сходство: чем
больше две различные траектории имеют общего в форме, динамике изменения,
характеристиках, тем больше сходства между этими двумя траекториями;
- точечное сходство: чем
меньше расстояние между точками двух траекторий, тем большее сходство
наблюдается между ними.
Структурное сравнение, прежде всего, используется в ситуациях, когда необходимо осуществить классификацию фрагмента траектории с высокой точностью. Поточечное сходство предопределяет близость траекторий в пространстве. В этом случае поведение траекторий не является единственным фактором, и некоторые различия по форме допустимы, так как траектории пространственно близки. В отличие от структурного сходства, расчет точечного не требует использования характеристик траекторий и основывается непосредственно на их значениях.
Как представляется, для решения задачи классификации
траекторий с использованием критериев точечного сходства, может быть применен
алгоритм c-means и методы локальной аппроксимации,
основные положения которых изложены в работах [5,6]. Применение процедур локальной аппроксимации для
решения задачи классификации траекторий включает следующие этапы [4]:
1) Построение локально-аппроксимационных моделей,
описывающих траектории изменения состояний системы, которые представляют собой наборы
строковых данных вида 
.
Для получения таких данных применяется процедура [3]:
1. Проведение эксперимента с фиксацией значений 
и создание исходной
матрицы U с количеством строк, большим М.
2. Ввод нового значения 
. Расчет прогнозируемой величины 
по формуле:
где
F – матрица размера 
, строками которой являются 
3. Анализ истинности
неравенства:
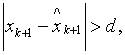
где
d – некоторая заданная константа, предопределяющая
показатель точности модели.
Если неравенство верно, в матрицу U дополнительно
включается строка 
. В противном случае матрица U не изменяется.
4. Анализ выполнения условий прерывания работы
алгоритма (общее число значений 
, используемых для формирования матрицы U может быть как фиксированным или переменным);
например, условием останова процесса обучения может быть невыполнение
неравенства, приведенного на этапе 3 
раз подряд. При его неисполнении
осуществляется переход к этапу 2, в противном случае – переход к пункту 4.
Необходимо отметить, что нескольких уточняющих
итераций (по выбору параметров 
) достаточно для создания матрицы U умеренной величины, при которой прогностические показатели
алгоритма отвечают допустимым.
В результате, любая из анализируемых траекторий изменения
состояний системы представляется в виде набора данных (матрицы) U. Для проведения кластеризации траекторий на определенное
(заданное заранее) количество подмножеств (кластеров), в каждом из которых анализируемые
объекты схожи между собой, целесообразно применять метод нечетких c-средних.
2) На каждом этапе стандартного алгоритма
нечетких С-средних в соответствии со следующей формулой рассчитывается значение
функции принадлежности объекта i к классу j:
|
|
|
где
Хi - i-ый
объект (траектория), Vj и Vk - центры кластеров j и k, с - число кластеров, m - степень размытости кластеров.
Выражение d(X,V) используется
для представления меры близости между двумя векторами. Для определения данной
меры используется предложенная автором методика.
На первом этапе для каждой пары матриц U, описывающих анализируемые траектории динамики изменения
состояния системы, проводится следующая процедура.
Проводится поиск строк в наборах данных U, максимально близких друг к другу по значениям. Так, в
локальной модели 
поиск близких строк
будет выполняться в соответствии с выражением [6]:
Для найденных пар строк наборов данных проводится
построение локальных моделей 
и рассчитываются
величины 
. Таким образом, мера близости двух траекторий может быть
определена с помощью выражения:
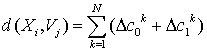
С помощью данной меры сходства между функциями
классический алгоритм нечетких С-средних можно использовать для классификации
динамических объектов. При этом расчет центров кластеров bi будет
осуществляться по формуле:
|
|
|
,
Перерасчет значений функций принадлежности:
|
|
|
Таким образом, с помощью описанного алгоритма траектории динамики состояния системы объединяются в отдельные классы, что позволяет повысить эффективность принятия управленческих решений.
Литература
1. Angstenberger L.
Dynamic Fuzzy Pattern Recognition with Applications to Finance and Engineering.
Boston: Kluwer Academic Publishers, 2001.
LOCAL APPROXIMATION CLASSIFICATION ALGORITHM PATHS
Gimarov V. A., Gimarov V. V., Dli M. I.
Currently, the analysis of dynamic rows is an
urgent problem for many areas , such as medical research , analysis of socio-
economic processes , diagnostics of complex technical systems , and others.
Algorithms for analyzing such data are varied and are built on structural and pointwise
comparison trajectories reflecting the dynamic rows . The article describes the
author's proposals on the use of local approximation procedures for solving the
problem of trajectory classification based on the criteria of point similarity.
The essence of the method is presented in the rows representation in the form
of matrix data sets and application of the algorithm of fuzzy c- means for
their further clustering.
Key words: time series, local approximation, fuzzy logic
algorithm fuzzy c-means, clustering, cluster centers.
Работа поддержана грантом РФФИ
№12-01-00266-а
Информация об авторах:
Гимаров Владимир Александрович, доктор технических
наук, профессор, филиал ФГБОУ ВПО «Национальная исследовательский университет
«МЭИ» в г. Смоленске, профессор кафедры менеджмента и информационных
технологий в экономике
Гимаров Владимир Владимирович, кандидат
экономических наук, филиал ФГБОУ ВПО «Национальная исследовательский
университет «МЭИ» в г. Смоленске, доцент кафедры менеджмента и
информационных технологий в экономике
Дли Максим Иосифович, доктор технических наук,
профессор, филиал ФГБОУ ВПО «Национальная исследовательский университет «МЭИ» в
г. Смоленске, заведующий кафедрой менеджмента и информационных технологий
в экономике
Филиал ФГБОУВПО «Национальный
исследовательский университет» МЭИ» в г. Смоленске
Поступила в редакцию 27.04.2014.
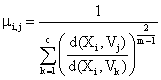
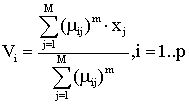