Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 13. -
Вып. 2. - 2014. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/TITL-42.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/cont.htm
Решение шестой проблемы тысячелетия
Ó 2014 г. Тукембаев Ч.
А.
Аналитическое решение уравнений Навье-Стокса для вязкой несжимаемой
жидкости является шестой проблемой тысячелетия. Предлагается решение шестой
проблемы тысячелетия, которое найдено профессором кафедры математического
анализа КГНУ им. Ж. Баласагына, доктором физико-математических наук Т. Д. Омуровым.
Его аналитическое решение опубликовал англоязычный научный журнал American
Journal of Fluid Dynamics
Ключевые слова: уравнения Навье-Стокса.
Аналитическое решение уравнений Навье-Стокса для вязкой несжимаемой жидкости является шестой проблемой тысячелетия [1]. Уравнения предложены французским ученым Навье в 1827 г. и окончательно сформулированы английским математиком Стоксом в 1845 г. Они имеют важное прикладное значение в деятельности человека по сравнению с иными проблемами тысячелетия, так как на их основе выполняются расчеты аэро- и гидродинамики, прогноза погоды и климата и т.д. Трудность решения уравнений Навье-Стокса вызвана их нелинейностью и усугублена необходимостью найти скорость и давление в зависимости от любых значений вязкости, как параметра, фактора в пространственной (3D) задаче.
В 1984 году камнем преткновения на пути к аналитическому решению
уравнений Навье-Стокса стал критерий Като-Мажды [2], возникший для 3D-уравнений
Эйлера идеальной жидкости (предложены Эйлером в 1755 г.). Уравнения Эйлера
получаются из уравнений Навье-Стокса, когда вязкость равна нулю, т.е. уравнения
Навье-Стокса более общие, чем уравнения Эйлера. Тем самым, критерий пополнил и
без того длинный ряд причин, из-за которых решение уравнений Навье-Стокса поднялось
до уровня проблемы тысячелетия (миллениум).
В этой связи ознакомим читателя с решением шестой проблемы тысячелетия,
которое найдено профессором кафедры математического анализа КГНУ им. Ж.
Баласагына, доктором физико-математических наук Т.Д. Омуровым, так как его аналитическое
решение опубликовал англоязычный научный журнал American Journal of Fluid Dynamics
[3], согласно правилам Математического Института Клея к публикациям [1].
Рассмотрим задачу Навье-Стокса в виде
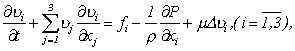 (1)
(1)
![]() (2)
(2)
![]()
![]() (3)
(3)
где
n=(u1, u2, u3) – компоненты вектора
скорости, f=(f1, f2, f3) – внешней силы, µ>0 – кинематическая вязкость, r – плотность,
D – оператор Лапласа, а уравнение
(2) – уравнение неразрывности. Скорость n и
давление P – это искомые функции нелинейной задачи (1)-(3).

Суть работы [3] в том, что разработанные Омуровым преобразования приводят к линеаризации уравнений Навье-Стокса в интегральную форму без привлечения любых надуманных условий для решения задачи (1)-(3). Тогда решение интегральных уравнений адекватно решению исходной задачи (1)-(3). Поэтому получаемое аналитическое решение регулярно относительно фактора вязкости, а потому математические значения переменных отвечают их физическому смыслу, согласно требованиям Института Клея.
Как известно, при использовании весовых пространств многие проблемы
теоретической и математической физики поддаются решению. В 2013 г. Омуров представил
в статье [4] метод и с его помощью нашел аналитическое решение задачи Навье-Стокса
в весовом пространстве, в котором по пространственным координатам допускается
гладкость 3-го порядка. Это дало возможность открыть в работе [3] новый класс
подходящих решений, построенных на основе леммы вложения К. Фридрихса [5] в весовом
пространстве типа Соболева.
Напомним, что Институт Клея предложил решить один из трех вариантов
задачи для уравнений Навье-Стокса, что было сделано, как сказано, в статье [4].
Однако Омуров обобщил полученный им в [4] результат для любых значений вязкости
в неограниченной области в обоих пространствах, так как именно этот вариант,
согласно требованиям Института Клея [1], является более предпочтительным по
сравнению с иными вариантами. После чего, решение задачи Навье-Стокса для вязкой
несжимаемой жидкости пришлось опубликовать в статье [3], как решение шестой
проблемы тысячелетия.
Успех решения зависит от изобретательности подбора нового пространства,
в котором задача разрешима, поэтому, получив решение общего варианта, нетрудно
найти решение других вариантов. Однако, подбор пространства протекает вкупе с
кропотливым поиском решения, где надо крепко поломать голову, чтобы появился
проблеск в конце туннеля. Поэтому указанные пространства, разработанные
специально для решения уравнений Навье-Стокса, открыли новую главу в
математике. Многие нерешенные задачи гидродинамики вместе с шестой проблемой
тысячелетия не устояли перед методами Омурова и приведены в работе [3] для
демонстрации преимуществ его метода.
Так вот, Омуров не ограничился формулировкой критерия Като-Мажды для
уравнений Эйлера, а распространил его на уравнения Навье-Стокса. Решение шестой
проблемы тысячелетия позволило рассматривать ее в работе [3], как принцип продолжения
сильных решений, связанных с требованиями критерия Като-Мажды, но уже для 3D-уравнений
Навье-Стокса вязкой несжимаемой жидкости. Проще говоря, когда найдено аналитическое
решение уравнений Навье-Стокса для любых µ,
то автоматически доказывается критерий Като-Мажды для уравнений Эйлера, поскольку
в них значение вязкости µ=0 отвечает
уравнению Эйлера для идеальной жидкости.
Важным приложением решения Омурова явилось исследование течений с очень
малой вязкостью в интервале 0<µ<1.
В таких вязких жидкостях сила трения весьма мала по сравнению с силами инерции,
поэтому число Рейнольдса велико: Re≥2300. Это число носит имя английского
физика Рейнольдса. Оказалось, что и в этом случае аналитические методы [3] дают
решение проблемы Навье-Стокса, чем позволяют перейти к пониманию турбулентности,
изучение которой было начато Рейнольдсом еще в 1876 г.
Помимо всего, полученные Омуровым результаты модифицированы для течения
со средней вязкостью [6], когда 0<µ=µ0=const<+¥, т.е. для уравнений
Навье-Стокса, в которых сохранятся все инерционные члены. В этом значимость результатов
работы [3], так как решение уравнений Навье-Стокса для несжимаемой жидкости со
средней вязкостью послужило лакмусовой бумажкой проверки правильности метода
Омурова и еще раз подтвердило ценность его метода. Поэтому многие до сих пор нерешенные
задачи гидродинамики ждут применения метода Омурова.
Итак, разработанные в статье [3] методы решения уравнений Навье-Стокса приводят
задачу (1)-(3) к эквивалентным линейным уравнениям типа теплопроводности с
условием Коши в классе ограниченных функций с достаточно гладкими начальными
условиями при t=0. Именно в таком
классе существует единственное условно-гладкое решение задачи Навье-Стокса в обоих
пространствах. Таким образом, решение задачи Навье-Стокса, полученное Омуровым
для вязкой несжимаемой жидкости, как главный результат работы [3], представляется
в Институт Клея для принятия решения о судьбе шестой проблемы тысячелетия [1].
ЛИТЕРАТУРА
1. Navier-Stokes Existence and Smoothness Problem // The Millennium Problems,
stated in 2000 by Clay Mathematics Institute.
2. Beale, J.T., Kato, T., Majda, A. (1984). Remarks
on the breakdown of smooth solutions for the 3-D Euler equations, Comm. Math.
Phys. 94 (1), pp. 61-66.
3. Omurov, T.D. (2014). The Methods of a Problem Decision Navier-Stokes
for the Incompressible Fluid with Viscosity // American J. of Fluid
Dynamics, Vol. 4, No 1, pp. 16-48 http://article.sapub.org/10.5923.j.ajfd.20140401.03.html
4. Omurov, T.D. (2013). Nonstationary
Navier-Stokes Problem for Incompressible Fluid with Viscosity // American J. Math. & Statistics, Vol. 3, No
6, pp. 349-356 http://article.sapub.org/10.5923.j.ajms.20130306.08.html
5. Hörmander,
L. (1985). The Analysis of Linear Partial Differential Operators III: Pseudo –
Differential Operators. - Springer-Verlag, Berlin Heidelberg New York Tokyo,
696 p.
6. Schlichting’s, H. (1974). Boundary-Layer Theory. Moscow: Science, 712 p.
Бешкек
Поступила в редакцию 18.06.2014