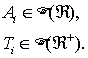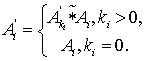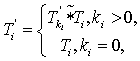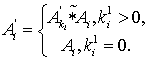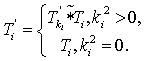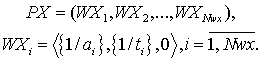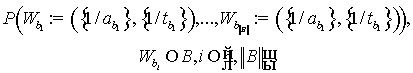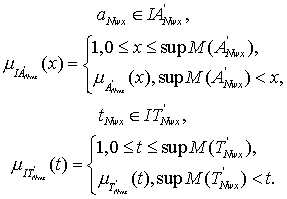Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 13. -

Вып. 2. - 2014. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/TITL-42.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/cont.htm

УДК.004.89

Способ прогнозирования временного ряда на основе идентификации нечеткого прецедента

Ó 2014 г. Зернов М. М., Курдаков К. А.

(zernov-2.doc)

В статье рассмотрены предпосылки анализа временных рядов на основе нечёткого представления сценариев их типового развития. Предложена модель представления динамики временного ряда в виде нечёткого прецедента – последовательности волн с нечеткой амплитудой и длительностью. Разработан способ идентификации прецедента относительно обработанного ряда – чёткого прецедента, а также способ прогнозирования его дальнейшего поведения. Данный способ позволяет определить продолжительную динамику временного ряда с учетом запаса до конца фазы квазилинейного изменения участка ряда. Предложенные способы позволяют анализировать временной ряд на основе качественно заданного описания сценария развития (прецедента), учитывать неопределённость в реализации такого сценария, позволяют перейти к программной реализации средств анализа на основе экспертных знаний о возможных структурах в динамике временного ряда.

Ключевые слова: анализ временных рядов, нечёткий прецедент, нечёткий сценарий.

Введение

В ряде предметных областей, связанных с анализом временных рядов, существует принципиальная возможность обоснования принимаемых решений на относительно дальнюю перспективу, исходя из знаний о типовом развитии ряда. Тогда как большинство известных классических методов анализа работают на небольшой глубине прогноза. Однако, задача распознавания подобных сценариев, с которой успешно справляются эксперты, встречает ряд проблем при попытке автоматизации. В частности, проблемой неопределённости при реализации сценария, который не повторяется в точности, хоть и следует общей структуре.

Нечеткие темпоральные модели [1], развивающие идеи гранулярных вычислений [2], являются наиболее близкими аналогами для предлагаемого подхода. Они оперируют укрупненными нечетко-темпоральными признаками временных рядов и позволяют на основе внутренней динамики процесса, характеризующей его «глубинную» предысторию, прогнозировать поведение временного ряда на относительно длительный период времени «по-крупному» путем предсказания тенденций в виде темпоральных структур гранулированных признаков, аппроксимирующих временной ряд.

Однако, они не позволяют оперировать каждым из правил в отдельности, сводя все результаты в усреднённый логический вывод. Другим недостатком подобной модели является обязательное разделение нечёткого сценария на предпосылку и заключение (описывающее лишь один этап системной динамики), тогда как было бы полезно иметь возможность уже на ранних стадиях спрогнозировать несколько этапов развития ряда. Отсутствие инвариантности к масштабу, как по амплитуде сигнала, так и по времени, также является существенным недостатком данной модели.

Таким образом, задача разработки математического аппарата, позволяющего гибко описать возможные сценарии развития временного ряда, является актуальной.

1. Модель нечеткого прецедента

Предлагается модель представления динамики временного ряда, отличающаяся рассмотрением относительного нечёткого приращения сигнала за нечёткое время, позволяющая сопоставлять сходные по структуре, но различные по временным характеристикам и/или масштабу отрезки временных рядов. Предлагаемая модель обобщает предложенную в [3] модель для идентификации реализаций паттерна Эллиотта.

Модель представляет собой нечёткий прецедент P – сценарий развития, образованный последовательностью нечётких волн/монотонных отрезков/стадий:

где W_i, iÎ[1,Nw] - отдельная нечёткая волна/стадия, которая представляет собой тройку:

,

где k_iÎ[0,i-1] – номер волны, базовой для рассматриваемой, A_i – нечёткая относительная амплитуда волны, T_i – нечёткая продолжительность волны.

Значения A_i и T_i представляют собой нечёткие множества на действительной оси и положительной полуоси соответственно:

Практически без потери общности, можем считать A_i и T_i нечёткими числами, т.е. нечёткими множествами на непрерывном действительном базовом множестве, обладающими свойствами выпуклости, компактности носителя и полунепрерывной сверху функцией принадлежности.

Волна описывает монотонное изменение амплитуды сигнала за указанное нечёткое время. Наличие локальных экстремумов в течение указанного периода полностью не исключается, но их локальность/область действия не должна превышать некоторой чувствительности. Нечёткая амплитуда является псевдолинейным приращением указанным относительно амплитуды некоторой базовой волны. Иначе говоря, чтобы рассчитать абсолютную амплитуду волны W_i – , необходимо абсолютную величину базовой волны умножить на величину A_i:

,

где операция – расширенная нечёткая операция умножения нечётких множеств.

Если допустить, что величины и удовлетворяют ограничениям, накладываемым определением нечёткого числа, операция может быть реализована на основе математического аппарата нечётких чисел более эффективно, нежели в общем случае.

Тем не менее, для практических задач, ограничение выпуклости наможет оказаться слишком строгим.

Поскольку абсолютная амплитуда волны рассчитывается через абсолютную амплитуду базовой волны, в прецеденте должны присутствовать такие волны W_i, для которых базовой волны нет, а относительная и абсолютная амплитуды совпадают. Для таких волн k_i принимают равным 0, именно они задают базу для рекурсивного определения абсолютной амплитуды произвольной волны прецедента:

,

(1)

Каждую такую волну, для которой k_i= 0 будем называть основной.

Аналогичные соотношения вводятся и для нечёткой продолжительности T_i:

(2)

где, – абсолютное значение нечёткой продолжительности волны W_i.

В некоторых, особо сложных случаях, нечёткая амплитуда и нечёткая продолжительность могут базироваться на разных волнах, а величина k_i представлять собой двумерный вектор:

,

где –номера базовых волн для амплитуды и продолжительности соответственно.

Тогда выражения (1-2) переписываются в виде:

,

В дальнейшем, если не оговорено иное, будем считать k_i скалярным значением, общим для амплитуды и продолжительности.

Заметим, что фактический масштаб прецедента задают основные волны. В общем случае, для многократного использования прецедента их можно считать переменными величинами, получающими означивание в процессе его применения. Неозначенное (нормированное) значение для нечёткой компоненты волны будем обозначать символом e, означающим чёткое множество вида:

Тогда такая основная волна W_i имеет вид:

При подстановке в основную волну W_i ненормированного значения абсолютной амплитуды и/или продолжительности из прецедента P получаем прецедент . Если более одной из основных волн получает означивание, значения для подстановки перечисляются через запятую, например:

2. Способ идентификации нечеткого прецедента относительно обработанного временного ряда

Предварительно обработаем фрагмент временного ряда X, с целью выделить монотонные участки или участки с примерно постоянной производной. Обработанный временной ряд тогда можно представить как означенный прецедент, составленный из чётких волн:

Прецедент P получает означивание только в том случае, если в прецеденте PX присутствует волна с номером, превышающим номер основной волны из P (волну с номером Nwx считаем незавершённой):

Результат означивания тогда можно представить в виде:

В результате, чёткий прецедент PX соответствует нечёткому прецеденту P, если каждая его волна, кроме последней, соответствует волне с тем же номером нечёткого прецедента по величине амплитуды и продолжительности. Последняя волна при этом соответствует волне нечёткого прецедента с тем же номером в смысле попадания амплитуды и продолжительности незавершённой волны в нечёткие интервалы от нуля до абсолютной амплитуды и абсолютной продолжительности волны с номером Nwx:

Тогда степень соответствия рассматриваемого фрагмента временного ряда X прецеденту P в целом –R(P, X) определяется как:

Крайняя сработавшая волна в прецеденте в данном случае –волна с номером Nwx.

3. Способ прогнозирования поведения временного ряда

В реальной ситуации при идентификации прецедента относительно обработанного ряда возможен случай, когда подходят сразу несколько прецедентов, различных как по числу волн, так и по значениям этих волн. Прецедент P считаем сработавшим, если степень его соответствия представленному для анализа фрагменту временного ряда R(P, X) превышает порог срабатывания: R(P, X)≥α.

Пусть, например, сработали прецеденты:

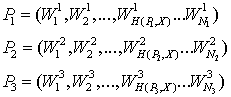
При прогнозировании будущих значений временного ряда необходимо определить, сколько времени еще будет продолжаться крайняя волна с номером Nwx, тем самым образом, установив ее запас до конца фазы.

Для этого в первую очередь необходимо перейти к четким значениям амплитуды и времени для сравнения волн между собой и дальнейшего прогноза.

Пусть – функция дефазификации. Тогда для любой волны можем найти дефазифицированные значения амплитуды и продолжительности:

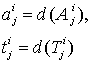
С целью повышения надежности при последующем принятии решения, в качестве d можно принять левую границу достаточно высокого α-уровня нечеткого числа.

Рассмотрим крайние волны среди сработавших прецедентов, т.е.

Исходя из пессимистической стратегии, из сработавших прецедентов выбираем тот, для которого прогноз на текущую фазу самый короткий. Т.е. прецедент P_i , для которого значение будет минимально и оставляется для дальнейшей работы.

Но может возникнуть случай, когда, например,

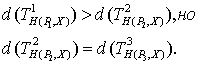
В этом случае логично взять тот прецедент, в котором сработало большее число волн. Если же и число сработавших волн совпало, выбираем прецедент с наименьшей амплитудой текущей волны. Выбранный прецедент обозначим как:

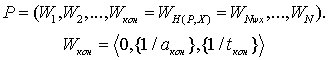
После нахождения подходящего прецедента расчет оценок запаса до конца волны по амплитуде A и продолжительности будет осуществляться следующим образом:

T = t_кон – t_x,

A = a_кон – a_x,

где t_x и a_x – продолжительность и амплитуда волны WX_Nwx чёткого прецедента (обработанного фрагмента ряда).

А непосредственно прогнозируемые значения на конец текущей фазы составят:

x_прогн = x₀ + a_кон на момент времени t_прогн = t₀ + t_кон ,

где x₀ и t₀ – координаты начала волны WX_Nwx чёткого прецедента.

Заключение

Предложенные способы позволяют анализировать временной ряд на основе качественно заданного описания сценария развития (прецедента), учитывать неопределённость в реализации такого сценария, позволяют перейти к программной реализации средств анализа на основе экспертных знаний о возможных структурах в динамике временного ряда. Указанные возможности создают основу для автоматизации поддержки принятия решений на основе экспертных знаний о типовых сценариях развития системной динамики.

литература

1. Ковалев С.М. Модели представления и поиска нечетких темпоральных знаний в базах временных рядов // Труды XI Национальной конференции по искусственному интеллекту с международным участием. – Дубна, 2008.

2. Zadeh L.A. From Сomputing with Numbers to Computing with Words - From Manipulation of Measurements to Manipulation of Perceptions// IEEE Transactions on Circuits and Systems. – 1999. – Vol.45. – P.105- 119.

3. Зернов М.М., Чуль А.Д. Модель нечёткого прецедента для идентификации реализаций паттерна волновой теории Эллиотта // Известия СмолГУ. – Смоленск: Издательство СмолГУ, 2014. №2 (26).

Method of Time Series Prediction, Based on Fuzzy Precedent Identification

Zernov M. M., Kurdakov K. A.

Prerequisites of time series prediction based on fuzzy presentation of its typical dynamics sceneries are considered in this article. Model of fuzzy precedent, representing time series dynamics as a sequence of waves with fuzzy amplitude and duration is offered. Method of precedent identification comparatively to filtered time series (explicit precedent) and method of time series further behavior are developed. The latter method allow detecting prolonged dynamics of time series, taking into account reserve up to end of phase of its quasi linear dynamics. Offered methods allow time series analyzing, basing on qualitative defined description of its dynamics scenario (precedent), and taking into account uncertainty of scenario realization. The methods allow implementing software tools for time series analysis, using expert knowledge about structures in time series dynamics.

Key words: time series analysis, fuzzy precedent, fuzzy scenario.

Зернов Михаил Михайлович – к.т.н., филиал ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске,

Курдаков Кирилл Андреевич – магистрант филиала ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске.

Кафедра вычислительной техники

Филиал ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске

Поступила в редакцию 30.05.2014.