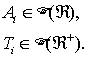Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 13. -

Вып. 2. - 2014. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/TITL-42.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-42-html/cont.htm

УДК.004.89

Способ поддержки принятия решения на основе совместного применения модели нечеткого прецедента и модели вида “ситуация-действие”

Ó 2014 г. Зернов М. М., Курдаков К. А.

(zernov.doc)

В статье предложены комплексная модель и способ поддержки принятия решения по результатам анализа временного ряда, отличающиеся совместным применением модели нечеткого прецедента и модели вида “ситуация-действие”. Решение принимается на основании прогноза величины и продолжительности квазилинейного изменения временного ряда в направлении текущей тенденции. Источником прогноза является база нечетких прецедентов (типовых сценариев динамики развития временного ряда). Рассчитанные прогнозные значения включаются в состав ситуационных признаков модели вида “ситуация-действие”, а также участвуют в формировании параметров управляющих действий. Предложенные модель и способ рассматриваются относительно задачи принятия решения о покупке/продаже на финансовом рынке.

Ключевые слова: анализ временных рядов, нечёткий прецедент, нечёткий сценарий, поддержка принятия решений, ситуационные модели.

1. Понятие нечеткого прецедента

Для многих задач, связанных с анализом временных рядов, характерен поиск часто повторяющихся устоявшихся шаблонов в этих временных рядах, что позволяет предсказывать развитие обстановки на относительно высокую глубину. Такие шаблоны называются прецедентами.

Нечеткий прецедент представляет собой последовательность волн. Каждая волна характеризует изменение амплитуды сигнала за указанное время. Волна может быть выделена на основании разницы между соседними локальными минимумами и максимумами сигнала с учетом возможного шума. Понятие прецедента на практике следует понимать как последовательность состояний, имевших место в прошлом.

Нечёткий прецедент P – сценарий развития временного ряда, образованный последовательностью нечётких волн/монотонных отрезков/стадий:

где W_i, iÎ[1,Nw] - отдельная нечёткая волна/стадия, которая представляет собой тройку:

,

где k_iÎ[0,i-1] – номер волны, базовой для рассматриваемой, A_i – нечёткая относительная амплитуда волны, T_i – нечёткая продолжительность волны.

Значения A_i и T_i представляют собой нечёткие множества на действительной оси и положительной полуоси соответственно:

В дальнейшем, при означивании прецедента, значения амплитуды и продолжительности масштабируются на основе соответствующих параметров базовой волны.

2. Модель поддержки принятия решений на основе сценариев развития временных рядов

В качестве примера выберем задачу анализа экономических временных рядов. В настоящее время широко распространены торговые площадки на финансовых рынках. Там пользователи практически непрерывно сталкиваются с вопросом о покупке или продаже валюты/ценных бумаг, т.е. принимается решение относительно направления сделки и уровня ордеров. При этом имеются устойчивые, повторяющиеся сценарии развития временного ряда, формализуемые посредством нечётких прецедентов [1].

В результате анализа рассматриваемого участка временного ряда относительно базы нечетких прецедентов может быть получено 2 варианта прогноза:

1) На основе имеющейся базы прецедентов невозможно предсказать поведение ряда.

2) Определен нечеткий прецедент, под описание которого наилучшим образом (в смысле выбранной системы предпочтений) подходит анализируемый фрагмент ряда.

Во втором случае имеется прогноз запаса по продолжительности T и величине A продолжения развития ряда в соответствии с текущим трендом.

Рассмотрим предлагаемую комплексную модель поддержки принятия решения, учитывающую указанные результаты прогноза (см. рисунок 1).

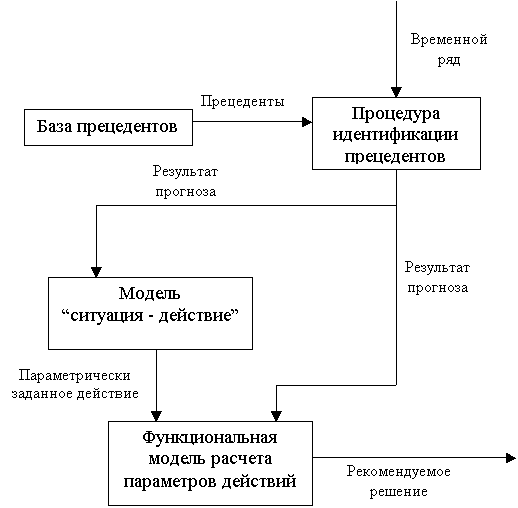
Рисунок 1 – Структура модели поддержки принятия решения

Основными компонентами модели являются:

- база прецедентов;

- процедура их идентификации;

- модель “ситуация-действие” [2];

- функциональная модель расчета параметров действий.

При выполнении процедуры идентификации прецедентов изначально выбирается, нужно ли подвергнуть ряд фильтрации или нет. Затем можно ввести требования к самим прецедентам, например, число совпавших волн, ограничения по числу самих прецедентов и т.п.

При принятии решения прогноз составляется по крайней волне ряда, которая считается незавершенной. Работа ведется именно с ней, т.к. при работе с моделью “ситуация-действие”, которая не предназначается для принятия решения более чем на один этап управления, нет необходимости в прогнозе временного ряда далее, чем до конца данной волны.

Обозначим за Y = {y₁, y₂,… , y_N} – множество ситуационных признаков, на основе которых принимается решение. Считаем, что среди них есть признаки, отвечающие за направление изменения ряда n, величину запаса движения в данном направлении по амплитуде A, и по времени T. Каждый признак представляет собой нечёткую лингвистическую переменную.

Применяемые действия по ситуациям имеют свои параметры. Данные параметры функционально зависят от входных значений ситуационных признаков.

Каждой ситуации соответствует только одно действие.

Обозначим ситуацию как s. Тогда, действия для каждой ситуации обозначим как:

s_i -> a_i (p_i) ,

где p_i = f_i ( n, q, t, v) – параметры действия относительно заданной ситуации.

Каждому действию a_i сопоставляется некоторая степень предпочтения α_i ∈ [0,1]_. База нечетких ситуаций не должна содержать конфликтов: действия, которые соответствуют ситуациям, которые могут быть выполнены одновременно (с заданным порогом α) не должны иметь одинаковую степень предпочтения.

Каждая ситуация s_i задана на множестве ситуационных признаков Y. При идентификации данной ситуации происходит нахождение ее степени выполнения m(s_i , s_в), где s_в, - входная ситуация. Вычисляется результат идентификации признака p_j , например, на основании показателя близости, предложенного в [3].

Рассмотрим предлагаемый способ поддержки принятия решений на основе прецедентной модели.

Этап 1. Предварительная обработка временного ряда. Составление четкого прецедента для сравнения с базой нечетких прецедентов.

Этап 2. Получение прогноза развития временного ряда на основе модели нечетких прецедентов.

Если результат идентификации положительный, то переходим к этапу 3. Иначе – переходим к этапу 4.

Этап 3. Рассчитаем величины n, q, t, v.

Этап 4. Проведем идентификацию нечетких ситуаций (набор нечетких ситуаций должен предусматривать выбор некоторого действия по умолчанию для случая отсутствия прогноза).

Этап 5. Для сработавших ситуации s_i определяется список соответствующих им действий i:

.

Из полученных действий выбирается такое действие , у которого степень предпочтения будет наибольшей:

Этап 6. Для выбранного действия рассчитываются значения его параметров.

Рассмотрим предложенный способ на примере

Опишем базу ситуаций. Пусть эталонной ситуации s₁ соответствует случай: направление курса n = “рост” и запас по времени T = “большой” и запас по амплитуде A = “большой”, возможность влияния новостей v = “низкая”, то действие a₁ = “купить”, уровень потерь = “10% от запаса по амплитуде”, уровень фиксации прибыли = “текущее значение + 90% запаса по амплитуде”

Опишем эталонную ситуацию s₂. Она будет отличаться лишь тем, что запас по амплитуде А = “средний”. Данной ситуации будет соответствовать действие a₂ = “купить”, уровень потерь = “5% от запаса по амплитуде”, уровень фиксации прибыли = “текущее значение + 80% запаса по амплитуде”.

Графики нечётких значений (термов “низкий”, “средний”, “высокий”) признака “запас по амплитуде” представлены на Рисунке 2.

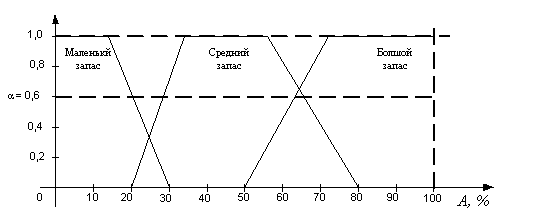
Рисунок 2 – Нечёткие значения признака “запас по амплитуде”

Как видно, например, при значении запаса по амплитуде 65% и пороге срабатывания ситуации 0,6 и при выполнении остальных признаков, срабатывают обе ситуации из данного примера. Следовательно, действия a₁ и a₂ должны иметь разные степени предпочтения.

Предпочтение отдадим более консервативному решению a₂, задав α₂ > α₁.

Заключение

Таким образом, предложенные способ и модель поддержки принятия решений позволяют за счёт совместного применения модели нечёткого прецедента и модели вида “ситуация-действие” автоматизировать процесс применения экспертных знаний о типовых сценариях развития системной динамики с учётом системы предпочтений принимаемых решений. База знаний модели при этом состоит из 2-х основных компонентов: базы эталонных нечётких ситуаций и базы нечётких прецедентов.

литература

1. Зернов М.М., Чуль А.Д. Модель нечёткого прецедента для идентификации реализаций паттерна волновой теории Эллиотта // Известия СмолГУ. – Смоленск: Издательство СмолГУ, 2014. №2 (26).

2. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечёткой логикой. М.: Наука, 1990. – 272 с.

3. Зернов М.М. Оценка состояния объекта управления в случае нечётко-множественной входной информации //Математическая морфология. Электронный математический и медико-биологический журнал. – Т. 6. – Вып. 2. – 2007. Режим доступа к журн.: http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

The method of making decision support based on complex model using fuzzy precedent model and “situation-action” model

Zernov M. M., Kurdakov K. A.

Complex model and method of making decision support using results of time series prediction differing by cooperative application of fuzzy precedent and “situation-action” models are offered. Making decision support bases on prediction of magnitude and duration up to end of phase of quasi linear time series dynamics towards its current change direction. The source of prediction is base of fuzzy precedents (time series dynamics typical scenarios). Calculated values of prediction characteristics are included into situation signs stuff for “situation-action” and are accounted while controlling actions parameters calculating. Offered model and method are considered concerning for task of making decision about purchase/sale on financial market.

Key words: time series analysis, fuzzy precedent, fuzzy scenario, making decision support, situational models.

Зернов Михаил Михайлович – к.т.н., филиал ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске,

Курдаков Кирилл Андреевич – магистрант филиала ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске.

Кафедра вычислительной техники

Филиал ФГБОУ ВПО "НИУ МЭИ" в г. Смоленске.

Поступила в редакцию 21.05.2014.