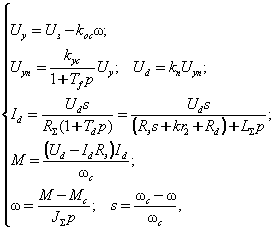Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 14. -

Вып. 1. - 2015. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-45-html/TITL-45.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-45-html/cont.htm

 

УДК 62-83 (06)

 

Методика синтеза асинхронного электропривода с фазовым регулированием в роторе

 

Ó 2014 г. Барышников В. А.

 

(baryshnikov.doc)

 

Рассмотрена замкнутая система асинхронного электропривода с фазовым регулированием в роторе, имеющая суммирующий усилитель и обратную связь по скорости вращения двигателя. На основании схемы замещения асинхронного двигателя по цепи выпрямленного тока ротора дано математическое описание рассматриваемой системы и его линеаризация «в малом». Определена эквивалентная структурная схема замещения и точка коррекции системы, для которой предложена методика синтеза с помощью логарифмических частотных характеристик. Моделирование переходных процессов «в большом» подтверждает эффективность и точность предложенной методики синтеза.

Ключевые слова: асинхронный электропривод, логарифмические частотные характеристики.

 

Находящиеся в эксплуатации и вновь создаваемые электроприводы на базе асинхронных двигателей с фазным ротором представляют собой широкое поле деятельности для модернизации, например, кранового электропривода, а также разработки и внедрения новых систем [1].

К достоинствам фазового регулирования в роторной цепи асинхронного двигателя можно отнести следующее: 1) преобразование не всей энергии, потребляемой двигателем, а только ее части – энергии скольжения; 2) вынесение потерь за пределы двигателя с целью уменьшения его нагрева; 3) существенное снижение влияния на сеть высокочастотных гармоник тока и напряжения, поскольку двигатель проявляет себя как фильтр низких частот, что упрощает и удешевляет использование фильтро-компенсирующих  устройств, если это необходимо; 4) реализация предварительного подключения (предвключения) статорной обмотки на напряжение сети при отключенной роторной обмотке с целью обеспечения затухания переходных процессов, обусловленных электромагнитной инерцией двигателя.

Включение управляемого трехфазного мостового выпрямителя позволяет:

– достичь хорошей управляемости электропривода при достаточно высоком качестве регулирования простыми техническими средствами в замкнутой системе;

– выделить несложным путем ЭДС ротора в качестве обратной связи и избавиться от необходимости применения тахогенератора при не очень высоких требованиях к показателям регулирования;

– реализовать синхронное и синфазное вращение роторов двигателей, используя систему электрического вала с рабочими машинами;  

– повысить энергетические показатели электропривода путем

·        рекуперации энергии скольжения за вычетом потерь в сеть (асинхронный вентильный каскад) или возвращения на вал двигателя (электромеханический каскад);

·        применения схемы динамического торможения с самовозбуждением.

Вопросы синтеза рассматриваемой системы асинхронного электропривода с фазовым регулированием в роторе практически не изучены и поэтому представляют актуальную задачу.

Замкнутая система с суммирующим усилителем и обратной связью (ОС) по скорости является одним из самых простых вариантов реализации системы стабилизации скорости. При разработке такой системы на первом этапе стремятся обеспечить технологические требования, предъявляемые к показателям регулирования в установившемся режиме, а затем следует этап анализа и синтеза исследуемой системы. Синтез заключается в выборе корректирующих звеньев и расчете их параметров для обеспечения требуемых динамических показателей качества регулирования с сохранением свойств системы в установившемся режиме.

Математическое описание замкнутой системы базируется на схеме замещения асинхронного двигателя по цепи выпрямленного тока ротора [2]. С целью упрощения преобразователь в цепи ротора представлен безинерционным звеном с коэффициентом усиления kп, полученным из регулировочной характеристики при неподвижном роторе.

Система уравнений в операторной форме имеет вид:

 

(1)

 

где Uз, Uу и Uуп – соответственно сигнал задания, на входе суммирующего усилителя и на входе преобразователя; Ud – ЭДС на выходе преобразователя; koc и kуc – соответственно коэффициент ОС по скорости и усилителя; ω – угловая скорость вращения двигателя, ωс – синхронное её значение; s – скольжение; Id – выпрямленный ток ротора; М – электромагнитный момент двигателя; Мс – момент сопротивления; JΣ – суммарный момент инерции, приведённый к валу двигателя;   – эквивалентное сопротивление,  – суммарное сопротивление цепи выпрямленного тока:  и  – фазные сопротивления соответственно статора и ротора, приведённые к ротору,  – сопротивление в цепи нагрузки преобразователя, xд – индуктивное сопротивление фазы двигателя;  – суммарная индуктивность:  – индуктивность фазы двигателя,  – индуктивность в цепи нагрузки преобразователя;  – электромагнитная постоянная времени силовой цепи; Tf  – постоянная времени фильтра.

В (1) k – коэффициент приведения фазных параметров и координат цепи переменного тока к цепи выпрямленного тока, линейно зависящий от угла коммутации. Структурная схема замкнутой системы изображена на рис.1 без детализации формирования коэффициента k.

В инженерной практике для синтеза замкнутых систем наиболее часто применяется графоаналитический метод ЛЧХ, который основывается на построении логарифмических частотных характеристик разомкнутой системы,  под которой подразумевается замкнутая система с оборванной обратной связью. Структурная схема содержит переменные коэффициенты и произведения переменных, т.е. объект регулирования является существенно нелинейным. Чтобы вести синтез исследуемой системы методом ЛЧХ, который применим лишь для линейных систем, проведем её линеаризацию «в малом».

 

 

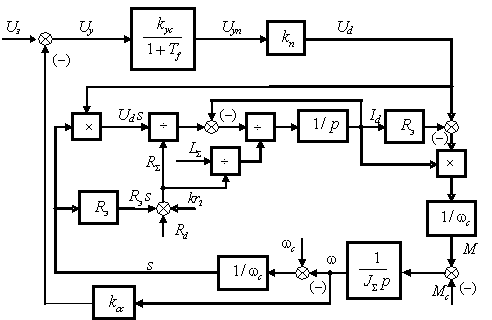
Рисунок 1 - Структурная схема замкнутой системы с суммирующим усилителем и ОС

по скорости после допущений и упрощений

 

При линеаризации систем «в малом» переменные в системе уравнений подвергаются разложению в ряд Тейлора. С учетом только первого члена этого ряда каждая переменная, например, x представляется в виде суммы установившегося значения x0 и приращения Δx, т.е. x = x0 + Δx. После подстановки этих переменных в (1) можно после некоторых преобразований выделить две системы уравнений – относительно установившихся значений и относительно приращений. В процессе преобразований пренебрегаем вторым порядком малости и отклонением относительно точки равновесия коэффициентов kn и k.

Значения переменных x0 определяются путем выборки из данных расчета статических характеристик замкнутой системы. В соответствии с  математическим описанием относительно приращений переменных получим структурную схему линеаризованной системы, в которой пренебрегаем внутренней отрицательной ОС по ЭДС двигателя. Тогда после эквивалентных преобразований структурная схема линеаризованной разомкнутой системы примет вид, представленный на рис.2.

 

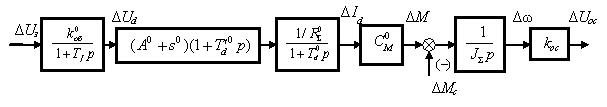
Рисунок 2 – Преобразованная структурная схема линеаризованной

разомкнутой системы

Здесь  – объединенный коэффициент усиления; – коэффициент;  – постоянная времени форсирующего звена, появившегося после преобразований; :;

;  – коэффициент пропорциональности между выпрямленным током и моментом двигателя.

В соответствии с рис.2 передаточная функция разомкнутой линеаризованной системы

 

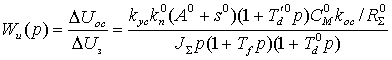 (2)

Проведенный анализ показывает, что в пределах статической характеристики постоянные времени  и отличаются друг от друга незначительно, т.е. звенья с этими постоянными времени практически взаимно компенсируются, а общий коэффициент усиления системы имеет наибольшее значение при максимальном моменте, причем с повышением заданной скорости стабилизации он имеет склонность к снижению. Отсюда следует вывод, что коррекцию системы необходимо вести для расчетного коэффициента усиления системы на характеристике замкнутой системы с пониженной скоростью при максимальном моменте – этот случай и будет наихудшим вариантом, т.е. рекомендуемой точкой коррекции системы, которая выбирается из бесчисленного множества точек равновесия.

При анализе и синтезе системы с помощью логарифмических частотных характеристик ЛЧХ будем руководствоваться общепринятыми положениями и рекомендациями теории автоматического управления [3].

На рис.3 изображены ЛЧХ линеаризованной системы с фазовым регулированием в роторе, имеющей асинхронный двигатель МТН311-6 мощностью 11 кВт, для характеристики с пониженной скоростью в точке равновесия М*=2,4; ω*=0,1965. ЛАЧХ Lи(Ω) и ЛФЧХ φи(Ω) исходной (нескорректированной) системы соответствуют колебательному звену, т.е. системе второго порядка, что подтверждает факт взаимной компенсации форсирующего и инерционного звеньев с постоянными времени  и . По рис.3 видно, что частота среза Ωср и находится на участке ЛАЧХ с наклоном – 40 дБ/дек, а запас по фазе Δφ(Ω)и составляет всего 0,18 рад/с или 10,5º. Это свидетельствует о высокой колебательности системы и низком качестве переходных процессов. Желаемая ЛАЧХ Lж(Ω) построена с учетом рекомендуемых условий и имеет на частоте среза Ωср ж наклон – 20 дБ/дек и запас по фазе Δφж(Ω)=69º.

 

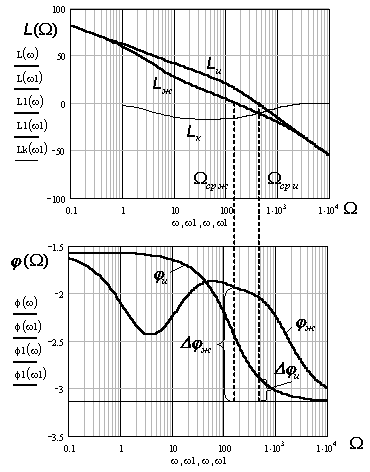
Рисунок 3 – ЛАЧХ L(Ω) и ЛФЧХ φ(Ω) линеаризованной системы с суммирующим усилителем в точке коррекции при kус=200

 

При последовательной коррекции ЛАЧХ корректирующего устройства Lк(Ω) = Lж(Ω) – Lи(Ω). Для рассматриваемого случая Lк(Ω) соответствует передаточная функция

 

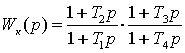 (3)

 

Сама корректирующая цепь устанавливается после суммирующего усилителя. Тогда передаточная функция скорректированной разомкнутой системы

 

Wж(р)= Wи(р) Wк(р).

 

На рис.4 изображены переходные процессы «в большом» пуска замкнутой системы с задатчиком интенсивности на характеристику с пониженной скоростью, на промежуточную и основную характеристики при kус=200. Такой пуск выбран, чтобы минимизировать влияние ограничений, которые обусловлены граничной реостатной характеристикой, насыщением усилителей и системой импульсно-фазового управления,  и тем самым более наглядно проиллюстрировать действие коррекции. Большую колебательность момента и тока нескорректированной системы демонстрируют процессы на рис.4,а, которые промоделированы с помощью упрощенной модели на базе схемы замещения асинхронного двигателя по цепи выпрямленного тока ротора. На этой же модели получен переходный процесс пуска скорректированной системы с расчетными параметрами Wк(р), который дан на рис.4,б. С теми же параметрами процесс пуска с предвключением статора изображен на рис.4,в, но уже по полной модели, учитывающей электромагнитную инерцию асинхронного двигателя. Во всех случаях пуск происходит под реактивной номинальной нагрузкой с моментом инерции JΣ=1,25Jдв, в момент времени t=0,5 с происходит вывод пусковой ступени Rd=0,44 Ом (на рис.4.18,в это время сдвинуто на период предвключения 0,1 с).

Сравнение процессов на рис.4,а и рис.4,б показывает, что применение коррекции полностью устраняет колебательность системы. Графики рис.4,в на начальном этапе пуска сопровождаются бросками момента, максимум которых достигает 2,6Мн, что сопряжено с влиянием электромагнитных переходных процессов в двигателе. Переход на промежуточную характеристику уже лишен этого влияния, и средние значения момента и выпрямленного тока совпадают с аналогичным участком на рис.4,б.

Высокочастотные пульсации момента обусловлены дискретностью работы тиристорного преобразователя. Броски момента и тока на участке разгона до высокой скорости происходят вследствие шунтирования пусковой ступени в цепи выпрямленного тока ротора.

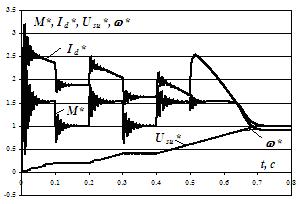
а)

 

 

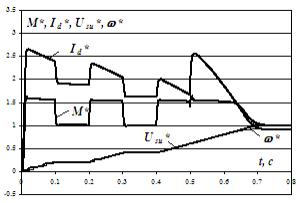
б)

 

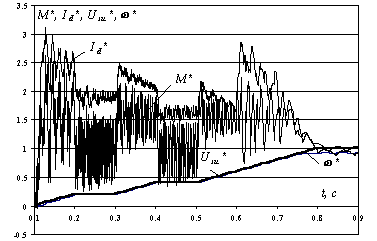
в)

 

Рисунок 4 – Переходные процессы моделирования пуска исследуемой системы на пониженную, промежуточную основную скорость при kус=200: а и б – по упрощенной модели, в – по полной модели

 

Анализируя приведенные на рис.4 графики переходных процессов с помощью моделей в среде Matlab/Simulink, можно сделать вывод, что скорректированная система исследуемого электропривода обладает высокой точностью (статическая ошибка по скорости не превышает 0,5%) и хорошими динамическими показателями качества регулирования, которые подтверждают эффективность и точность предложенной методики синтеза.

 

Литература

 

1.     Барышников В.А. Асинхронный электропривод с фазовым регулированием в роторной цепи // Машиностроение. Энциклопедия /ред. совет: К.В. Фролов (пред.) и др. М.: Машиностроение. Электроприводы, Т. IV-2 /Л.Б. Масандилов, Ю.Н. Сергиевский, С.К. Козырев и др.; под общ. ред. Л.Б. Масандилова, 2012. С. 306 –310.

2.     Барышников В.А. Схема замещения по цепи выпрямленного тока асинхронного электропривода с управляемым роторным выпрямителем // Вестник МЭИ. 2007. №1. С. 80 –86.

3.     Теория автоматического управления. Ч.1: Учебник / Л.С. Гольдфарб, А.В. Балтрушевич, Г.К. Круг, А.В. Нетушил, Е.Б. Пастернак. под ред. А.В. Нетушила. М.: Высшая школа, 1968. – 424 с.

 

Methods of synthesis of asynchronous electric drive with phase control in rotor

 

Baryshnikov V. A.

 

Considered a closed system of asynchronous motor with phase adjustment of the rotor, which sums the amplifier and feedback on the rotational speed of the engine. Based on equivalent circuit of asynchronous motor rotor current is rectified, the chain is a mathematical description of the system and its linearization "in the small". The equivalent diagram of substitution and dot correction system for which the technique of synthesis using logarithmic frequency characteristics. Simulation of transient processes "in the large" confirms the efficiency and accuracy of the proposed method of synthesis.

Key words: asynchronous motor, logarithmic frequency characteristics.

 

Филиал ФГБОУ ВПО «Национальный исследовательский университет МЭИ» в г. Смоленске

Кафедра «Электромеханические системы»

Поступила в редакцию 10.01.2015.