Математическая
морфология.
Электронный
математический и медико-биологический журнал. - Т. 14. -
Вып. 2. - 2015. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/TITL-46.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/cont.htm
УДК 51-74
Статистические
модели отказов
Ó
2015 г. Лямец Л. Л.*, Якименко И. В.*, Канищев О. А.**
Объектом исследования
являются статистические модели отказов технических изделий, алгоритмы и
методики их исполнения. Цель работы – обоснование возможности применения
математико-статистических методов для построения моделей отказов технических изделий
при наличии малых выборок. В процессе работы
был проведен анализ действующей
нормативно-правовой базы прогнозирования безотказности и обработки
статистических данных об отказах изделий любых видов техники на различных
стадиях жизненного цикла и литературных источников, в которых описаны применяемые математико-статистические
методы. В результате исследования
была получены следующие результаты: дано описание метода анализа
выживаемости, его адаптация и применение
для анализов отказов технических изделий
при наличии малых выборок; приведены
количественные характеристики, используемые в методах анализа выживаемости и
методики их вычисления; описана методика
построения таблицы времен жизни (безотказной работы) и приведен практический
пример вычислений; дано описание моментного метода Каплана-Мейера и его
применения для анализов отказов технических изделий; описана методика построения модели отказов на основе статистического
распределения имеющихся экспериментальных данных, приведен практический пример
вычислений по указанной методике.
Ключевые слова: статистические модели, математико-статистические
методы, модели отказов технических изделий, анализ малых выборок,
анализ выживаемости, таблицы времен жизни, моментный метод Каплана-Мейера.
Решение задач прогнозирования безотказности и
обработки статистических данных об отказах изделий любых видов техники на
различных стадиях жизненного цикла определяется национальным стандартом
Российской Федерации ГОСТ Р 27.004-2009 [1]. Указанный
национальный стандарт устанавливает основные теоретические модели отказов и
определяет математические выражения для вычисления характеристик основных аппроксимирующих
распределений.
Национальный стандарт также определяет основные виды
теоретических статистических распределений, используемых для построения моделей
отказов: экспоненциальное, Вейбулла,
гамма, логарифмически-нормальное, нормальное. Кроме перечисленных теоретических
распределений при решении отдельных задач национальным стандартом рекомендуется
применять также и другие распределения, число которых составляет несколько
десятков. На основе теоретических распределений выводятся математические выражения
для вычисления вероятностных (математических) показателей надежности и безотказной
работы. Фактически речь идет о вычислении количественных характеристик надежности
и безотказной работы на основе некоторых теоретических модельных представлений.
Вопросы практического определения и обоснования математических моделей закона
распределения отказов на основе имеющихся опытных данных, обоснование практической
применимости вероятностных (математических) показателей для количественного
описания надежности и безотказной работы технических изделий остаются за
рамками данного национального стандарта.
Вместе с тем выбор и обоснование теоретического закона
распределения отказов имеет большое значение при исследованиях и практических
оценках надежности. Определение количественных характеристик безотказной работы
по одной и той же исходной статистической информации, но при различных предположениях
о статистическом законе распределения отказов может привести к существенно отличающимся
результатам [2].
Первичным материалом для обоснования теоретического
закона распределения отказов являются результаты спланированных испытаний
опытных образцов. Полученные опытные данные дают основу для построения
эмпирического распределения отказов. Для этой цели можно использовать эмпирическое
кумулятивное распределение или эмпирическую плотность распределения. В
простейшем практическом применении эмпирическое распределение позволяет
визуально оценить степень его соответствия выбранному теоретическому
распределению, но для более строгих выводов этого не достаточно. Необходимо проверить
статистическую гипотезу о предполагаемом теоретическом распределении более
точными методами. Такими методами, применяемыми для проверки согласованности
эмпирических данных с гипотезой о предполагаемом теоретическом законе распределения,
являются критерии согласия [3].
Критерии согласия позволяют выявить значимое отличие анализируемого
эмпирического распределения от выбранного теоретического распределения и обоснованно
утверждать о том, что найденное расхождение между этими распределениями существенно
и выбранное в качестве модели теоретическое распределение принципиально не
согласуется с эмпирическими данными. В случае, когда значимое отличие не
выявлено, то этот результат указывает на то, что расхождение между эмпирическим
и теоретическим распределениями вызвано
случайными обстоятельствами и не выходит за пределы статистической ошибки,
связанной, например, с малым объемом выборочных опытных испытаний. В этом
случае выбранное теоретическое распределение может обоснованно служить
адекватной моделью исследуемого эмпирического распределения.
Следовательно, задача практической
реализации критерия согласия состоит в том, чтобы вычислить характеристики
эмпирического распределения, соответствующие характеристикам выбранного теоретического
распределения, выявить и количественно оценить различие между теоретическим и
эмпирическим распределениями и, исходя из полученного результата сделать выводы
о согласии теоретического распределения с эмпирическим, полученным на основе выборочных
данных. На практике применяются
критерии Пирсона, Колмогорова-Смирнова и другие критерии согласия [3].
Для практической реализации критериев согласия
необходимо иметь в распоряжении выборочные экспериментальные данные достаточно
большого объема. Выборочные данные или выборка условно считается малой, если ее
объем меньше 30 единиц наблюдений. Следовательно, для корректной реализации
критериев согласия при заданной ошибке первого рода и обозначенной
чувствительности критерия необходимо иметь выборки достаточно большого объема.
Практически это условие, как правило, трудно обеспечить.
Следует отметить, что кроме проверки гипотезы о
предполагаемом теоретическом законе распределения, статистический анализ
опытных данных является основой для определения статистических показателей
надежности и безотказной работы.
В реальных условиях описанное выше корректное
обоснование математических моделей и вычисление на их основе вероятностных
(математических) показателей надежности и безотказной работы трудновыполнимо по
причине больших ресурсных затрат. Поэтому на практике более рациональным действием
является применение методов статистического анализа экспериментальных данных,
которые позволяют вычислить статистические показатели надежности и безотказной
работы на основе анализа выборок малого объема.
Для вычисления количественных характеристик надежности
и безотказной работы могут быть использованы статистические методы анализа
первичных данных, объединенные под общим названием «Анализ выживаемости» [4,
5].
Первоначально разработанные методы анализа
выживаемости были ориентированы для проведения медико-биологических
исследований с учетом их специфики. В настоящее время практически апробированные
методы анализа выживаемости успешно применяются для статистического анализа в
технических областях, в том числе они могут быть применимы и к анализу
надежности и безотказной работы технических изделий.
С формальной стороны при использовании методов анализа
выживаемости исследуемой переменной является время, которое прошло от начала наблюдения
до наступления критического события. Определение сущности критического события
дается в каждом конкретном случае с учетом специфики предметной области. Например,
при анализе надежности и безотказной работы критическим событием может быть
отказ работы технического изделия.
Особенность методов анализа выживаемости состоит в
том, что они предназначены для анализа цензурированных первичных данных. Исходные
данные могут быть цензурированными справа (наблюдение завершилось до
наступления критического события), цензурированными слева или цензурированными
как справа, так и слева [6, 7, 8]. В дальнейшем в целях конкретизации
предлагаемых методов анализа изложение будет касаться данных наблюдений,
цензурированных справа.
По своей сути цензурирование
при анализе надежности и безотказной работы имеет место в том случае, когда
имеется лишь некоторая информация о времени работы технического изделия, но
точное время безотказной работы не всегда может быть известно.
Цензурированные данные представляют собой результат
наблюдения за исследуемым техническим объектом (единицей наблюдения) до
наступления некоторого критического события. Цензурированные данные дают
возможность описывать поведение исследуемой единицы наблюдения с учетом того,
что наблюдение в точности до наступления отказа не всегда возможно. Наблюдение
за объектом может стать невозможным до наступления отказа. В таких случаях следует
говорить только о том, что время до наступления отказа не меньше времени окончания
наблюдения. Время наступления отказа является цензурированным. В практике
количественной оценки надежности и безотказной работы технических изделий цензурирование является ключевой аналитической проблемой,
для решения которой разработаны специальные методы анализа экспериментальных данных.
Можно выделить две основные причины возникновения
цензурированных данных:
- критическое событие для наблюдаемого технического
объекта в течение периода наблюдения не наступило;
- технический объект выбыл из-под наблюдения в
исправном состоянии до окончания периода наблюдения (потерян из виду), и
критическое событие за время наблюдения зафиксировано не было.
Для применения методов анализа выживаемости
необходимо, чтобы организация исследования удовлетворяла следующим условиям.
1. Время начала и завершения наблюдения должно быть
точно известно для каждой единицы наблюдения.
2. Для каждой единицы наблюдения должны быть точно
установлены:
- факт и время наступления
критического события, если оно произошло в течение периода наблюдения;
- факт выбытия единицы наблюдения до окончания периода
наблюдения;
- факт не наступления критического события в течение
периода наблюдения.
3. Единицы наблюдения должны представлять собой выборочную статистическую совокупность
(выборку), которая должна отвечать требованиям репрезентативности. Методы
отбора единиц наблюдения в выборочную совокупность определяются в соответствии
предметной областью проводимых наблюдений и возможностью практической реализации
механизмов отбора.
Особенности цензурированных данных должны быть учтены
при разработке протоколов наблюдений, проводимых с целью анализа надежности и
безотказной работы технических изделий.
Практический пример табличного представления
эмпирических данных при наличии цензурированных измерений приведен ниже в
таблице 1. В данном примере предполагается, что период наблюдения T одинаков для всех единиц наблюдения и определяется
целями и задачами испытаний.
В приведенном примере для объекта A критическое
событие наступило до окончания периода наблюдения T. Время наступления критического события является нецензурированным.
Для объектов B и C время их наблюдения в
исправном состоянии является цензурированным справа. Объект B
оставался исправным до полного окончания установленного периода наблюдения T, критическое событие не наступило. Объект C выбыл
из-под наблюдения в исправном состоянии раньше окончания периода наблюдения T,
критическое событие также не наступило.
Методы анализа выживаемости позволяют использовать все
имеющиеся экспериментальные данные, то есть анализировать как цензурированные,
так и нецензурированные наблюдения и не терять с
трудом собранную информацию о времени, в течение которого объект оставался в исправном
состоянии.
Основными количественными характеристиками, которые
вычисляются по экспериментальным данным методами анализа выживаемости, являются
функция выживаемости ![]() и функция интенсивности рисков
и функция интенсивности рисков ![]() .
.
Функция выживаемости ![]() применительно к анализу надежности и безотказной
работы определяет вероятность единицы наблюдения находиться в исправном
состоянии в любые моменты времени в течение периода наблюдения T. Эту вероятность также называют выживаемостью.
Функцией выживаемости можно в вероятностных категориях описывать поведение
самых разнообразных объектов и в тех случаях, когда в качестве критического
события может выступать любое формально определенное событие.
применительно к анализу надежности и безотказной
работы определяет вероятность единицы наблюдения находиться в исправном
состоянии в любые моменты времени в течение периода наблюдения T. Эту вероятность также называют выживаемостью.
Функцией выживаемости можно в вероятностных категориях описывать поведение
самых разнообразных объектов и в тех случаях, когда в качестве критического
события может выступать любое формально определенное событие.
Таблица 1
Пример представления результатов наблюдения при
наличии
цензурированных данных
|
Единицы наблюдения (объекты) |
Время начала наблюдения
|
Время окончания наблюдения
|
Время наблюдения объекта в исправном состоянии
|
Результаты наблюдения |
|
А |
|
|
|
Объект A наблюдали от временного отсчета |
|
B |
|
|
|
Объект B наблюдали от временного отсчета |
|
C |
|
|
|
Объект C наблюдали
от временного отсчета |
Для изучаемой статистической совокупности
выживаемостью ![]() называется вероятность «прожить» или оставаться в
исправном состоянии более времени t с
момента начала наблюдения. Формальная запись имеет вид
называется вероятность «прожить» или оставаться в
исправном состоянии более времени t с
момента начала наблюдения. Формальная запись имеет вид
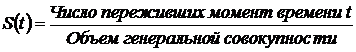 (1)
(1)
Типичный вид графика теоретической функции выживаемости
показан на рис. 1.
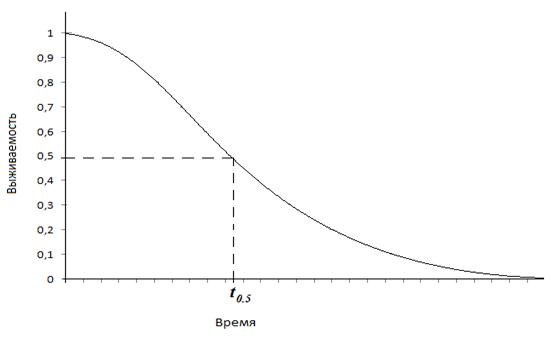
Рис. 1. Типичный вид графика теоретической функции
выживаемости ![]()
В точке ![]() , соответствующей началу наблюдения, выживаемость
равна 1. По мере увеличения времени наблюдения выживаемость уменьшается и стремится
к нулю. Момент времени
, соответствующей началу наблюдения, выживаемость
равна 1. По мере увеличения времени наблюдения выживаемость уменьшается и стремится
к нулю. Момент времени ![]() до которого доживает или сохраняет свою работоспособность
50% единиц наблюдения исследуемой статистической совокупности, называется
медианой выживаемости. Формально
до которого доживает или сохраняет свою работоспособность
50% единиц наблюдения исследуемой статистической совокупности, называется
медианой выживаемости. Формально ![]() .
.
Исследование генеральной статистической совокупности
сплошным методом в практических условиях не представляется возможным в силу
больших ресурсных затрат, поэтому обычно исследование проводят выборочным
методом. Из генеральной совокупности при помощи научно и практически обоснованных
методов, зависящих от предметной области исследования, формируется
репрезентативная выборочная совокупность или выборка. Анализ выборочной совокупности
позволяет получить оценки генеральных показателей и характеристик, описанных в
вероятностных категориях.
Оценку кривой выживаемости по исследуемой выборочной
совокупности при отсутствии цензурированных данных можно вычислить по формуле:
![]() (2)
(2)
где ![]() – число
единиц наблюдения «переживших» момент времени t; N –
объем изучаемой выборочной статистической совокупности.
– число
единиц наблюдения «переживших» момент времени t; N –
объем изучаемой выборочной статистической совокупности.
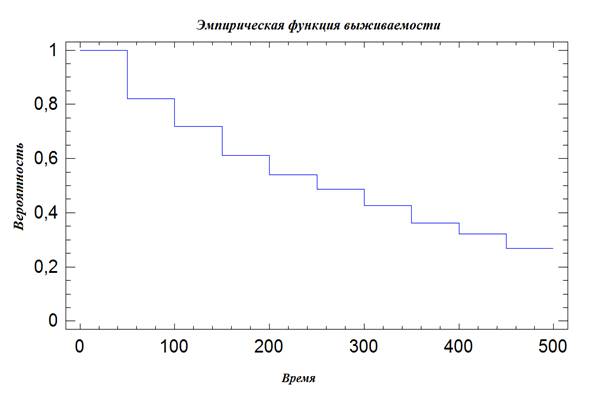
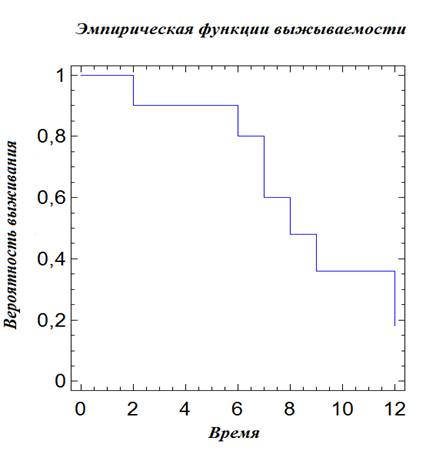
Типичная эмпирическая кривая выживаемости, показанная
на рис. 2, имеет ступенчатый вид.
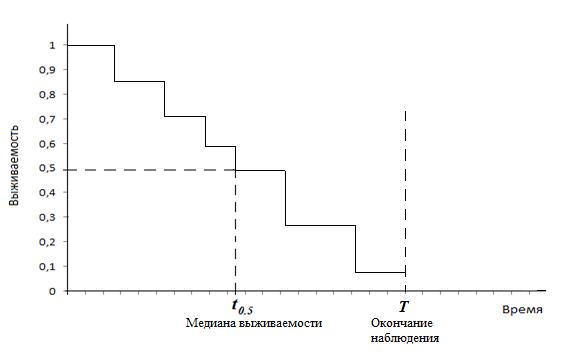
Рис. 2. Вид эмпирической функции выживаемости
Кроме функции выживаемости, важное практическое значение
имеет функция интенсивности рисков ![]() . Формальное определение этой функции имеет вид:
. Формальное определение этой функции имеет вид:
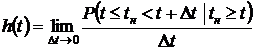 (3)
(3)
Функция интенсивности рисков ![]() определяет
моментный потенциал на единицу времени для критического события (отказа),
которое может произойти, при условии, что единица наблюдения будет
работоспособна до времени t. Так
как числитель выражения (3), по сути,
является условной вероятностью, то функцию интенсивности рисков также называют
условной долей критических событий (отказов).
определяет
моментный потенциал на единицу времени для критического события (отказа),
которое может произойти, при условии, что единица наблюдения будет
работоспособна до времени t. Так
как числитель выражения (3), по сути,
является условной вероятностью, то функцию интенсивности рисков также называют
условной долей критических событий (отказов).
Если функция выживаемости определяет вероятность того,
что критическое событие не произойдет в определенный момент времени t, то функция интенсивности рисков направлена на
количественное описание вероятности того, что событие произойдет в этот момент времени. Поэтому, чем больше значение функции выживаемости для конкретного t, тем меньше для
него функция интенсивности рисков и
наоборот.
Функция выживаемости ![]() и функция интенсивности рисков
и функция интенсивности рисков ![]() взаимосвязаны и могут быть аналитически
выражены одна через другую. Их аналитическая взаимосвязь определяется
выражениями:
взаимосвязаны и могут быть аналитически
выражены одна через другую. Их аналитическая взаимосвязь определяется
выражениями:
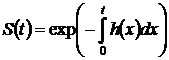
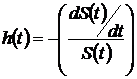
Приведенные выражения носят теоретический характер и
определяют основную идеологию построения методов практического анализа реальных
эмпирических данных.
При количественном описании безотказной работы важно
оценить вероятность того, что единица наблюдения работала больше времени t после начала наблюдения. Эта важная количественная
характеристика, как было указано выше, называется функцией выживаемости.
Практический способ описания функции выживаемости
состоит в построении таблицы времен жизни (таблицы безотказной работы) единиц
наблюдения в изучаемой выборочной совокупности. Это достаточно известный метод
анализа данных о выживаемости. Например, он традиционно используется в страховании,
где такие таблицы называются таблицами дожития.
Более простым является построение интервальных вариационных рядов с равными по величине интервалами. Как было
указано выше исходя из объема выборки N оптимальное число интервалов можно,
например, определить по формуле Стерджесса
![]() ,
,
где N объем выборки.
Ширина каждого интервала будет равна ![]() .
.
По экспериментальным данным для каждого интервала
вычисляется следующие абсолютные показатели:
- число единиц наблюдения ![]() , которые в начале
рассматриваемого интервала с номером i были работоспособны (число в начале);
, которые в начале
рассматриваемого интервала с номером i были работоспособны (число в начале);
- число единиц наблюдения ![]() , которые отказали в интервале
с номером i
(число отказавших) - нецензурированные данные;
, которые отказали в интервале
с номером i
(число отказавших) - нецензурированные данные;
- число единиц наблюдения ![]() изъятых из наблюдения в интервале с номером i (число изъятых) – цензурированные данные;
изъятых из наблюдения в интервале с номером i (число изъятых) – цензурированные данные;
- число изучаемых единиц наблюдения ![]() – это число единиц
наблюдения, которые были работоспособны в начале рассматриваемого временного интервала
с номером i, минус половина от числа изъятых, т.е.
– это число единиц
наблюдения, которые были работоспособны в начале рассматриваемого временного интервала
с номером i, минус половина от числа изъятых, т.е. ![]() ,
,
![]() .
.
Число изучаемых единиц наблюдения ![]() также можно вычислить
по формуле
также можно вычислить
по формуле
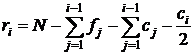 (4)
(4)
В формуле (4) при вычислении числа изучаемых единиц
наблюдения ![]() суммирование проводится
по всем интервалам, предшествующим интервалу с номером i. Очевидно,
что для первого интервала
суммирование проводится
по всем интервалам, предшествующим интервалу с номером i. Очевидно,
что для первого интервала 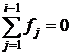 и
и 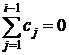 , следовательно,
, следовательно, ![]() .
.
Для понимания таблиц времен жизни важно помнить, в
каждом временном интервале для единицы наблюдения регистрируется либо
наступление критического события или отказ (нецензурированные
наблюдения), либо изъятие (цензурированное наблюдение).
На основании указанных выше абсолютных показателей для
каждого интервала вычисляются следующие относительные показатели (доли).
1. Доля отказавших единиц наблюдения ![]() - это отношение числа
единиц наблюдения
- это отношение числа
единиц наблюдения ![]() , отказавших в соответствующем
интервале с номером i,
к числу единиц наблюдения
, отказавших в соответствующем
интервале с номером i,
к числу единиц наблюдения ![]() , изучаемых на этом интервале, т.е.
, изучаемых на этом интервале, т.е. 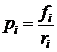 .
.
2. Доля не отказавших в изучаемом интервале единиц
наблюдения ![]() равна единице минус
доля отказавших единиц наблюдения
равна единице минус
доля отказавших единиц наблюдения ![]() , т.е.
, т.е. ![]() .
.
3. Кумулятивная доля не отказавших объектов ![]() - это
кумулятивная доля объектов, которые не отказали к началу соответствующего
временного интервала с номером i. По сути, кумулятивная доля не отказавших объектов
- это
кумулятивная доля объектов, которые не отказали к началу соответствующего
временного интервала с номером i. По сути, кумулятивная доля не отказавших объектов ![]() и является эмпирической
оценкой функции выживаемости
и является эмпирической
оценкой функции выживаемости ![]() , то есть это вероятность
того, что единица наблюдения «переживет» определенный временной интервал.
, то есть это вероятность
того, что единица наблюдения «переживет» определенный временной интервал.
К началу первого временного интервала, являющегося
временем начала наблюдения, ни одна единица наблюдения еще не могла отказать.
Нижние индексы абсолютных и относительных показателей, относящиеся к началу
первого временного интервала (началу наблюдения) можно обозначить через 0. Очевидно, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() и, соответственно,
и, соответственно, ![]() . Для всех
остальных интервалов
. Для всех
остальных интервалов ![]() равна
произведению долей не отказавших объектов по всем предыдущим интервалам.
Формальная запись эмпирической оценки функции выживаемости имеет вид:
равна
произведению долей не отказавших объектов по всем предыдущим интервалам.
Формальная запись эмпирической оценки функции выживаемости имеет вид:
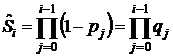 (5)
(5)
Стандартная ошибка эмпирической оценки функции
выживания вычисляется по формуле
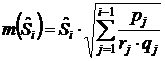 (6)
(6)
Для первого интервала стандартная ошибка эмпирической
оценки функции выживания ![]() .
.
Для последующих интервалов при выполнении вычислений
по формуле (6) суммирование производится по всем предыдущим интервалам.
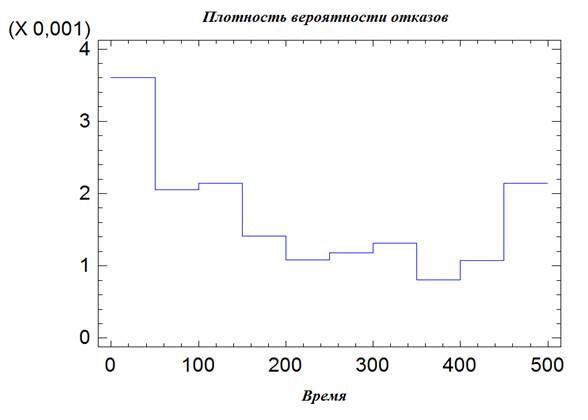
На основе ![]() можно вычислить
эмпирическую оценку плотности
вероятности отказа
можно вычислить
эмпирическую оценку плотности
вероятности отказа ![]() в каждом интервале.
Эмпирическая оценка плотности вероятности отказа временного интервала с номером
i
вычисляется как разность между функцией выживаемости на данном интервале и
функцией выживаемости на следующем интервале, которая делится на ширину этого
интервала. Для вычисления можно использовать следующие формулы:
в каждом интервале.
Эмпирическая оценка плотности вероятности отказа временного интервала с номером
i
вычисляется как разность между функцией выживаемости на данном интервале и
функцией выживаемости на следующем интервале, которая делится на ширину этого
интервала. Для вычисления можно использовать следующие формулы:
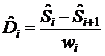 или
или 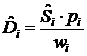
Стандартная ошибка эмпирической функции плотности
вероятности определяется выражением:
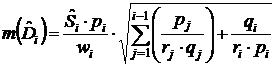 (7)
(7)
В случае, когда
для вычисляемого интервала ![]() , то стандартная ошибка эмпирической функции плотности
вероятности не вычисляется и ее значение принимается равным
нулю.
, то стандартная ошибка эмпирической функции плотности
вероятности не вычисляется и ее значение принимается равным
нулю.
В целях сглаживания эмпирических характеристик в
случаях, когда в действительности для некоторого i-того интервала ![]() и
и ![]() , в расчетах для этого интервала значение
, в расчетах для этого интервала значение ![]() принимают равным 0,5.
принимают равным 0,5.
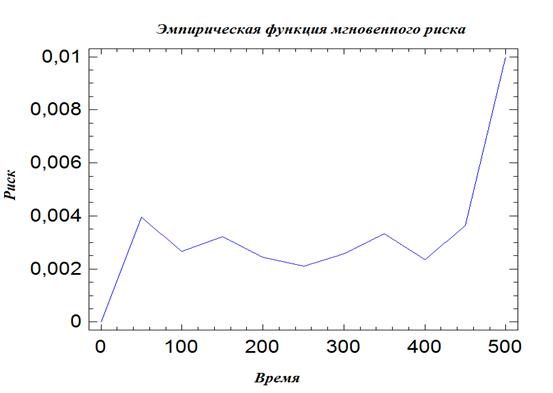
Важной количественной характеристикой является
эмпирическая интенсивность отказов, или эмпирическая функция мгновенного риска ![]() . Эта функция является прогностической
характеристикой, описывающей надежность работы единицы наблюдения. Формально
функция мгновенного риска равна вероятности того, что единица наблюдения
откажет в следующем интервале, при условии, что
в предыдущем интервале она была в рабочем состоянии. Эмпирическая оценка
функции мгновенного риска
. Эта функция является прогностической
характеристикой, описывающей надежность работы единицы наблюдения. Формально
функция мгновенного риска равна вероятности того, что единица наблюдения
откажет в следующем интервале, при условии, что
в предыдущем интервале она была в рабочем состоянии. Эмпирическая оценка
функции мгновенного риска ![]() вычисляется по
формуле:
вычисляется по
формуле:
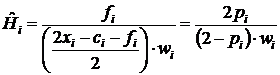 (8)
(8)
Стандартная ошибка оценки функции мгновенного риска
определяется выражением:
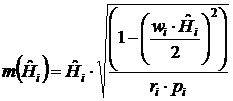 (9)
(9)
В случае, когда
для вычисляемого интервала ![]() , то стандартная ошибка функции мгновенного риска не
вычисляется и ее значение принимается равным нулю.
, то стандартная ошибка функции мгновенного риска не
вычисляется и ее значение принимается равным нулю.
Для количественной характеристики эмпирической оценки
функции выживания используется медиана выживаемости ![]() . Это точка на временной оси,
в которой кумулятивная функция выживаемости наиболее близка 0,5. Для вычисления
медианы необходимо найти временной интервал, в котором значение функции
. Это точка на временной оси,
в которой кумулятивная функция выживаемости наиболее близка 0,5. Для вычисления
медианы необходимо найти временной интервал, в котором значение функции ![]() наиболее близко
к значению
наиболее близко
к значению ![]() , но больше или равно этому
значению. Такой интервал будем называть медианным.
, но больше или равно этому
значению. Такой интервал будем называть медианным.
Эмпирическая оценка медианы выживаемости может быть
вычислена способом линейной интерполяции по формуле
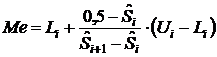 (10)
(10)
где ![]() и
и ![]() - соответственно нижняя и
верхняя границы медианного интервала, а
- соответственно нижняя и
верхняя границы медианного интервала, а ![]() и
и ![]() - значения
кумулятивной функции выживаемости соответственно в медианном интервале (интервал
с номером i)
и интервале, следующим за ним (интервал с номером i+1).
- значения
кумулятивной функции выживаемости соответственно в медианном интервале (интервал
с номером i)
и интервале, следующим за ним (интервал с номером i+1).
Стандартная ошибка медианы вычисляется по формуле
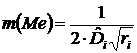 (11)
(11)
где ![]() - значение
эмпирической функции плотности вероятности в медианном интервале, а
- значение
эмпирической функции плотности вероятности в медианном интервале, а ![]() - число изучаемых единиц наблюдения в медианном
интервале.
- число изучаемых единиц наблюдения в медианном
интервале.
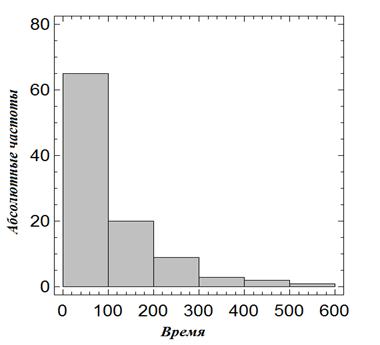
Ниже в таблице 2 приведен пример вычислений указанных
выше вероятностных показателей таблицы
времен жизни для выборки объемом ![]() единиц наблюдения. Период
наблюдения объектов составлял
единиц наблюдения. Период
наблюдения объектов составлял ![]() часов и разбивался на
десять интервалов. Число интервалов в данном случае не оптимизировалось по
формуле Стерждесса и определялось целями
исследования.
часов и разбивался на
десять интервалов. Число интервалов в данном случае не оптимизировалось по
формуле Стерждесса и определялось целями
исследования.
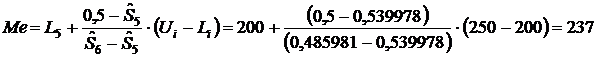 .
.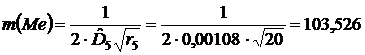 .
.
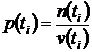
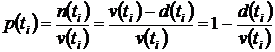
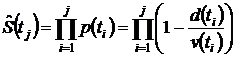
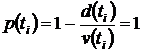 .
.

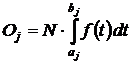
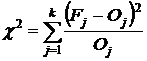 .
.