Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 14. -

Вып. 2. - 2015. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/TITL-46.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/cont.htm

Тайна «золотого» сердца

В. Д. ЦВЕТКОВ

СЕРДЦЕ, ЗОЛОТАЯ ГАРМОНИЯ И ОПТИМАЛЬНОСТЬ

график.jpg

РОССИЙСКАЯ АКАДЕМИЯ НАУК

ПУЩИНСКИЙ НАУЧНЫЙ ЦЕНТР

ИНСТИТУТ ТЕОРЕТИЧЕСКОЙ И ЭКСПЕРИМЕНТАЛЬНОЙ БИОФИЗИКИ

В.Д. ЦВЕТКОВ

СЕРДЦЕ, ЗОЛОТАЯ ГАРМОНИЯ И ОПТИМАЛЬНОСТЬ

Новые аспекты организации деятельности сердца

человека и млекопитающих

Пущино 2014

УДК 573.22+599+612.176

ББК 30.16

Ц 26

(tsvetkov.doc)

Книга знакомит читателей с Гармонией сердца - одного из самых удивительных творений Природы. Показано, что работа сердца основана на оптимальном сопряжении (гармонии) «противоположностей» во всех сердечных системах различной сложности и назначения. На основе системного анализа экспериментальных данных отечественных и зарубежных исследователей автором впервые выдвинут и обоснован оптимальный критерий гармонии сердца человека и млекопитающих – принцип оптимального вхождения. В соответствии с этим принципом, «каждая из «простых» сердечных систем, совместно образующих «сложную» кардиосистему, включена в последнюю оптимальным образом, вследствие чего сложная система исполняет свою функцию с минимальными затратами энергии и строительного материала». Установленный принцип позволяет ответить на вопрос: «Почему Природа избрала существующий вариант конструкции сердца, а не какой-либо другой?». Показано, что основа деятельности любой системы сердца, независимо от уровня ее сложности и назначения, – это оптимальное энерго-вещественное сопряжение входящих в нее «простых» систем. В каждой из «простых» систем, составляющих сложную систему, присутствует дуальность оптимальных «противоположностей», обеспечивающих наиболее эффективную работу всей сложной системы в целом. Показано, что во многих сердечных системах оптимальность гармонии «противоположностей» обеспечивается уникальными математическими свойствами пропорции золотого сечения и чисел ряда Фибоначчи. Золотая гармония «противоположностей» выступает как своего рода «знак» высшего энерго-вещественного «качества» сердечных систем и всего сердца в целом.

Книга предназначена для широкого круга специалистов, интересующихся самоорганизацией и гармонией живых систем.

Цветков Виктор Дмитриевич

Сердце, золотая гармония и оптимальность

Новые аспекты организации деятельности сердца человека и млекопитающих

Издание второе, переработанное и дополненное

Первое издание вышло под названием «Золотая гармония и сердце» (Пущино, 2008 г.)

Ответственный редактор: доктор технических наук, проф. И.И. Свентицкий

Рецензент: доктор медицинских наук, проф. В.А. Глотов

Книга издана по рекомендации Ученого совета Института теоретической и экспериментальной биофизики РАН

Предисловие

Состояние современной биологии таково, что требуются общенаучные концепции и разработки, призванные, с одной стороны, закрыть «узкие места» биологических наук, а с другой – выработать универсальные подходы к решению проблем с привлечением новых методов и идей. На этом фоне особенно перспективными представляются общенаучные положения: гармония, симметрия и оптимальность. Тем не менее, в настоящее время вопросы гармонии, симметрии и оптимальности все еще не привлекают должного внимания биологов. По-видимому, это связано с возрастающим сужением кругозора специалистов в каждой отрасли знаний. Бесконечное дробление исследуемого живого объекта на части приводит к тому, что за «деревьями» все труднее увидеть «лес». Возрастающая детализация препятствует решению важнейшей задачи – выявлению теоретической (математической) основы сопряжения в единое целое живых систем различных иерархических уровней. В исследовании В.Д. Цветкова представлено решение этой задачи на конкретном биологическом объекте – сердце человека и млекопитающих.

Книга В.Д. Цветкова – четвертая в серии его монографий^1-3, посвященных анализу сердечной деятельности человека и млекопитающих, на основе общей теории систем Ю.А.Урманцева (ОТСУ), положений симметрии, гармонии и самоорганизации. Такой анализ позволил объединить, казалось бы, необъединимое: сердце, гармонию и энергетическую оптимальность. Важнейший общенаучный результат монографий Цветкова – установление естественнонаучной сущности феномена золотой пропорции. Обобщенный анализ многочисленных экспериментальных данных по сердечной деятельности человека и млекопитающих позволил автору открыть проявление золотой пропорции в структурной организации сердца и его сосудистой системы и их функционировании при спокойном состоянии организма. При таком состоянии четыре типа сердечной ритмики строго подчинены золотой пропорции.

В монографии В.Д. Цветкова на основе экспериментальных данных показано, что за «противоположностями» («золотыми сечениями») в сердечных системах неизменно «скрывается» максимальная экономия энергии и живого вещества. Цветков в своих исследованиях впервые установил, что сердце – поистине «золотой орган». Гармония «противоположностей» в структурах наиболее важных сердечных циклов и процессов имеет энергооптимальную структуру, конструктивно представленную золотым сечением и числами Фибоначчи. Автором показано: золотое сечение – это своего рода «технологический рецепт» гармонии, используемый Природой для экономии энергии и живого строительного материала.

Выявленные автором четыре типа закономерностей энергоэкономности позволили заключить, что сущность феномена золотой пропорции можно выразить как психобиологический механизм энергоэкономности. Человек и животные, благодаря их сердечной ритмике по золотой пропорции, неосознанно отделяют все процессы и структуры этого вида энергоэкономности. Подобными природными механизмами энергоэкономности (гармонии) являются также фрактальные структуры, солитоны, фазовые переходы. К подобным механизмам высокой энергоэффективности можно отнести и феноменальные физико-химические принципы (Ферма, наименьшего действия и др.), которые не случайно использованы в качестве исходных позиций при построении физико-химических теорий. Исследуя термодинамические процессы открытых систем, физик-теоретик Ю.Л. Климантович⁴ установил, что в названных и других самоорганизующихся процессах энтропия не возрастает, а уменьшается. Подобные результаты, не согласующиеся со вторым началом термодинамики, были выявлены проф. МГУ А.П. Руденко⁵ при изучении элементарных химических каталитических систем. В недавних исследованиях выявлено, что антиэнтропийные и феноменальные химические принципы объединяет и объясняет закон выживания, сущность которого противоположна второму началу термодинамики. Этот закон и начало логически концептуально объединены в виде зеркальной динамической симметрии в общий принцип естествознания – принцип энергетической экстремальности самоорганизации и прогрессивной эволюции. Этот принцип позволил решить главную проблему биофизики – объединить единой теорией физику и биологию. Все эти результаты в своей основе согласуются с выводами об энергооптимальной гармонии сердечных систем, представленными в книге В.Д. Цветкова. Рассматриваемая и другие книги Цветкова являются важной вехой в решении названной проблемы биофизики и создания единых теоретических основ всеединства знаний. Несомненно, книга В.Д. Цветкова по своему содержанию представляет большую теоретическую и практическую ценность для биологов различного профиля, интересующихся проблемами интеграции и систематизации научных данных.

¹Цветков В.Д. Системная организация деятельности сердца млекопитающих. Пущино, 1993.

2Цветков В.Д. Сердце, золотое сечение и симметрия. Пущино, 1997.

³Цветков В.Д. Кислородное обеспечение сердца и принцип оптимального вхождения. Пущино, 2004.

⁴Климантович Ю.Л. Статистическая теория открытых систем. Т. 1. М.: «Янус», 1995.

⁵Руденко А.П. Самоорганизация и синергетика//Синергетика. М.: МГУ, 2000. Т. 3. С. 61-99.

Главный научный сотрудник

ГНУ ВИЭСХ, академик

Академии проблем сохранения жизни,

доктор технических наук, проф. И.И. Свентицкий

Введение

Религиозность ученого состоит в восторженном преклонении перед законами гармонии.

А. Эйнштейн

Гармония природы является в Форме и Числе.

Д`Арси Томпсон

Самое правильное – самое простое.

Л.А. Арцимович

В современной биологии постоянно возникают новые науки как результат выдающихся открытий в мире живой природы. В «старых» науках происходят процессы дифференциации, появляются новые направления по мере расширения и углубления традиционного «поля поиска». Биология испытывает острую потребность в интегрирующей дисциплине, которая объединяла бы все науки о живом. Таким интегрирующим направлением в биологических и других науках в настоящее время во все большей степени становится учение о Гармонии. Не подлежит сомнению, гармония - важнейшее основание, объединяющее живую природу. Она представляет не только оптимальное сопряжение «противоположностей» в биосистемах, но также высокую устойчивость и стабильность последних. Можно сказать, внешнее и внутреннее совершенство множества биосистем различной сложности и назначения предопределило поиск универсальных законов гармонии, общих для всех живых объектов. Первые значительные усилия в решении этой проблемы были предприняты философами-математиками Древней Греции; они продолжаются и в наши дни. Наиболее значимые результаты в «математическом» направлении были получены в последней четверти 20 и начале 21 века. В связи с этим необходимо отметить важнейшие достижения советских и российских ученых [Урманцев, 1974; Петухов, 1981; Сороко, 1984; Стахов, 1984; Марутаев, 1990; Боднар, 1994; Коробко, 2000; Волошинов, 2000; Шевелев, 2000; Суббота, 2003; Аракелян, 2007; Балакшин, 2008 и др.]. Все перечисленные исследования, так или иначе, связанные с «присутствием» в живых системах золотого сечения и чисел Фибоначчи, представляют значительный вклад в математическое исследование гармонии биосистем. Тем не менее, несмотря на существенное продвижение в «золотом» направлении, выявление универсальной математической основы гармонии живых систем по-прежнему остается одной из важнейших проблем теоретической биологии.

Целью этой книги является обосновать общий критерий и представить математические особенности гармонии одного из шедевров Природы - сердца человека и млекопитающих. В качестве методологического инструментария для решения поставленной задачи автором использованы: системный подход к рассматриваемым сердечным объектам, единство «противоположностей» в этих объектах и принцип оптимального вхождения «простых» сердечных систем в «сложные» (максимальная экономия энергии и вещества). Ниже нами рассмотрены методологические особенности предпринятого исследования.

Выдающийся советский биолог-теоретик А.А. Любищев (1890-1972), размышляя о преемственности идей в современной науке, высказал убеждение в том, что «следуя великому диалектическому закону развития науки, в этом процессе неоднократно придется возвращаться к великим мыслителям Эллады» [103, с. 212]. Учение о Гармонии является краеугольным камнем античной науки, одним из ее величайших достижений. Следует сказать, что со времен древнегреческих философов гармония была и остается «сквозной» идеей, привлекающей внимание многих поколений ученых. Отметим, многие великие ученые не сомневались в присутствии скрытой гармонии в окружающем нас мире и наличии простых законов, отражающих гармонию. Известна, в частности, глубокая убежденность Эйнштейна в том, что «без веры во внутреннюю гармонию нашего мира не могли бы существовать никакие науки. Эта вера есть и всегда останется основным мотивом всякого научного творчества» [222, т. 4, с. 43]. На всех стадиях цивилизации понятия Гармонии и Меры оказывали влияние на различные области искусства, философии, науки, сопутствовали этапам научно-технического прогресса. Интерес к гармонии временами возрастал или, напротив, снижался, но никогда не исчезал. Следует отметить, в наши дни возвращение к древним истокам связано с поисками новых подходов к решению крупных научных, экономических и технических проблем.

Анализ гармонии и сам термин (греч. άρμονία – слаженность, соразмерность частей) впервые представлены в трудах философов Древней Греции. Со времен Древней Греции и до наших дней гармония является универсальным понятием, которое имеет отношение и к Природе, и к творческой деятельности человека. Философские основы учения великого греческого философа Пифагора (570-500 до н.э.) и его учеников состоят в признании гармоничности Вселенной. Главная истина в соответствии с учением Пифагора состоит в том, что гармония объективна, она существует помимо нашего сознания в гармоническом устройстве всего сущего, начиная с Космоса и заканчивая микромиром. Греки предполагали существование простых математических законов, представляющих гармонию. «Греки считали, что закон и порядок существуют в Природе и математика – ключ к пониманию мира. Более того, человеческий разум способен проникнуть в сокровенный план природы и открыть математическую структуру Вселенной» [79, с. 40]. Современное понятие «Гармония» представлено следующим определением: «Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия» [24, т. 6, с. 128]. В этом определении четко просматривается определение гармонии с математической, количественной точки зрения: «соразмерность частей и целого».

С самого начала гармония отождествлялась греками с «противоположностями» в объекте. Мир устроен так, что любое явление обязательно имеет свою противоположность; каждое из них неустранимо и проявляется совместно с альтернативой. Впервые структурное определение гармонии было представлено древнегреческим мыслителем Гераклитом (540-480 до н. э.): «В мире существует единство, но это единство (гармония) образуется сочетанием противоположностей» [по 127, с. 76]. Об этом же писал Аристотель: «Природа стремится к противоположностям и из них, а не подобных вещей, образует созвучие…» [по 151с. 29]. Это суждение по своей сути перекликается с определением гармонии, «озвученным» Гераклитом. Таким образом, Пифагор и его последователи рассматривали природу вещей как конфигурацию «противоположных» качеств. Пифагорейцы считали: «противоположности» должны уравновешивать друг друга, образуя единство. Великий немецкий философ Г. Гегель (1770-1831) дал определение гармонии как метод сопряжения «противоположностей»: «Гармония – соотношение качественных различий, взятых как единое целое (отмечено нами. В.Ц.) и представляющее собой суть явления» [по 86]. В современной науке идея гармонии «противоположностей» получила дальнейшее развитие. По мнению белорусского философа Э.М. Сороко, «великая карта оптимальных состояний природы, согласно которой та создает свои порядки, написана языком противоположностей, контрарностей, противодействий» [151, с. 101]. В настоящее время установлено: «противоположности» пронизывают все основные физические объекты в микро-, макро- и гипермирах Природы. Мир устроен так, что любое явление живой и неживой Природы обязательно имеет свою «противоположность». Гармония «противоположностей» является необходимым условием устойчивости систем. Отметим, выявление гармонии «противоположностей» в сердечных циклах, процессах и структурах составляет одну из главных задач нашей книги.

Древнегреческое учение о гармонии и «противоположностях» неразрывно связано с концепцией Числа. «Противоположности», числа и их отношения у греков играли первостепенную роль в понимании и объяснении окружающего мира, его структуры и механизмов развития. Как полагали пифагорейцы, «Бог – это единство, а мир - множество и состоит из противоположностей. То, что приводит противоположности к единству и соединяет все в космосе, есть гармония. Гармония является божественной и заключается в числовых отношениях» (отмечено нами. В.Ц.) [по 28, с. 129]. Таким образом, гармония «противоположностей», по представлению греков, может предстать в качестве объекта математического исследования. Особенность такого исследования состоит в том, что математический подход «фиксирует внимание на количественной стороне дела и безразличен (отмечено нами. В.Ц.) к качественному своеобразию частей, вступающих в гармоническое соответствие» [212, с. 15]. Например, универсальное математическое соотношение - золотая пропорция - «присутствует» во множестве объектов и живой, и неживой природы, а также в шедеврах творческой мысли человека: музыке, архитектуре, живописи, литературе [30]. Эта пропорция, обладающая многими уникальными свойствами, имеет ключевое значение в предпринятом нами исследовании.

По современному представлению [36], «Золотая пропорция – это равенство отношений целого a к большему b и большего b к меньшему с» (a:b=b:c). (Например, для целого а=1 золотая пропорция имеет место, если b=0,618 и c=0,382; при этом 1:0,618=0,618:0,382 = 1,6180339…). Деление целого по золотой пропорции с давних пор известно как деление в среднем и крайнем отношениях или золотое сечение. Универсальное число 1,6180339… получило обозначение Ф в честь древнегреческого зодчего Фидия (490-430 до н. э.), который часто его использовал при строительстве храмов и скульптур. (В практических расчетах обычно используют Ф=1,618.) Важнейшую роль золотого сечения в гармонизации объектов природы отмечали величайшие философы Древней Греции Пифагор и Платон. «Противоположности» в этой пропорции имеют меру математического разрешения, поскольку известен критерий деления целого (Ф=1,62). Для нас имеет большое значение то, что в структуре золотой пропорции представлено единство пары «противоположностей» («больше» - меньше»). Как будет показано нами в этой книге (см. 2-4 главы), эта пара «противоположностей» + целое, соединенные в золотой пропорции, имеют широкое представление во множестве сердечных систем.

Золотое сечение лежит в основе «Математики Гармонии» – весьма перспективного направления в современной математике. Математика Гармонии – это возрождение древнегреческой математической школы Пифагора, Платона, Евклида. «Золотое» направление имеет тесные связи с естествознанием, в частности, с биологией, ботаникой, медициной, информатикой, синергетикой, теоретической физикой. Необходимо отметить удивительное постоянство, с каким проявляется золотое сечение практически на всех уровнях организации природы (генетический код, фуллерены, квазикристаллы, филлотаксисные структуры, морфология человека, сердечные циклы, форма Земли, «золотая» спираль Галактики и т.д.). Особые свойства золотого сечения, по мнению Э.М. Сороко [51, с. 83], «позволяют возвести это…математическое сокровище в разряд инвариантных сущностей гармонии». Объяснения причины столь широкого «распространения» золотого сечения в живой и неживой природе пока не существует. Эта загадка все еще остается нерешенной. Следует ответить лишь на «маленький» вопрос: «Почему Природа так часто «использует» золотое сечение?» Биологам, в частности, для ответа на эту «загадку» необходимо выявить универсальный критерий гармонии для множества живых систем, «использующих» золотое сечение.

Гармония требует длительного и всестороннего изучения объекта. Очевидно, что перед исследователями при изучении всякой системы организма неизбежно встают непростые вопросы: «Для чего?», «Как?», «Почему именно так, а не иначе?». Ответ на первый вопрос состоит в установлении функции системы, ответом на второй является изучение ее структуры и организации, ответ на третий – выявление гармонии в изучаемом объекте. На исключительную важность решения последнего вопроса указывал великий русский ученый К.А. Тимирязев (1843-1920): «Для полного познания сущности объекта недостаточно ответить на вопрос, как он устроен, необходимо также знать, почему он устроен именно так? (отмечено нами. В. Ц.)». В нашей книге на основе анализа «золотых» «противоположностей» в сердечных циклах и структурах человека и млекопитающих предпринята попытка хотя бы частично ответить на этот вопрос.

Любой объект природы, воздействующий на наши органы чувств, всегда каким-либо образом организован во времени и пространстве. Каждая живая система имеет свою внутреннюю логику как следствие самоорганизации ее элементов. Отметим, самоорганизация как аспект деятельности биосистем всегда привлекала внимание крупных ученых. Лауреат Нобелевской премии Н. Винер, отмечая важность проблемы организации, писал: «Главные проблемы биологии…связаны с системами и их организацией (отмечено нами. В.Ц.) во времени и пространстве» [35, с. 43]. По мнению известного биолога Дж. Нидхэма, «Биологический порядок и организация не являются аксиоматическими категориями, а, напротив, предъявляют к исследователям требование фундаментальной (отмечено нами. В.Ц.) важности - дать этим понятиям научное истолкование» [299, p. 214]. Добавим к этому, предварительное изучение организации живого объекта является непременным условием раскрытия гармонии последнего. Выявлению организации, а затем и гармонии, живых систем должен предшествовать ряд обязательных условий. Прежде всего, необходимо иметь достаточный объем экспериментально полученных результатов, чтобы иметь представление об особенностях организации частей изучаемого объекта. В связи с этим вспомним, великий математик А. Пуанкаре считал, что «опыт есть единственный источник истины» [по 174, с. 273]. Он же подчеркивал невозможность довольствоваться в научном познании только опытом и обосновывал необходимость теоретических обобщений. Естественно, разрозненные факты сами по себе не представляют большой ценности без их интеграции и синтеза. Они приобретают значение, только будучи связанными в рамках единого целого какой-либо теорией. Обратимся, например, к медицине. В результате многолетнего труда армии ученых в этой области получены горы экспериментальных данных. Отмечая создавшееся положение, лауреат Нобелевской премии Г. Селье (1907-1982) еще в прошлом веке писал о «настоятельной необходимости в сведении воедино огромного количества данных, публикуемых в медицинских журналах» [143, с. 34]. «Но, - с сожаленьем отмечал далее Селье, - чем больше публикаций, тем меньше людей, желающих заняться такой интеграцией данных». Сходная в той или иной мере ситуация сложилась не только в медицине, но и в других науках о живом. К большому сожаленью, необходимо отметить, что до сих пор в биологических науках аспекту организации не уделяется должного внимания. Организация живых объектов многими биологами все еще воспринимается как нечто аксиоматическое, не представляющее интереса для изучения. По-прежнему на первом плане – все большая детализация структуры систем и протекающих в них процессов. В результате такого «измельчения» от исследователя ускользают законы организации сложного объекта. Дополнительная трудность изучения организации живых систем связана с их огромной сложностью и большим разнообразием. Отметим, даже простейшие организмы имеют неизмеримо более сложное строение, чем любая система, созданная разумом человека. Поэтому чаще всего исследование сложных систем имеет «мозаичный» характер. Мир живой природы удивительно многообразен. Вместе с тем, неизменно наблюдаемое совершенство и подобие множества биосистем различного назначения позволяет высказать предположение о существовании универсальных критериев их организации. На пути выявления этих критериев существуют большие трудности. Единство различных разделов биологии и медицины разорвано на куски «вавилонской башней» профессиональных языков. Глубокая специализация, повсеместное применение компьютеров и рейтинговая оценка по числу публикаций в престижных специализированных журналах итогов деятельности ученых, в конечном счете, приводят к тому, что профессионалы из разных областей биологии и медицины часто не в состоянии понять друг друга, да и не очень желают этого. Добавим к этому, биологи и медики, стремящиеся использовать математику, часто не имеют необходимой математической подготовки, математики же не понимают глубоко сущность «системных» биологических проблем. Необходимо, чтобы исследователь живых систем имел достаточно высокую математическую и медико-биологическую квалификацию. Такое взаимное «проникновение» все еще является, к сожаленью, редким случаем. В России, по нашему мнению, наиболее яркими представителями такого рода исследователей являются А.Л. Чижевский, А.А. Любищев, Ю.А. Урманцев.

По нашему глубокому убеждению, поиск универсального критерия гармонии возможен лишь в рамках системного подхода к исследуемому объекту. В качестве метода системный подход позволяет объединить функцию, структуру, организацию, а затем и гармонию, живых систем с некоторых общих позиций. Естественно, что системный подход находит благоприятную почву в биологии и медицине. Для нас наибольший теоретический интерес представляет вариант системного подхода – общая теория систем (ОТС) Ю.А. Урманцева [180, 181]. Разработанный Ю.А.Урманцевым вариант ОТС связан с понятиями «объект» и «объект-система». За «объект» признается любой предмет мысли, т.е. предметы объективной и субъективной реальности, и не только вещи, но также качества, свойства, отношения, процессы и т.д. «Объект-система» - это единство, созданное определенного сорта «первичными» элементами + связывающими их в целое отношениями (в частном случае, взаимодействиями) + ограничивающими эти отношения условиями (законом композиции). В каждой объект-системе необходимо выделить следующие аспекты: 1) первичные элементы, рассматриваемые на данном уровне исследования как неделимые; 2) отношения единства между этими элементами и 3) законы композиции (организации), определяющие границы этих отношений. (В качестве объект-системы можно представить, например, атом. Нейтроны, протоны и электроны являются «первичными» элементами в атоме, в качестве системообразующего отношения - определенного рода физические взаимодействия между ними, в качестве закона композиции - законы атомной физики.) Понятие о законе композиции (организации), впервые введенное Ю.А.Урманцевым в определение системы, позволяет представить живую систему как закономерный, упорядоченный, неслучайный набор объектов. Системный подход по Урманцеву позволяет произвести анализ выбранного живого объекта в естественном единстве его функции, структуры и организации. Такой подход позволил нам найти путь к выявлению гармонии «противоположностей» в отдельных сердечных объектах и сердце в целом.

Живых систем, экспериментально изученных достаточно глубоко и всесторонне, пока еще совсем немного. Выбор нами сердца человека и млекопитающих в качестве объекта, пригодного для выявления универсальных критериев гармонии живых систем, не случаен. К настоящему времени этот орган достаточно хорошо изучен как по «вертикали» (иерархия систем), так и по «горизонтали» (множество параметров деятельности). Повышенный интерес в науке к сердечной тематике, начиная со второй половины 20 века и до наших дней, обусловлен широким распространением ишемической болезни сердца. Это заболевание пожилых людей все более «молодеет» и принимает в наиболее развитых странах характер эпидемии. Одним из итогов международной кооперации ученых, занятых борьбой с этой «чумой» прошедшего и 21 века, явилось накопление огромного объема экспериментальных данных, отнесенных к самым различным сторонам структуры сердца (особенно к системе обеспечения миокарда кровью и кислородом). Совокупность этих данных представляет большой интерес для специалистов, занимающихся проблемами теоретической биологии и медицины. Можно сказать, сердце - подходящее «поле поиска» принципов гармонии, которые, возможно, могут оказаться универсальными для всех живых систем независимо от их сложности и назначения.

В свое время автором был произведен системный анализ огромного объема «сердечных» публикаций отечественных и зарубежных ученых. В итоге впервые был установлен универсальный критерий сопряжения (гармонии) множества «простых» сердечных систем в отдельной «сложной» кардиосистеме – принцип оптимального вхождения [193]. Суть этого принципа заключается в следующем: «Каждая из «простых» сердечных систем, совместно образующих «сложную» кардиосистему, включена в последнюю оптимальным образом, вследствие чего сложная система исполняет свою функцию с минимальными затратами энергии и строительного материала». (Обозначения «простая» и «сложная» условны. «Простая» система по отношению к своим «простым» системам предстает в качестве «сложной»; эта же система, рассматриваемая в составе более сложной системы становится «простой».) Отметим важное обстоятельство: в принципе оптимального вхождения представлено не только оптимальное единство функции, структуры и организации «сложных» сердечных объектов, но также и оптимальная гармония последних. Связь принципа оптимального вхождения и гармонии «противоположностей» вытекает из следующего феномена. В каждой сердечной системе обязательно «присутствует» пара «противоположностей: «больше» - «меньше». Эти «противоположности» имеют место потому, что любой параметр (система по Ю.А. Урманцеву) имеет определенный диапазон значений, в пределах которого может обеспечиваться нормальная деятельность сердца. Оптимальная «рабочая» величина рассматриваемого параметра разделяет диапазон возможных значений на два «противоположных» участка: участок «положительных» и участок «отрицательных» приращений. «Противоположные» участки («простые» системы) в соответствии с принципом оптимального вхождения оптимальным образом входят в целое – диапазон возможных значений («сложную» систему), чем обусловливают оптимальную гармонию последней. Отметим, эта «сложная» сердечная система совместно с другими «сложными», образует, в свою очередь, еще более сложную кардиосистему, которая также имеет свои оптимальные «противоположности» и т. д. В этой книге нами показано, что оптимальность «противоположностей» сохраняется для всякой последовательности систем возрастающей сложности, объединенных функциональной зависимостью. Можно сказать, принцип оптимального вхождения имеет в своей основе оптимальное сопряжение (гармонию) «противоположностей» во всех сердечных системах любой сложности. В каждой сердечной системе соотношение оптимальных «противоположностей» равняется определенному числу; таким числом во многих системах является золотое число 1,618. Феномен оптимального сопряжения «противоположностей» в сердечных системах обстоятельно представлен нами в 2, 3 и 4 главах данной книги.

Нашей задачей в данной книге является показать «присутствие» энерго-вещественной оптимальности, гармонии «противоположностей» и «особых» чисел в сердечных системах независимо от их сложности и назначения.

Книга состоит из Введения, 4 глав и Заключения.

1 глава является своего рода вступлением к 2-4 главам. Прежде, чем перейти к конкретному биологическому объекту – сердцу человека и млекопитающих, недостаточно подготовленный читатель получает в этой главе общее представление о Математике Гармонии, пропорции золотого сечения и числах ряда Фибоначчи, системном подходе, «простоте» и оптимальности Природы. Показано «присутствие» принципа энергооптимальности в физике и биологии. Представлена Математика Гармонии – новое направление в современной математике, имеющее своим истоком труды древнегреческих ученых Пифагора, Платона и Евклида. «Золотое» число Ф=1,618 является основанием этой математики. Представлено множество примеров «присутствия» золотой пропорции и чисел Фибоначчи во многих объектах живой и косной природы, а также многих шедеврах творческой мысли человека.

В 2 главе рассмотрена «золотая» гармония «противоположностей» в структурах сердечных циклов (ССЦ) важнейших параметров сердца, а также ССЦ основных параметров архитектоники и гемодинамики микрососудистого и капиллярного участков коронарного русла. Установлены обобщенные законы композиции «пространств» этих ССЦ в условиях покоя и физической нагрузки. Представлены золотые и другие «особые» числа, обусловливающие энергооптимальную структуру рассматриваемых «пространств» ССЦ.

В 3 главе выполнен анализ особенностей конструкции докапиллярного кислороднесущего русла сердца с учетом гармонии «противоположностей». Произведена последовательная «сборка» энергооптимальных кислороднесущих систем по мере их усложнения. Произведен анализ преимуществ бифуркационного ветвления сосудов. Показана оптимальная энерго-вещественная взаимосвязь на этом участке между гемодинамикой, конструкцией предкапиллярных микрососудов и «ценой» транспорта потребляемого кислорода. Показано «присутствие» золотого сечения и чисел Фибоначчи на обменном участке.

В 4 главе показано оптимальное сопряжение параметров гемодинамики, архитектоники и кислородного обеспечения на капиллярном участке сердца, а также дыхательных пигментов эритроцитов и кардиомиоцитов. Адекватная деятельность кардиомиоцитов обеспечивается при минимальном объеме их субструктурных компонентов и минимальном потреблении энергии и кислорода. Показано «присутствие» золотого сечения и чисел Фибоначчи в структуре кардиомиоцитов.

В заключение заметим, «математическая» гармония сердечных систем представлена значительным количеством формул, внешне довольно простых. Читатель в случае затруднений математические выкладки может пропускать и довольствоваться текстом и выводами.

Использованные в книге экспериментальные данные относятся к здоровым людям и животным репродуктивного возраста, пребывавших во время экспериментов в среде с нормальными параметрами обитания (нормальный состав, влажность и давление вдыхаемого воздуха, нормотермия, нормальный состав пищи, отсутствие стрессовых ситуаций и т. д.). Для анализа использовались среднестатистические значения параметров, погрешность измерения которых не превышала ±10%.

Автор выражает большую благодарность за обсуждение выдвинутых положений ответственному редактору книги д. т. н., проф. И.И. Свентицкому, рецензенту д. мед. н., проф. В.А. Глотову, д. филос. н., проф. Ю.А. Урманцеву, д. т. н., проф. А.П. Стахову (Канада), д. филос. н., проф. Э.М. Сороко (Белоруссия), д. т. н., проф. О.Б. Балакшину, проф. Денешу Надю (Венгрия), проф. Скотту Олсену (США), д. мед. н., проф. А.Г. Субботе, д. б. н., проф. В.В. Петрашову, д.т.н. В.Л. Владимирову (ФРГ), д. филос. н., проф. А.В. Волошинову, к. ф.-м. н. А.С. Харитонову, а также д. б. н. Ю.Г. Каминскому за неизменный интерес к данной работе и моральную поддержку.

Автор выражает благодарность Е.В. Бескаравайной за помощь в техническом оформлении книги.

Глава 1

МАТЕМАТИКА ГАРМОНИИ, ЗОЛОТОЕ СЕЧЕНИЕ И ЭНЕРГООПТИМАЛЬНОСТЬ

1.1. Пифагорейцы – основоположники Математики Гармонии

Первой научной школой, предложившей свой вариант математического плана строения Вселенной, были пифагорейцы. Выдающийся математик и биолог Д`Арси Томпсон, обобщая математическую основу учения пифагорейцев, писал: «Гармония Природы является в Форме и Числе; и сердце, и душа всей поэзии Натурфилософии воплощена в понятии математической красоты…Не только движения небесных тел определяются наблюдением и разъясняются математикой, но и все остальное может быть выражено числом и определено естественными законами. Это – учение Платона и Пифагора и завещание человечеству греческой мудрости» [по 10, с. 80]. Представителями греческой школы были сформулированы два тезиса, значимость которых подтвердило все последующее развитие науки. Сущность этих тезисов состояла в следующем:

1) основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики,

2) объединяющим началом всех вещей является числовые отношения, которые выражают гармонию и порядок Природы.

В античной науке возникли два пути развития математики [162]. Первый путь был основан на проблеме счета и проблеме измерения. В этот период в математике было сделано два ключевых открытия. Позиционный принцип представления чисел, открытый вавилонскими математиками, был использован во всех известных системах исчисления, включая вавилонскую 60-ричную, десятичную и двоичную. Развитие этого направления привело к формированию концепции натурального числа и созданию теории чисел, первой фундаментальной теории математики. Несоизмеримые отрезки, открытые пифагорейцами, привели к открытию иррациональных чисел и созданию теории измерений, второй фундаментальной теории математики. В конечном итоге, натуральные и иррациональные числа и стали теми фундаментальными понятиями, которые были положены в основу всех математических теорий «классической» математики (теория чисел, алгебра, геометрия, дифференциальное и интегральное исчисления). Основные «элементарные функции» классической математики известны каждому со школьных времен (тригонометрические, экспоненциальная, логарифмическая, гиперболическая функции). Все они основаны на «главных математических константах»: - тригонометрические на числе π=3,1415…, экспоненциальная, логарифмическая и гиперболическая функции на числе е=2,718… (основание натуральных логарифмов).

Второй путь представлен тем, что параллельно с «классической» математикой в античной науке начала развиваться еще одна математическая теория - «Математика Гармонии». Эта теория в своем источнике имеет идеи древнегреческих мыслителей и математиков Пифагора и Платона. Большая заслуга в открытии этого направления принадлежит представителю школы Платона древнегреческому математику Евклиду (325-265 до н. э.). Евклид создал «Начала» - самое значительное математическое сочинение античной эпохи. Это произведение содержит основы античной математики: элементарную геометрию и теорию чисел, алгебру, теорию пропорций и отношений, теорию иррациональностей, методы определения площадей и объемов и др. Евклид подвел в этом произведении итог 300-летнему развитию греческой математики. Древнегреческий философ и математик Прокл Диадох (412-485) высказал гипотезу, что главная цель создания «Начал» состояла в том, чтобы изложить построение «Платоновых тел» (см. раздел 1.2). «Ключевым» открытием в этой области является деление отрезка в крайнем и среднем отношении (золотое сечение), введенное Евклидом для того, чтобы дать геометрическую теорию додекаэдра – одного из важнейших Платоновых тел. «Начала» следует рассматривать как «первую попытку создать Математическую теорию гармонии Мирозданья», которая ассоциировалась в древнегреческой науке с Платоновыми телами и золотым сечением. От этой проблемы, по мнению А.П. Стахова [159], берет свое начало «Математика Гармонии» как новое междисциплинарное направление и «золотая» парадигма современной науки. Таким образом, начиная с Евклида, возникло новое междисциплинарное направление, которое продолжается и активно развивается в наше время [159, 161, 162]. Это направление математики имеет тесные связи с естествознанием, в частности, с теоретической физикой, ботаникой, генетикой, биологией, информатикой, синергетикой. Термин «Математика Гармонии» (the mathematics of harmony) был введен в конце 20 века в Оксфордском философском справочнике для обозначения математического учения о природе, созданного древними греками.

Современное учение о гармонии основывается на следующих важнейших положениях [157]:

1. Для того, чтобы иерархическая система была устойчивой, каждый ее элемент на любом уровне ее организации должен быть «гармоничным» - это главное положение научной парадигмы, восходящей к Пифагору и Платону.

2. Не всякое сочетание создает «гармоническую», то есть, «устойчивую» структуру. Для этого каждый элемент должен быть образован по «законам» гармонии.

3. «Математическая теория чисел» или «Математика Гармонии», направленная на поиск «Математических законов Гармонии», носит универсальный характер, то есть, приложима ко всем структурам природы на любых уровнях ее организации.

Математика Гармонии «фиксирует внимание на количественной (отмечено нами. В.Ц.) стороне дела и безразлична к качественному своеобразию частей, вступающих в гармоническое соответствие» [212, с. 15]. Это направление математики следует рассматривать как науку о моделях гармонических процессов и структур, реально существующих в окружающем нас мире. «Математика Гармонии» может стать, - пишет А.П. Стахов [159], - основой «Науки о Гармонии Систем», важного междисциплинарного направления современной науки». Отметим, что используемый нами в этой книге системный подход к исследованию сердца млекопитающих теснейшим образом связан со структурной гармонией систем.

Уже в древности теоретическая основа гармонии была связана с числами и их отношениями. Древнегреческому философу и геометру Пифагору и его ученикам приписываются выражения: «Все вещи - суть числа», «Бог положил числа в основу мирового порядка», «Мир создан в подражание числам». Пифагор и пифагорейцы считали, что числа обладают таинственными, мистическими силами и они суть божественные существа. Число, рассматриваемое со всех этих сторон, есть сущность всего существующего, высшая объективная реальность. Числам принадлежит большая реальность, чем конкретным вещам, т. к. последние суть только проявления чисел, это – лишь внешняя сторона чисел, которая одна видна непосвященным, не постигающим внутренней сущности вещей. Следует отметить, «пристрастие» пифагорейцев к числам во многом было связано с мистикой. «Пифагорейцы предавались математике, как чему-то вроде религиозного созерцания, дабы приблизиться к божеству» [28, c. 146]. Пифагорейцы считали, что числа – это одновременно и разумная, и мистическая, и материальная основа вещей. Некоторые числа пифагорейцы считали священными. Например, число 2 олицетворяло женское начало, число 3 – мужское. Число 5=2+3 выражало брак - единство женского и мужского - и почиталось как священное. Кроме того, число 5 совмещало в себе симметричное начало (5=2+1+2) и асимметричное (5=2+3). Число 6 олицетворяло совершенство, ибо оно равно сумме всех делителей: 6=1+2+3. Числа 1, 2, 3, 4 имели у пифагорейцев особое значение. Сумма этих чисел, равная 10 (пифагорская четверица). Четверка образует целое, т.е. видимое и невидимое, т.е. выражает собою «Все». Пифагорейцы давали клятву священной декадой. Наряду с четверицей наиболее чтимым было число 36 (тетраксис), служившее символом всей Вселенной. Число 36 равно сумме первых четырех четных и четырех нечетных: 36=2+4+6+8+1+3+5+7. Клятва числом 36 считалась у пифагорейцев самой страшной. Пифагору приписывают изречение: «Познать мир – значит познать управляющие им числа». В наши дни не подлежит сомнению, что пифагорейцы были не правы, когда отождествляли мир вещей и чисел, но именно они сумели нащупать в мире вещей мир чисел, т.е. нечто фундаментальное и до сих пор во многом загадочное. Положение пифагорейцев о том, что числа правят миром, имеет мистический характер, что является причиной прохладного отношения к математике древних значительной части представителей классической науки нашего времени. Однако вспомним, что Иоганн Гёте, который был не только великим поэтом и мыслителем, но и крупным натуралистом, высказал в свое время глубокую мысль: «Числа не управляют миром, но показывают, как управляется мир», чем отделил пифагорейскую мудрость от мистики.

Большое значение пифагорейцы приписывали числам в деле познания. Пифагореец Филолай (вторая половина 5 в. до н.э.) утверждал: «Число есть основание оформленности и познаваемости всего сущего. Все познаваемое имеет число. Ибо без него невозможно ничего ни понять, ни познать». С помощью чисел пифагорейцы не просто решали практические задачи, а пытались объяснить природу всего сущего. Они стремились постигнуть сущность чисел и числовых отношений, ибо через нее надеялись понять сущность мироздания. Платон по этому поводу писал: «Мы никогда не стали бы разумными, если бы исключили число из человеческой природы» [по 40, с. 6]. Таким образом, в Древней Греции возникла первая в истории «попытка осмыслить число как миросозидающий и смыслообразующий элемент» [205]. Пифагор и его ученики заложили основы Математической Гармонии. С этой точки зрения «Начала» Евклида были первой попыткой свести воедино имеющиеся к тому времени знания, первым подходом к созданию «математической» теории Гармонии, что было главной идеей греческой науки. Пифагорейцы первыми возвысили математику до ранее неведомого ей ранга: числа и числовые отношения стали рассматриваться ими как ключ к пониманию Вселенной и ее структуры. Они впервые пришли к убеждению, что «книга природы написана на языке математики», как спустя почти два тысячелетия выразил эту мысль Галилей.

Особое внимание Пифагор и его ученики уделяли пентаграмме – пятиконечной звезде, образованной диагоналями правильного пятиугольника. Пятиконечная звезда известна около 3000 лет; ее первые изображения донесли до нас вавилонские глиняные таблички. Как полагают, звездчатый пятиугольник из Древней Вавилонии в Грецию привез Пифагор [28]. В пентаграмме пифагорейцы обнаружили золотое сечение, которое в то время называлось «сечением в среднем и крайнем отношении». Звезда буквально «напичкана» золотыми сечениями, в ней установлено более 200 «золотых» соотношений. Пентаграмма считалась у пифагорейцев священной фигурой, символом гармоничной жизни и здоровья. Более того, Пифагор и его ученики сделали пентаграмму тайным опознавательным знаком своего сообщества.

Современная философия и методология науки в целом очень высоко оценивает деятельность Пифагора и его последователей, их вклад в развитие человеческого познания. По мнению выдающегося русского философа А.Ф. Лосева (1893-1988), пифагорейская философия чисел, исследования пифагорейцев в области математики, астрономии и музыки «это - величайший вклад в сокровищницу мировой философии и науки, потому что возникновение математического естествознания в новое время философски было связано с идеями пифагореизма» [102, с. 260]. «Я не знаю ни одного человека, - писал английский математик и философ Б. Рассел (1872-1970), - который оказал бы такое влияние на человеческое мышление, как Пифагор» [127, с. 42]. Величайшая заслуга Пифагора состоит в том, что он впервые ввел в математику метод доказательства, благодаря чему математика превратилась в самостоятельную науку. Многие ученые считают Пифагора родоначальником чистой математики, поскольку Пифагор сделал первый шаг к сплошной математизации наших знаний. Учение пифагорейцев стало самым мощным в истории познания фактором, наложившим сильнейший отпечаток на все дальнейшее развитие европейской философии и, в первую очередь, математики. «Математические теории позволили обнаружить порядок и план повсюду в природе, где их только можно было найти» [79, с. 350]. Об этом же пишет Н. Винер (1894-1964): «Высшее назначение математики…состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает» [по 41, с. 47].

Древнегреческие философы впервые объединили Число и Гармонию. Теория Числа как единого организующего принципа Мироздания является стержнем всей философской системы Пифагора. Особенно велик вклад пифагорейцев в теорию пропорций (в том числе и золотого сечения), на которых основана вся античная наука и культура. Среди современных теоретиков, занимающихся проблемой гармонии, структуры и организации, возрастает интерес к «золотой» пропорции и «золотому» числу Ф=1,618. В пропорции, связанной с золотым числом, представлено неравенство сопрягающихся элементов целого, соединенных законом подобия, которое выражает заключенную в золотом сечении меру симметрии и асимметрии. В связи с этим, Э.М. Сороко высказал мнение, что «сочетание симметрии и асимметрии в определенной пропорции и есть гармония» [151]. Отметим, золотая пропорция обладает уникальным комплексом свойств: мультипликативности, аддитивности и симметрии подобия. Это неповторимое по гибкости сочетание свойств отображает особенности золотой пропорции. Особые свойства золотого сечения позволяют возвести это, говоря словами Кеплера, «математическое сокровище» в разряд инвариантных сущностей гармонии. «С точки зрения Платона, да и вообще с точки зрения всей античной космологии, - писал А.Ф. Лосев, - мир представляет некое пропорциональное целое, подчиняющееся закону гармонического деления – золотого сечения». Он же считал, что «закон золотого сечения должен быть диалектической необходимостью» [101, с. 412]. В наше время Математика Гармонии является развитием и обобщением тысячелетних исследований в области теории золотого сечения, которая начала создаваться в Древней Греции. Ее главная цель – ввести в современную науку золотое сечение в качестве фундаментального понятия современной науки.

Большое значение в развитии Математики Гармонии имело то, что пифагорейцы обратили внимание на правильные многогранники. Существуют пять правильных многогранников: четырехгранник (тетраэдр), шестигранник (куб), восьмигранник (октаэдр), двенадцатигранник (додекаэдр) и двадцатигранник (икосаэдр). Все правильные многогранники были известны пифагорейцам и получили в дальнейшем название Платоновых тел по имени Платона, впервые их систематически описавшим. Каждое из этих тел, по представлению Платона, символизировало одно из пяти «начал» или «стихий»: тетраэдр - тело огня, октаэдр - тело воздуха, гексаэдр (куб) - тело земли, икосаэдр - тело воды, додекаэдр - тело мира (вселенской души, эфира или разума). По мнению Э.М. Сороко [150], Евклид «создавал «Начала»…, чтобы дать полную систематизированную теорию построения пяти «Платоновых тел», попутно осветив новейшие достижения математики». Евклидом впервые была показана возможность построения всех правильных многогранников на основе деления отрезка в среднем и крайнем отношении (т. е. с использованием золотого сечения). Пятиугольники присутствуют в двух из этих многогранников. Это додекаэдр, имеющий 12 пятиугольных граней и икосаэдр, имеющий 20 треугольных граней. Если в додекаэдре пятиугольники, носители золотого сечения, являются гранями, то в икосаэдре они образуются при соединении пяти треугольников в одной вершине. Сумма граней и вершин у додекадра и икосаэдра одинакова (равна 32); эти многогранники могут легко переходить друг в друга. Геометрические отношения между додекаэдром и икосаэдром также определяются золотым сечением [90]. Роль этих совершенных фигур, основанных на золотом сечении, в развитии науки столь велика, что правомерно говорить о том, что в трудах Платона возникла «икосаэдро-додекадрическая доктрина», которая красной нитью проходит через всю науку. Отметим, что еще Сократ высказывал предположение, что Земля имеет форму додекаэдра. В 17 веке И. Кеплер, используя тела Платона, построил оригинальную геометрическую модель Солнечной системы. Икосаэдр, по мнению выдающегося немецкого математика Ф. Клейна, является главной геометрической фигурой математики [80]. В наше время установлено «присутствие» всех Платоновых тел в древнейшей фигуре сакральной геометрии - «Цветке Жизни» [106].

Столь близкая связь между додекаэдром и икосаэдром, возможность трансформации одного в другое играет, по мнению многих, большую роль в живой природе. Установлено, что в ходе зародышевого развития многоклеточных животных организмов, называемого гаструляцией, вначале образуется тетраэдр из четырёх клеток, потом октаэдр, куб, а потом икосаэдр и додекаэдр, словом все пять платоновых тел, притом в строгой последовательности. Не менее интересны утверждения, касающиеся структуры молекулы ДНК. Поворачивая куб определённым образом на «золотой» угол в 72^о, можно получить икосаэдр, составляющий, как мы уже знаем, дуальную пару с додекаэдром. Получается, что в построенной по принципу двустороннего соответствия двойной нити спирали ДНК за икосаэдром следует додекаэдр, затем снова икосаэдр, и так далее. Таким образом, молекула ДНК геометрически представляет собой полученное вращением куба чередование икосаэдров и додекаэдров. А.Г. Волохонский [39] установил соответствие общей структуры генетического кода, ряда биноминального разложения 2 и икосаэдра. Английский биохимик Дж. Кендрью показал, что пространственная конфигурация молекулы миоглобина имеет форму икосаэдра [89]. Им же было установлено, что вирусы, состоящие из белка и РНК, также представляют собою правильные икосаэдры. Можно добавить к этому, что среди представителей живой природы чаще всего встречается симметрия 5-го порядка, невозможная для затвердевшего, окристализованного, «мертвого» вещества. Известна пятерная симметрия медуз, осьминогов, морских звезд, многих цветов, внутреннего строения сердцевины яблока, расположения листьев и т.д. О сущности этого явления оригинальную идею высказал академик Н.В. Белов: «Можно подумать, что пятерная симметрия является у мелких организмов своеобразным инструментом борьбы за существование, страховкой против окаменения, против кристаллизации, первым шагом которой была бы их «поимка» решеткой» [12, с. 41].

Отметим, в современной науке, как продолжение традиций школы Пифагора, возрождается интерес к «особым» числам, представленным во многих объектах природы. Как пишет Ю.А. Урманцев, «Числа выступают на передний план в самых «горячих» точках науки: то при изучении распределения планет в Солнечной системе, то при объяснении сущности кода наследственности, то при выводе фундаментальных инвариантов в теоретической физике, то при определении периодической природы музыкального ряда и таблицы Менделеева» [180, с. 16-17]. Одним из таких чисел является безразмерная величина a=q²/ħc = 1/137,03…, включающая в себя мировые константы с - скорость света, q - заряд электрона, ħ =h/2p, где h - постоянная Планка. Эйнштейн и Планк, как считает Г.Б. Аракелян [2], были первыми, кто обратил внимание на безразмерную величину a=q²/ħc. Величина a получила обозначение постоянной тонкой структуры. Известно, что Эйнштейн пытался, хотя и безуспешно, установить связь между величинами q, ħ и c. Величина a=1/137,03 обеспечивает стабильное существование материи, в том числе и живой. В последние годы в физике установлено, что набор мировых констант, таких как скорость света, постоянная гравитации и т.д., обладает удивительным свойством. Даже ничтожные их изменения, порядка малых долей процента, привели бы к такому изменению характера мирового процесса самоорганизации, который исключил бы возможность появления во Вселенной достаточно стабильных структур, таких, например, как Солнечная система и, в конечном счете, возникновения жизни на Земле. М.А. Марутаевым [105] на основе разработанной им качественной симметрии была показана связь золотого числа F=1,618 с фундаментальным числом b=a^-1»137. «Присутствие» ключевой величины Математики Гармонии – золотого числа – установлено во многих системах теоретической физики, химии, ботаники, генетики, биологии, медицины, синергетики и других наук.

Основные классы элементарных функций «классической» математики основаны на «особых» математических константах: тригонометрические - на числе p, экспоненциальная, логарифмическая и гиперболические функции – на числе е. «Особые» числа e=2,718… и p=3,14…1 в различных сочетаниях входят в основные уравнения физики. Золотое число Ф=1,618… также становится особым числом. Ситуация такова, что Природа словно «благоволит» к этим числам, равнодушно «отвергая» остальные. Появление в науке «особых» чисел является неизбежным следствием применения в ней аппарата чистой математики в качестве универсального средства для количественного описания явлений природы. Однако, «весь вопрос, - как пишет Г.Б. Аракелян [2, c. 133], - ...в том, почему при описании наиболее фундаментальных закономерностей появляются именно эти (отмечено нами. В.Ц.), а не другие числа?».

1.2. Математика Гармонии и «золотое» число Ф

Математическое представление гармонии, как правило, выражается в виде определенных числовых пропорций. Древние понимали пропорцию следующим образом: «Две части или две величины не могут быть ...связаны между собой без посредства третьей....Достигается это...пропорцией (аналогией), в которой из трех чисел..., среднее так относится ко второму, как первое к среднему, а также второе к среднему, как среднее к первому» [121, с. 435]. Пропорция такого рода получила у древних название «деление в среднем и крайнем отношении», а в дальнейшем – «золотая пропорция». В приведенном высказывании Платон четко указал на «золотую пропорцию», хотя и не использовал это название. Под пропорцией здесь понимается отношение частей целого между собой и с целым; очевидна особая роль среднего пропорционального (Ф=1,618…). Важная особенность золотой пропорции заключается в том, что это результат согласования двух соотношений, поэтому необходимо иметь три элемента в отличие от отношения, где достаточно двух: да – нет, хорошо – плохо, порядок – беспорядок и т.д. Среднее пропорциональное содержит в себе «качественное обобщение, т.к. оно выражается одним числом, а не множеством» (отмечено нами. В.Ц.) [105, с. 162]. Таким образом, отдельные конкретные числа и отношения способны выражать не только количество, но и «качество». Золотое сечение является самым известным примером «качества», представленного в отношении.

Учение о золотом сечении возникло в результате тщательного исследования природы чисел. Считается, что деление отрезка в среднем и крайнем отношении впервые было осуществлено великим философом и геометром Древней Греции Пифагором (570-500 до н.э.). Возможно, по мнению Вардена [28], Пифагор позаимствовал деление отрезка в среднем и крайнем отношении у древних египтян и вавилонян. В форме алгебраического выражения это соотношение можно представить следующим образом. Отрезок единичной длины AB можно разделить на две части точкой С так, что отношение большей части (CB=x) к меньшей (AС=1-x) будет равняться отношению всего отрезка (AB=1) к его большей части (CB): СB/AC=(AC+CB)/CB, т.е. x/(1-x) =1/x. Отсюда имеем выражение:

x² + x - 1 = 0. (1.1)

Положительным корнем этого уравнения является (-1+)/2, так что отношение 1/х в рассматриваемой пропорции равно иррациональному числу:

Ф= 1/х = 1,618033989...

Число 1,618… получило обозначение Ф (PHI) в честь древнегреческого зодчего Фидия (ок. 490-430 до н. э.), который использовал золотую пропорцию в создании скульптур и строительстве храмов. Об этом числе писали Поликлет (5в. до н. э.), Платон (428-348 до н. э.), Евклид (325-265 до н. э.), Витрувий (1в. до н. э.) и др. Величину 1/Ф=0,618…, обратную Ф, обозначают φ. Для реальных вычислений обычно используют Ф=1,618 и φ=0,618. Помимо алгебраического представления, величина Ф может быть вычислена с достаточной точностью по двум процедурам:

по рациональным числам,

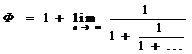
и по иррациональным числам,

Ф=

А.П. Стахов обращает внимание на то, что эти «формулы… вызывают неосознанное чувство ритма и гармонии, когда мы начинаем задумываться над бесконечной повторяемостью одних и тех же простых математических элементов» [160, с. 34].

«Золотая» точка разделяет единичный отрезок в соответствии с золотой пропорцией:

1 : 0,618 = 0,618 : 0,382 = 1,618…

«Долевое» деление единичного отрезка по золотой пропорции имеет вид:

0,382 + 0,618 = 1.

Отметим, что в первом из этих двух выражениий представлена симметрия подобия, где число 1,618 является инвариантом. Во втором выражении представлена асимметрия деления единичного отрезка. Очевидно, что структура представленных выражений не изменится при умножении их элементов на некоторое число А, имеющее любую размерность (см, сек, кал, см³ и т.п.), что имеет большое значение при анализе структуры объектов самой различной «природы».

Следующий важнейший вклад в сокровищницу Математики Гармонии был сделан в 13 веке итальянским ученым Леонардо Пизанским (1170-1240), более известным как Фибоначчи. Фибоначчи был первым крупным математиком средневековой Европы. Ученый изучал труды математиков стран ислама, по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки. В 1202 г. вышло в свет его сочинение «Liber abaci» («Трактат по арифметике»). В книге излагается множество задач. Одна из них ставится и решается следующим образом: «Сколько пар кроликов в один год от одной пары рождается? Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как 1-я пара в 1-м месяце дает потомство, удвой, и в этом месяце окажется две пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце окажется 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родится еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5 и т. д». Свое решение задачи Фибоначчи представляет так: «Мы складываем первое число со вторым, т.е. 1 и 2; и второе с третьим; и третье с четвертым; и так одно за другим, пока не сложим десятое с одиннадцатым, т.е. 144 и 233; и мы получим общее число кроликов, т.е. 377; и так можно делать по порядку до бесконечного числа месяцев». Таким образом, получилась последовательность чисел: 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т. д. Этот ряд чисел в дальнейшем получил название ряда Фибоначчи. Числа ряда Фибоначчи обычно обозначают буквой F. Обозначив число кроликов в n-ый месяц через F_n, а в следующие месяцы - F_n+1, F_n+2 и т.д., последовательность чисел ряда Фибоначчи можно представить обобщенной рекуррентной формулой:

F_n₊₂ = F_n + F_n₊₁.

В дальнейшем И. Кеплер (1571-1630) впервые установил, что F_n+1/F_n ® Ф, а Р. Симпсон (1687-1768) строго доказал, что при достаточном удалении от начала ряда F_n+1/F_n=Ф. Отметим при этом, что при таком удалении в тройке соседних чисел имеет место и симметрия, и асимметрия. Следует добавить, что для любой числовой последовательности с начальными a>0 и b>0 при некотором удалении от начала отношение соседних чисел сходится к величине Ф. Однако наибольшей скоростью сходимости к золотой пропорции обладает последовательность, построенная по числам Фибоначчи [115].

В 19 веке в математике вновь проявляется значительный интерес к золотому сечению. У истоков этого направления стояли два известных французских математика Ф. Люка (1842-1891) и Ж.Ф. Бине (1786-1856). Главным достижением Люка являются его исследования в области «теории чисел Фибоначчи». Он впервые ввел название «числа Фибоначчи». Кроме того, он ввел так называемые «обобщенные числа Фибоначчи», которые формируются по тем же правилам, что и числа Фибоначчи, но при других начальных условиях. Он показал, что среди «обобщенных чисел Фибоначчи», кроме чисел Фибоначчи, особую роль играет еще одна числовая последовательность, названная впоследствии рядом чисел Люка L_n: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76…

Бине является автором знаменитых формул Бине:

F_n=(Фⁿ-(-1)ⁿФ^-ⁿ)/,

L_n=Фⁿ+(-1)ⁿФ^-ⁿ.

В этих формулах целые числа рядов Фибоначчи F_n и Люка L_n получены с использованием иррациональных чисел Ф и . Ряд Фибоначчи F_n: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… A_n-2, A_n-1, A_n,…и ряд Люка L_n: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,… A_n_-2, A_n_-1, A_n,… можно представить обобщенным уравнением:

A_n_-1=A_n_-1+A_n_-2.

Золотое число Ф=1,618… можно представить как фрактальную функцию от рядов Фибоначчи и Люка:

Ф = (L_n₊₁+F_n₊₁)/(L_n+F_n) = (L_n- F_n)/(-L_n₊₁+F_n₊₁),

где n = 1, 2, 3, 4,…..¥.

Отметим, формулы Бине являются как бы связующим звеном между целыми и иррациональными числами. На основании формул Бине украинскими учеными А.П. Стаховым и И.С. Ткаченко [156] были открыты гиперболические функции Фибоначчи и Люка. Основу нового класса гиперболических функций представляет анализ формул Бине и Люка. В отличие от классических гиперболических функций, основанием которых является число е=2,718 (основание натуральных логарифмов), основанием нового класса является число Ф=1,618:

sFs(x) = (Ф^2х-Ф^-2х)/,

cFs(x)= (Ф^2х+Ф^-2х)/.

Эти функции имеют прямое отношение к теоретическому естествознанию. Как показано в исследованиях О.Я. Боднара [20, 21], гиперболические функции Фибоначчи лежат в основе геометрической теории ботанического явления филотаксиса, который известен в науке еще со времен Кеплера.

Нами отмечена [201] полная аналогия между геометрической прогрессией золотых чисел f₁=Ф⁰, f₂=Ф¹, f₃=Ф², f₄=Ф³,..., f_n=Фⁿ^-1, f_n₊₁=Фⁿ, f_n₊₂=Фⁿ⁺¹,…и арифметическим рядом, построенным по рекуррентной формуле f_n₊₂=f_n+f_n₊₁…, где первыми членами ряда являются числа Ф⁰ и Ф¹. «Геометрический» и «арифметический» ряды «золотых» чисел обладают замечательным свойством: числа этих рядов, начиная с первого и дальше, полностью совпадают. Отметим, что подобное совпадение имеет место только для арифметической и геометрической последовательностей с начальными членами Ф⁰=1 и Ф¹=1,618. Аналогично можно представить нисходящую прогрессию Ф⁰, Ф^-1, Ф^-2, Ф^-3,..., Ф^-(ⁿ^-1), Ф^-ⁿ, Ф^-(ⁿ⁺¹⁾ и т. д. и нисходящий арифметический ряд золотых чисел f_n_-2 = f_n - f_n_-1,.., в которых свойство равенства также соблюдается. Естественно, эти отношения сохраняются и при умножении восходящих и нисходящих «золотых» рядов на любую величину A как безразмерную, так и имеющую какую-либо размерность (сек, см, эрг, см³ и т. д.). Любые три соседних числа этих последовательностей заключают в себе симметрию подобия и асимметрию «противоположностей». Отметим, восходящие и нисходящие ряды золотых чисел отражают реальные биофизические и биохимические процессы (см. разделы 2.2 и 2.3).

В 20 веке были получены новые крупные результаты, изменившие сложившиеся представления в современной математике.

Американский математик Дж. Бергман [243] в 12 лет предложил необычный способ позиционного представления чисел:

A=,

где А – действительное число, a_i – двоичная цифра {0,1} i-разряда, i = 0, 1, 2, 3,…, Фⁱ – вес – i-разряда, Ф=1,618 – основание счисления. Основная отличительная особенность «системы Бергмана» состояла в том, что ее основанием является золотое число Ф. С помощью иррационального числа Ф можно представить все действительные числа. Это означает, что любое натуральное число может быть представлено в виде конечного числа степеней Ф. Система Бергмана переворачивает классическое представление о позиционных системах счисления, исторически сложившееся представление о связи рациональных и иррациональных чисел. До открытия Бергмана считалось, что основанием позиционной системы счисления может быть только целое число (10 – для десятичной системы, 2 – для двоичной, 60 – для Вавилонской 60-ричной системы). В «системе Бергмана» основанием системы, т. е. началом исчисления явлется иррациональное число Ф = (1+)/2, с помощью которого можно представить все действительные числа, включая натуральные и иррациональные.

В последней четверти 20 века А.П. Стаховым было сделано важное открытие [153]. Объектом открытия были обобщенные золотые р-пропорции, где классическое золотое сечение является лишь частным случаем. Геометрическая интерпретация рекуррентного соотношения для р-чисел Фибоначчи может быть получена, если мы разделим отрезок АВ точкой С в таком отношении, чтобы AB/CB=x, а CB/AC^p =x^p. Значение искомого отношения АВ/СВ сводится к решению алгебраического уравнения:

x^p+1+ x^p - 1 = 0. (1.2)

Ниже приведены приближенные значения золотых р-пропорций, соответствующие начальным значениям р:

p	0	1	2	3	4	5	6	7	8
Ф_p	2	1,618	1,465	1,380	1,324	1,285	1,255	1,232	1,213

При p=1 уравнение принимает классический «золотой» вид:

x²+ x - 1 = 0.

Корнем данного уравнения является число 1/Ф=(-1+)/2=0,618. По аналогии с классической золотой пропорцией положительный р-корень уравнения называется обобщенной золотой пропорцией или р-пропорцией, а соответствующее деление отрезка - золотым р-сечением.

Значительный интерес к золотым р-сечениям был проявлен в философской науке. Э.М. Сороко возвел их в ранг «закона структурной гармонии систем», который он формулирует следующим образом: «Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоническое строение, стационарный режим существования, структурно-функциональную ...устойчивость» [151]. Эти золотые сечения по отношению к нормированию противоположностей к единице образуют своего рода интерференционную решетку («узлы») - 0,500+0,500; 0,382+0,618; 0,318+0,682;0,276+0,724 и т.д. Их разделяют «пучности» - 0,430+0,570; 0,346+0,654; 0,295+0,705 и т. д. «Узлы» представляют зоны согласованности, устойчивости, а, следовательно, и гармонии самоорганизующихся систем, а «пучности» - зоны неустойчивости и дисгармонии. В качестве обобщения Сороко представил следующий вывод: «Структурная гармония систем природы, т. е. гармония их внутреннего строения, подчиняется четкому математическому закону».

В конце 20 и в начале 21 века аргентинский математик В. Шпинагель [325], французский математик и инженер М. Газале [255], американский математик Д. Каппраф [274] и российский инженер А. Татаренко (167) независимо друг от друга пришли к новому классу математических констант, названных «металлическими пропорциями». Эти пропорции заключены в уравнении

x² -lx-1 = 0, (1.3)

корнями которого являются

Ф_λ=/2,

где λ>0 – любое действительное число. Формула задает бесконечное количество новых математических констант. «Металлические» пропорции или «золотые λ-пропорции» обладают рядом замечательных свойств. Заметим, что при λ=1 «металлическая пропорция» сводится к классической золотой пропорции (1.1). А.П. Стахов пришел к выводу, что «в современной Математике Гармонии успешно развиваются две обобщенные теории золотого сечения: первая основана на «золотых» р-пропорциях, вторая на «металлических» пропорциях» [164]. Классическая золотая пропорция (1.1) является частным случаем пропорций (1.2) и (1.3).

Итак, в основе Математики Гармонии лежит «золотая» парадигма. Ее суть состоит в том что, «начиная какое-либо фундаментальное исследование, мы должны взять за основу «золотую» парадигму, то есть Платоновы тела, золотое сечение, числа Фибоначчи и их обобщения – золотое р-сечение, «металлические» пропорции и вообще всю Математику Гармонии» [205]. Все представленные выше математические соотношения, где отражено «присутствие» числа Ф=1,618, связаны с фундаментальными проблемами современной науки; они представляют Математику Гармонии во многих явлениях окружающего нас мира. По мнению А.П. Стахова, «Интерес к числам Фибоначчи, золотому сечению и проблемам гармонии систем, возникший в современной науке, является подтверждением «естественного» хода развития современной науки, которая приближается к раскрытию законов гармонии, созданию новой научной картины мира, основанной на идеях гармонии, симметрии и золотого сечения (отмечено нами. В.Ц.). Это приведет к восстановлению и углублению связей между Наукой и Искусством как двух взаимно дополняющих методов раскрытия и отображения объективной гармонии Мироздания» [158, с. 212].

1.3. Искусство, наука и золотое сечение

Уже во времена глубокой древности творения человека были связаны с золотым сечением [30]. При археологических раскопках палеолитической стоянки на р. Ангаре (20-25 лет до н.э.) была обнаружена тщательно обработанная прямоугольная пластинка, изготовленная из бивня мамонта; ее размеры с точностью до 1 мм соответствуют прямоугольнику золотого сечения. В пещерах Франции и наскальных изображениях эпохи палеолита и более позднего периода золотая пропорция проявляется в размерах и членениях бизонов, мамонтов и лошадей. В наскальных рисунках возле с. Шишкино на р. Лена, относящихся также к эпохе палеолита, обнаружены изображения диких коней и козла, размеры которых подчиняются пропорции золотого сечения. Известно [151], что многие древнеегипетские архитектурные памятники построены на основе пропорции золотого сечения и чисел Фибоначчи (пирамида Хеопса и др.). С числами Фибоначчи 55, 89, 144 связаны не только внешние пропорции пирамид, но и внутренние - зал фараона (пирамиды Хеопса, Хефрена и Микерина). Золотая или божественная пропорция, являясь чисто математическим соотношением, получила широкое применение в творениях скульпторов и архитектуре Древней Греции. У древних греков все сколько-нибудь крупные архитектурные сооружения (храмы, стадионы, амфитеатры) были построены таким образом, что в них многообразно представлена золотая пропорция. Фригийские гробницы и античный Парфенон, театр в Эпидавре и театр Диониса в Афинах - яркие образцы ваяния и зодчества, исполненные глубокой гармонии на основе золотого сечения. Закон золотого сечения» широко использовался древними греками в архитектурных памятниках (Парфенон), в скульптурах Фидия (5 в. до н. э.), Поликлета (5 в. до н. э.), Мирона (5 в. до н. э.), Праксителя (4 в. до н. э.). «Ничего сверх меры» –этот тезис стал руководящим, центрирующим, собирательным во всех видах творческой деятельности греков. По современному представлению, «…в науке и искусстве Древней Греции «закон золотого сечения» был возведен в ранг главного научного принципа, который охватывал весь Космос и всю науку и искусство в целом» [163]. К этому следует добавить, если в Древнем Египте закон золотого деления использовался «от случая к случаю», то в Древней Греции - постоянно.

В средние века интерес к золотому сечению пропал, свойства этой пропорции были практически забыты. Интерес к «божественному сечению» резко возрос в эпоху Возрождения. Вспомним в связи с этим, что «…эпоха Возрожденья, проложившая широкую дорогу новоевропейской науке, началась с возвращения к забытым проблемам гармонии» [81]. Именно в это время появляется первая книга, полностью посвященная золотому сечению. Книга под названием «Божественная пропорция» (Divine Proportione) была опубликована в 1509 г. известным ученым монахом францисканского ордена Лукой Пачоли ди Борго (1445-1517). В этой книге излагались 12 различных свойств гармонической пропорции. Характеризуя эти свойства, Пачолли пользовался весьма сильными эпитетами: «исключительное», «превосходное», «замечательное», «почти сверхъестественное» и т.д. Раскрывая золотую пропорцию в качестве универсального отношения и в природе, и в искусстве как совершенство красоты, он называл ее «божественной» и склонен был ее рассматривать как «орудие мышления», «эстетический закон», как «принцип мира и природы». Эта книга сопровождалась прекрасными иллюстрациями Леонардо да Винчи, который «закрепил» за золотой пропорцией обозначение «золотое сечение» (sectio aurea). Художник выполнил рисунок, в котором показано, что размах вытянутых в стороны рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и круг. (Интересно, что в этом рисунке Д. Мельхидесеком [106] выявлено золотое соотношение между кругом и квадратом; в эти фигуры вписано тело человека.) Этот рисунок получил название «Витрувийский человек» по имени древнеримского архитектора Витрувия (1 в. до н. э). Л. да Винчи, который безусловно разделял взгляды Пачоли на выдающуюся роль золотого сечения в эстетике и математике. Вслед за Л. Пачоли величайший ученый Средневековья И. Кеплер не менее восторженно говорит о золотом сечении, называя его божественным сечением (sectio divina). Он считал, что «Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении....Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень» [по 272, p. 23]. Он же писал: «Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые Бог ниспослал миру и открыл нам на языке математики» [79]. Имеются свидетельства, что И. Кеплер одним из первых обратил внимание на проявления золотого сечения в ботанике. По мнению Э.М. Сороко, «Теория измерения гармонии по принципу деления в среднем и крайнем отношении…составила тот фундамент, ту стартовую площадку, на которой впоследствии были воздвигнуты и получили движение концепции гармонии в новоевропейской науке и эстетике» [151, с. 76]. Отметим, золотое сечение чрезвычайно широко представлено в произведениях художников и зодчих эпохи Ренессанса. В произведениях Браманте (1444-1514), Л. да Винчи (1452-1519), Рафаэля (1483-1520), Тициана (1477-1576), Микельанджело (1475-1564) и других проявляется строгая размерность и гармоничность сюжета, подчиняющаяся золотому сечению. Знаменитые итальянские мастера Амати (1596-1684), Страдивари (1644-1737) и др. применяли геометрию пентаграммы и золотое сечение в очертаниях своих скрипок. Шедеврами древнерусской архитектуры являются церковь Покрова на Нерли (12 в.), собор Василия Блаженного (16 в.), церковь Вознесения села Коломенское под Москвой (16 в.) и др. [30]. В формах этих сооружений также использованы элементы золотого сечения. После эпохи Ренессанса интерес к золотому сечению на значительное время прервался; в течение более 200 лет эта пропорция была предана забвению. Лишь в 19 веке к золотому сечению и Платоновым телам вновь проявляется определенный интерес, прежде всего в математике. У истоков этого направления стояли два французских математика Ф. Люка и Ж. Бине. Исследования Люка и Бине не были связаны с какими-либо приложениями в теоретическом естествознании. Однако они сыграли большую роль в развитии этого направления в 20 веке.

Интересные исследования об использовании золотой пропорции в шедеврах музыки, живописи и поэзии были проведены в России и СССР Э.К. Розеновым [132], Л. Сабанеевым [138], Г.В. Церетели [204], М.А. Марутаевым [105], Н.А. Васютинским [30]. Выдающийся советский режиссер С.М. Эйзенштейн [221] занимался исследованием золотого сечения в кино. Он сознательно использовал золотое сечение при структурном построении фильма «Броненосец Потемкин», а также при формировании отдельных кульминационных кадров фильма. Большое количество исследований посвящено проявлению золотого сечения в шедеврах древних зодчих и в современной архитектуре [136]. А.Б. Рыбаков показал, что во многих архитектурных шедеврах древности золотое сечение проявляется по антропологическим признакам, т.к. золотая пропорция четко прослеживается в членении тела человека. Интересно отметить, что была установлена связь старинных мер длины (локоть, ступня, различные сажени и т.д.) с золотым сечением [40]. Выдающийся французский архитектор Ле Корбюзье [99] положил золотое сечение в основу своей теории гармонизации в строительстве, известную под названием система «Модулор». В этой системе Ле Корбюзье объединил существующие представления о пропорциях человеческого тела с отношением золотой пропорции.

Во второй половине 19 и первой половине 20 века появились публикации, в которых золотое сечение впервые было установлено во многих закономерностях биологических объектов. Среди них видное место занимают труды немецкого ученого А. Цейзинга [359, 360]. Цейзинг рассматривал золотое сечение как основной морфологический закон в природе и искусстве. Он показал, что этот закон проявляется в пропорциях тела человека, красивых животных и частей растения. Эстетико-математическая система Цейзинга, по мнению А.В. Волошинова [40], «может быть сведена к трем основным положениям: золотое сечение господствует в искусстве; золотое сечение господствует в природе; золотое сечение господствует в искусстве потому, что оно господствует в природе». Г.Т. Фехнером [249] была установлена связь между психофизическим восприятием человека и «золотыми» формами предметов. Т. Кук [44] уделяет большое внимание изучению роли логарифмической спирали в растительных и животных объектах. Им установлено, что феномен роста в биологических объектах связан со спиралями золотого сечения. О значении золотой пропорции в природе и искусстве пишут Г. Тимеринг [168], Г.Д. Грим [52] и М. Гика [44], которые приводят многочисленные примеры проявлений золотого сечения в явлениях природы и различных прикладных искусствах. В 20-х годах прошлого столетия к золотому сечению обращается выдающийся русский ученый и богослов П. Флоренский (1882-1937). В работах Флоренского впервые «золотая» парадигма древних греков рассматривается применительно к естествознанию, а его представления о золотом сечении стали прологом к новым современным открытиям в области квантовой физики, кристаллографии, химии, генетики, которые продемонстрировали фундаментальную роль в современном естествознании. Золотая пропорция становится своего рода «визитной карточкой» красоты и гармонии. В частности, отношение золотого сечения придается форматам книг, бумажникам, шкатулкам и множеству других предметов быта. Закон золотого сечения представлен в музыке, архитектуре, живописи, литературе [30]. Таким образом, золотое сечение – это структурно-математическая характеристика, которая определяет форму прекрасного независимо от того содержания, которое несет в себе форма.

После некоторого ослабления внимания к золотому сечению в первой половине 20 столетия во второй его половине резко возрос интерес к этой пропорции со стороны многих ученых в различных отраслях знаний. Большое влияние на развитие теории чисел Фибоначчи оказали работы советского математика Н.Н. Воробьева [42], впервые опубликованные в 1961 году, и американского математика В. Хоггата в 1969 [265]. Н.Н. Воробьев показал связь золотого сечения с теорией возвратных рядов, комбинаторной математикой, теорией чисел, геометрией, теорией поисков. В. Хоггат установил взаимосвязь между числами Фибоначчи и Люка. В это же время опубликованы замечательные книги А.П. Стахова [153-155]. В этих книгах автором разработаны основы Математики Гармонии - нового направления в математической науке. В СССР публикуется ряд работ, относящихся к разнообразным областям науки: поиску экстремумов унимодальных функций [175], математическом описании принципов оптимизации живых систем [23], организации Солнечной системы [27], лечению некоторых заболеваний человека [57, 145; 166], в экономике [31] и др. В 1963 году математиками Вернером Хоггатом и Братом Альфредом Бруссо была основана Американская Фибоначчи-ассоциация. Это математическая организация, которая специализируется в исследовании последовательности чисел Фибоначчи и широкого спектра смежных вопросов. Начиная с года своего основания, Фибоначчи-ассоциация публикует Международный математический журнал «The Fibonacci Quarterly».

Большой объем исследований по проблеме золотого сечения в СССР и странах СНГ приходится на последнюю четверть 20 и начало 21 века (этот феномен А.П. Стахов обозначил как «славянский взрыв»). В эти годы появились крупные работы в различных отраслях знаний, где золотая пропорция и ее закономерности использованы как своеобразный методологический принцип, лежащий в основе анализа технических и природных систем, их структурной гармонии. Ниже представлены наиболее значительные достижения в этом направлении.

А.П. Стаховым [153, 155] разработана арифметика Фибоначчи, которая была положена в основу компьютеров Фибоначчи. А.П. Стахов и И.С. Ткаченко [156] открыли новый класс гиперболических функций Фибоначчи и Люка. В отличие от классических гиперболических функций, основанных на числе е, гиперболические функции Фибоначчи и Люка основываются на золотом сечении. Главная особенность этих функций состоит в том, что они реально существуют в живой природе, что доказано украинским ученым О.Я. Боднаром [20, 21].

Значительный интерес к золотому сечению и его структурным особенностям был проявлен в философской науке. Белорусский философ Э.М. Сороко [151] выявил фундаментальный характер р-чисел Фибоначчи и золотых р-пропорций, выражающих неизвестные ранее математические свойства треугольника Паскаля. Сороко показал большую роль, которую золотые р-пропорции могут сыграть в процессах самоорганизации систем. Гармоничным (устойчивым, стационарным) состояниям систем объективного мира, по мнению Сороко, соответствуют особые числа, называемые обобщенными золотыми сечениями.

М.А. Марутаев [105] открыл еще одну связь золотого числа Ф=1,618 с симметрией. Это открытие ему удалось сделать благодаря развитой им оригинальной теории качественной симметрии чисел. М.А. Марутаевым на основе качественной симметрии была показана связь числа Ф с числом b=137. Отметим, что число 137 выводится из фундаментальных констант природы - заряда электрона (q), постоянной Планка (ħ) и скорости света (c). Безразмерное число 137 связано с целостностью мироздания, поскольку является отношением фундаментальных констант.

О.Б. Балакшиным [9] получены новые результаты по применению принципов гармонии, симметрии и золотого сечения к проблеме саморазвития динамики подобных систем. Им установлено, что среди немногих по количеству обобщенных вариантов систем особое место занимает золотая пропорция («золотые траектории развития систем»).

Н.Ф. Семенюта [144]) внес значительный вклад в теорию электрических цепей. Благодаря введению понятия лестничных чисел исследователь показал, что числа Фибоначчи являются частным случаем «лестничных» чисел.

С.А. Ясинский [225] провел комплекс исследований в области приложения золотого сечения к электросвязи.

В.В. Очинский [115] исследовал музыкальную гамму с позиций золотого сечения, привнеся принципиально новый взгляд на эту проблему.

А.С. Харитоновым [186] предлагается новая парадигма природы, человека и общества, основанная на золотом сечении.

А.И. Иванус [73] разработал идеи гармоничного менеджемента «по Фибоначчи и золотому сечению».

Н.А. Шило и А.В. Динковым [213]) представлены факты, указывающие на связь Периодической системы Д.И. Менделеева с золотыми числами.

Украинский исследователь С.И. Якушко [224] установил «фибоначчиеву» закономерность в Периодической системе Д.И. Менделеева.

В монографии Яна Гржедзельского «Энерго-геометрический код природы» [262] золотая пропорция рассматривается как пропорция термодинамического равновесия самоорганизующихся систем. Автор показал роль золотой пропорции как универсального кода природы на всех уровнях ее организации.

Открытие квазикристаллов [51] и фуллеренов [60] - выдающиеся достижения современной науки за последние 25 лет - связаны с золотым сечением и числами ряда Фибоначчи:. За открытие фуллеренов, обладающих рядом специфических физических и химических свойств, Р. Керл, Х. Крото и Р. Смолли в 1996 г. были удостоены Нобелевской премии по химии. В 2011 г. Д. Шехтману была присуждена Нобелевская премия по химии за создание квазикристаллов «икосаэдрической» или «пентагональной» симметрии.

Особо следует отметить выдающиеся публикации в первом десятилетии 21 века.

Важнейшим вкладом в Математику Гармонии является публикация на английском языке книги А.П. Стахова «The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science» [333]. Книга представляет не только обзор выдающихся достижений автора в течение 40 лет, но также и вклад других ученых-фибоначчистов в этой области математики.

Известный американский философ Скотт Олсен опубликовал уникальную книгу «The golden section. Nature`s greatest secret» [303]. В книге представлено много оригинальных идей в области золотого сечения и его приложений.

Большой интерес представляет статья на английском языке основателя и президента Международного междисциплинарного общества изучения симметрии (ISIS-symmetry) проф. Денеша Надя [298]. Историческое значение этой статьи состоит в том, что в ней впервые представлена обстоятельная история развития «золотосеченного» направления в России, СССР и постсоветском пространстве, начиная с 19 века и до настоящего времени.

Необходимо перечислить наиболее крупные теоретические и экспериментальные исследования, отнесенные к присутствию золотого сечения в живых системах.

В.Г. Бочков [23] предложил способ нахождения оптимальных состояний любой функциональной физиологической системы по данному измеримому (шкалированному) ее параметру. В частности, он приводит убедительные аргументы тому, что температурный режим млекопитающих, в том числе и человека, явление не случайное, а обусловлено минимумом теплоемкости воды, достигаемым в диапазоне 30 – 40^оС. Этот минимум своей связью с (1/Ф²) объясняет факт устойчивости водной основы земной жизни – структур биоорганизмов.

О.Я. Боднар [20, 21] установил закон преобразования спиральных симметрий, раскрывающий механизм роста и формирования в живой природе. Рост филлотаксисных форм сопровождается изменением симметрии пересекающихся спиралей, количество которых выражается парами чисел - 1/2, 2/3, 3/5, 5/8, 8/13 и т.д. Последовательная смена порядка спиральной симметрии характеризуется гиперболическим поворотом. «Геометрия Боднара» раскрывает механизм роста «филлотаксисных» объектов. В связи с этим заметим, что Г. Вейль рассматривал числовой закон филотаксиса как загадку живой природы. Он утверждал, что «современные ботаники относятся ко всему учению о филотаксисе менее серьезно, чем их предшественники» [32, с. 99].

Российский исследователь С.В. Петухов [118], анализируя связи между длинами в трехчленных блоках тела млекопитающих и человека, а также птиц, установил, что двойное отношение (вурф) в этих блоках приблизительно равно 1,309. Это число, связанное с числом 1,618, является инвариантом по отношению к конформным преобразованиям трехчленных объектов. Петухов [119] предложил оригинальный взгляд на генетический код. Основная идея С.В. Петухова состоит в том, чтобы представить генетические полиплеты в матричном виде. Открытие Петухова показывает глубокую связь генетического кода с золотым сечением. Исследования Петухова показывают фундаментальную роль, которую играет золотое сечение в генетическом кодировании.

А.В. Жирмунский и В.И. Кузьмин [63a] анализируя критические уровни в развитии биологических систем (зачатие, рождение, половая зрелость, смерть), установили, что отношение некоторых важнейших параметров на соседних уровнях характеризуется числом e^е =15,15... C точки зрения преобразований качественной симметрии здесь имеет место золотое сечение [105]. Число e^е является инвариантом преобразований важнейших параметров в процессе развития организма.

В.И. Коробко [89, 90] обнаружил взаимосвязь некоторых интегральных физико-механических характеристик твердого деформируемого тела с золотым сечением. Коробко установлены многочисленные, ранее неизвестные проявления золотой пропорции в деятельности организма человека: его физиологических ритмах, эргономических параметрах «вхождения» в окружающую среду.

М.С. Радюк [126] установил проявления золотой пропорции при изучении скорости осаждения хлоропластов при денатурации гемогената высших растений.

И.Н. Степанов [165] обнаружил многочисленные проявления золотого сечения и чисел Фибоначчи в структуре почвенного покрова, вещественного состава почв и их продуктивности.

И.А. Рыбин [137] в статье «Психофизика: поиск новых подходов» на основании экспериментальных данных показал, что число Ф=1,618 - инвариант психофизических законов, описывающих сенсорные восприятия человека.

П.Ф. Шапоренко и В.А. Лужецкий [209] провели огромное количество измерений скелетов человека и других животных, в том числе и ископаемых, прослеживая эволюционные изменения основных скелетообразующих элементов. Они показали, что гармоническая соразмерность частей тела человека связана с обобщенными золотыми p-пропорциями.

В.Д. Цветков [193, 194] показал, что деятельность сердца в решающей степени связана с золотым сечением и числами Фибоначчи. Вследствие этого сердце работает с минимальными затратами энергии, крови, мышечной и сосудистой массы. Золотые отношения составляют основу законов композиции структур сердечного цикла; эти соотношения справедливы для различных видов млекопитающих.

А.А. Соколов и Я.А. Соколов [147] в статье «Математические закономерности электрических колебаний мозга», показали, что соотношение частот волн (ритмов) электрических колебаний мозга равно золотой пропорции.

А.Г. Волохонский [39] установил соответствие общей структуры генетического кода, ряда биноминального разложения 2 и икосаэдра.

Б.Н. Розин [133] показал, что в результате деления число клеток, возникающих от исходной клетки на каждом шаге деления, подчиняется «фибоначчиевой» закономерности: 1, 2, 3, 5, 8, 13,… .

А.И. Постолаки [122] установил закономерности золотого сечения и чисел Фибоначчи в зубочелюстной системе человека.

В.К. Варин [29] установил соотношение, близкое к золотому сечению в слоистых структурах глаза и слизистой оболочке тонкой кишки.

Таким образом, установлено, что золотое сечение имеет широкое распространение в животном и растительном мире. Представленные выше открытия являются достаточно убедительным подтверждением того факта, что биология приближается к раскрытию одного из сложнейших научных понятий живой природы – понятия гармонии. Можно добавить к этому, в человеке – совершеннейшем творении Природы – пропорция золотого сечения к настоящему времени установлена на самых различных уровнях. Золотое сечение выявлено в работе мозга и сердца, строении глаз и ушей, зубочелюстной системы, параметрах обоняния и вкуса, субклеточных структурах, пропорциях частей лица, рук, ног, других составляющих организма.

1.4. «Простота» Природы, телеология и принцип наименьшего действия

Необходимо предварительно ознакомить читателя с широко используемыми в настоящее время в науке понятиями «простота», «красота», «целесообразность», а также принципами экономии, оптимальности в современном представлении. Эти аспекты наряду с золотыми «противоположностями» имеют непосредственное отношение к анализу деятельности сердца человека и млекопитающих, представленному нами в 2-4 главах.

В начале этого раздела в качестве своеобразного эпиграфа следовало бы привести слова лауреата Нобелевской премии Р. Фейнмана [187]: «Вы не найдете в природе ничего простого, все в ней перепутано и слито. А наша любознательность требует найти во всем этом простоту (отмечено нами. В.Ц.), требует, чтобы мы ставили вопросы, пытались ухватить суть вещей и понять их многоликость как возможный итог действия сравнительно небольшого количества, на все лады сочетающихся между собою». Эта мысль высказана выдающимся физиком полвека назад. Однако и в наши дни «простота» природы по-прежнему находится в центре внимания естественных наук. Стремление к простоте, ясности и универсальности всегда лежало в основе теоретического естествознания. С точки зрения диалектики сложность неотделима от простоты. Как считает российский философ Н.Ф. Овчинников [114, с. 328], «сложность природы не может быть понята в самой себе без того, чтобы человеческая мысль не нашла скрытую за ней простоту самой природы».

Математическая «простота» все чаще становится синонимом «красоты». В.М. Волькенштейн сформулировал признаки «красоты» в науке: 1) эстетическое впечатление возникает только в связи целесообразным, трудным преодолением; 2) красиво сведение сложного к простоте (отмечено нами. В.Ц.); 3) всякое математическое оформление научных достижений, если оно наглядно и гармонично, вызывает эстетическое наслаждение» [по 40, с. 35]. Академик Л.А. Арцимович предложил универсальное правило при оценке решения проблемы: «Самое правильное – самое простое». Сложность систем может быть представлена внешне весьма простыми математическими отношениями. Тем не менее, простая с виду математическая формула иногда вмещает в себя десятки страниц научного текста.

Вспомним, философские постулаты пифагоризма заключались в признании гармоничности, простоты и красоты всего сущего, начиная с Космоса и заканчивая микромиром. В подтверждение последнего признака можно было бы привести высказывания многих великих ученых (Платон, Н. Коперник, Г. Галилей, У. Гамильтон, В. Гейзенберг, М. Планк, А. Эйнштейн и др.). Среди многих выдающихся ученых нашего времени начинает преобладать представление о том, что красивые и гармоничные формулы и уравнения вызывают большее доверие к их достоверности, чем математические выражения, не обладающие этими достоинствами. В наши дни «простота» все чаще отождествляется с «красотой» представляемой теории (красиво сведение сложного к простоте). Академик А.Б. Мигдал (1911-1991) писал по этому поводу: «В физике последнего времени на первый план переместилось понятие красоты теории. Красота теории имеет в физике почти определяющее значение» [107]. Лауреат Нобелевской премии П. Дирак (1902-1984) также был убежден в том, что «физические законы должны обладать красотой» [56, с. 5]. Отметим, одной из главных задач нашей книги является показать математическую «красоту» и «простоту» структуры и организации сердца человека и млекопитающих.

Прежде чем обратиться к выявлению математической основы гармонии живых систем, следует рассмотреть некоторую аналогию между математикой, «простотой» и «красотой» природы. Многие столетия ученые самых различных областей знаний стремились представить установленные закономерности простыми формулами или простыми числовыми отношениями. На основе этих традиций и возник один из основных критериев истины – «простота», родились крылатые выражения: «Все гениальное – просто», «Природа стремится к простоте». Еще в 14 веке францисканский монах и философ У. Оккама (1285-1349) был убежден в том, что «чем ближе мы находимся к некоторой истине, тем проще оказываются законы, выражающие эту истину» [по 50, с. 140]. Ему же принадлежит утверждение: «То, что можно объяснить посредством меньшего, напрасно выражать посредством большего». В трактовке А. Эйнштейна это означает: «Все должно быть сделано настолько просто, насколько возможно, но не проще этого». Мысль о том, что «природа действует простейшим образом», т.е. наиболее экономно, принадлежит И. Бернулли (1667-1748). Это утверждение послужило источником многих научных идей и методических приемов. Отметим, однако, тезис «природа любит простоту» и в наши дни все еще оспаривается и подвергается сомнению среди части ученого сообщества. Но еще в начале 20 века великий французский математик А. Пуанкаре (1854-1912) писал по этому поводу: «…даже те, кто не верит более в простоту природы, принуждены поступать таким образом, как если бы они разделяли эту веру; обойти эту необходимость значило бы сделать невозможным всякое обобщение, а, следовательно, и всякую науку» [по 174, с. 275]. Ведь если не руководствоваться критерием простоты, то невозможно выбрать какое-либо теоретическое обобщение из множества различных вполне осуществимых обобщений. Иначе говоря, Пуанкаре утверждал, что во всех случаях надо исходить из гипотезы простоты природы. Поиск «простоты» в своей основе предполагает целенаправленный (телеологический) подход к изучаемому объекту. Таким образом, конечная цель научного исследования состоит в выявлении «простоты» там, где еще недавно царил хаос. Этот принцип построения физических теорий впоследствии стали называть «принципом простоты». Полученные при этом математические выражения отображают «простоту» и «красоту» Природы.

Современный анализ практически невозможен без использования математики, поскольку математика - наиболее эффективное средство для решения возникающих проблем. Не подлежит сомнению, что критерий истинной науки состоит в его отношении к математике. Выдающийся математик 20 века Г. Вейль писал по этому поводу: «В природе существует внутренне присущая ей скрытая гармония, отражающаяся в наших умах в виде простых (отмечено нами. В.Ц.) математических законов. Именно этим объясняется, почему природные явления удается предсказывать с помощью комбинации наблюдений и математического анализа. Сверх всяких ожиданий убеждение (я бы лучше сказал – мечта!) о существовании гармонии в природе находит все новые и новые подтверждения в истории физики»» [по 79, с. 399]. Вейль был уверен, что математика отражает порядок, существующий в природе. Ни один закон природы ученый не может «выдумать» – он лишь находит его в окружающем его мире. То же самое и в математике: математический закон ученый может найти лишь в природе. По мнению выдающегося физика Ю. Вигнера (1902-1995), «утверждение о том, что природа выражает свои законы на языке математики... в наши дни ...верно более чем когда–либо» [33, с. 192]. Важнейшая особенность математики состоит в том, что с древнейших времен и до наших дней развитие ее понятий и методов исходит из опыта. М. Клайн по этому поводу пишет: «Математические понятия и аксиомы берут свое начало из наблюдений реального мира (отмечено нами. В.Ц.)» [79, с. 378]. За много веков человек создал такие великие построения, как евклидова геометрия, птоломеева система мира, механика Ньютона, теория электромагнитного поля, теория относительности, квантовая теория. Математика является неотъемлемой частью всех этих и многих других теорий, их основой и сущностью, инструментом науки, который сложное и многообразное делает простым и единообразным. Важнейшая роль математики заключается в том, что она «…выполняет миссию посредника между человеком и природой» [79, с. 383]. Об эффективности математики в естественных науках при описании природы высказывались многие выдающиеся физики и математики: А. Пуанкаре, А. Эйнштейн, Г.Вейль, В. Гейзенберг, П. Дирак, Э. Шредингер и многие другие.

Возникает вопрос, что же могло обусловить столь тесную связь реальных физических объектов с формулами и теориями абстрактной математики? По-видимому, те принципы, которые были заложены в качестве исходных при возникновении и развитии математики. Начало возникновения математики скрыто в глубине тысячелетий. Казалось бы, невозможно установить те исходные принципы, которые составили общую исходную методическую основу математики. Определенные истоки понимания этого содержатся в книге М. Клайна [79, с. 48]: «…у греков, начиная с 6 в. до н. э., сложилось определенное миропонимание, сущность которого сводится к следующему. Природа устроена рационально, а все явления протекают по точному и неизменному плану, который, в конечном счете, является математическим». Из этой цитаты видно, что древними математиками в качестве исходной была принята телеологическая гипотеза о рациональном, целесообразном устройстве мира. Тем самым, они как бы заложили тысячелетний опыт по проверке результативности телеологического принципа (принципа о целесообразном устройстве мира) в развитии науки. Утверждая телеологичность математики, П. Дирак отмечал глубинную связь математики и физики: «Математик играет в игру, правила которой он изобрел сам, а физик – где их изобретает Природа, но постепенно становится все более очевидным, что правила, которые математика считает интересными, совпадают с теми, что задает природа» [56]. В основе такого подхода к объекту лежит предположение, что цель есть «разумный акт», осуществляемый в Природе ее объективными силами. Учение о целях получило обозначение «Телеология». В той мере, в какой цель есть несомненно существующий факт, телеология несомненно имеет научное значение, представляя собой объяснение этого факта. Наш современник академик Н.Н. Моисеев писал по этому поводу: «…Общей закономерностью у сознательного целеполагания и несознательного функционирования самоуправляемой системы любой природы является направленность к достижению определенного результата» [108, с. 80]. Согласно телеологическому подходу любая живая система в течение своей эволюции имеет свою цель (совершенство). Многие современные биологи до сих пор несколько пренебрежительно относятся к телеологии. Тем не менее, широко известно шутливое утверждение: «Телеология - дама, без которой не может прожить ни один биолог, но с которой он, однако, стыдится появляться в обществе».

В настоящее время основу целенаправленного подхода к объекту составляют экстремальные принципы. Следует вспомнить при этом, что аспекты экстремальности привлекали внимание математиков с древних времен. Например, пифагорейцы обращали особое внимание на уникальные геометрические объекты – круг (окружность) и шар (сфера). Круг является единственной фигурой, у которой максимум площади имеет место при минимальном периметре; шар имеет максимум объема при минимальной поверхности. Идея экстремальности свойств геометрических объектов в дальнейшем нашла свое отражение в поисках и выявлении общих принципов экстремальности в механике и различных разделах физики. По мнению И.А. Ассеева [5, с. 215], «наука только тогда достигает теоретического уровня развития, когда начинает активно использовать экстремальные (отмечено нами. В.Ц.) принципы для формулировки своих основных теоретических положений и на этой основе широко применять экстремальные математические методы». Справедливость этого утверждения подтверждается историей механики и физики – наук, достигших наиболее высокого развития, а также успехами в построении теоретической кибернетики и биологии. Проблема выявления экстремальных принципов и законов расхода энергии движущимися объектами уходит своими корнями в далекое прошлое. Впервые эффект экстремальности был установлен французским математиком Ферма (1601-1665). Было установлено, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех других путей, соединяющих эти точки. Из всех возможных луч «выбирает» такую траекторию, при которой время движения минимально. Этот феномен в дальнейшем получил название - принцип Ферма. Принцип Ферма является исходным принципом геометрической оптики. Как отмечено Д.В. Сивухиным [145, с. 47], при обосновании этого принципа «Ферма руководствовался телеологическими соображениями, согласно которым природа действует целенаправленно, она не может быть расточительной и должна достигать своих целей с наименьшими (отмечено нами. В.Ц.) затратами средств». Ученые 18 века были убеждены в том, совершенная Вселенная не терпит напрасных затрат и поэтому каждое действие природы должно быть наименьшим из всех возможных. В 1740 г. французский ученый П. Мопертьюи (1698-1759) при анализе траекторий движения планет установил принцип наименьшего действия (ПНД). Этот принцип был сформулирован следующим образом: «Количество действия, необходимое для того, чтобы произвести некоторое изменение в природе, является наименьшим возможным» [110, с. 5]. (Величина «действия» выражается произведением энергии на время). Величайший математик 18 века Л. Эйлер (1707-1783) в 1744 г. преобразовал принцип наименьшего действия в принцип экстремального действия, который имеет два принципиально различающихся решения: минимальное и максимальное. Дальнейшее прогрессивное развитие экстремального принципа в физике в приложении не к отдельным точкам, а к системам принадлежит Ж. Лагранжу (1736-1813). Принцип наименьшего действия по существу стал центральным принципом вариационного исчисления – новой области математического анализа, основателем которого стал Лагранж, опирающийся на труды Эйлера. Из обобщенного принципа наименьшего действия удалось получить решение многих задач механики. Впоследствии было показано, что разработки Лагранжа имеют отношение только к классической механике и не пригодны для использования в других разделах физики. Последующие усовершенствования понимания принципа наименьшего действия и математического его выражения были выполнены ирландским ученым У.Р. Гамильтоном (1805-1865). Гамильтон одним из первых обнаружил близость по своей сущности принципа наименьшего действия принципу Ферма. На основе представлений о единстве мира, о красоте и гармонии природы он связывал этот принцип с общим методом Лагранжа в теоретической физике, подчеркивая особую важность этого метода. Формулировку принципа наименьшего действия Гамильтон дает в вариационной форме, исходя из представлений об экстремумах, подобно своим предшественникам – Эйлеру и Лагранжу. Наиболее точно и понятно принцип наименьшего действия, отображенный в уравнениях Гамильтона, выразил А. Пуанкаре [125, с. 103]: «Все перемены, какие могут происходить с телами природы, управляются двумя экспериментальными законами: 1) сумма кинетической и потенциальной энергии не меняются. Это принцип сохранения энергии; 2) если система тел в момент t₀ имеет конфигурацию А, а в момент t₁ конфигурацию В, то переход от первой конфигурации ко второй всегда совершается таким путем, что среднее значение разности между двумя видами энергии за промежуток времени от…до является величиной самой малой из всех возможных».

Следует отметить, что в математическом отношении уравнения Лагранжа и Гамильтона представляются тождественными, но по физической сущности они принципиально различаются. Уравнение Гамильтона, отобразившее наиболее полно принцип наименьшего действия, обеспечило возможность успешного использования его не только в классической механике, но и в других разделах физики. Экстремальные принципы поражают не только своей общностью, но и фундаментальной ролью в построении различных разделов теоретического естествознания и, особенно, теоретической физики. В наши дни особая важность принципа наименьшего действия для теоретической физики уже не вызывает сомнений. Исходными положениями основных разделов физики являются экстремальные принципы, которые надежно установлены на основе эмпирических обобщений и математического анализа. Лауреат Нобелевской премии М. Борн (1882-1970) отмечал, что «свойства минимальности мы встречаем во всех разделах физики и они являются не только верными, но и крайне целесообразными…для формулировки физических законов» [22, с. 113]. Ниже представлено основополагающее «присутствие» принципа наименьшего действия в основных разделах современной физики.

Возникновение специальной и общей теории относительности явилось важнейшим этапом развития теоретической физики. Теория относительности выявила ограниченность основных исходных положений классической механики. Исключение составил принцип наименьшего действия в форме Гамильтона. В основном уравнении геометродинамики – уравнение Эйнштейна – Гамильтона – Якоби [178] - в неявном виде отображен принцип наименьшего действия. В общей теории относительности 4-мерная симметрия пространства-времени остается в силе. Эта симметрия, выполняющая очень важную роль в теории относительности, находится в согласии с принципом наименьшего действия. В связи с этим величина действия является наиболее универсальной величиной, характеризующей одновременное изменение системы в пространстве-времени.

Уравнения Гамильтона имеют отношение и к другим разделам физики. «Основные уравнения квантовой электродинамики – уравнения Дирака и Паули содержат гамильтониан» [14, с. 150]. Аналитически величину неопределенности законом неопределенности Гейзенберга также удалось выразить на основе уравнения Гамильтона. В основные уравнения квантовой механики – уравнения Шредингера – гамильтониан входит в виде оператора [96]. В качестве основы исходного уравнения Шредингера использована волновая функция классической оптики (выводимая из принципа Ферма), в которую введен в качестве оператора гамильтониан. Рассматривая развитие физических представлений в квантовой механике, П. Дирак отмечает: «Интересно, однако, что квантовое состояние не просто соответствует классическому состоянию. Оно соответствует целому набору классических состояний, связанных друг с другом особым математическим способом…Каждое квантовое состояние отвечает одному из гамильтоновых семейств классических состояний» [56, с. 72]. Заметим, что квант действия – постоянная Планка - имеет ту же размерность, что и величина «действие» по принципу наименьшего действия.

Макроэлектродинамическая теория Максвелла не содержит в явном виде подобных принципов, но она также по существу феноменальна. Связь макроэлектродинамических уравнений Максвелла и Гамильтона показана Д. Тер Хааром [182]. Все основные аналитические зависимости и законы геометрической оптики выводятся из принципа Ферма, согласно которому луч света, распространяясь из одной точки в другую, проходит траекторию, соответствующую наименьшему времени прохождения. Принцип Ферма по своей сущности тождественен принципу наименьшего действия [97]. Закон электромагнитной инерции Ленца также можно рассматривать как принцип минимизации перехода магнитной энергии в электрическую энергию и наоборот. В этом отношении он явно тождественен принципу наименьшего действия, которым определяется минимизация перехода в механических процессах потенциальной энергии в кинетическую и наоборот [141].

Принцип наименьшего действия широко используется в современной физике и системном анализе. Всеобщность и универсальность принципа наименьшего действия для физики заключается в том, что он является вариационным принципом. Сложность объяснения «присутствия» экстремальных принципов в природе состоит в том, что их невозможно вывести из более общих принципов и законов, так как в общей формулировке они сами являются предельно общими. Все попытки вывести экстремальные принципы из физических законов и принципов оказались несостоятельными. Отметим, принцип наименьшего действия дает полную физическую характеристику движения системы, в то время как закон сохранения и превращения энергии рассматривает протекание явлений во времени. С математической точки зрения неодинаковое значение обоих принципов состоит в том, что принцип сохранения, применяемый к конкретному случаю, дает только одно уравнение. Тогда как для полного изучения необходимо столько уравнений, сколько имеется независимых координат. Принцип наименьшего действия в каждом конкретном случае дает как раз столько уравнений, сколько имеется независимых координат.

Наконец, мы можем обратить внимание читателя на «присутствие» принципа экстремальности в биологии. По мнению М. Планка (1858-1947), «принцип наименьшего действия в понятие причинности вводит совершенно новую мысль: к causa efficients – причине, которая действует из настоящего в будущее и представляет более поздние обстоятельства как обусловленные прежними, добавляет causa finalis, которая, напротив, делает предпосылкой будущее, а именно определенно направленную цель, а отсюда выводит течение процессов, ведущих к этой цели». «Развитие физики, отмечает далее Планк, привело к формулировкам, имеющим выраженный телеологический (отмечено нами. В. Ц.) характер. Но это не внесло ничего нового или противоположного в закономерности природы. Просто речь идет о другой по форме, а по сути дела совершенно равноправной точке зрения» [305, S. 25]. Планк пришел к обобщающему выводу о том, что «…высшим физическим законом, венцом всей системы является …принцип наименьшего действия» [120, с. 68]. Можно сказать, что все энергетические принципы, составляющие основу физики, по своей сущности являются природными механизмами энергоэкономности. И. Пригожин [123] показал, что для объяснения физических основ жизни не требуется создания новой физики с введением новых констант, как это потребовалось при создании механики микромира. Пригожин отмечал, что «классическая или квантовая физика описывает мир как обратимый и статичный» [124, с. 8]. Поскольку биология объясняет эволюцию мира живой природы, нельзя говорить об обратимости эволюционных процессов в организме. По мнению известного биофизика А.А. Блюменфельда (1921-2002), «проблемы, возникающие при рассмотрении упорядоченности биологических структур, ее создания и эволюции, не лежат в области физики», поскольку «физика не претендует на объяснение природы...(она) пытается объяснить лишь закономерности в поведении различных объектов» [16, с. 45]. Биология сводима к физике лишь в том смысле, что физические законы раскрывают основу энергетики биологических процессов. Добавим, что перенесение из физики в биологию экстремальных (оптимальных) принципов, связанных с энергией, позволило использовать в этой науке экстремальные математические методы. Заложенные в них идеи «простоты», оптимальности и экономии энергии как нельзя лучше соответствуют давнему представлению о совершенстве и целесообразности живой природы. В 2, 3 и 4 главах нами будут представлены внешне «простые» математические формулы, которые отражают гармонию «противоположностей», энергооптимальность и экономию строительного вещества в сердечных системах сердца человека и млекопитающих.

1.5. Биологические системы, самоорганизация и энергооптимальность

По все еще широко распространенным в наши дни представлениям строение каждого органа целиком определяется как эволюционное приспособление к условиям окружающей среды и непосредственным функциональным нагрузкам этого органа. Известно, однако, что при всем фантастическом разнообразии объектов и процессов в живой природе те или иные формы организации очень часто повторяются. Известный биолог-теоретик А.А. Любищев обращал внимание на то, что «несмотря на гетерогенность и исключительную сложность в строении организмов… имеется проникающая всю систематику повторяемость сходных форм, наводящая на мысль, что формы организмов не являются эпифеноменами сложной структуры» [по 1, с. 51]. Одинаковые формы нередко могут быть представлены у множества объектов, даже не имеющих генетического родства. Феномен сходства имеет широкое распространение в живой природе (например, форма листьев, венчиков цветков растений и молекул). Отнюдь не случайно также сходство формы объектов живой и неживой природы (морозные узоры на стекле и рисунок растений, спирали галактик и раковин и т.д.). В самостоятельной роли формы можно убедиться хотя бы по тому, что живые системы чаще всего имеют форму сферы, цилиндра, спирали, дерева [62, 1979]. Все эти конструкции обладают уникальными свойствами. Спираль позволяет уместить огромный запас информации в малом пространстве и в то же время отрезок спирали является кратчайшим расстоянием между двумя точками на поверхности цилиндра. По спирали закручиваются усики растений, происходит рост тканей в стволах растений, спиральные движения наблюдаются при росте корней и побегов. Листья на побегах растений, возникающие и располагающиеся по винтовым спиралям в наименьшей степени затеняют друг друга. В корзинках сложноцветных при формировании соцветий по спиралям образуется их наиболее плотная упаковка. Использование спиральных элементов придает живым конструкциям максимальную жесткость при минимальном расходе энергии [46]. По спирали осуществляется движение протоплазмы в клетке и рост самой клетки. Развитие зародыша у человека и млекопитающих также происходит со спиралеобразной закруткой вдоль главной оси [118]. Цилиндр имеет максимальную жесткость по отношению к другим полым вытянутым фигурам (например, полый параллелепипед или призма). Форма шара обеспечивает минимальный расход материала на оболочку при максимальной жесткости сферической оболочки. «Дерево» позволяет эффективно снабжать ткани кровью и кислородом с минимальной затратой сосудистого материала и крови; эта форма представлена в сердечных системах и, так или иначе, связана, как будет показано нами в 2-3 главах, с золотым сечением и числами Фибоначчи. Примеры, как самоорганизующаяся природа бережно сохраняет и использует ценную информацию на протяжении всех этапов ее эволюции, наглядно продемонстрированы Лима-де-Фариа [100] в книге, посвященной эволюции природы и, в частности, биологической эволюции. В ней на многочисленных иллюстративных примерах аналогий между структурами физико-химических и биологических объектов показано, что ценная информация, созданная природой на физико-химическом этапе эволюции и осуществленная в соответствующих энергоэффективных (энергоэкономных) структурах, используется и на биологическом этапе эволюции.

Несомненно, что каждой живой системе присуща целесообразность, аспект «оправдывающий» создание и эволюцию данной системы. Еще Аристотель считал целесообразность (функцию) биологических систем краеугольным камнем в понимании биологических явлений, «ибо не случайность, но целесообразность (отмечено нами. В.Ц.) присутствует во всех произведениях природы и притом в наивысшей степени» [4, с. 50]. Не вызывает сомнения, что целесообразность (функция) является универсальным атрибутом всех организмов и живых систем. Следует выяснить, какие универсальные критерии лежат в основе функционирования биологических объектов? Какой механизм самоорганизации является главным, определяющим деятельность всего организма? Ответом на эти вопросы является энергооптимальная самоорганизация живых систем. Этот феномен следует из второго постулата принципа оптимальности, открытого создателем неравновесной термодинамики И.Р. Пригожиным [123]. Этот принцип сформулирован в форме вариационного принципа минимума диссипации (рассеяния) энергии: если возможно множество сценариев протекания процесса, согласных с законами сохранения и связями, наложенными на систему, то в реальности процесс протекает по сценарию, которому отвечает минимальное рассеяние энергии. В применении к живым системам этот критерий определяет устойчивость стационарного состояния, в котором скорость производства энтропии, и, следовательно, рассеяния энергии минимальна. Биолог-теоретик И.И. Свентицкий [142] обосновал энергетическую экстремальность самоорганизации и прогрессивной эволюции природы в соответствии с целеполагающим принципом, что еще раз подтверждает разумность применения телеологического принципа в развитии научных знаний. В соответствии с выдвинутым И.И. Свентицким законом выживания каждый элемент самоорганизующейся природы в своем развитии самопроизвольно устремлен к состоянию наиболее полного использования доступной свободной энергии в существующих условиях [142]. В законе выживания представлен энергетический приоритет оптимального развития самоорганизующихся живых систем. Энергетическая часть занимает в организме «привилегированное» положение. Отметим, что основная часть информационных или управляющих процессов направлена на обеспечение функционирования подсистемы энергообмена, на сохранение ее структур. «…С операционной точки зрения кибернетические механизмы для того и существуют, чтобы обеспечить стабилизацию и сохранение энергетической (отмечено нами. В. Ц.) части организма» [179, с. 8]. Об этом же пишет А.П. Руденко [134, с. 11]: «Подсистемы обмена веществ и информационных или управляющих процессов функционально и структурно подчинены подсистеме энергообмена. Факторы прогрессивной эволюции также имеют энергетическую природу». Проявление этих процессов, подтверждающих этот закон на микроуровне, доказано в работах М. Эйгена [219], Г. Хакена [184] и А.П. Руденко [135]. Таким образом, Эффективность функции в своей основе обусловлена энергетическим аспектом. Для биосистем установлено [143], что самоорганизация этих систем означает приведение их к «наилучшему», энергооптимальному виду.

Как отмечалось нами раньше, всякий системный параметр существует в пределах диапазона возможных значений, при которых нормальная деятельность системы еще сохраняется. Внутри этого диапазона по отношению к некоторой «рабочей» величине всегда существуют участок допустимых положительных приращений и участок допустимых отрицательных приращений параметра. «Рабочее» значение параметра по разным причинам может изменяться; при этом меняется также и числовое соотношение между «положительным» и «отрицательным» участками. При этом поиск нового энергетического оптимума происходит по четко очерченной схеме [175]; минимизация расхода энергии системой происходит за некоторое ограниченное количество операций или тактов по числам Фибоначчи. На этот же феномен указывает Э.М. Сороко [151, с. 90]: природа «реализует поиск оптимума структурных состояний не «вслепую», «методом проб и ошибок», …, а более сложно – «по стратегии Фибоначчи». Таким образом, механизм поиска оптимального режима связан с особенностями ряда чисел Фибоначчи! Добавим к этому, что на реализацию энергетических потребностей организма животных используется «золотая» доля его массы (38%) [26]. Этот «золотой» показатель сохраняется для различных представителей животного мира, включая и человека.

Во второй половине 20 века экстремальные закономерности привлекли внимание многих биологов. В биологии стали формулироваться вариационные принципы и использоваться математические методы. Применение математических экстремальных методов в биологии связывается рядом авторов с принципом оптимальной конструкции организма [128, 131, 241, 242]. Н. Рашевский впервые выдвинул гипотезу об энергооптимальности организма: «Организм имеет оптимально возможную конструкцию по отношению к экономии используемого материала и расходования энергии, необходимых для выполнения заданных функций» [308]. Такой подход оказался одним из наиболее плодотворных. Согласно формулировке Н. Рашевского конструкция организма в отношении энергии и используемого строительного материала оптимальна. Н. Рашевский [128] и Р. Розен [131] применили принцип оптимальной конструкции при рассмотрении зависимости размеров сердца, легких, кровеносной системы млекопитающих, особенностей работы этих органов от выполнения главной биологической задачи, которой они подчинены. Проведенные расчеты показали хорошее совпадение с экспериментальными данными. Таким образом, принцип оптимальной конструкции в формулировке Рашевского можно считать не чем иным, как обобщенным «представлением» принципа максимальной экономии энергии и вещества по отношению к выполняемой функции. К работам, в которых рассматривается энергооптимальное функционирование живых систем, следует также отнести исследования М.А. Ханина [185, 279]. В этих работах состояние системы транспорта кислорода, включающей сердечно-сосудистую систему, систему внешнего дыхания и кроветворения, определяется на основе критерия, формулируемого как требование минимума суммарной энергии, потребляемой этими системами. Теоретические величины функциональных параметров, определяемых на основе экстремальных принципов, так же как и структурные параметры, оказались в хорошем соответствии с данными, полученными в результате биофизических исследований. Следует отметить, что энергетическая оптимизация установлена на многих других биообъектах [23, 113,141, 142, 185]. Большинство авторов, используя принцип экономии энергии, ограничиваются количественными предсказаниями и выводом отдельных констант и закономерностей. На этом фоне значительный интерес представляет работа Л.Б. Емельянова-Ярославского [61]. Автор исходит из предположения, что нейрон в своей деятельности решает единственную задачу – экономию энергии. Все остальные функции мозга – память, восприятие внешней среды, сон, сознание, подсознание, эмоции, интелект – возникают как побочные продукты этой деятельности. Примеры экономии энергии и строительного материала в растительном мире можно найти в интересной книге Ю.С. Лебедева [98].

Конечно, к проблеме критерия оптимальной работы организма можно подходить не только со стороны энергетики. Например, для анализа его гемососудистой системы, обеспечивающей доставку кислорода к тканям, может быть использован один (или несколько) из следующих критериев: минимальный расход энергии в сосудах, минимальное сопротивление движению крови, минимальный объем крови и сосудистого вещества, минимальное напряжение сдвига на стенках сосудов и т.д. Вопрос состоит в том, какой из этих критериев Природа «предпочитает» остальным? В дальнейшем нами в 3 и 4 главах будет рассмотрена оптимальность многих энерго-вещественных параметров гемососудистого русла сердца. Сейчас же отметим, что оптимизация сосудистого русла с позиции различных критериев исследуется с давних пор. Оптимизации сосудистых бифуркаций (разветвлений) был посвящен целый ряд математических исследований [243, 244, 274, 295; 340, 357, 358 и др.]. При этом использовались различные критерии оптимальности: минимум мощности [295], минимум объема [274], минимум площади поверхности сосудов [357] и др. Теоретический анализ энергетической оптимальности конструкций кровеносного русла был произведен в работах [11, 72, 216 и др.]. В конечном счете, было установлено [357], что в области параметров гемодинамики, имеющих физиологическое значение, оптимальные результаты, полученные с помощью перечисленных критериев, весьма близки друг к другу. В связи с доминированием в организме системы энергообеспечения, можно считать, что в физиологических пределах основным, ведущим является энергооптимальный критерий, которому «сопутствуют» и остальные перечисленные критерии оптимизации системы кровоснабжения. Необходимо отметить, сопряжение нескольких критериев оптимальности установлено нами в гемососудистой системе сердца [191-194]. Было показано, что основу функционирования этой системы составляет сопряжение оптимальных критериев минимизации затрат энергии, крови и сосудистого материала.

1.6. Системный подход, принцип оптимального вхождения и гармония

Выдающийся русский ученый К.А. Тимирязев в начале прошлого века обращал внимание на то, что «для полного познания сущности объекта недостаточно ответить на вопрос, как он устроен, необходимо также знать, почему он устроен именно так?» Эта проблема по-прежнему актуальна и в наше время. Сложность решения этой задачи заключается в том, что вплоть до наших дней стратегию научного поиска составляет преимущественно редукционизм - расчленение целого на все более «простые» части. Необходимо отметить, что на этом пути были получены выдающиеся практические результаты. По этой причине синтез как метод, обратный редукционизму, временно потерял свою привлекательность. Однако редукционистский метод в своей основе имеет принципиальный недостаток: объект исследования исчезает как целое, как система со всеми ее особенностями. На это обстоятельство обращал внимание И. Пригожин [124, с. 11]: «…цивилизация достигла необычайных высот в искусстве расчленения целого на части, а именно в разложении на мельчайшие компоненты. Мы изрядно преуспели в этом искусстве, преуспели настолько, что нередко забываем собрать разъятые части в то единое целое, которое они некогда составляли (отмечено нами. В.Ц.)». При дроблении объекта на все более мелкие части неизбежно утрачивается часть информации о связях и взаимодействии между частями и целым. Естественно, при таком подходе невозможно установить организацию и гармонию целого объекта («почему он устроен именно так?»). Попытки понять мир, только исходя из принципов редукционизма, изначально несостоятельны, поскольку целое не сводимо к сумме своих частей. Целое определяет поведение частей, а не наоборот. Вспомним античный афоризм: «Целое больше частей». Не увидев целого, невозможно понять внутренней простоты и логичности Природы. Устранение этого недостатка становится возможным благодаря тому, что в современной науке возникает синтезирующий, системный, идеал научного мышления и обобщения. Системный метод ориентирует исследователя на раскрытие целостности объекта, на выявление многообразных типов связей в нем и сведение их в единую теоретическую картину.

Выдающийся советский математик и кибернетик А.А. Ляпунов (1911-1973) считал, что «системные исследования имеют важную координирующую и направляющую роль для гармонического развития многих областей биологии» [104]. Создание общей теории систем (ОТС) явилось итогом усилий нескольких поколений выдающихся деятелей науки. Основы единого научного подхода к изучению живых систем были заложены в начале 20 века русским ученым А.А. Богдановым [19]. Однако начало общего интереса к проблемам теории систем принято относить к публикации в 40-х годах прошлого столетия первых работ австрийского биолога Л. фон Берталанфи [15], во многом повторяющих те же общие представления, которые сформулировал А.А. Богданов. В настоящее время общая теория систем является уже достаточно развитой теорией. Для нас наибольший теоретический и практический интерес представляет вариант ОТС(У) Ю.А. Урманцева [180], разработавшего начала ОТС - фундамент системологии. Урманцев показал глубокое единство органического и неорганического мира, вытекающее из системной природы любых объектов. В настоящее время по признанию многих исследователей и практиков ОТС(У) является наиболее продвинутым и самым используемым вариантом ОТС. Разработанный Урманцевым вариант ОТС включает в себя понятия «объект», «объект-система» и «закон композиции». За «объект» признается любой предмет мысли, т. е. предметы объективной и субъективной реальности, и не только вещи, но также качества, свойства, отношения, процессы, параметры и т.д. «Объект-система» - это единство, созданное определенного сорта «первичными» элементами + связывающими их в целое отношениями (в частном случае, взаимодействиями) + ограничивающими эти отношения условиями (закон композиции). Во всех объект-системах можно выделить следующие аспекты: 1) первичные элементы, рассматриваемые на данном уровне исследования как неделимые; 2) отношения единства между этими элементами и 3) законы композиции (организации), определяющие границы этих отношений. Понятие о законе композиции, впервые введенное Ю.А.Урманцевым в определение системы, позволяет представить живую систему как закономерный, упорядоченный, неслучайный набор объектов. Отметим, ОТС(У) не дает готового рецепта для нахождения закона композиции системы. Такой закон исследователю необходимо установить самому. Об этом предельно ясно писал А. Пуанкаре: «Логика говорит нам, что на таком-то и таком-то пути мы, наверное, не встретим препятствий; но она же не говорит, каков путь, которорый ведет к цели. Для этого надо видеть цель, а способность, научающая нас видеть, есть интуиция. Без нее геометр был бы похож на того писателя, который безупречен в правописании, но у которого нет мыслей» [по 174, с. 272]. Выявление оптимальных «противоположностей» в системе – вот тот путь, который ведет, по нашему мнению, к установлению законов гармонии рассматриваемого объекта.

Выявление важнейшего аспекта целостности объекта – гармонии - предполагает предварительное изучение его организации. Отметим, лишь во второй половине 20 столетия организация живых систем стала рассматриваться не как некая аксиоматическая данность, не подлежащая изучению, а как нечто самостоятельное, как аспект отдельного исследования. Более того, постепенно стало очевидным, что, как писал лауреат Нобелевской премии Н. Винер [35, с. 43], «главные проблемы биологии...связаны с системами и их организацией во времени и пространстве». Системный подход предполагает сложную организацию всякой живой системы, многообразие взаимодействий между ее элементами. Функционально связанные в одной системе объекты различной сложности образуют последовательность иерархических систем: каждый «сложный» объект состоит из своих «простых» систем, одновременно он же наряду с другими «сложными» объектами включен в более сложную систему в качестве «простого» и т.д. Системный анализ такого рода был использован нами [193, 194, 201] для выявления гармонии систем сердца человека и млекопитающих. Выявление законов организации сложной системы из «простых» позволило приступить к установлению критерия гармонии, согласно которому происходит сопряжение (гармония) «простых» элементов в единое сложное целое. На различных уровнях сложности был произведен анализ сопряжения «простых» сердечных систем, функционально образующих ту или иную «сложную» систему. В результате нами впервые была установлена оптимальная основа сопряжения (гармонии) совокупности «простых» сердечных систем в «сложной» кардиосистеме. Эта универсальная особенность сердечных систем получила обозначение - «принцип оптимального вхождения». Сущность этого принципа заключается в следующем: «Каждая из «простых» сердечных систем, совместно образующих «сложную» кардиосистему, включена в последнюю оптимальным образом, вследствие чего сложная система исполняет свою функцию с минимальным расходом энергии и строительного материала». Возникает вопрос: «Можно ли говорить о присутствии гармонии «противоположностей» в любой сердечной системе, исходя из принципа оптимального вхождения»? Как мы уже отмечали во Введении, ответ положителен, ибо «противоположности» («больше – меньше») «заключены» в каждом сердечном параметре. Любой параметр имеет определенный физиологический диапазон значений, в пределах которого деятельность сердца сохраняется. «Рабочая» величина параметра разделяет этот диапазон на два «противоположных» участка: участок больших и участок меньших возможных значений. По отношению к оптимальной рабочей величине первый из них можно обозначить интервалом «положительных», а второй интервалом «отрицательных» приращений параметра. Оптимальное соотношение «противоположностей» для каждого параметра может быть представлено определенным оптимальным числом.

Отметим, поскольку речь идет о последовательном включении «простых» систем в «сложные», каждому уровню «сердечной» иерархии соответствует своя гармония «противоположностей». При этом сохраняется условие, представленное А.П. Стаховым, чтобы «иерархическая система была устойчивой, каждый ее элемент на любом уровне ее организации должен быть «гармоничным» — это главное положение научной парадигмы, восходящей к Пифагору и Платону» [158]. Таким образом, принцип энергооптимального сопряжения является «гарантом» устойчивости сердечных систем любой сложности.

Глава 2

ЗОЛОТАЯ ГАРМОНИЯ «ПРОТИВОПОЛОЖНОСТЕЙ» В СТРУКТУРАХ СЕРДЕЧНЫХ ЦИКЛОВ

Отметим особенности деятельности сердца, имеющие прямое отношение к содержанию этой главы. Древние философы не сомневались, что целое и две «противоположные» части целого вместе являют собой нераздельную и гармоничную троицу. Деятельность сердца является реальным воплощением этого утверждения. Основу работы сердца составляет периодическая смена двух «противоположных» состояний миокарда - напряжения (систола) и расслабления (диастола). Две «противоположности» объединены в целое - сердечный цикл. Во время систолы происходит изгнание крови из желудочков, в течение диастолы – их наполнение. «Противоположности» в кардиоцикле дополняют друг друга, составляя единое целесообразное целое. Периодическое возобновление кардиоцикла обеспечивает непрерывную работу сердца в качестве мышечного насоса, перекачивающего кровь из вен в артерии.

Нам предстоит ответить на вопросы:

1) можно ли гармонию «противоположностей» в сердечных циклах измерить математическими отношениями?

2) «присутствуют» ли при этом какие-либо «особые» числа?

3) почему «используются» именно эти отношения и числа, а не какие либо другие?

Ответ на эти вопросы представлен в этой главе на основе системного анализа «противоположностей» в структурах сердечных циклов (ССЦ).

2.1. Структуры сердечного цикла в условиях покоя и физической нагрузки

2.1.1. Системное представление структур сердечного цикла (ССЦ)

Структура сердечного цикла (ССЦ) того или иного рассматриваемого нами параметра включает в себя его систолическое и диастолическое значения и их сумму. В каждом кардиоцикле момент перехода систолы в диастолу является временнóй точкой раздела «противоположностей». В нашу задачу входит обосновать математическую гармонию систолической и диастолической «противоположностей» для важнейших сердечных параметров.

Каждую ССЦ согласно общей теории систем Ю.А. Урманцева [180, 181] можно представить в качестве объект-системы. В рассматриваемой объект-системе по Урманцеву необходимо выделить следующие аспекты: 1) первичные элементы, рассматриваемые на данном уровне исследования как неделимые; 2) отношения единства между этими элементами и 3) законы композиции (организации), определяющие границы этих отношений. Рассмотрим «присутствие» этих аспектов в ССЦ. Первичными элементами ССЦ по основанию «противоположностей» является систолическое и диастолическое значения рассматриваемого параметра. Отношением единства между этими элементами является их функциональная связь, а законом композиции ССЦ - математическое выражение определенного вида, объединяющее «противоположные» элементы и их сумму в единое целое. Нами рассмотрены временнáя, объемная, механическая и кровотоковая ССЦ, представляющие важнейшие параметры деятельности сердца. Временнáя ССЦ состоит из длительностей систолы, диастолы и кардиоцикла. Объемная ССЦ включает в себя объем изгнанной крови, объем оставшейся крови и конечнодиастолический (наполненный) объем левого желудочка. Механическая ССЦ представляет собою отнесенные к длительности сердечного цикла среднее систолическое и среднее диастолическое давления в аорте и среднее за сердечный цикл давление в аорте. Кровотоковая ССЦ включает в себя отнесенные к длительности сердечного цикла средний систолический и средний диастолический коронарные кровотоки и средний за кардиоцикл коронарный кровоток. В дальнейшем длительность кардиоцикла и конечнодиастолический объем будут обозначаться как суммарные величины, а среднее за кардиоцикл давление и средний за кардиоцикл коронарный кровоток как средние значения рассматриваемых параметров.

В качестве «возмущающего» внешнего фактора, влияющего на величину параметров сердца, нами избрана кратковременная градуированная мышечная нагрузка. Отметим, что величины одних и тех же сердечных параметров у каждого вида млекопитающих различны и связаны с весом животных. Совокупность всех реально существующих временных, механических, объемных и кровотоковых ССЦ животных различной массы (веса) в пределах физической нагрузки от покоя до максимума составляет некоторое «пространство» ССЦ.

2.1.2. «Пространство» ССЦ млекопитающих

В общем виде для млекопитающих любого n-вида структуру сердечного цикла для всякого j-параметра (j-ССЦ), можно представить выражением:

C_Sj(n_n,W_n) + C_Dj(n_n,W_n) = C_j(n_n,W_n), (2.1)

где n_n, W_n- частота сердцебиений и вес животного n-вида, C_sj(n_n,W_n), C_D_j(n_n,W_n), C_j(n_n,W_n) - систолическое, диастолическое и суммарное значения некоторого j-параметра, соответствующие величинам n_n и W_n. Выражение (2.1) является математическим представлением любой j-ССЦ.

Временную ССЦ каждого животного в соответствии с (2.1) можно представить выражением:

t_S(n_n,W_n) + t_D(n_n,W_n) = T(n_n,W_n), (2.2)

где t_S(n_n,W_n), t_D(n_n,W_n), T(n_n,W_n) – соответственно длительности систолы, диастолы и сердечного цикла животного n-вида при частоте сердечных сокращений n_n. Длительность систолы принята нами равной длительности электромеханической систолы, которая практически равна электрической систоле (см. рис. 2.1). Отметим, что временная ССЦ является «ведущей», определяющей, как будет показано ниже, структуру других сердечных параметров.

Важнейшее значение в организации эффективной деятельности сердца имеет синхронизация «противоположностей» всех рассматриваемых ССЦ. Синхронизация, как природное явление, известна давно. Еще в 17 веке Х. Гюйгенс (1629-1695) обратил внимание на удивительную синхронизацию часов, подвешенных на единое коромысло. Если даже вначале часы шли в разнобой, то через некоторое время у них вырабатывался единый ритм – они начинали работать синхронно. Как установил Гюйгенс, роль синхронизатора в этом случае играли слабые колебания коромысла, на котором подвешивались резонаторы – часы. Два резонатора в общей связующей среде (коромысло) всегда вырабатывали общий ритм в синхронизирующем процессе всей системы как единого целого. Можно привести биологический пример синхронизации. Н. Винер (1894-1964) заметил удивительное поведение светлячков в период весеннего хоровода. В вечерних сумерках деревья были облеплены этими насекомыми. Вначале световые мелькания светлячков были хаотичны. Но спустя некоторое время они становились организованными: множество живых существ синхронно выдавало световые вспышки в едином ритме. Отметим, в основе этого феномена лежит все та же резонансная синхронизация отдельных резонаторов (светлячков) в едином коллективном взаимодействии. В обоих примерах (механическом и биологическом) наблюдаются общие признаки: 1) независимая работа резонаторов (часов, светлячков), 2) наличие активной связующей среды (коромысло, воздух), 3) равноправная работа всех активных начал в едином синхронизированном процессе. Эти признаки являются сугубо функциональными. Они не зависят от природы резонаторов и связующей среды. И в то же время они являются факторами, обусловливающими резонансные основы функциональной гармонии целого. Универсальность явления синхронизации состоит в том, что оно не зависит от вида взаимодействия, не зависит от природы периодически движущихся систем (при этом отсутствует порог синхронизации). Синхронный режим (согласование периодических действий во времени и пространстве) достигается в живой природе при равенстве или соизмеримости частот рассматриваемых действий. При сколь угодно слабых взаимодействиях между элементами динамической системы их взаимное влияние в ходе эволюции обязательно приведет систему в синхронный режим. Добавим к этому, советский математик А.М. Молчанов показал, что «в диссипативных системах резонансы …неизбежны» [109,с. 196]. Эта общность становится фундаментальной при описании резонансных основ функциональной гармонии организма и его систем.

Было показано [217], что в сложных системах, имеющих в основе структуру золотой пропорции, возникают явления, близкие к резонансу. При отклонении от резонансного режима нарушается равновесие, начинают действовать затратные механизмы для поддержания нормального состояния системы. Резонанс, возникающий как следствие «золотой» гармонии «противоположностей», позволяет поддерживать устойчивость структур и процессов сердца с минимальными затратами энергии. С позиций синхронизации В.Н. Трифановым [172] была рассмотрена временная структура сердечного цикла. В режиме функциональной гармонии здесь можно выделить три активных центра, работающих совместно в едином хроноритме. В морфологическом плане – это резонаторы предсердий и желудочков в единой структуре сердца, порождают сердцебиения, в которых систола (два резонатора) и диастола (сердечная ткань) соотносятся между собой по золотой пропорции, и это является признаком нормального (здорового) режима сердцебиений. В функциональном (регуляторном плане) - это восходящие и нисходящие процессы между синусовым узлом и продолговатым мозгом (два резонатора) и возбуждение самого продолговатого мозга (среда). Между этими хронопроцессами в нормальном режиме функционирования устанавливается золотая пропорция, которая реализуется в сердечном ритме через синусовый узел. При резонансе синусовый узел порождает сердечный ритм, при котором систола и диастола миокарда соотносятся между собою по золотой пропорции (доля систолы составляет 38%, доля диастолы – 62% от длительности кардиоцикла). Два сердечных резонатора в равноправном взаимодействии между собой и средой в едином хроноритме создают гармонию, которая характеризуется золотыми «противоположностями». Установлено [57], что аналогичные соотношения между временными «противоположностями» - длительностями систолы и диастолы - имеют место и в предсердиях, и в желудочках. В дальнейшем нами будет показано (см. раздел 2.1.5), что «золотой» частоте сердцебиений соответствует минимальный расход энергии на исполнение деятельности сердца. Кроме того, при резонансе золотых «противоположностей» обеспечивается минимальность затрат энергии на поддержание стабильности сердечных систем.

(Отметим кстати, что К.П. Бутусовым [27] была показана связь золотого сечения с периодами обращения планет Солнечной системы. Было установлено, что Солнечная система находится вблизи максимального резонансного устойчивого состояния, а планеты движутся по орбитам с наименьшей концентрацией космической пыли, т.е. с минимальными затратами энергии.)

Экспериментально показано [285], что в покое у человека и млекопитающих (8 видов), несмотря на значительное различие в размерах и весе, соотношение между длительностью систолы и продолжительностью сердечного цикла определяется аналогичным по форме среднестатистическим выражением:

t_S(n_n,W_n)=k_n,

где k_n – постоянный коэффициент для всего диапазона сердцебиений животных n-вида, W_n – вес животного n-вида. Лепешкин установил, что для различных видов млекопитающих, включая и человека, в покое временнóе соотношение систолы и кардиоцикла находится в пределах 0,42 – 0,46, т.е. приблизительно одинаково. При известном k_n, приравняв t_S(n_n,W_n)/T(n_n,W_n)=0,382, можно для каждого вида определить среднестатистическую «золотую» частоту n_n_ЗС, у которой длительности t_S(n_n_ЗС,W_n), t_D(n_n_ЗС,W_n) и T(n_n_ЗС,W_n) соотносятся по золотой пропорции. Некоторое расхождение реальных частот в покое и вычисленных n_n_ЗС объясняется тем, что лабораторные животные ведут менее активный образ жизни, чем их «вольные» сородичи. Поэтому у лабораторных

Рис. 2.1. Электрокардиограмма человека [193].

Q, R, S, Т, Р - зубцы электрокардиограммы, v –

частота сердцебиений; t_S(ν), t_D(ν), T(ν) - длительность

электрической систолы, диастолы и кардиоцикла при

частоте ν.

животных в покое частота сердцебиений выше «золотой». Отклонение «вверх» от золотого ритма у здоровых особей соответствует степени их детренированности (недостаточность или полное отсутствие регулярной физической нагрузки). Отметим, что у здоровых, физически активных людей и животных частота сердцебиений в покое и «золотая» частота n_n_ЗС практически совпадают (например, для человека n_n_ЗС=63 1/мин [190]).

В дальнейшем будем считать, что в покое у здоровых тренированных особей, ведущих естественный образ жизни, частота n_n_ПОК » n_n_ЗС; эту величину можно рассчитать, используя коэффициент k_n.

Следует отметить, что у каждого i-животного n-вида имеет место «своя» золотая частота n_i_ЗС, которая может несколько отличаться от среднестатистической (n_i_ЗС@ n_n_ЗС). Для отдельного i-животного нами были получены следующие изменения временной структуры кардиоцикла, связанные с изменением частоты сердцебиений n_i по отношению к n_i_ЗС [193]:

t_S(n_i,W_i) = t_S(n_i_ЗС,W_i)/, (2.3)

t_D(n_i,W_i) = t_D(n_i_ЗС,W_i)/()³, (2.4)

T(n_i,W_i) = T(n_i_ЗС,W_i)/(n_i/n_i_ЗС), (2.5)

где W_i – вес i-животного, n_i_ЗС, n_i – «золотая» и другие частоты сердцебиений i-животного, t_S(n_i_ЗС,W_i), t_S(n_i,W_i), t_D(n_i_ЗС,W_i), t_D(n_i,W_i), T(n_i_ЗС,W_i), T(n_i,W_i) – соответственно длительность систолы, диастолы и сердечного цикла при частотах n_i_ЗС и n_i. Среднестатистическая ошибка в выражениях (2.3) и (2.4) во всех случаях не превышала предельной погрешности измерений. Это дает основание считать, что эмпирические выражения (2.3) и (2.4) подобраны правильно.

Таким образом, для любого i-животного при n_i=n_i_ЗС выражение (2.2) можно представить выражением:

t_S(n_i_ЗС,W_i)/ + t_D(n_i_ЗС,W_i)/()³ @ T(n_i_ЗС,W_i)/(n_i/n_i_ЗС). (2.6)

Нас в дальнейшем будут интересовать изменения параметров, связанные с изменением отношения n_i/n_i_ЗС, которое у различных видов млекопитающих изменяется приблизительно в одинаковых пределах. Эти изменения представляет универсальный показатель d =_.n_i/n_i_ЗС. Отметим, что показатель d имеет и другое «содержание». Для каждого животного при заданной физической нагрузке относительные изменения частоты сердцебиений и сердечного выброса за минуту аналогичны, поскольку объем выброшенной крови у млекопитающих за одно сокращение одинаков при любой нагрузке [193, 280, 313]. Следовательно, величину d можно представить в следующем виде:

d= n_i/n_i_ЗС =S(n_i,W_i)/S(n_i_ЗС,W_i),

где S(n_iЗС,W_i,), S(n_i,W_i) – соответственно сердечный выброс за минуту в золотом режиме кровоснабжения и при нагрузке, n_i - частота сердцебиений i-животного при фиксированной нагрузке. Величина d для различных видов животных изменяется приблизительно в одних и тех же пределах (d»1-4) и не зависит от веса и размеров особи. В дальнейшем показатель d будет использоваться нами как универсальный показатель относительного изменения кровоснабжения сердца и всего организма млекопитающих в условиях физической нагрузки. Показатель d=d_ЗС=1 соответствует «золотому» режиму кровоснабжения животных.

Выражение (2.6) приобретает обобщенный вид:

t_S(d_,W_i)/ + t_D(d,W_i)/()³ @ T(d,W_i)/. (2.7)

Выражение (2.7) с учетом «золотого» соотношения «противоположностей»:

0,382T(d_ЗС,W_i)/ + 0,618T(d_ЗС,W_i)/()³ @ T(d_ЗС,W_i)/. (2.8)

В обобщенном выражении (2.8) представлена гармония «противоположностей» во всех временных ССЦ различных видов млекопитающих. При d=d_ЗС=1 выражение (2.8) приобретает «классический» вид «золотой» структуры сердечного цикла:

0,382T(d_ЗС,W_i) + 0,618T(d_ЗС,W_i) = T(d_ЗС,W_i).

Перейдем к анализу механической ССЦ. Показано [139], что по форме кривые артериального давления у человека и различных видов млекопитающих совершенно идентичны (см. рис. 2.2). Этот феномен позволяет нам исключить отдельный анализ этих кривых для различных видов животных.

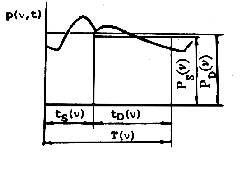
Риc. 2.2. Фазовая структура давления в аорте [190]. ν- частота сердцебиений. t_S(ν), t_D(ν), T(ν) - соответственно длительность электромеханической систолы, диастолы и сердечного цикла; Р_S(ν), P_D(ν), p(ν,t) - соответственно среднее за систолу и среднее за диастолуи мгновенное значения давления в аорте при частоте сокращений v.

Рассмотрим структуру механической ССЦ. Средние за систолу и диастолу величины давления в аорте (см. рис. 2.2):

P_S(n_i_ЗС,W_i) = 1/t_S(n_i_ЗС,W_i),

P_D(n_i_ЗС,W_i) = 1/t_D(n_i_ЗС,W_i),

где P_S(n_i_ЗС,W_i), P_D(n_i_ЗС,W_i) – соответственно среднее за систолу и среднее за диастолу давление, p(n_i_ЗС,W_i,t) – мгновенное значение давления в аорте i-животного при частоте n_i_ЗС.

Среднее за кардиоцикл давление в аорте i-животного в золотом режиме кровоснабжения

= 1/T(n_i_ЗС,W_i).

Анализ кривой давления (см. рис. 2.2), произведенный нами [190], показал, что P_S(n_i_ЗС,W_i) @ P_D(n_i_ЗС,W_i) = . Добавим к этому, что пульсации давления в коронарных сосудах по мере удаления от аорты снижаются. В мышечных артериях пульсации давления уже незначительны, а в микрососудах практически отсутствуют [341]. Это означает, что средние за систолу и диастолу давления в каждом из этих сосудов так же, как и в аорте, равны друг другу. Этот феномен имеет важное значение, поскольку позволяет обеспечить оптимальное крово- и кислородное обеспечение сердечной мышцы и в систолу, и в диастолу (см. раздел 3.4).

Величины среднего систолического и среднего диастолического давлений, отнесенные к длительности сердечного цикла,

= [t_S(n_i_ЗС,W_i)/T(n_i_ЗС,(W_i)],

= [t_D(n_i_ЗС,W_i)/T(n_i_ЗС,(W_i)],

где , - соответственно среднее систолическое и среднее диастолическое давления, отнесенные к длительности сердечного цикла при золотой частоте n_i_ЗС.

Вследствие того, что длительности систолы t_S(n_i_ЗС,W_i) = 0,382T(n_i_ЗС,W_i) и диастолы t_D(n_i_ЗС,W_i) = 0,618T(n_i_ЗС,W_i),

= 0,382, (2.9)

= 0,618. (2.10)

На основе анализа экспериментальных данных, полученных у различных видов млекопитающих в условиях физической нагрузки, в аортальном давлении i-животного происходят следующие изменения [190]:

= n_i/n_i_ЗС, (2.11)

= , (2.12)

= , (2.13)

где , - соответственно среднее по отношению к длительности кардиоцикла систолическое и диастолическое давления, - среднее давление в аорте i-животного при частоте n_i. Выражения (2.11) - (2.13) установлены при анализе экспериментальных данных, полученных у нескольких видов млекопитающих. Произведенный анализ выражений (2.11) - (2.13) показал, что среднестатистическая ошибка этих выражений не превышает предельной погрешности измерений. Отметим, что относительному изменению среднего давления в аорте соответствует одинаковое относительное изменение среднего давления на каждом сосуде [247].

Исходя из (2.9)-(2.13) и заменив n_i/n_i_ЗС на d, получим математическую структуру механической ССЦ в условиях покоя и нагрузки:

0,382 + 0,618 @ . (2.14)

В (2.14) представлена гармония «противоположностей» механической ССЦ в золотом режиме и при физической нагрузке. При d=d_ЗС=1 закон (2.14) представляет «золотую» структуру «противоположностей»:

0,382 + 0,618 = .

Рассмотрим математические особенности сопряжения «противоположностей» объемной ССЦ в условиях покоя и физической нагрузки. Предварительно отметим, что кривые сердечного выброса у различных видов млекопитающих совершенно идентичны [266, 267]. Эта аналогия позволяет нам не рассматривать особенности объемной ССЦ для отдельных видов млекопитающих.

Для объемной ССЦ среднее систолическое значение за сердечный цикл соответствует объему крови, изгнанной из левого желудочка за одно сокращение, среднее диастолическое значение за сердечный цикл равно объему оставшейся крови и суммарное значение - конечнодиастолическому объему. Экспериментально показано [207, 266, 267], что в покое (n_i=n_i_ЗС) у человека и различных видов млекопитающих с разницей в весе в 1500 раз соотношение величин , и практически совпадает с золотой пропорцией:

0,382 + 0,618= .

Это выражение представляет золотую гармонию «противоположностей» объемной ССЦ.

Установлено [271, 280], что при различной мышечной нагрузке объем крови, изгнанной за одно сокращение, постоянен. С другой стороны, показано, что чем больше нагрузка, тем в большей степени уменьшаются размеры желудочков [237, 315, 361]. В условиях физической нагрузки [190]:

=, (2.15)

= /(), (2.16)

= /, (2.17)

где , , - соответственно среднее систолическое, среднее диастолическое и суммарное (конечнодиастолическое) значения объема левого желудочка i-животного, отнесенные к длительности кардиоцикла, в золотом режиме и при физической нагрузке.

При учете (2.3) – (2.5) и (2.15) – (2.17) и замене n_i/n_i_ЗС на d получим обобщенный закон объемной ССЦ:

0,382 + 0,618/d² @ /d. (2.18)

В (2.18) представлена гармония систолической и диастолической «противоположностей» объемной ССЦ в условиях покоя и нагрузки.

Рассмотрим особенности кровотоковой ССЦ в условиях покоя и нагрузки. Форма пульсаций кровотока в крупных коронарных артериях аналогична [311; 347]. Установлено [320], что соотношения между значениями коронарного кровотока в характерных точках кардиоцикла не меняются при любом уровне нагрузки. Отмеченные особенности позволяют нам рассматривать общий коронарный кровоток, не рассматривая кровотоки в отдельных артериях.

Средние величины коронарного кровотока за систолу и диастолу в золотом режиме кровоснабжения:

Q_S(n_i_ЗС,W_i) = 1/t_S(n_i_ЗС,W_i),

Q_D(n_i_ЗС,W_i) = 1/t_D(n_i_ЗС,W_i),

= 1/T(n_i_ЗС,W_i)

где Q_S(n_i_ЗС,W_i), Q_D(n_i_ЗС,W_i) – соответственно средний за систолу и средний за диастолу кровотоки, - средний за кардиоцикл кровоток, q(n_i_ЗС,W_i,t) – мгновенное значение кровотока i-животного при золотой частоте n_i_ЗС. Отметим, что пульсации кровотока в коронарных сосудах по мере удаления от аорты заметно снижаются; в мышечных артериях и микрососудах средние кровотоки в систолу и диастолу отличаются незначительно [341]. Следовательно, во всех мышечных и терминальных сосудах Q_S(n_i_ЗС,W_i)=Q_D(n_i_ЗС,W_i)=.

Средние величины систолического и диастолического кровотоков, отнесенные к длительности сердечного цикла:

= [t_S(n_i_ЗС,W_i)/T(n_i_ЗС,W_i)],

= [t_D(n_i_ЗС,W_i)/T(n_i_ЗС,W_i)],

где , - соответственно средний систолический и средний диастолический кровотоки, отнесенные к длительности кардиоцикла i-животного при золотой частоте n_i_ЗС.

Исходя из (2.3) – (2.5),

= 0,382, (2.19)

= 0,618[. (2.20)

Качественная сторона гемодинамических изменений в коронарном русле во время физической нагрузки достаточно хорошо изучена. Рассмотрим некоторые данные, полученные в условиях нагрузки. Установлено, что при любой фиксированной мышечной нагрузке относительные изменения кровотоков к их величинам в покое одинаковы во всех ветвях левой коронарной артерии [280, 347] и эндо- и эпикардиальных слоях сердечной мышцы [229]. Не меняется отношение среднего кровотока в коронарном синусе к среднему коронарному кровотоку в левой коронарной артерии при изменении давления в аорте [282] и сжатии легочной артерии [309]. Отметим, что средний коронарный кровоток и минутный выброс сердца в покое и при нагрузке связаны между собою постоянным соотношением 0,04-0,05, одинаковым для человека и млекопитающих [189, 317]. Как было представлено нами выше, объем крови, изгнанной за одно сокращение сердца, постоянен при любой нагрузке. Следовательно, средний коронарный кровоток при нагрузке возрастает при частоте n_i в n_i/n_i_ЗС раз. Очевидно, что во всех крупных, мелких и средних коронарных артериях средний кровоток при нагрузке возрастает в n_i/n_i_ЗС раз. Как следствие этого феномена, анализ относительных изменений в одной из коронарных артерий, полученных при нагрузке, позволяет получить представление об аналогичных изменениях общего среднего кровотока. В условиях физической нагрузки по отношению к золототому режиму кровоснабжения сердца составляющие кровотоковой ССЦ изменяются следующим образом [190]:

= (n_i/n_i_ЗС)^3/2, (2.21)

= , (2.22)

= n_i/n_i_ЗС. (2.23)

Исходя из (2.3) – (2.5), (2.21) – (2.23) и заменив n_i/n_i_ЗС на d, получим обобщенный математический закон композиции кровотоковой ССЦ млекопитающих в условиях покоя и физической нагрузки:

0,382d³+ 0,618d @ d². (2.24)

В (2.24) представлен математический закон сопряжения «противоположностей» кровотоковой ССЦ. В условиях покоя, когда d=d_ЗС, (2.24) приобретает классическую «золотую» форму «противоположностей»:

0,382+ 0,618 @ .

Обобщим законы (2.8), (2.14), (2.18) и (2.24). В золотом режиме общий закон композиции всех рассматриваемых ССЦ можно представить обобщенным выражением:

0,382 + 0,618 = , (2.25)

где - среднее за кардиоцикл (суммарное) значение j-параметра i-животного в золотом режиме кровоснабжения организма.

Для средних (суммарных) значений j-параметров различных видов млекопитающих экспериментальным путем получены среднестатистические зависимости от веса i-животного [190, 264, 265, 284, 299; 327-329]:

=a_jW_i^b_j, (2.26)

где a_j, b_j - величины, соответствующие j-параметру сердца (эти величины имеют постоянное значение независимо от веса животных). С учетом (2.25) – (2.26), выражение (2.25) приобретает вид:

0,382a_jW_i^b_j + 0,618a_jW_i^b_j= a_jW_i^b_j. (2.27)

В выражении (2.27) «присутствует» «золотая» пропорция:

a_jW_i^b_j: 0,618a_jW_i^b_j = 0,618a_jW_i^b_j: 0,382a_jW_i^b_j= 1,618…

Естественно, изменением веса животных в течение кратковременной мышечной нагрузки можно пренебречь. С учетом (2.26) и представленных выше зависимостей (2.8), (2.14), (2.18) и (2.24), влияние физической нагрузки на величину систолических, диастолических и суммарных элементов ССЦ представлено нами в обобщенном законе [193]:

0,382+0,618@, (2.28)

где k_j - величина, соответствующая j-параметру (эта величина не зависит от уровня физической нагрузки и веса животных). Естественно, что при d=d_ЗС=1 выражение (2.28) предстает в виде (2.27). Отметим, что относительное расхождение между левой и правой частями приблизительного тождества (2.28) в заданных пределах (δ = 1¸4) составляет не более (-3 - +7)%, причем расхождение в 7% соответствуют верхнему уровню нагрузки. Отметим, что расхождение (-3 - +7)% находится в пределах ±(5-6)%-отклонения параметра от оптимального значения, при которых оптимальность системы еще сохраняется [23]. Закон (2.28) с достаточной точностью отображает реальные соотношения между «противоположностями» во всех ССЦ. В (2.28) представлен обобщенный математический закон композиции «пространства» (системы) временных, механических, объемных и кровотоковых ССЦ различных видов животных в условиях покоя и физической нагрузки.

Рассмотрим последовательность «сопряжения» принципа оптимального вхождения и гармонии «противоположностей» в законе (2.28). Первым этапом «сопряжения» является «подбор» оптимальной величины среднего (суммарного) значения j-параметра по отношению к весу i-животного. «Противоположности» на этом «этапе» представлены участками «положительных» и «отрицательных» приращений относительно оптимальной «рабочей» величины параметра. На втором этапе происходит «подбор» оптимального соотношения «противоположностей» (систола - диастола) для среднего (суммарного) значения j-параметра. Первый этап сопряжения гармонии «противоположностей» и принципа оптимального вхождения представлен постоянными величинами a_j и b_j; второй связан с числами 0,382 и 0,618. Отметим, вторая стадия сопряжения соответствуют золотому режиму кровоснабжения сердца. При «возмущении» организма физической нагрузкой «появляются» новые числа. Происходит «подбор» оптимальной средней величины каждого j-параметра в соответствии с уровнем нагрузки d. Среднее значение j-параметра разделено на «противоположности» (систола - диастола) в соответствии с величиной d. При нагрузке оптимальное вхождение j-«противоположностей» представлено числами k_j, k_j+1 и k_j-1 и величиной d.

Табл. 1. Постоянные j-величины «пространства» ССЦ

j-ССЦ	j-коэффициенты
j-ССЦ	a_j	b_j	k_j
Временная	0,249	0,250	-2
Механическая	1,47×10⁵	0,033	1
Объемная, мл	1,76	1,02	-1
Кровотоковая	7,48	0,81	2

Примечание. Во всех расчетах по (2.28) временная, механическая, объемная и кровотоковая ССЦ соответственно имеют размерность сек, дн/см², мл, мл/мин, [W_i] - кг.

Таким образом, сопряжение принципа оптимального вхождения и гармонии оптимальных «противоположностей» на всех этапах построения «пространства» (2.28) имеет математическую базу. Величины 0,382, 0,618, a_j, b_j, k_j, k_j+1, k_j-1 и диапазон d=1÷4 образуют числовой каркас «пространства» всякого i-животного (2.28). Эти «особые» числа постоянны для различных видов млекопитающих независимо от их вида и размеров [193]. Таким образом, в «особых» числах представлена математическая основа оптимальной композиции «пространства» ССЦ. Отметим, что универсальные золотые числа 0,382 и 0,618 «присутствуют» во всех j-параметрах. Величины a_j, b_j, и k_j представлены в Табл. 1.

Следует обратить внимание на еще одну особенность деления j-ССЦ при нагрузке. В покое «вхождение» «противоположностей в j-ССЦ представлено «чистыми» золотыми числами, а при нагрузке – золотыми числами + определенными отклонениями для каждого d. Экспериментально показано (см. раздел 2.1.5), что и при отклонениях «противоположностей» от пропорции золотого сечения имеет место экономия энергии, максимальная для данного уровня нагрузки. Поэтому все «противоположности» в диапазоне d=1÷4 можно условно считать «золотыми», поскольку они имеют в своей основе «чистое» золотое сечение + оптимальные отклонения от последнего.

2.1.3. «Золотые» особенности гармонии, симметрия и резонанс

в «пространстве» ССЦ

Обобщенный закон (2.28) можно представить в следующем виде:

[0,382+ 0,618)] @ .

Очевидно, что в пределах нагрузки основу гармонии «противоположностей» для каждой j-ССЦ различных животных составляет приблизительное тождество:

0,382+ 0,618@ 1. (2.29)

Диапазон d=1-4 представляет «рабочий» интервал величины d, в котором сохраняется энергооптимальное соотношение между «возможностями» сердечно-сосудистой системы организма и допустимыми пределами физической нагрузки.

Первый член (2.29) представляет долю систолической «противоположности» j-параметра:

n_S(d) = 0,382, (2.30)

а второй – долю диастолической (см. рис. 2.3),

n_D(d) = 0,618. (2.31)

В (2.29) представлена основа гармонии «противоположностей» в ССЦ сердечных параметров в покое и при различных уровнях нагрузки. Величины n_S(d) и n_d(d) являются мерой «противоположностей», представляющих энергооптимальную гармонию для всех животных.

а второй – долю диастолической (см. рис. 2.3),

n_D(d) = 0,618. (2.31)

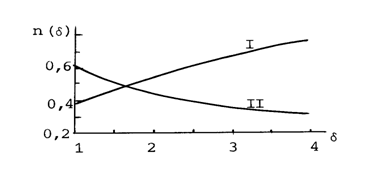
Рис. 2.3. Золотые «противоположности» j-ССЦ [193].

Кривые I и II представляют значения n_S(d)=0,382 и n_D(d)= 0,618.

В выражении (2.29) присутствует аспект симметрии. Ю.А. Урманцев дает следующее определение симметрии: «Симметрия – это категория, обозначающая сохранение признаков П объектов О относительно изменений И» [180, с. 195]. Каждому j-параметру всех животных при уровне нагрузки d соответствуют аспекты симметрии: инвариантные величины n_S(d) и n_D(d) (см. рис. 2.3). В пределах d=1-4 преобразование j-ССЦ i-животного в аналогичные j-ССЦ особей других видов происходит с «использованием» «своего» j-закона преобразования [194]; этот закон неизменен при любом значении d. Таким образом, в выражении (2.29) представлена математическая связь между принципом оптимального вхождения, гармонией «противоположностей» и симметрией «тиражирования» j-ССЦ для различных видов млекопитающих.

Отметим, что в (2.29) –(2.31) и рис. 2.3 «представлены» также изоморфные преобразования ССЦ. Согласно Ю.А. Урманцеву, изоморфизм двух или нескольких множеств заключается в том, что между их элементами по какому-либо закону существует взаимно-однозначное соответствие. ССЦ различных параметров i-животного можно по определенным законам «пересчитать» друг в друга [194]. Этот феномен обеспечивает синхронизацию сердечных циклов важнейших параметров i-животного при любой величине d. Таким образом, в выражениях (2.29) - (2.31) и рис. 2.3 отражена «золотая» основа синхронизации 4 типов сердечной ритмики, что обеспечивает согласованную деятельность систем сердца как в покое, так и при нагрузке. Особенности изоморфных преобразований внутри «пространства» (2.28) подробно рассмотрены нами в книге [194].

При замене на х и умножении правой части на х⁰ =1 (2.29) можно представить в следующей форме:

0,382х + 0,618х^-1 @ х⁰. (2.31)

В выражении (2.31) следует отметить интересные особенности:

1. В структуре (2.31) «переплетаются» геометрические прогрессии: 1) Ф^-2, Ф^-1, Ф⁰ и 2) х^-1 , х⁰ , х. Первая прогрессия, «золотая», представляет гармонию сердечных «противоположностей» при покое организма. Вторая «переплетена» с числами 0,382 и 0,618 в условиях нагрузки. «Переплетение» двух прогрессий обусловливает энергооптимальную гармонию «противоположностей» в условиях покоя и в физиологических пределах нагрузки [194].

2. Отношение х_max/х_min =2 имеет характерную особенность: оно соответствует отношению верхнего и нижнего значений двух соседних октав . Это соотношение соответствует двум интервалам качественной симметрии [105]. Таким образом, композиция (2.31) связана с золотым числом Ф и числом 2, которое наряду с «особыми» числами p и e имеет широкое «представление» в законах физики [2].

Отметим, что диапазон d=1-4 представляет интервал нагрузки, в которых существует оптимальность «противоположностей» в структурах сердечных циклов. Классическая золотая пропорция и оптимальные отклонения от нее позволяют нам говорить об этом диапазоне как интервале существования золотой гармонии.

2.1.4. Вес животных и энергооптимальность средних значений параметров сердца

В нашу задачу входит показать оптимальность величин рассматриваемых параметров по отношению к весу животных.

Прежде всего, следует отметить оптимальность веса (массы) тела млекопитающих. И.Ф. Образцов и М.А. Ханин [113] показали, что наблюдаемые в природе веса тел млекопитающих весьма близки к оптимальным величинам, допустимым с точки зрения энергетики. Зависимость суммарных значений j-параметров от веса животных представлена нами обобщенным выражением (2.3). Покажем, что в покое суммарные (суммарные) значения рассматриваемых параметров (среднее артериальное давление, средний коронарный кровоток, длительность кардиоцикла и конечнодиастолический объем левого желудочка) энергооптимальны по отношению к весу млекопитающих.

Оптимальная энергетика сердца определяется сопряжением «противоположностей» двух параметров: 1) артериальное давление и 2) воспроизводство эритроцитов [113]. При увеличении артериального давления уменьшается объем циркулирующей крови и, следовательно, энергетические затраты, связанные с эритропоэзом. С другой стороны, при этом возрастает механическая работа сердца и увеличивается масса сердца. Природа нашла оптимальное соотношение между затратами мощности на воспроизводство эритроцитов и мощности, потребляемой сердцем, при котором их сумма равна минимальной величине. Вес сердца в этом случае оптимален, т.е. имеет минимально возможную величину. Таким образом, веса сердца и организма соотносятся между собою оптимальным образом; это отношение является инвариантным для различных видов животных и приблизительно равно 0,06 [304, 328].

Установлено [113, 185], что в покое среднее артериальное давление и минутный выброс сердца оптимальны по отношению к массе (весу) организма животных. Эти параметры оптимальны с точки зрения минимальности энергозатрат на кровоснабжение организма. Средний коронарный кровоток и минутный выброс сердца связаны между собою отношением 0,04-0,05, одинаковым и в покое и при нагрузке для всех млекопитающих [189, 317]. Было показано [193, 194, 202], что в покое среднее давление в аорте и средний коронарный кровоток имеют оптимальные значения. Таким образом, очевидно, что и коронарный кровоток оптимален по отношению к весу животных.

В покое естественный объем изгнанной крови за одно сокращение (ударный объем) по отношению к конечнодиастолическому (полному) объему левого желудочка составляет энергооптимальную долю [333]. Минутный сердечный выброс и ударный объем оптимальны по отношению к весу. Следовательно, оптимальна по отношению к весу и частота сокращений (сердцебиений), а, следовательно, и длительность сердечного цикла.

Таким образом, суммарные значения рассматриваемых j-параметров в золотом режиме энергооптимальны по отношению к весу отдельных животных. Поскольку и вес, и суммарные значения j-параметров оптимальны, то, очевидно, что «подбор» чисел a_j и b_j «неслучаен». Эти числа представляют оптимальное соотношение между весом организма и величиной того или иного сердечного j-параметра в золотом режиме кровоснабжения организма.

В «незолотых» режимах кровоснабжения организма все представленные j–параметры сердца также имеют энергооптимальную «основу». Установлено, что при нормальных условиях сердце млекопитающих в покое [240, 296] и при любой физической нагрузке [263/ исполняет свою функцию с минимально возможными затратами энергии. Показано [193, 194], что расход механической энергии на изгнание единичного объема крови из желудочков оптимален при любом уровне нагрузки. За физиологическими пределами работа сердца невозможна, т. к. при этом нарушается адекватное кровоснабжение организма. Оптимальная деятельность сердца обеспечивается лишь в пределах диапазона d=1-4. Следует отметить, что чем больше d, тем менее экономична работа сердца [193, 194]. Тем не менее, каждому значению d соответствует «свой» оптимальный режим работы сердца. Золотое сечение представляет наиболее экономное, с точки зрения энергетики, сопряжение «противоположностей» в сердечном цикле млекопитающих.

2.1.5. Энергооптимальность «противоположностей» ССЦ в условиях нагрузки

Следует отметить важное обстоятельство: в каждой сердечной системе присутствуют «противоположности» («больше» - «меньше»). Это обусловлено тем, что любой параметр имеет определенный физиологический диапазон поиска, в пределах которого деятельность сердца сохраняется. «Рабочая» величина каждого параметра разделяет диапазон на два «противоположных» участка: участок «положительных» и участок «отрицательных» приращений параметра. «Положительный» и «отрицательный» участки диапазона согласно ОТС Урманцева можно представить как неделимые элементы системы. С другой стороны, в соответствии с принципом оптимального вхождения «положительный» и «отрицательный» участки являются «простыми системами», образующими «сложную» систему (диапазон значений параметра). Таким образом, принцип оптимального вхождения представляет одновременно сопряженный поиск оптимальной гармонии «противоположностей» во всех простых системах и оптимальную сборку «сложного» из «простого».

Показано [194-197], что в покое реально всегда «работает» энергооптимальное значение параметра. При переходе от покоя к внешнему «возмущающему» фактору происходит поиск новых «рабочих» значений каждого параметра внутри диапазона допустимых величин за счет смещения либо в сторону увеличения (положительное приращение), либо в сторону уменьшения (отрицательное приращение). В результате «внутри» диапазона возможных значений параметра должно устанавливается новое соотношение «положительной» и «отрицательной» «противоположностей». «Внутри» каждой ССЦ при изменении «возмущения» изменяется соотношение между «противоположностями» за счет смещения момента перехода из систолы в диастолу. Эффективность работы сердца принято определять как отношение производимой сердцем механической работы к потребляемой химической энергии. Оптимальной композицией ССЦ при физической нагрузке должна быть такая композиция, при которой исполнение функции сердца сопряжено с минимально возможным для заданного уровня нагрузки расходом энергии.

Покажем, что энергооптимальность суммарных (средних) значений рассматриваемых параметров всегда имеет место при сердечном ритме, естественном для данного режима нагрузки. Показано, что при нагрузке и минутный выброс [113], и ударный объем [296] энергооптимальны. Естественно, что для любого уровня нагрузки оптимальна и длительность естественного сердечного цикла и соотношение «противоположностей» во временной ССЦ.

Рассмотрим оптимальность «вхождения» систолической и диастолической «противоположностей» в структуры сердечных циклов. Предварительно отметим, что между утилизацией кислорода и потреблением энергии в сердечной мыщце существует линейная зависимость [245]. Измерение объема потребленного кислорода и механической работы сердца позволяет определить эффективность работы последнего. Установлено [283, 349], что при искусственном увеличении сердечного ритма при электрической стимуляции потребление кислорода возрастает (минимальное значение при естественной частоте сердцебиений). Следует при этом отметить, что в пределах электрической стимуляции механическая работа интактного сердца остается неизменной и равной естественной величине до начала стимуляции [228, 239]. При электрической стимуляции временная структура сердечных циклов соответствует их естественным аналогам [8]. Таким образом, эффективность работы сердца максимальна при естественном, найденном природой ритме; каждый естественный ритм оптимален к «своему» уровню нагрузки. Таким образом, естественное изменение сердечного ритма при нагрузке во всех временных ССЦ соответствует энергооптимальному соотношению «противоположностей».

Давление в аорте можно менять за счет вариации периферического давления (эффект Анрепа), сохраняя при этом естественный уровень кровоснабжения организма и частоту сердцебиений. При этом установлено [315], что минимальное потребление кислорода сердечной мышцей имеет место при естественном среднем давлении в аорте и, следовательно, при естественном соотношении его систолической и диастолической составляющих. Следовательно, в условиях каждого уровня нагрузки минимальный расход химической энергии имеет место при соотношении «противоположностей» в механической ССЦ, естественном для этого уровня нагрузки.

Сравним изменения работы сердца по изгнанию крови и работы на перфузию сердечной мышцы за минуту при возрастании частоты электрической стимуляции. Первая работа остается неизменной, в то время как вторая возрастает за счет увеличения среднего коронарного кровотока [112, 283, 349]. Очевидно, что минимальная работа по перфузии коронарных сосудов имеет место тогда, когда электроритм совпадает с естественным ритмом. Следовательно, минимальные затраты энергии на перфузию сердца для всякого уровня физической нагрузки соответствует естественной гармонии «противоположностей» кровотоковой ССЦ.

Показано [334], что искусственно регулируемая работа по заполнению левого желудочка с последующим изгнанием постоянного объема крови при постоянном сердечном ритме и среднем давлении в аорте сопровождается минимальным потреблением «сердечного» кислорода в том случае, когда соотношение «противоположностей» (объем изгнанной и оставшейся крови в желудочке) равно естественному. Следовательно, при всякой нагрузке минимальные затраты энергии на изгнание ударного объема крови из желудочков имеют место при естественной гармонии «противоположностей» объемной ССЦ.

Таким образом, в итоге можно сказать, что всякая j-ССЦ «пространства» (2.28) имеет своего рода иерархию оптимальностей: 1) за счет оптимальности ее суммарной величины по отношению к нагрузке и 2) за счет оптимального соотношения между ее систолической и диастолической «противоположностями». Несомненно, что обе «оптимальности» состоят в непрерывном сопряжении между собой. За счет этих факторов обеспечивается наиболее экономная работа сердца млекопитающих. Минимальные затраты энергии на обеспечение адекватного кровоснабжения организма млекопитающих имеют место в том случае, когда композиции временной, механической, объемной и кровотоковой ССЦ (и, по-видимому, других!) в покое и нагрузке соответствуют их естественным аналогам. Очевидно, что гармония «противоположностей» во всех ССЦ «подобрана» Природой таким образом, что именно при таком «раскладе» (и никаком другом!) общий расход энергии, расходуемой на функционирование сердца, достигает минимума. Показано теоретически и экспериментально [239], что при нормальных физиологических условиях КПД сердца максимален и составляет 18-20%.

Энергоптимальное сопряжение «противоположностей» в ССЦ в покое и при нагрузке обусловлено золотым сечением и его замечательными свойствами. Очевидно, что принцип оптимального вхождения является критерием гармонии всех ССЦ, составляющих «пространство» (2.28). Неизменная экономия энергии, сопутствующая оптимальному «вхождению» каждой ССЦ в «пространство» (2.28) является условием энергооптимальной гармонии всего «пространства».

Необходимо отметить еще одну особенность «пространства» (2.28). Принцип наименьшего действия имеет в своей основе «решение», наиболее экономное из всех возможных. Этот феномен представлен во всех разделах физики (см. раздел 1.4). Принцип наименьшего действия в каждом конкретном случае дает столько уравнений, сколько имеется независимых координат. В выражении (2.28) мы имеем «пространство» четырех параметров; структура каждого из них может быть представлена множеством соотношений «противоположностей». Однако организм неизменно «предпочитает» самые экономичные из них. Таким образом, «присутствие» принципа наименьшего действия имеет место и в биологическом объекте – сердце млекопитающих.

2.2. Гармония и «эстафета» золотых «противоположностей» в сердечных процессах

Прежде, чем перейти к представлению «эстафеты» золотых «противоположностей» в сердечных объектах, рассмотрим последовательность золотых чисел: Ф⁰, Ф¹; Ф²; Ф³; …, Фⁿ^-2, Фⁿ^-1, Фⁿ,… Очевидно, что эту последовательность можно продолжать до бесконечности. Любые три соседних числа одновременно представляют собой геометрическую прогрессию, в которой всякое число ряда больше предыдущего в 1,618 раз:

Фⁿ⁺¹: Фⁿ = Фⁿ⁺² : Фⁿ⁺¹ = 1,618…,

и аддитивный рекуррентный ряд чисел, в котором каждое число равно сумме двух предыдущих,

Фⁿ+ Фⁿ⁺¹ = Фⁿ⁺².

Очевидно, что свойства геометрической прогрессии и рекуррентности сохраняются для всякого другого «золотого» ряда:

AФ⁰, AФ¹; AФ²; AФ³; …, AФⁿ, AФⁿ⁺¹, AФⁿ⁺²,… (2.32)

где А может иметь любую величину и размерность (см, см³, сек, г, кал и т.д.). Двигаясь слева направо от АФ⁰, получаем последовательность, которую можно обозначить как восходящий ряд золотых чисел. При перемещении в обратном направлении от АФ⁰ получаем нисходящий ряд золотых чисел:

AФ⁰, AФ^-1; AФ^-2; AФ^-3; …, AФ^-ⁿ, AФ^-(ⁿ⁺¹⁾, AФ^-(ⁿ⁺²⁾,… (2.33)

Ряд золотых чисел по (2.33) представлен нами в последовательности преобразований световой энергии в растительных и животных клетках [199, 342]. Ниже нами будет рассмотрено «присутствие» восходящего ряда золотых чисел в сердечных процессах.

Напряжение мышечных волокон миокарда в течение систолы разделяется на ряд активностных состояний (рис. 2.4): 1) асинхронное напряжение (0-1), 2) синхронное напряжение (1-2), 3) сокращение (2-3). Соответственно, 0-3 – длительность систолы, 0-4 – длительность кардиоцикла. Временной сегмент (0-2) соответствует подготовке к изгнанию крови из желудочков, он включает в себя противоположные формы напряжения волокон при неизменной длине.

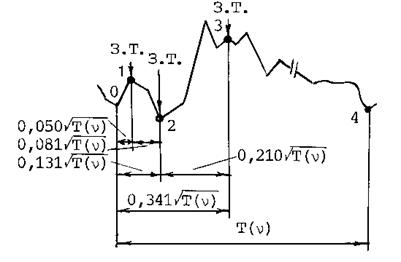
Рис. 2.4. «Золотая» динамокардиограмма человека. [190]. υ - частота сердцебиений; T(υ) – длительность сердечного цикла при частоте υ.

З.Т. –«золотые» точки интервалов 0-2 (т. 1), 0-3 (т. 2) при частоте υ. «Золотая» точка Т. 3 делит сердечный цикл 0-4 по золотому сечению только при υ= υ_ЗС.

С активностной точки зрения интервалы (0-1) и (1-2) соответствуют «противоположностям»: беспорядочное и синхронное напряжение волокон. Сегмент (2-3) соответствует времени изгнания крови из желудочков; этот сегмент соответствует укорочению сердечных волокон. Сегмент 0-3 (интервал подготовки + интервал изгнания) включает в себя две «противоположности»: постоянство и изменение длины мышечных волокон. Для человека интервал асинхронного напряжения, интервал синхронного напряжения, фаза напряжения при неизменной длине мышечных волокон, интервал сокращения и длительность систолы соответственно равны [6; 7, 190]: 0,050, 0,081, 0,131, 0,210, 0,340, где n - частота сердцебиений, T(υ) - длительность сердечного цикла, соответствующая частоте n.

Е.Б. Бабский и В.Л. Карпман, установившие данные математические соотношения, не заметили «присутствия» в них золотых чисел. Однако очевидна аналогия «восходящего» ряда длительностей восходящему ряду золотых чисел (2.32). Временной интервал напряжения при постоянной длине сердечных волокон составляют длительности «противоположных» интервалов асинхронного и синхронного напряжения:

0,131: 0,081= 0,081 : 0,050 = 1,62. (2.34)

Аналогично систолу в целом можно также представить золотой пропорцией

0,340 : 0,210 = 0,210 : 0,131 = 1,62. (2.35)

В (2.34) и (2.35) представлена своего рода эстафета «временных» золотых сечений по всей систоле в соответствии с восходящим рядом (2.11): 0,050, 0,081, 0,131, 0,210, 0,340. Поскольку при нагрузке общая длительность систолы t_S(n) = t_S(n_ЗС)/, то, очевидно, что все составляющие систолы изменяются аналогичным образом. Следовательно, «золотая» гармония между «противоположностями» в течение систолы не зависит от длительности сердечного цикла и сохраняется при любой частоте сердцебиений. Отметим, что «золотая» гармония «противоположностей» между систолой в целом и диастолой имеет место только при золотом сердечном ритме (ν=ν_ЗС).

Показано [9], что организация временной структуры работы здорового сердца по золотому сечению соответствует минимуму энергии, затрачиваемой сердцем на изгнание крови. Известно [82], что сердечная мышца закручена по золотой логарифмической спирали с углом 22-25^о. «Золотая» последовательность интервалов закрутки в течение систолы обеспечивает максимальную силу сокращения. В. А. Добрых [58, 59] показал, что при экстрасистолии отношение интервала сцепления к продолжительности предэктонического кардиоцикла, близко к пропорции золотого сечения. Автор высказал мнение, что золотые сечения являются своеобразными «островками» устойчивости динамических систем, обеспечивающими стационарный режим их существования.

Рассмотрим эстафету «объемных» золотых «противоположностей», которая имеет место в точках «качественного» перехода при наполнении и опорожнении предсердий и желудочков. Показано [338], что за интервал раннего наполнения в левое предсердие человека поступает 37%, а в фазу позднего наполнения - 63% от общего количества крови, поступившей в предсердие за интервал закрытого митрального клапана; это соотношение практически соответствует золотому сечению. Границей раздела «противоположных» состояний (раннего и позднего наполнения) служит момент, в который прекращается падение и начинается рост давления в левом предсердии. Установлено [342], что максимальный и минимальный объем обоих предсердий и их разность в течение сердечного цикла также приблизительно составляют золотую пропорцию. Через открытый митральный клапан в течение времени, когда предсердие представляет собою трубку, открытую с двух сторон, в левый желудочек поступает приблизительно 60% крови от общего количества, а остальные 40% - в течение систолы предсердия [261]. Соответственно, фазу изгнания крови из желудочков можно также разделить на два «противоположных» периода: возрастающего и редуцированного изгнания. Объемы выброшенной крови за эти интервалы соотносятся по пропорции золотого сечения [193]. Следует напомнить, что в покое отношение объема изгнанной крови, объема оставшейся крови и конечнодиастолического объема желудочков приблизительно соответствует золотой пропорции [207, 266, 267]. Итак, в золотом режиме кровоснабжения организма «объемная» картина наполнения и опорожнения предсердий и желудочков, представленная с учетом «противоположностей» в этих процессах, неизменно связана с пропорцией золотого сечения. Установленные соотношения позволяют представить процесс наполнения и опорожнения предсердий и желудочков как гармонию золотых «противоположностей». Этот процесс имеет энергооптимальную основу [193, 194]. Добавим к этому, что отток «сердечной» крови осуществляется преимущественно через венозный синус в правом предсердии, куда сбрасывается примерно 2/3 питающей сердце крови, а остальная кровь оттекает по сердечным венам и тебезиевым сосудам. Таким образом, и отток венозной крови сердца «по противоположностям» происходит в соответствии с числами Фибоначчи: (1:2)!

В момент замыкания полулунного клапана давление в аорте составляет 62% от максимального [193, 207] (рис. 2.6). Разность между максимальным и минимальным значениями в аорте называется пульсовым давлением. Соотношение между пульсовым, минимальным и максимальным давлениями в аорте соответствует золотому сечению; это соотношение сохраняется при любом уровне физической нагрузки [193, 194] (рис. 2.6). Величины среднего давления в аорте равны энергооптимальным значениям во всех режимах нагрузки [193, 194]. Следовательно, золотая гармония максимального, минимального и пульсового давлений в аорте имеет в своей основе золотое сечение. Отметим еще одну «золотую» особенность кривой артериального давления в покое: у здоровых людей среднее артериальное давление делит пульсовое давление DP (см. рис. 2.6) по золотой пропорции [63]. Установлено [350], что естественной форме кривой давления в аорте соответствует минимальная мощность, необходимая для выброса единичного объема крови.

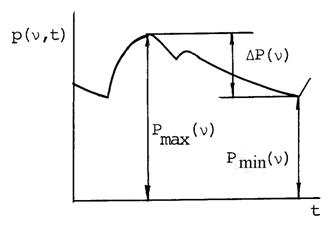
Рис. 2.6. Кривая давления в аорте. υ - частота сердцебиений; p(υ,t) - мгновенное значение давления, P_max(υ) - максимальное давление, P_min(υ) – минимальное давление, DP(υ) - пульсовое давление при частоте сердцебиений υ.

Установлено [311], что форма пульсаций кровотока в крупных коронарных артериях совершенно аналогична. Отношение кровотоков в артериях в конце фазы напряжения (длина мышечных волокон постоянна) и в конце фазы сокращения (максимальное укорочение мышечных волокон) имеют значения, близкие к золотому числу 1,618 [193]. (Заметим, что при этом длина мышечных волокон уменьшается в 1,272= ) раз! [327, 329]) Поскольку отношения между значениями коронарного кровотока в характерных точках систолы не меняются [320], то золотое отношение является инвариантом количественной организации систолы кровотоковой ССЦ при любом уровне нагрузки.

Итак, рассмотренные «цепочки» временных, объемных, механических и кровотоковых «противоположностей» неизменно связаны с пропорцией золотого сечения. Гармония их сопряжения в соответствии с принципом оптимального вхождения имеет энергооптимальную основу.

2.3. «Золотые» соотношения между правым и левым желудочками

Отметим особенности соотношений между объемами стенки правого желудочка, межжелудочковой перегородки и стенки левого желудочка. Установлено [78], что объем стенки правого желудочка в 1,5 раз меньше объема межжелудочковой перегородки; объем межжелудочковой перегородки и объем стенки левого желудочка соотносятся аналогичным образом. Эти соотношения имеют место для различных видов млекопитающих. Особенность этих соотношений станет ясной, если рассмотреть их связь в виде двойного соотношения. Если некоторый целый объект d разделить на 3 части a, b и c, то их двойное соотношение W можно представить следующим образом: W = (a+b)(b+c)/bd; в нашем случае a=1, b=1,5, c=2,25, d=3,75. Соответственно, W= 9,375/7,125=1,315; эта величина всего на 0,5% отличается от золотого вурфа W=1,309. Отметим, что для трехзвенного членения тела, рук, ног и пальцев человека и млекопитающих величина W с небольшими отклонениями также близка к «золотому» значению [118]. По-видимому, Природа выбрала такие «рабочие» значения в диапазонах возможных величин a, b и с, при которых имеет место энергооптимальное соотношение объемов стенок правого и левого желудочков и межжелудочковой перегородки. Это предположение подтверждается тем, что при нормальных физиологических условиях КПД обоих сердец одинаков и равен максимально возможной величине 18-20% [240].

Установлено [241, 264], что отношение средних кровотоков в одинаковых объемах ткани левого и правого желудочков близко к золотому сечению (отклонение составляет 3-4%). Аналогичное соотношение для желудочков имеет место и по среднему потреблению кислорода одинаковыми объемами левого и правого желудочков [351]. В покое соотношение кровотоков в единичных объемах желудочков можно представить «золотым» соотношением:

/ @1,618,

где , – соответственно средний за сердечный цикл кровоток в единичном объеме левого и правого желудочков в золотом режиме кровоснабжения организма.

Соответственно, соотношение, включающее в себя потребление кислорода единичными объемами желудочков, также имеет «золотой» вид:

/ @ 1,618,

где , – соответственно среднее за сердечный цикл потребление кислорода в единичном объеме левого и правого желудочков в золотом режиме кровоснабжения организма.

Средняя величина рО₂ и скорость отдачи кислорода во всех регионах сердца в течение кардиоцикла одинакова [264, 269]. Исходя из представленных выше феноменов, очевидно, что существует также «золотое» соотношение открытых капилляров между их средними количествами за кардиоцикл в левом и правом желудочках (см. раздел 4.5):

/ @ 1,618,

где , – соответственно среднее за кардиоцикл количество открытых капилляров в единичном объеме левого и правого желудочков в золотом режиме.

Поскольку при нагрузке относительные изменения среднего кровотока и кислородного обеспечения в единичных объемах обоих желудочков аналогичны, то

d/d @ 1,618, (2.36)

d/d @1,618. (2.37)

Очевидно, что и соотношение среднего количества открытых капилляров в единичных объемах желудочков в режимах кровоснабжения также подчиняется золотому сечению (см. раздел 4.5):

/ @ 1,618. (2.38)

Можно сказать, стенки левого и правого желудочков «построены» из «кирпичей», обеспечение которых кровью, кислородом и сетью капилляров соотносится по золотому сечению. Причем в соответствии с (2.36) – (2.38), золотое соотношение сохраняется на всех уровнях нагрузки.

Таким образом, при естественном «объемном» сопряжении стенок желудочков и межжелудочковой перегородки, а также и естественном соотношении удельного потребления крови и кислорода за единицу времени обоими желудочками, имеет место наиболее эффективное сопряжение деятельности обоих сердец. Это сопряжение, как мы могли убедиться, связано с «участием» золотого вурфа и золотого сечения. По-видимому, аналогичные соотношения существуют и для стенок предсердий и их перегородки.

2.4. Биофизические основы энергооптимальной гармонии сердца

Раньше мы уже отмечали распространенность спирали в природе. Принцип спиралевидного движения можно наблюдать на микро- и макроуровнях живой и неживой природы, он является принципом наиболее эффективного и экономичного действия. Сердце образуется одной мышцей, для увеличения силы сокращения закрученной в золотую спираль с углом 22 – 25^оС [83]. Закрученные слои ткани петлями опоясывают отделы сердца. Спираль увеличивает частоту витков в области верхушки сердца, тем самым создавая максимальный градиент силы сокращения сердца. Особенность этой спирали заключается в том, что размер ее витков постепенно увеличивается, но их форма остается неизменной. Максимальная сила сокращения создается в области верхушки сердца, минимальная – в области предсердий и основания сердца. Скручивание сердечной мышцы по спирали обеспечивает большую силу при изгнании крови из желудочков, чем в случае простого линейного сокращения. Таким образом, создание необходимого градиента силы сокращения при спиральной конструкции мышцы обеспечивается при минимальной массе последней. Отметим еще одну особенность строения мышечной массы сердца. Мускулатура левого желудочка состоит из трех слоев - двух косых наружных и одного внутреннего циркуляторного (поперечного). Угол начального наклона «косых» волокон по отношению поперечным составляет 52,4^о [314]. Этот угол близок к углу 51,9^о в «золотом» прямоугольном треугольнике. «Золотой» треугольник с углами при гипотенузе 38,1 и 51,9^о обладает замечательным свойством: его стороны соотносятся между собою по геометрической прогрессии – 1, 1,272, 1,618 (или 1,618⁰, , 1,618). Свойства этого треугольника использовались еще в Древнем Египте при строительстве пирамиды Хеопса [30]. Отметим, что разница отношений катета к гипотенузе для треугольников с углами 52,4 и 51,9^о не превышает 1%. Проекции «косой» силы F по взаимно перпендикулярным осям левого желудочка приблизительно соответствуют «золотому» треугольнику: F_Г=0,611F, F_В=0,792F, где F_Г, F_В - проекции силы F на горизонтальную и вертикальную оси желудочка. Силы F_Г и F_В закручивают струю крови в желудочках, придавая ей вращательно-поступательное движение. Саллин [311], принимая форму левого желудочка близкой к эллипсоиду вращения, показал с учетом угла 52,4°, что ударный выброс крови при этих условиях составляет 36% от конечнодиастолического объема. Величина 36% близка к «золотой» - 38%, которая, как было представлено в 2.1.4, соответствует энергооптимальной величине ударного объема в покое. При конфигурации мышечной массы сердца выброс ударного объема крови происходит при минимальном потреблении кислорода [334].

Отметим, ламинарно- винтовое движение крови в желудочках представляет широко распространенную форму движения воздуха, жидкостей и крови в живых организмах. Кровь при поступательном движении вперед дополнительно вращается. Такой тип движения жидкости происходит с минимальной потерей энергии [43]. Очевидно, что «золотой» угол 52,4° является тем оптимальным углом, при котором имеет место гармония «противоположностей» - горизонтальной и вертикальной сил, обеспечивающая наиболее эффективное закручивание струи крови по спирали. Кроме того, и внутренняя поверхность левого желудочка (сосочковые мышцы и трабекулярный аппарат) образует спиральную структуру [177], по которой происходит движение крови по направлению к аортальному клапану. Вследствие этого, выброс адекватного количества крови происходит с минимальными затратами энергии на трение о стенку желудочков. Добавим к этому, спирализация внутренней поверхности желудочков имеет следствием спирализацию струи крови в течение периода изгнания, что обеспечивает максимальную скорость движения и минимальное время выброса единичного объема крови. Конструкция аорты геометрически подобна каналам, в которых движение жидкости происходит с минимальными потерями энергии [130]. Таким образом, взаимное «золотое» расположение мышечных пучков, золотая спиральность конструкции мышечной массы и в стенке желудочка и оптимальная конструкция аорты обеспечивают, в конечном счете, золотую гармонию «противоположностей» в структуре энергооптимального изгнания крови. Благодаря структурным особенностям сердечного комплекса обеспечивается значительная экономия мышечной массы.

(Необходимо указать на особую роль спирали в конструкции многих других биологических объектов. Спиралеобразность наблюдается во многих явлениях живой природы: паук плетет свою паутину спиралеобразно, испуганное стадо оленей разбегается по спирали, двойной спиралью закручена молекула ДНК, спирален рост корней и побегов, движение протоплазмы в клетках происходит по спирали и т. д. Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишек и рыб расположены по логарифмическим спиралям, закрученных навстречу друг другу. Добавим к этому, великий Гёте считал спиральность одним из характерных признаков всех живых организмов, самой сокровенной сущностью жизни, называя спираль «кривой жизни».)

Рассмотрим другие биофизические аспекты экономии. Майром с соавт. [293] было установлено, что в нормальных, естественных условиях правый и левый желудочки работают в оптимальном режиме, т.е. при максимальном выделении мощности на нагрузке (артериальная система). Показано [278], что максимальная энергия выделяется на нагрузке в том случае, когда внутреннее сопротивление насоса (сердца) и сопротивление нагрузки (артериальная система) равны; это соотношение реализовано в сердечно-сосудистой системе. Максимальному выделению мощности на нагрузке способствует и то обстоятельство, что коэффициенты растяжимости стенок левого желудочка и аорты одинаковы [287, 335]. За счет представленных аспектов экономии имеет место энергооптимальная гармония между «противоположностями» - производством механической энергии сердцем и ее потреблением на нагрузке (сосудистой системе). Таким образом, оптимальное сопряжение конструкции сердца с нагрузкой за счет перечисленных факторов позволяет сэкономить дополнительное количество потребляемой энергии и мышечного материала.

Дополнительно следует обратить внимание на некоторые другие конструктивные особенности сердца млекопитающих. Сердце включает в себя кроме мышечных волокон элементы, непосредственно не производящие механической работы (сосуды с кровью, проводящая и нервная системы, клапаны и т.д.). Объем миокарда по отношению к общему объему сердечных элементов составляет 37% (ЗС!) [200]. Таким образом, имеет место золотая гармония «противоположностей»: соотношение объемов мышечной и «вспомогательных» тканей. Поскольку установлено практически линейное сотношение между весом сердца и количеством мышечных волокон у различных животных независимо от их размеров [307], то золотой феномен имеет место у различных видов млекопитающих. Отметим, аналогичное соотношение имеет место и в кардиомиоцитах, где отношение объема энергопроизводящей части (митохондрии) к общему объему клетки составляет 34% [304]; При таком соотношении вхождение энергопроизводящих и энергопотребляющих субклеточных структур в систему «Кардиомиоцит» позволяет последнему исполнять свою функцию с минимальными затратами энергии и живого вещества. Показано [26], что на реализацию энергетических потребностей организма животных также используется «золотая доля» его массы (38%). Этот показатель сохраняется для различных представителей животного мира, включая и человека. Таким образом, золотое соотношение энергопроизводящей части к остальным является характерным признаком живых систем на уровне клетки, органа и организма в целом.

Интересно отметить также следующее обстоятельство. Установлено [78], что у различных видов млекопитающих вес стенки левого желудочка и вес межжелудочковой перегородки соотносятся между собою как числа Фибоначчи (3:2). Аналогичное соотношение существует также между межжелудочковой перегородкой и стенкой правого желудочка. Можно утверждать с большой степенью вероятности, что и для «верхней» части сердца (предсердий) существует аналогичное, «фибоначчиево» соотношение между весами стенок левого и правого предсердий и их перегородок. По-видимому, соотношение весов по числам Фибоначчи обеспечивает оптимальное сопряжение мышечной массы левого и правого сердец. В целом такое сопряжение является, по-видимому, еще одним аспектом экономии энергии и мышечного вещества.

Итак, налицо совокупность оптимальных «противоположностей» в мышечных слоях, в сердечных тканях, камерах сердца, системе «желудочек-нагрузка». Эта цепочка «противоположностей» является своего рода иллюстрацией к представленному нами принципу оптимального вхождения. Мы могли убедиться, что природа экономит энергию и живое вещество на всех уровнях систем сердца. Нельзя не вспомнить при этом, что еще Аристотель говорил: «Природа не делает при помощи большего, если это же можно сделать при помощи меньшего»!

2.5. «Цена» изгнания единичного объема крови

Установлено [113], что «подбор» нормального сердечного выброса за минуту и среднее артериальное давление являются оптимальным «решением» по отношению к системе эритропоэза. Покажем, что золотой режим кровоснабжения организма является для сердца самым экономичным по отношению к затратам механической мощности на изгнание единичного объема крови. Механическая работа сердца приходится на фазу изгнания крови из желудочков. Ударная работа A(υ_ЗС), производимая сердцем в течение фазы изгнания в золотом режиме,

A(υ_ЗС) = [1/t*_S(υ_ЗС)]p*(υ_ЗС,t)q*(υ_ЗС,t)dt, (2.39)

где t*_S(υ_ЗС) - длительность фазы изгнания, q*(υ_ЗС,t), p*(υ_ЗС,t), - мгновенные значения объемной скорости изгнания крови и давления в левом желудочке во время фазы изгнания при золотой частоте υ_ЗС.

Для левого желудочка в некотором режиме кровоснабжения при физической нагрузке по отношению к золотому режиму длительность изгнания [193]:

t*_S(υ) = t*_S(υ_ЗС)/. (2.40)

Давление p*(υ,t) и кровоток p*(υ,t), соответствующие частотам υ_ЗС и n [193],

p*(υ,t) = p*(υ_ЗС,t), (2.41)

q*(υ,t)= q*(υ_ЗС,t). (2.42)

Исходя из (2.40) – (2.42),

A(υ) = A(υ_ЗС), (2.43)

где A(υ) - ударная работа сердца в заданном режиме кровоснабжения при частоте сердцебиений υ.

Величина объема крови, выброшенного желудочком за одно сокращение при частотах υ и υ_ЗС,

V(υ_ЗС) = q*(υ_ЗС,t)dt,

V(υ) = q*(υ_ЗС,t)dt = V(υ_ЗС), (2.44)

где V(υ_ЗС), V(υ) - соответственно ударный объем крови в золотом и заданном режимах кровоснабжения организма; из (2.44) очевидно их равенство. Эффективность работы сердца по отношению к его функции определяется количеством механической энергии, затраченной на изгнание единичного объема крови. Исходя из (2.43) и (2.44),

h(υ) = А(υ)/V(υ) = h(υ_ЗС), (2.45)

где h(υ_ЗС), h(υ) - соответственно «цена» изгнания единичного объема крови в золотом и заданном режимах кровоснабжения. Заменив υ/υ_ЗС на d, можно (2.45) представить в следующем виде:

h(υ) = h(υ_ЗС).

Итак, «цена» изгнания крови в золотом режиме минимальна, а при наибольшей нагрузке максимальна. Отметим, что для всего организма наиболее экономный, золотой, режим кровоснабжения соответствует физиологическому покою организма. Этим объясняется возвращение кровообращения в исходный режим покоя после прекращения нагрузки.

2.6. Гемоартериальная система сердца и гармония ССЦ

2.6.1. Особенности конструкции и гемодинамики гемоартериальной

системы сердца в покое

Артерии, питающие ткани сердца, окружают сердце наподобие венца и поэтому называются коронарными или венечными. Первые две коронарные артерии (левая и правая), ответвляющиеся от начала восходящей части аорты, являются самыми крупными магистральными кровеносными сосудами. Эти сосуды расположены на эпикардиальной поверхности сердца. Пронизывая толщу миокарда, они последовательно делятся, уменьшаясь в диаметре. Докапиллярное сосудистое русло сердца по отношению к «кислородной» функции можно условно разделить на два участка: транспортный и обменный. По транспортному участку кровь перемещается без отдачи кислорода, на обменном отдает кислород. Транспортный участок составляют артерии с диаметром выше 100 мкм. К обменному участку относятся артериолы и метартериолы с диаметром менее 100 мкм.

Обеспечение сердца кровью и кислородом представляет собою замкнутый цикл: 1) сокращение сердца обеспечивает транспорт крови и кислорода в сердечной мышце и 2) утилизация кислорода и других веществ в кардиомиоцитах обеспечивает очередное сокращение сердца. Основу деятельности системы крово-кислородного обеспечения сердца составляет взаимодействие трех «партнеров»: взаимодействие трех «партнеров»: 1) переносчика кислорода – крови, 2) транспортного тракта - сосудистого русла и 3) движущего фактора - давления в аорте. С первыми двумя «партнерами» связаны структурные аспекты системы, с третьим - динамические. Среднее давление в аорте рефлекторно задает уровень кровотока в коронарных сосудах, а также уровень потребления кислорода сердечными клетками.

2.6.2. Гемодинамика сердечной мышцы в условиях гипертензии

Повышение артериального давления как следствие внешних «возмущающих» факторов, в том числе и физической нагрузки, принято называть гипертензией. Переходный период между сердечным выбросом в покое и стабильной величиной при градуированной нагрузке составляет порядка 5-7 минут. Установлено [175], что кратчайший поиск оптимальной величины стабильного параметра за переходный период происходит по числам Фибоначчи.

Связь между гипертензией и кровоснабжением организма млекопитающих в условиях физической нагрузки представлена отношением [193]:

/= = ,

где n_ЗС, n - соответственно частоты кровоснабжения организма и при некотором уровнесердцебиений в золотом режиме физической нагрузки; Q(n_ЗС), Q(n), ,- - соответственно минутный выброс сердца и среднее давление в аорте в золотом режиме кровоснабжения и при нагрузке; δ – уровень относительного изменения кровоснабжения организма и сердца при нагрузке. Уровень кровоснабжения сердца связан с величиной среднего давления в аорте. В дальнейшем для удобства анализа будем использовать отношение, связанное с изменением давления в аорте [193],

b = =/.

В качестве исходного режима гипертензии примем «золотой» режим гипертензии, функционально соответствующий «золотому» режиму кровоснабжения всего организма (b=b_ЗС=1). Значение b представляет относительный уровень изменения гипертензии по отношению к золотому режиму. В естественных пределах вариации физической нагрузки b=1¸2.

В качестве одной из особенностей гемодинамики сердца следует учесть важное обстоятельство. При изменении градуированной нагрузки имеют место аналогичные относительные изменения среднего кровотока в крупных и средних коронарных артериях независимо от их калибра [280, 347]. Из этого феномена следует: между кровотоками в крупных и средних артериях независимо от уровня физической нагрузки сохраняются соотношения, соответствующие покою. Также неизменно соотношение кровотоков в эндо- и эпикардиальных слоях миокарда в покое и при любой мышечной нагрузке [229]. Установлена неизменность отношения кровотока коронарном синусе к кровотоку в левой коронарной артерии при изменении давления в аорте и сжатии легочной артерии [309]. Показано [203], что представленные явления возможны лишь в том случае, если при нагрузке в каждом крупном, среднем и мелком артериальном сосуде средние за кардиоцикл, систолу и диастолу значения кровотока изменяются в одинаковой степени. Во всех крупных, средних и мелких коронарных артериях имеют место пульсации давления и кровотока, которые постепенно сглаживаются, а на границе микрососудов практически исчезают. Необходимо отметить, что форма пульсаций кровотока в коронарных артериях аналогична [311, 347] . Показано также [320], что соотношения между значениями коронарного кровотока в характерных точках кардиоцикла не меняются при любом уровне нагрузки. Добавим к этому, что относительное изменение давления на каждом сосуде в условиях гипертензии аналогично относительному изменению среднего давления в аорте [248]. Отмеченные феномены позволяют нам считать, что в коронарных артериях исходная форма кровотока и давления в течение кардиоцикла сохраняется во всех режимах гипертензии. Пульсации давления и кровотока по мере уменьшения диаметра постепенно сглаживаются (приближаются к прямой линии). На микроучастке пульсации давления и кровотока либо слабо выражены, либо вообще отсутствуют. Следовательно, в покое во всех коронарных артериях соотношение между систолической и диастолической составляющими, отнесенными к длительности кардиоцикла, и средней величиной за кардиоцикл для давления и кровотока соответствует золотой пропорции, т.е. имеет место золотая гармония «противоположностей». Отмеченные особенности позволяет нам сделать вывод: золотая гармония «противоположностей» имеет место также и для других гемодинамических параметров микрососудов (давление, проводимость, объем). Это обстоятельство упрощает нашу задачу, поскольку можно не производить анализ параметров отдельно для систолы, диастолы и сердечного цикла. В дальнейшем при рассмотрении изменений какого-либо параметра в сосуде в условиях гипертензии мы будем использовать его среднее за сердечный цикл значение. Для краткости будем обозначать эту величину «средним значением» параметра.

2.6.3. Условия оптимального движения крови в отдельном сердечном сосуде

В любом сосуде расход энергии, связанный с движущейся кровью, разделяется на следующие составляющие [113]: 1) расход энергии, теряемой в результате движения крови; 2) расход энергии, потребляемой в связи с генерацией клеточных элементов крови взамен погибающих; 3) расход энергии на метаболизм клеточных элементов крови. Затраты энергии, представленные в 1), 2) и 3), составляют «стоимость» дальнейшем будем обозначать мощность, расходуемую на перфузию сосуда, «механической», мощность, расходуемую на воспроизводство эритроцитов и метаболизм элементов крови, «химической». «Стоимость» затрат этих мощностей в сосуде с изменением диаметра сосуда изменяется в противоположных направлениях: при заданном кровотоке в сосуде с увеличением диаметра расход «механической» энергии падает, а «химической», наоборот, возрастает. Очевидно, что при некотором диаметре суммарный расход этих мощностей минимален. В соответствии с принципом «минимальности работы», выдвинутым Мюрреем [295], заданный кровоток в сердечном сосуде Q связан с его диаметром d и параметрами крови оптимальным соотношением:

Q/d³= (p/32), (2.46)

где x - вязкость крови, b - расход «химической» энергии в единичном объеме крови за единицу времени. Отметим, что в сердечных сосудах кровоток движется в соответствии с принципом минимальной работы [216, 193].

Механическую мощность W_M(b_ЗС) в золотом режиме гипертензии можно представить следующим выражением:

W_M(b_ЗС) = 128Q²(b_ЗС)x(b_ЗС)l(b_ЗС)/pd(b_ЗС)⁴,

Q(b_ЗС), d(b_ЗС), l(b_ЗС), x(b_ЗС) – соответственно кровоток в сосуде, диаметр и длина сосуда, вязкость крови в сосуде в золотом режиме гипертензии.

Химическую мощность в сосуде W_Х(b_ЗС) можно определить из выражения:

W_Х(b_ЗС)=b(b_ЗС)V(b_ЗС),

где V(b_ЗС), b(b_ЗС) – соответственно объем сосуда и расход химической энергии в единичном объеме сосуда за единицу времени в золотом режиме гипертензии.

Исходя из (2.44),

b(b_ЗС)=64x(b_ЗС)[l(b_ЗС)/d(b_ЗС)]².

Отметим, что величина химической мощности связана с диаметром d сосуда и реологически, поскольку вязкость крови b зависит от диаметра сосуда [242]. Показателем минимальных затрат энергии в сердечном сосуде с движущейся кровью в покое и режимах гипертензии является оптимальное отношение механической и химической мощностей [203]:

g(b) = W_M(b)/W_X(b)=W_M(b_ЗС)/W_Х(b_ЗС) = 0,5.

Отметим, что отношение W_M(b)/W_X(b) соответствует отношению чисел Фибоначчи (1:2). Величина g(b)=0,5 является инвариантом и представляет энергооптимальное соотношение энергетических «противоположностей» в каждом сердечном сосуде в покое и во всех режимах гипертензии [203].

2.6.4. Изменение гемодинамических параметров коронарного русла в режимах гипертензии

С кровью по коронарному руслу переносятся все необходимые для жизнедеятельности сердца вещества (глюкоза, аминокислоты, жирные кислоты, соли, вода и т.д.). Однако количество крови, протекающее через миокард, обусловлено, в первую очередь, его потребностью в кислороде. Обмен между кровью и тканями начинается на уровне артериол, которые, делясь, в дальнейшем образуют густую сеть капилляров, проходящих по преимуществу параллельно мышечным волокнам. По отношению к «кислородной» функции докапиллярное русло условно можно разделить на два участка: «транспортный» и «обменный». Транспортный участок включает в себя артерии эластического типа с диаметром свыше 500мкм и мышечные артерии с диаметром свыше 100 мкм. Через этот участок кровь движется без диффузии кислорода в окружающие ткани. Кислород начинает поступать в сердечные клетки на обменном участке, где микрососуды имеют диаметр менее 100 мкм [68, 247].

Увеличение физической нагрузки вызывает рост среднего давления в аорте, общего кровотока, общего объема и общей проводимости коронарного русла. Изменение двух последних параметров на участке эластических и мышечных артерий, составляющих транспортный участок, происходит за счет увеличения диаметра и длины сосудов. На уровне обменных микрососудов изменение суммарного объема и проводимости происходит за счет подключения дополнительного количества функционирующих сосудов, размеры которых практически постоянны. Добавим к этому, в крупных, средних и мелких коронарных сосудах пульсация кровотоков в течение кардиоцикла сопряжена с пульсациями стенки этих сосудов. По мере перемещения крови к сердечным артериям малого диаметра пульсации стенки, давления и кровотока все более сглаживаются. В мышечных артериях пульсации этих параметров незначительны, а на уровне микрососудов практически отсутствуют [341]. Таким образом, на домикрососудистых сосудах i-животного в условиях нагрузки устанавливаются следующие значения параметров [203]:

P(b,W_i) = bP(b_i_ЗС,W_i), (2.47)

Q(b,W_i)= b²Q(b_i_ЗС,W_i), (2.48)

V(b,W_i)=bV(b_i_ЗС,W_i), (2.49)

G(b_i_ЗС,W_i)=bG(b_i_ЗС,W_i), (2.50)

t(b_i_ЗС,W_i)= t(b_i_ЗС,W_i)/b, (2.51)

где Q(b_i_ЗС,W_i), Q(b,W_i)), V(b_i_ЗС,W_i), V(b,W_i), G(b_i_ЗС,W_i), G(b,W_i), t(b_i_ЗС,W_i), t(b,W_i)– соответственно общий средний коронарный кровоток, средний общий объем и средняя общая проводимость сердечного русла, время нахождения эритроцитов в сердечном русле i-животного в золотом и других режимах гипертензии.

Установлено [248], что при увеличении артериального давления в b раз давление DP(b_ЗС), приложенное к каждому артериальному сосуду в покое, возрастает аналогичным образом,

DP(b)=bDP(b_ЗС). (2.52)

Следует отметить, при любой гипертензии вязкость крови в каждой эластической и мышечной артерии изменяется незначительно, а в обменных сосудах и в капиллярах остается постоянной (см. рис. 3.6):

ξ(b)=ξ(b_ЗС), (2.53)

где ξ(b_ЗС), ξ(b) – вязкость крови в золотом и других режимах гипертензии.

Эластические и мышечные артерии при переходе от покоя к гипертензии расширяются и удлиняются. На эластических и мышечных артериях показано [346, 203], что при увеличении приложенного исходного давления P₀ до некоторой величины P их диаметр d₀ и длина l₀ изменяются в одинаковой степени:

d/d₀= l/l₀ = (DP/DP₀)^1/3.

С учетом (2.52) и (2.54), в условиях гипертензии размеры транспортных сосудов изменяются аналогичным образом:

d_m(b_i_,W_i)=b^1/3d_m(b_i_ЗС_,W_i), (2.54)

l_m(b_i_,W_i)=b^1/3l_m(b_i_ЗС_,W_i), (2.55)

где d_m(b_i_ЗС,W_i), d_m(b_i_,W_i), l_m(b_i_ЗС,W_i), l_m(b_i_,W_i) – соответственно диаметр и длина m-сосуда i-животного в золотом и других режимах гипертензии.

Исходя из (2.52) -(2.55), можно показать, что при гипертензии в каждом эластическом и мышечном сосуде транспортного участка имеет место оптимальное соотношение «противоположных» мощностей:

g(b) = W_M(b)/W_X(b)=W_м(b_ЗС)/W_Х(b_ЗС) = 0,5. (2.56)

В дальнейшем нами будет показано, что соотношение (2.56) имеет место и для микрососудов на обменном участке.

2.6.5. Гармония «противоположностей» докапиллярного русла

в золотом режиме гипертензии

Рассмотрим сопряжение «противоположностей» транспортного и обменного участков докапиллярного русла сердца млекопитающих.

«Противоположности» этих участка гемососудистого русла обусловлены прежде всего особенностями ветвления сердечных сосудов. На всем протяжении этого русла каждый сосуд разветвляется на две ветви; при этом образуется так называемый «тройник». На транспортном участке (d>100 мкм) сосуды эластического и мышечного типа разделяются на две несимметричных ветви. На «обменном» участке (7<d<100 мкм) сосуды, напротив, разветвляются на две приблизительно симметричные ветви [49]. Каждый тройник состоит из ствола с диаметром d_С и длиной l_С и двух ветвей с диаметрами d₁, d₂ и длинами l₁, l₂. Особенности архитектоники тройников в золотом режиме гипертензии (покое) можно представить тремя коэффициентами [216]:

1) коэффициент ветвления k(b_ЗС)

k(b_ЗС) = [d₁(b_ЗС)² + d₂(b_ЗС)²]/d_С(b_ЗС)²,

2) коэффициенты относительного сечения ветвей H₁(b_ЗС) и H₂(b_ЗС)

H₁(b_ЗС) = d₁(b_ЗС)²/[d₁(b_ЗС)² + d₂(b_ЗС)²],

H₂(b_ЗС) = d₂(b_ЗС)²/[d₁(b_ЗС)² + d₂(b_ЗС)²],

Из этих соотношений следует [193]:

d₁(b_ЗС) = d_С(b_ЗС), (2.57))

d₂(b_ЗС) = d_С(b_ЗС). (2.58)

Установлено [216], что для сердечных сосудов величина k(b_ЗС) находится в пределах энергооптимального диапазона 1<k(b_ЗС)£1,26 («режим минимальной работы»). В этих пределах энергооптимальному сопряжению диаметров ствола и ветвей соответствует соотношение «кубов» [131]:

d₁(b_ЗС)³+ d₂(b_ЗС)³= d_С(b_ЗС)³. (2.59)

Соотношение (2.59) означает, что суммарный расход энергии, потраченной в каждом сосуде тройника на движение и биохимические процессы в крови, равен минимальной величине.

Отметим важное обстоятельство: эластические и мышечные тройники асимметричны (диаметры и длины ветвей неодинаковы). В этом феномене состоит важная особенность конструкции всего транспортного участка. Асимметрия тройников связана с тем, что удельное потребление кислорода в отдельных регионах сердца неодинаково (левый и правый желудочки, эндокард и эпикард и т. д.). Поэтому в различных областях сердечной мышцы плотность сосудистой сети неодинакова и соответствует уровню потребления кислорода. Этим обстоятельством и объясняется асимметричность эластических и

рис

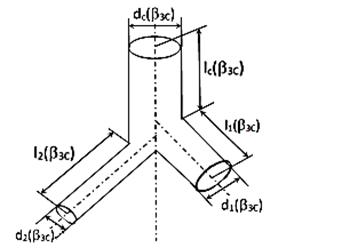
Рис. 2.5. Сосудистый тройник.

d_с(b_ЗС), d₁(b_ЗС), d₂(b_ЗС), l_с(b_ЗС), l₁(b_ЗС), l₂(b_ЗС)- соответственно диаметр и длина ствола,1 и 2 ветвей в золотом режиме гипертензии

мышечных тройников: одна из ветвей имеет больший диаметр, чем вторая. кроме того, толстая ветвь с большим диаметром имеет меньшую длину, чем тонкая (см. рис. 2.5). Следует заметить, чем ближе разветвления к аорте, тем больше их асимметрия. С другой стороны, разветвления приобретают все менее выраженную асимметрию по мере приближения к микрососудам. Длины ветвей и ствола тройника не связаны между собою выражениями типа (2.57)–(2.59). Неравенство длин имеет большое «кислородное» значение. Для адекватного кислородного обеспечения сердечной мышцы каждый из эритроцитов, одновременно поступивших из аорты в исходное сечение первой коронарной артерии, должен достигнуть «своего» первого обменного микрососуда в один и тот же момент времени. В противном случае, если синхронизация вхождения будет нарушена, исходная порция эритроцитов будет «расплываться». Выравнивание по времени происходит следующим образом. Естественно, первая, «толстая», ветвь первого асимметричного эластического тройника при дальнейшем ветвлении до микрососуда с d(b_ЗС) » 100 мкм в соответствии с (2.57), имеет большее число ветвлений, чем вторая, «тонкая» (2.58). Для того чтобы обеспечить, в конечном счете, одинаковое давление на входе всех микрососудов падение давления на «тонкой» ветви каждого домикрососудистого тройника должно быть больше, чем на «толстой» ветви. Этого состояния при сохранении величины кровотока через тонкий сосуд можно достигнуть только за счет удлинения «тонкой» ветви по сравнению с «толстой». Легко показать, что при этом время нахождения эритроцитов в «тонких» ветвях возрастает в той же степени, что и давление. Таким образом, «подбор» длины «толстых» и «тонких» ветвей в тройниках позволяет обеспечить в итоге не только одинаковое давление на входе микрососудов, но также и одинаковое время пребывания в пути всех эритроцитов исходного объема. В дальнейшем в симметричных ветвях обменных тройников (l₁(b_ЗС)=l₂(b_ЗС)) происходит синхронное движение «исходных» эритроцитов. На всех микрососудах создается одинаковая разность давлений [203]. При этом обеспечивается одинаковое время пребывания эритроцитов во всех сосудов данной генерации. Аналогия давлений и времени пребывания эритроцитов в каждой генерации обменных сосудов обеспечивает одинаковое «качество» кислорода, поступающего в кардиомиоциты по всему объему сердечной мышцы (см. раздел 3.4.3). Добавим к этому, давление на артериальном конце капилляров не должно превышать критическую величину 35 мм рт. ст., выше которой начинается отек тканей.

В заключение можно сказать, «противоположные» типы ветвления (асимметрия и симметрия) в эластических, мышечных и обменных тройниках создают гибкую структуру, которая позволяет обеспечить энергооптимальный транспорт адекватного объема кислорода в различные по уровню потребления области сердца. «Асимметричный» и «симметричный» типы ветвления создают оптимальную гармонию «противоположностей», которая обеспечивает адекватное кислородное снабжение по «качеству» и «количеству» по всему объему миокарда.

2.7. Гармония «противоположностей» ССЦ на обменном участке артериального русла

2.7.1. Гемодинамические параметры микрососудистых тройников в режимах гипертензии

Установлено [49], что микрососудистые тройники приблизительно симметричны, т.е. d₁(b_ЗС)»d₂(b_ЗС), l₁(b_ЗС) »l₂(b_ЗС). С некоторой погрешностью для всех «обменных» тройников примем k(b_ЗС) = 1,26, H₁(b_ЗС) = H₂(b_ЗС)= 0,5. Рассмотрим соотношения диаметров и длин ствола для последовательных звеньев длинной цепочки тройников с привлечением коэффициентов k(b_ЗС) и H(b_ЗС). Для оценки взаимосвязи между длиной и диаметром сосуда введем параметр конструкции сосуда С(b_ЗС)=l(b_ЗС)/d(b_ЗС). Уникальность этого параметра состоит в том, что распределение величины этого параметра по цепочке коронарных микрососудов аналогично для млекопитающих, земноводных и рыб [216]. Были установлены, вплоть до капилляра, особенности изменения параметра конструкции по цепочке обменных микрососудов; по этой цепочке движется отдельный эритроцит. Для части цепочки, где d(b_ЗС)>40 мкм, С(b_ЗС)=3. На «обменной» части цепочки с d(b_ЗС)<40 мкм по мере сужения сосудов параметр С(b_ЗС) возрастает от 4 до 6. Отметим, при гипертензии размеры сосудов на микрососудистом участке практически не меняются. Жесткость стенок микрососудов является фактором, «гасящим» пульсации артериального давления и кровотока. Естественно, что микрососудистых тройниках во всех режимах гипертензии: для ствола C_С(b)=C_С(b_ЗС) и для первой и второй ветвей C₁(b)=C₁(b_ЗС), C₂(b)=C₂(b_ЗС). Представленная в книге К.А. Шошенко и др. [216] экспериментальная зависимость k=f(H) позволила установить, что для обменного участка коронарного русла в пределах d»10÷200 мкм величина k=1,10-1,20, что соответствует энергооптимальному режиму «минимальной работы». В пределах d=10÷40 мкм величина коэффициента k близка к полной симметрии ветвлений.

Установлено постоянство в течение сердечного цикла давления на микрососудах [92], а также размеров сердечных артериол и капилляров [227]. Исходя из постоянства в течение кардиоцикла диаметра и длины микрососудов, приложенного к ним давления и других, связанных с ними, параметров в дальнейшем будем использовать для анализа значения, средние за кардиоцикл.

Отдача кислорода на микрососудистом русле в основном происходит на участке 7<d<40мкм [203]. Важнейшую особенность этого участка сердца составляют обратно пропорциональные относительные изменения вязкости крови x и параметра конструкции С при переходе от ствола к ветвям [193, 203]:

x₁(b_ЗС)/x_С(b_ЗС) @ l_С(b_ЗС)/l₁(b_ЗС),

x₂(b_ЗС)/x_С(b_ЗС) @ l_С(b_ЗС)/l₂(b_ЗС).

На участке кривой вязкости крови x=f(d), соответствующем 7<d<100 мкм (см. рис. 3.6), вязкость крови в каждом сосуде: x₁(b)=x₁(b_ЗС), x₂(b=x₂(b_ЗС) и x_С(b)=x_С(b_ЗС), поскольку диаметры в этом диапазоне остаются неизменными при любой гипертензии. Остаются неизменными и длины сосудов. Следовательно, представленные выше соотношения и при гипертензии сохраняются неизменными. Между стволом и ветвями обменных тройников существуют обратно пропорциональные относительные изменения вязкости крови x(b_ЗС), длины (l(b_ЗС)) и времени пребывания эритоцитов t(b_ЗС) [193, 203]:

x₁(b_ЗС) = x₂(b_ЗС) = [С₁(b_ЗС)/С_С(b_ЗС)]x_С(b_ЗС),

l₁(b_ЗС) = l₂(b_ЗС) = 0,794[С_C(b_ЗС)/С₁(b_ЗС)]x_С(b_ЗС).

t₁(b_ЗС) = t₂(b_ЗС) = 0,794[С_C(b_ЗС)/С₁(b_ЗС)]x_С(b_ЗС).

(Отметим, что 1/0,794@=1,272, что указывает на «присутствие» в архитектонике обменных тройников золотого числа 1,618).

При гипертензии в обменных тройниках гемодинамические параметры изменяются следующим образом: [193, 194]:

ΔP₁(b) = ΔP₂(b) = bΔP_C(b_ЗС), (2.60)

q₁(b) = q₂(b) = 0,5bq_C(b_ЗС), (2.61)

d₁(b) = d₂(b) = 0,794d_C(b_ЗС), (2.62)

l₁(b) = l₂(b) = 0,794[C₁(b_ЗС)/C_C(b_ЗС)]l_C(b_ЗС), (2.63)

x₁(b) = x₂(b) = [C_C(b_ЗС)/C₁(b_ЗС)]x_C(b_ЗС), (2.64)

t₁(b) = t₂(b) = [C₁(b_С)/C_C(b_ЗС)]t_C(b_ЗС)/b, (2.65)

b₁(b) = b₂(b) = b_c(b) = b²b_c(b_ЗС), (2.66)

где ΔP₁(b),ΔP₂(b),ΔP_C(b), q₁(b), q₂(b), q_C(b), t₁(b), t₂(b), t_C(b), b₁(b), b₂(b), b_C(b) - соответственно приложенное к сосудам тройника давление, кровоток, время пребывания эритроцита, удельное потребление химической энергии за единицу времени в режиме гипертензии.

Исходя из (2.60) – (2.66), можно показать, что в каждом сосуде тройников имеет место оптимальное соотношение «противоположных» мощностей [203]:

g(b) = b²W_М1(b_ЗС)/b²W_Х1(b_ЗС) = b²W_М2(b_ЗС)/b²W_Х2(b_ЗС) =b²W_МС(b_ЗС)/b²W_ХС(b_ЗС) = 0,5.

где W_МС(b_ЗС), W_М1(b_ЗС), W_М2(b_ЗС), W_ХС(b_ЗС), W_Х1(b_ЗС), W_Х2(b_ЗС) – затраты механической и химической энергии за единицу времени в стволе и ветвях в золотом режиме гипертензии. Это отношение является энергооптимальным вариантом каждого из обменных тройников в покое и режимах гипертензии. Другим энергооптимальным показателем обменных тройников является выражение [216]:

[k(b)H₁(b)]^3/2+ [k(b)H₂(b)]^3/2 = 1. (2.67)

Это выражение характеризует энергооптимальную архитектонику тройников в режимах гипертензии.

Таким образом, в обменных тройниках оптимальное соотношение «противоположных» мощностей g(b)=0,5 остается неизменным для всякого микрососуда при любом уровне гипертезии. Оптимальное ветвление - [k(b)H₁(b)]^3/2+[k(b)H₂(b)]^3/2 =1 - имеет место для всех тройников при каждом уровне гипертензии. Если g(b)=0,5 отражает гармонию «противоположных» мощностей (механической и химической) в каждом сердечном сосуде, то [k(b)H₁(b)]^3/2+[k(b)H₂(b)]^3/2=1 представляет гармонию энергооптимального вхождения ствола и ветвей в единое сложное целое – тройник. Эти величины являются энергооптимальными критериями гармонии микрососудистых тройников в покое и при любом уровне нагрузки.

2.8. Микрососудистое «пространство» ССЦ и его особенности

Рассмотрим особенности прекапиллярных генераций микрососудов. Прежде всего, следует отметить, что архитектоника микроциркуляторного участка различных видов млекопитающих аналогична. На это обстоятельство указывают многие исследователи. В частности, Каро [76] обращает внимание на поразительное сходство размеров мелких сосудов млекопитающих, несмотря на значительное различие по массе тела. К.А.Шошенко отмечает аналогию отношений l/d для коронарных микрососудов не только для млекопитающих, но и рыб. Ветвления терминальных обменных артериол близки к симметричным (H₁»0,5, H₂»0,5, k»1,26) [49]. Необходимо указать на еще одну важную особенность: размеры терминальных сердечных артериол практически постоянны в течение сердечного цикла [341]. Установлено [68, 247], что кислород поступает в ткани не только из капилляров, но также и из микрососудов (прекапиллярных артериол и посткапиллярных венул).

Показано [203], что основной газообмен между кровью и тканями на микроучастке происходит на 8 прекапиллярных генерациях, начиная от капилляров (m=1, 2, …8). Рассмотрим в качестве «рабочей» системы цепочку из 8 обменных микрососудов, по которой отдельный эритроцит перемещается по направлению к капилляру. Исходя из (2.62), (2.63) и (2.65) и используя исходные значения этих параметров в первом сосуде (m=1), можно легко рассчитать величины этих параметров в остальных сосудах. Необходимые расчеты представлены нами в разделе 3.6 (см. Табл. 4).

В любом m-сосуде рассматриваемой нами цепочки, начиная от капилляра, величины ΔP_m(b_ЗС), d_m(b_ЗС), l_m(b_ЗС) и ξ_m(b_ЗС) постоянны в течение всего кардиоцикла. Естественно, что не меняются в течение сердечного цикла и другие параметры, рассчитанные с использованием этих величин - Q_m(b_ЗС), t_m(b_ЗС), V(b_ЗС) и G_m(b_ЗС). Величина скорости отдачи кислорода отдельным эритроцитом U_m(b_ЗС) и разности концентраций кислорода в крови m-сосуда также постоянны в течение сердечного цикла [194, 198]. Такая закономерность позволяет нам представленные выше параметры для удобства анализа обозначить общим символом А:

А_S_m(b_ЗС) = А_D_m(b_ЗС) = , (2.68)

где А_S_m(b_ЗС), А_D_m(b_ЗС), - соответственно средние значения рассматриваемых параметров в m-сосуде за систолу, диастолу и сердечный цикл в золотом режиме гипертензии.

Рассмотрим «вклад» систолической и диастолической составляющих в среднее за кардиоцикл значение некоторого j-параметра . Средние за сердечный цикл систолическое и диастолическое значения j-параметра в обобщенной форме можно представить в следующем виде:

= [t_S(b_ЗС)/T(b_ЗС)],

= [t_D(b_ЗС)/T(b_ЗС)],

где , - средние по отношению к длительности кардиоцикла систолические и диастолические величины j-параметра в m-сосуде, T(b_ЗС), t_S(b_ЗС), t_D(b_ЗС) - длительность систолы, диастолы и сердечного цикла в золотом режиме гипертензии. Вследствие того, что t_S(b_ЗС)/T(b_ЗС)=0,382 и t_D(b_ЗС)/T(b_ЗС)=0,618, выражение (2.68) преобразуется к виду:

0,382+ 0,618= . (2.69)

С учетом (2.68) и (2.69), закон композиции ССЦ для рассматриваемых гемодинамических и кислородных параметров на терминальном участке цепочки при гипертензии можно представить обобщенным выражением [200]:

0,382b+ 0,618b= b, (2.70)

где k_j - показатель степени, соответствующий j-параметру (эта величина постоянна и не зависит от «номера» сосуда). В законе (2.70) представлено микроциркуляторное «пространство» ССЦ рассматриваемых выше j-параметров. Очевидна «золотая» аналогия «противоположностей» в законах (2.70) и (2.28).

Вследствие полного сходства микроциркуляторного участка всех млекопитающих очевидна независимость величины любого j-параметра отдельного m-сосуда от веса животных. Величина j-параметра зависит только от порядкового номера сосуда m в цепочке микрососудов и величины гипертензии b. Для конкретизации закона (2.70) рассмотрим изменение параметров от первого звена до конечного по направлению к аорте. Это преобразование можно представить следующим образом [200]:

= , (2.71)

где С₁(b_ЗС), С_m(b_ЗС) - соответственно коэффициенты конструкции первого и m-сосуда в золотом режиме гипертензии; a_j и b_j постоянные коэффициенты, соответствующие j-параметру при- любой гипертензии. Поскольку при гипертензии диаметр и длина микрососудов не меняются, то С_m(b)/С₁(b)=С_m(b_ЗС)/С₁(b_ЗС), k_m(b)H_m(b)=k_m(b_ЗС)H_m(b_ЗС)=0,63. При любой гипертензии == = 0,794. (Отметим, что число 1/0,794=1,26 @ ).

Исходя из выражений (2.70) и (2.71), можно представить обобщенный закон композиции микроциркуляторного «пространства» ССЦ в следующем виде [200]:

0,382b[(C_m(b_ЗС)/С₁(b_ЗС)] +0,618b[(C_m(b_ЗС)/С₁(b_ЗС)] @ b((C_m(b_ЗС)/С₁(b_ЗС)). (2.72)

Нами были установлены [200] следующие постоянные величины для каждого m-параметра в (2.72). Величины k_j, a_j и b_j следующие: для давления (механическая ССЦ) k_j =1, a_j =0, b_j =0, для кровотока (кровотоковая ССЦ) - k_j =1, a_j =0, b_j=-3, для объема сосуда (объемная ССЦ) k_j =0, a_j =1, b_j = -3, для проводимости сосуда (проводимостная ССЦ) - k_j=0, a_j=0, b_j,=-3,для времени пребывания эритроцита (временная ССЦ) - k_j=-1, a_j=1, b_j =0, для скорости отдачи кислорода отдельным эритроцитом (диффузионная ССЦ) - k_j =0, a_j=0, b_j=2, для разности концентраций кислорода (разностная ССЦ) - k=-1, a_j =1, b_j =2. Величины a_j, b_j и k_j представлены в Табл. 2.

Представим конкретные значения параметров . Для m=1÷2 величина C_m(b_ЗС)=6, для m=3÷5 - C_m(b_ЗС)=5, для m=6÷8 - величина C_m(b_ЗС)=4, для m<8 - C_m(b_ЗС)=3. Величины для некоторых параметров представлены в разделе 3.6 (см. Табл. 4). Ниже рассчитаны значения следующих j-параметров [200]: давление =3,5 мм рт. ст., скорость отдачи кислорода отдельным эритроцитом в первом прекапиллярном сосуде сосуда=127,6%/с, разность концентраций кислорода в крови =5,49% и время пребывания с.

Табл. 2. Постоянные j-коэффициенты микроциркуляторного «пространства» ССЦ

j-ССЦ	j-коэффициенты
j-ССЦ	a_j	b_j	k_j
Механическая	0	0	1
Кровотоковая	0	-3	1
Объемная	1	-3	0
Проводимостная	0	-3	0
Временная	1	0	-1
Диффузионная	0	2	0
Разностная	1	2	-1

По известным значениям t₁(b_ЗС) =0,037 с, ΔP₁(b_ЗС) =3,5 мм рт. ст., ξ₁(b_ЗС) = 1,45×10^-2 Пз, d₁(b_ЗС)=6,9×10^-4 см и С₁(b_ЗС)=6 нами получены значения для других параметров первого звена цепочки: = 41,9×10^-9 см³с^-1, =1,53×10^-9 см³, =9,1×10^-11 г^-1см⁵с^-1. Используя эти величины и С₁(b_ЗС)=6 в качестве исходных, можно вычислить средние значения параметров для других звеньев обменной цепочки.

В обобщенном законе (2.72), как и в законе (2.28), можно отметить те же характерные математические особенности. В его структуре имеет место «пересечение» двух геометрических прогрессий: 1) Ф^-2 = 0,382, Ф^-1 = 0,618, Ф⁰ = 1 и 2) b^-1, b⁰, b. Первая прогрессия – «золотая» - представляет гармонию сердечных «противоположностей» при покое организма. Вторая в определенных пределах (b=1-2) связана с золотыми числами и в этих пределах обусловливает энергооптимальную гармонию «противоположностей» при гипертензии. Следовательно, в пределах допустимой гипертензии «противоположности» можно условно назвать «золотыми».

В (2.72) отображена уникальная роль золотого сечения в организации «противоположностей» этого «пространства», а также представлено влияние на ССЦ уровня гипертензии и порядкового номера звена цепочки. Числовой каркас (2.72) имеет иерархию, сходную с «пространством» (2.28). Прежде всего, каждому числу m соответствуют «свои» средние значения рассматриваемых параметров в золотом режиме гипертензии. При этом каждому j-параметру соответствуют свои постоянные величины a_j и b_j. Золотые числа 0,382 и 0,618 характеризуют гармонию «противоположностей» в средних значениях; они «присутствуют» в золотом режиме гипертензии (покое) в ССЦ всех рассматриваемых параметров в каждом из звеньев цепочки. При гипертензии оптимальные отклонения «от золота» каждого из j-параметров характеризуют «свои» числа k_j, k_j+1 и k_j-1. Диапазон гипертензии b=1-2 постоянен для любого параметра и номера сосуда. Представленные постоянные числа образуют оптимальный числовой «каркас» микроциркуляторного «пространства» ССЦ (см. Табл. 2).

Аналогия «пространств» (2.28) и (2.72) заключается в том, что в основе того и другого лежит энергооптимальное тождество (2.27). Основу «противоположностей» микроциркуляторного «пространства» (2.72), как и «пространства» (2.28), составляют отношения гармонии:

n_S(b) = 0,382b,

n_D(b) = 0,618/b,

где n_S(b), n_D(b) - соответственно отношение средних систолической и диастолической величин j-параметра, усредненных по отношению к кардиоциклу, к среднему за сердечный цикл значению этого параметра при различных уровнях гипертензии. Отношения n_S(b) и n_D(b) представляют основу «золотых противоположностей» для всего «пространства» ССЦ микрососудистого русла. Особенностью «пространства» (2.72) является равенство величины всякого j-параметра в «одноименном» m-сосуде всех животных независимо от их веса. По этой причине можно говорить о полном тождестве параметров обменных цепочек у различных видов млекопитающих.

2.9. Капиллярное «пространство» ССЦ

Несомненно, что для организации и структуры капиллярной сети сердечной мышцы определяющими является и гемодинамика, и газообмен. С этой точки зрения, каждый сердечный капилляр одновременно является звеном двух цепочек сосудов – «гемодинамической» и «диффузионной». Первая является цепочкой артериальных сосудов, включая капилляр, по которой отдельный эритроцит транспортирует кислород. Каждый капилляр является также звеном цепочки последовательно соединенных между собою капилляров, отдающих кислород и параллельных мышечному волокну. Таким образом, для каждого отдельного капилляра существует свое «пространство» ССЦ архитектонических, гемодинамических и кислородных параметров.

2.9.1 Законы изменения капиллярных параметров в режимах гипертензии

Структуре и гемодинамике отдельного капилляра и в покое, и при гипертензии присущи характерные признаки, общие для всего объема сердечной мышцы млекопитающих. К ним следует отнести:

1. Размеры капилляров одинаковы по всему объему сердца [339].

2. Независимо от степени механического сжатия диаметр, длина, площадь и конфигурация внутренней поверхности капилляров остаются неизменными [336].

3. Движение крови в капиллярах имеет ламинарный характер [119].

Гемодинамические параметры капилляров связаны определенными соотношениями с изменениями среднего аортального давления. На уровне микрососудов пульсация давления и кровотока незначительна, а в капиллярах практически отсутствует [76]. Практическое отсутствие пульсовых колебаний в капилляре обеспечивает неизменность его параметров в течение кардиоцикла. Поскольку средние значения этих параметров за систолу, диастолу и за сердечный цикл аналогичны, будем рассматривать только средние за кардиоцикл величины параметров.

При гипертензии размеры капилляров и вязкость крови в капиллярах не изменяются [203]:

d_K(b) = d_K(b_ЗС),

l_K(b) = l_K(b_ЗС),

x_K(b) = x_K(b_ЗС),

где d_K(b_ЗС), d_K(b), l_K(b_ЗС), l_K(b), x_K(b_ЗС), x_K(b) - соответственно диаметр, длина и вязкость крови в капилляре в золотом и других режимах гипертензии. Исходя из этих соотношений,

V_K(b) = V_K(b_ЗС), (2.73)

G_K(b) = G_K(b_ЗС), (2.74)

где V_K(b_ЗС), V_K(b), G_K(b_ЗС), G_K(b) - соответственно объем и проводимость капилляра в золотом и других режимах гипертензии.

Гемодинамические параметры капилляра в условиях гипертензии [203]:

ΔP_K(b) = bΔP_K(b_ЗС), (2.75)

q_K(b) = bq_K(b_ЗС), (2.76)

b_K(b) =b²b_K(b_ЗС), (2.77)

где ΔP_K(b_ЗС), ΔP_K(b), q_K(b_ЗС), q_K(b), b_K(b_ЗС), b_K(b) - соответственно давление, приложенное к капилляру, кровоток в нем, удельное потребление «химической» мощности, t_к(b_ЗС), t_к(b) - время пребывания эритроцитов в капилляре в золотом и других режимах гипертензии.

С учетом (2.73) – (2.77), можно показать, что в условиях гипертензии:

W_М_K(b) = b²W_М_K(b_ЗС),

W_Х_K(b) = b²W_Х_K(b_ЗС),

где W_М_K(b_ЗС), W_М_K(b), W_ХС(b_зс), W_Х_K(b) - соответственно механическая и химическая мощность, расходуемая в капилляре в золотом и других режимах гипертензии. Соответственно, отношение «противоположностей»: механической и химической мощностей в капилляре:

g_K(b) = g_K(b_ЗС) = 0,5.

Очевидно, что по аналогии с (2.67) в переходных тройниках (артериола - капилляры):

[k(b)H₁(b)]^3/2+ [k(b)H₂(b)]^3/2 = 1.

Оптимальное отношение «противоположностей» (g(b)=0,5) остается неизменным для любого капилляра при любом уровне гипертезии. Оптимальное ветвление ([k(b)H₁(b)]^3/2+[k(b)H₂(b)]^3/2 =1) аналогично для всех артериолярно-капиллярных тройников во всех режимах гипертензии. Если инвариант g(b)=0,5 отражает гармонию «противоположных» мощностей (механической и химической) в каждом сердечном капилляре, то инвариант [k(b)H₁(b)]^3/2+[k(b)H₂(b)]^3/2=1 представляет энергооптимальное вхождение ствола (артериолы) и ветвей (капилляров) в единое сложное целое – тройник.

2.9.2. Капиллярное «пространство» ССЦ и особенности его организации

Размеры, вязкость крови и давление в капилляре остаются постоянными в течение сердечного цикла. Следовательно, средние значения гемодинамических параметров открытого капилляра за систолу и диастолу равны друг другу: ΔP_S(b_ЗС)=ΔP_D(b_ЗС), q_S(b_ЗС)=q_D(b_ЗС), t_S(b_ЗС)=t_D(b_ЗС), V_S(b_ЗС)=V_D(b_ЗС) и G_S(b_ЗС)=G_D(b_ЗС). Показано [194], что в течение кардиоцикла скорость отдачи кислорода в капилляре, разность концентраций и напряжений кислорода в крови на концах капилляра также неизменны: U_S(b_С)=U_D(b_ЗС), ΔHbO₂_S(b_ЗС)=ΔHbO₂_D(b_ЗС) и ΔpO₂_S(b_ЗС)= ΔpO₂_D(b_ЗС). (Индексы S и D указывают на систолическую и диастолическую части капиллярного параметра.)

В обобщенном виде средние за сердечный цикл систолическое и диастолическое значения некоторого j-параметра, отнесенные к длительности сердечного цикла, в режиме гипертензии можно представить следующими выражениями:

= t_S(b)/T(b),

= t_D(b)/T(b),

где, , - соответственно средние за сердечный цикл систолическая и диастолическая величины и среднее за сердечный цикл значение j-параметра, t_S(b), t_D(b), T(b) - длительность систолы, диастолы и кардиоцикла в режиме гипертензии.

Поскольку в золотом режиме гипертензии длительности систолы, диастолы и кардиоцикла связаны между собою пропорцией золотого сечения, а величины всех рассматриваемых параметров неизменны в течение всего сердечного цикла, то законы их композиции можно представить в обобщенной форме:

= 0,382,

= 0,618,

0,382 + 0,618=,

где - средняя за сердечный цикл величина j-параметра в золотом режиме гипертензии.

Закон преобразования ССЦ капиллярных j-параметров в условиях гипертензии можно представить следующим обобщенным выражением [194]:

0,382b+ 0,618b@ b, (2.78)

где k_j- показатель, соответствующий j-параметру. Закон (2.78) представляет капиллярное «пространство» j-ССЦ. Отметим, что в (2.78) отсутствуют вес животного (см. (2.28)) и номер микрососуда (см. 2.72). В (2.78) гемодинамические и кислородные параметры капилляра при гипертензии имеют следующие значения [194]: для давления (механическая ССЦ) и кровотока (кровотоковая ССЦ) - k_j=1, для объема (объемная ССЦ), проводимости (проводимостная ССЦ), для скорости отдачи кислорода (диффузионная ССЦ), для разности напряжения кислорода (кислородная ССЦ) - k_j=0 и для разности концентраций кислорода в крови (разностная ССЦ) и для времени пребывания (временная ССЦ) - k_j=-1. Величины других капиллярных параметров: q_K(b_ЗС)=20,9×10^-9 см³с^-1, d_K(b_зс)=5,5 мкм, ξ_K(b_зс)=1,15×10^-2Пз, t_K(b_зс)=0,25 с и l_K(b_зс)=220 мкм. Средние за сердечный цикл величины имеют значения: =15,5 мм рт. ст., =4,8×10^-9 см³, =0,95×10^-11 г^-1см⁵с^-1. Соответственно, величины = 215%/c, = 55% и = 30 мм рт. ст.

В «пространстве» (2.76) по отношению к (2.28) и (2.70) продолжается «упрощение» структуры j-ССЦ: величины не зависят от веса животных и номера капилляра, а только от уровня гипертензии. В (2.76) так же, как и в (2.28) и (2.72), имеет место «пересечение» двух геометрических прогрессий: 1) «золотой»: Ф^-2 = 0,382, Ф^-1=0,618, Ф⁰ =1 и 2) х^-1 , х⁰ , х (см. разделы 2.1.3 и 2.8).

Элементы j-ССЦ в покое и при гипертензии, так или иначе, связаны с золотыми числами 0,382 и 0,618 в «чистом» виде и оптимальными отклонениями от них. Поэтому «пространство» (2.78) следует рассматривать как множество «золотых» гармоний в пределах от покоя до максимальной гипертензии (нагрузки). При всяком уровне относительной гипертензии b у всех животных независимо от их вида и веса отношение капиллярных j-«противоположностей» аналогично, что указывает на тождество «перехода» величины j-параметра от одного животного к другому. Следует отметить еще одно важное обстоятельство: у всей генерации капилляров значения j-параметра, соответствующие некоторому уровню гипертензии b, аналогичны. Таким образом, в пределах b=1÷2 происходит тождественное «тиражирование» оптимальных величин и «золотых противоположностей» параметров от одного капилляра к другому независимо от плотности капиллярной сети и веса животных. Можно говорить о тождестве «пространств» всех открытых капилляров.

Числовой каркас (2.78) имеет иерархию, сходную с «пространством» (2.8). Средние рабочие значения j-параметров определяются «подбором» оптимальных «противоположностей» для каждого параметра. Золотые числа 0,382 и 0,618 гармонию оптимальных «противоположностей» в рабочих величинах; они «присутствуют» в ССЦ всех рассматриваемых параметров в золотом режиме гипертензии. Величины b^k_j⁺¹, b^k_j^-1 и b^k_j представляют оптимальное соотношение «противоположностей» при различных уровнях гипертензии. Диапазон гипертензии b=1÷2 приблизительно постоянен для всех животных. При сравнении «пространств» ССЦ (2.28), (2.72) и (2.78) следует отметить важную особенность - их последовательное «вырождение». В первом «пространстве» величина j-параметра зависит от веса животных и уровня гипертензии, во втором – от «номера» сосуда в цепочке и гипертензии, в третьем же исчезает зависимость и от «номера» сосуда (остается только гипертензия). Во всех «пространствах» сохраняется зависимость j-параметра от внешнего фактора – физической нагрузки (гипертензии). Аналогия «пространств» (2.28), (2.72) и (2.78) заключается в том, что в условиях гипертензии их энергооптимальная гармония «противоположностей» обусловлена универсальными золотыми отношениями:

n_S(b) = 0,382b,

n_D(b) = 0,618/b,

где n_S(b), n_D(b) - соответственно отношение среднесистолической и среднедиастолической величин j-параметра, отнесенных к длительности сердечного цикла, к среднему за сердечный цикл значению параметра при различных уровнях гипертензии. Величины n_S(b) и n_D(b) в капиллярных ССЦ являются мерой энергооптимальной гармонии «противоположностей» в золотом и других режимах гипертензии.

Глава 3

ДОКАПИЛЛЯРНОЕ РУСЛО СЕРДЦА, ПРИНЦИП ОПТИМАЛЬНОГО ВХОЖДЕНИЯ И ГАРМОНИЯ «ПРОТИВОПОЛОЖНОСТЕЙ»

3.1. Интегратизм, системный подход и принцип оптимального вхождения

До последнего времени в естественных науках в качестве основного метода исследования доминирует редукционизм. Редукционизм предполагает необходимость разложения целого на составляющие его детали и механизмы. Углубляясь, разбивая сложное на простые составляющие (части) и исследуя их по отдельности, – таков путь редукционистского метода. Считается, что, сводя сложное к совокупности его частей, можно, изучив последние, получить сведения о свойствах исходного целого. Благодаря выдающимся успехам в исследовании вещественно-энергетических свойств природы, редукционистский подход прочно утвердился в психологии не только ученых, но и людей, далеких от науки. Анализируя сложившуюся обстановку в современной науке, лауреат Нобелевской премии И. Пригожин с сожаленьем отмечал: «…Цивилизация достигла необычайных высот в искусстве расчленения целого на части, а именно в разложении на мельчайшие компоненты. Мы изрядно преуспели в этом искусстве, преуспели настолько, что нередко забываем собрать разъятые части в единое целое (отмечено нами. В.Ц.), которое они некогда составляли» [124, с. 11]. В биологии метод редукции – расчленение целого (объекта) на все более мелкие части – получил широкое распространение. Однако на «редукционистском» пути возникли большие проблемы, поскольку сложившиеся стереотипы мышления не позволяют существенно сдвинуться в понимании так называемых «сложных систем», к числу которых относятся все живые системы. Как следствие редукционистского подхода к изучаемому объекту появляется феномен «исчезновения» свойств живого объекта. Например, специалист, изучив структуру и свойства ногтя мизинца, ничего не может сказать о свойствах и структуре ладони или, тем более, руки в целом. Отметим, организация взаимодействия всех подсистем организма, и не только организма, но и всей живой природы, в отличие от неживой, имеет в своей основе аспект «целесообразности». При следовании редукционистскому методу исследователь ничего не может сказать о природе «целесообразности» на более высоких уровнях, поскольку часть информации при дроблении неизбежно утрачивается. Академик В.П. Казначеев пишет по этому поводу: «Чем дальше вы расчленяете живые комплексы, тем дальше вы уходите от биологии и, в конце концов, вам остаются только …законы неживой природы» [75, с. 111]. Английский драматург Б. Шоу иронически отмечал: «Если в поисках истины исследователь будет все более дробить изучаемые объекты, то он рискует узнать все…ни о чем» [215, т. 6, с. 117]. Тем не менее, надежды многих ученых всего мира понять феномен жизни, исходя из принципов редукционизма, живы и по сей день. Однако, все более измельчая объект исследования, мы никогда не выйдем к знанию целого. Биологические науки испытывают острую потребность в «сборке» сложного из изученных частей.

Отметим, в противовес редукционистскому подходу еще в античные времена была сформулирована аксиома: целое больше суммы его частей. Сейчас она читается как аксиома эмерджентности (от английского слова emergence - возникновение, появление нового): несводимость свойств целого к сумме свойств его частей. Всякая живая система не является простой суммой своих составных частей, она всегда имеет особые свойства, отсутствующие у ее частей (подсистем). Кроме того, живая система не может не иметь своей внутренней структуры, своих законов взаимодействия частей, своей внутренней логики. Любое живое целое (система) создано Природой для выполнения определенной целесообразности (функции). Можно сказать, знание целого есть знание его цели и предназначения, знание же части живой системы есть знание того, как эта часть помогает целому в достижении ее цели. По мнению Ю. Г. Черепахина [205], должны существовать два неразрывных потока познания целого: 1) знание целого ведет нас к знанию части; 2) знание части углубляет нас в знании целого. Таким образом, основу такого подхода представляет последовательность: от целого – через части – к целому. Подход – через известные части – к целому – использован нами в этой главе (последовательная «сборка» сердечных объектов из ранее изученных частей). Можно сказать, что такой подход заложен в выдвинутом нами принципе оптимального вхождения «простых» систем в «сложные» [193].

Структурно все живые системы пришли к гармонии в результате длительной эволюции. Это положение никем не оспаривается. Однако и в наше время нет полного понимания того, согласно каким критериям в течение эволюции происходит самоорганизация - усложнение систем для достижения полной гармонии? Все согласны с тем, что «самоорганизация - процесс пространственно-временного упорядочения в открытой системе за счет согласованного взаимодействия множества элементов ее составляющих» [184]. Однако нет полного понимания механизмов самоорганизации. Проблемой самоорганизации, казалось бы, могла заняться физика, поскольку она является в настоящее время наиболее «продвинутой» из естественных наук. Однако «проблемы, возникающие при рассмотрении упорядоченности биологических структур, ее создания и эволюции, не лежат в области физики», поскольку «физика не претендует на объяснение природы..., (она) пытается объяснить лишь закономерности в поведении различных объектов» [16, с. 4]. Академик В.А. Энгельгардт [223, с. 220) писал, что «…физические законы помогают установить отдельные закономерности в биологических объектах и процессах, но они не могут объяснить причины именно такой организации живой системы, а не какой-либо другой». Очевидно, что невозможно свести функционирование окружающих нас живых систем только к взаимодействию атомов и элементарных частиц. Простейшая биологическая клетка, состоящая из известных атомов и молекул, подчиняющихся законам физики, тем не менее, для самой физики недоступна, по крайней мере, в том, что касается принципа ее жизнедеятельности. На сложность познания глубинных законов самоорганизации биосистем указывал В.А. Энгельгардт [223, с. 221): в биологии «…нам приходится оперировать главным образом сведениями феменологического характера. Более глубокие движущие силы, детализация механизмов их действия, каузальные и функциональные аспекты во многом еще остаются скрытыми». Мнение выдающегося биохимика по своей глубине не утратило своего значения и в наши дни. Естественно, нельзя познать законы и принципы организации «сложной» системы, не исследовав предварительно ее частей («простых» систем). В современной науке возникает течение, подразумевающее «сборку» объекта из ранее изученных частей. Это направление получило наименование «интегратизм». Интеграция (от лат. integratio – восстановление, восполнение) означает объединение, взаимопроникновение каких-либо (элементов) частей в целое. Как считал В.А. Энгельгардт [223, с. 207), основная сущность интегратизма состоит «в познании того, каким образом (отмечено нами. В.Ц.) происходит включение, интеграция элементов более примитивных в новые целостности, стоящие на более высокой ступени организационной иерархии, с иными степенями упорядоченности». В соответствии с принципом интегратизма исследователь должен идти в обратном редукционизму направлении. Этот метод предполагает последовательную сборку систем возрастающей сложности из ранее изученных элементов («простых» систем) по направлению от «простого» к «сложному». При этом последовательно восстанавливаются свойства целого, утраченные при «дроблении» объекта. Очевидно, что такой метод требует системного подхода к исследуемому объекту. В плане «сборки» наибольшее теоретическое и практическое значение для биологов представляет разработанный Ю.А. Урманцевым вариант общей теории систем [180, 181]. Урманцевым впервые, помимо универсальных понятий «объект» и «объект-система», введено понятие «закон композиции (организации)» объекта. «Объектом» по Ю.А. Урманцеву признается любой предмет мысли, т.е. предметы объективной и субъективной реальности, и не только вещи, но также качества, свойства, отношения, процессы и т.д. «Объект-система» – это единство, созданное определенного сорта «первичными» элементами + связывающими их в целое отношениями + ограничивающими эти отношения условиями (законом композиции). Для биолога выявление «закона композиции» равнозначно выявлению закона сопряжения частей «раздробленной» системы в единое целое. Урманцев не предлагает исследователю готового рецепта для «поиска» законов композиции (организации), это предстоит сделать самому исследователю. Однако введение Ю.А. Урманцевым аспекта композиции в определение системы имеет важнейшее значение, поскольку этому аспекту в биологических науках до сих пор не уделяется должного внимания. Организация живого объекта многими биологами все еще воспринимается как некая аксиоматическая данность Природы, которая не подлежит изучению. Однако невозможно говорить о гармонии объекта, не изучив предварительно организацию его частей на различных уровнях дробления!

При изучении всякой живой системы неизбежно возникает вопрос: «По какому критерию происходит слияние различных частей этого объекта в единое целое? Интегратизм (сборка), как мы уже отметили выше, идеологически связан с системным подходом, который приобретает в настоящее время все большее значение (особенно в биологии). Однако на этом пути возникают большие трудности. Для полноценной «сборки» живой системы необходимо иметь огромный объем экспериментальных данных, характеризующих различные стороны жизнедеятельности системы. Большинство известных биологических объектов по причине их исключительной сложности чаще всего изучены очень «мозаично». Вследствие этого нельзя выполнить достаточно полный и глубокий анализ подавляющего большинства живых систем. Сердце человека и млекопитающих в настоящее время является некоторым «исключением из правила». Оно в достаточной степени изучено и по «вертикали» (иерархия систем), и по «горизонтали» (множество параметров деятельности). Этот орган может быть не только подходящим объектом для «сборки», но также и «полем поиска» законов и критериев гармоничного включения «простых» систем в более сложные. На основе проведенного системного анализа большого объема экспериментальных данных нами впервые была установлена энергооптимальная основа сопряжения (гармонии) сердечных систем независимо от уровня их сложности [193, 194, 196]. Универсальность сопряжения «простых» систем в «сложной» представлена нами в «принципе оптимального вхождения»: «Каждая из «простых» сердечных систем, совместно образующих «сложную» сердечную систему, включена в последнюю оптимальным образом, вследствие чего сложная система исполняет свою функцию с минимальными затратами энергии и строительного материала». Этот принцип позволяет осуществить последовательную «сборку» (интеграцию) все более сложных систем. В соответствии с принципом оптимального вхождения оптимальность всякой «сложной» биосистемы (объект-системы) обусловлена оптимизацией включения в нее отдельных «простых» систем: конструктивных элементов, параметров, биологических процессов и т.д. Последовательная «сборка» все более сложных систем позволяет, в конечном счете, выявить законы гармонии сложного биообъекта в целом.

Согласно общей теории систем (ОТС) Урманцева любой параметр деятельности сердца можно представить в качестве объект-системы. Гармония в объект-системе (сердечном параметре) определяется как сопряжение представленных в ней элементов («противоположностей»). Отметим, «противоположности» имеют место в каждом сердечном параметре. Это обусловлено тем, что любой параметр имеет физиологический диапазон значений, в пределах которого нормальная деятельность сердца сохраняется. «Рабочая» величина параметра разделяет этот диапазон на два «противоположных» участка: участок больших и участок меньших возможных значений. По отношению к рабочей величине параметра первый из них можно обозначить как интервал «положительных» приращений, а второй как интервал «отрицательных». Граница между этими интервалами подвижна. Показано [183, с. 51], что живые организмы и их ведущие функциональные системы в процессе жизнедеятельности постоянно решают задачи поиска минимума затрат свободной энергии как при осуществлении своих специализированных функций, так и в процессе морфогенеза. Таким образом, осуществляется поиск точки оптимального разделения «противоположностей». Разделение физиологического диапазона для сердечных параметров всегда происходит оптимальным образом по отношению к внешнему «возмущению» [194]. Это означает, что внутри диапазона возможных при этом значений каждого параметра всегда «подбирается» такое соотношение «плюсовых» и «минусовых» участков, при котором обеспечивается наиболее экономная деятельность «сложной» сердечной системы.

Таким образом, принцип оптимального вхождения и гармония «противоположностей» «переплетены» в сердечных системах. Энергооптимальная гармония создается за счет поиска «противоположностей» в каждой из «простых» систем, образующих сложную систему. Этот «поиск» обусловлен критерием оптимального вхождения в сложную систему. Каждая «сложная» система, в свою очередь, является одной из «простых» в более сложной системе и т.д. При внешнем «возмущении» сопряженное изменение «простых» и «сложных» систем сердца происходит до тех пор, пока не будет достигнуто оптимальное «энергетическое» и вещественное совершенство всех так называемых «простых» и «сложных» систем.

3.2. Кислороднесущие системы, принцип оптимального вхождения и гармония «противоположностей»

Система крово-кислородного обеспечения сердечной мышцы имеет важнейшие значение для обеспечения нормальной деятельности сердца и всего организма. Эта система имеет «цель»: оптимальное сопряжение «количества» и «качества» кислорода, потребляемого в сердечных клетках. Отметим, сердце человека и других млекопитающих в покое потребляет около 10% от общего количества кислорода, потребляемого организмом, хотя вес сердца составляет всего около 0,6% от веса тела. Энергию, необходимую для совершения механической работы, сердце получает главным образом за счет распада углеводов и жиров с участием кислорода. При интенсивной мышечной работе коронарный кровоток может возрастать в четыре раза; примерно во столько же раз увеличивается потребление сердцем кислорода [193].

Математиками представлены несколько моделей кислородного обеспечения сердечной мышцы. Однако все существующие к настоящему времени математические модели страдают существенными недостатками. Даже в наиболее продвинутых моделях [261] не представлено сопряжение кислородных параметров в сердечной ткани с параметрами архитектоники и гемодинамики снабжающих микрососудов. Отсутствие этих параметров не позволяет в полной мере представить их вклад в сложную систему крово-кислородного обеспечения. Нашей задачей является выявить с учетом не рассматриваемых прежде параметров конечную «цель» Природы: «Почему эта система организована таким, а не иным образом?». Для решения этой задачи ниже нами произведена последовательная «сборка» системы кислородного обеспечения сердца по направлению «от простого к сложному». «Сборка» докапиллярного участка произведена по цепочке функционально связанных кислороднесущих систем возрастающей сложности: эритроцит → кровь → сосуд с движущейся кровью → гемососудистый тройник → генерации транспортных и обменных тройников → докапиллярное русло сердца. На каждом этапе во всех рассматриваемых системах будет представлена гармония «противоположностей».

3.2.1. Эритроцит

Первой по «простоте» кислороднесущей системой является эритроцит. Для всех позвоночных универсальным признаком является заключение гемоглобина в специальные клетки – эритроциты. Молекулы гемоглобина обладают способностью присоединять и отдавать молекулярный кислород. Основная масса эритроцита состоит главным образом из воды (65%) и молекул гемоглобина (34%). Отметим, что соотношение масс гемоглобина и воды близко к соотношению чисел Фибоначчи (1:2). Концентрация гемоглобина у разных видов млекопитающих одинакова; она не зависит от диаметра и объема эритроцитов и их возраста [88, 171].

«Вхождению» гемоглобина в эритроцит соответствует ряд конструктивных особенностей, аналогичных для различных видов млекопитающих:

1) оболочка эритроцита отделяет дыхательный пигмент от плазмы крови, что создает наиболее благоприятную ионную среду для выполнения клеткой специфических кислороднесущих функций;

2) внутри эритроцита концентрация гемоглобина достигает достаточно высокой степени, что необходимо для сохранения пигментом сложного строения, чтобы обеспечить ему кооперативный эффект и своеобразную форму кривой диссоциации оксигенированной его формы;

3) высокая концентрация гемоглобина внутри эритроцита и изоляция пигмента от плазмы позволяет резко повысить кислородную емкость крови без увеличения онкотического давления в плазме, что имеет огромное значение для обмена воды и электролитов между тканями и кровью в тканевых капиллярах;

4) кооперативное связывание кислорода повышает эффективность гемоглобина как переносчика кислорода [152];

5) процессы связывания и отделения кислорода гемоглобином не требуют энергетических затрат [171].

6) молекулы гемоглобина в эритроците имеют паракристаллическую упаковку; их концентрация в клетке близка к предельной [218].

Представленные особенности «включения» гемоглобина в систему «эритроцит» обеспечивают последнему эффективное взаимодействие с окружающей средой. Прежде всего, нахождение молекул гемоглобина внутри эритроцита обеспечивает по сравнению с растворением такого же количества гемоглобина в плазме уменьшение вязкости крови в несколько раз [188]. Естественной концентрации гемоглобина в крови (15 г на 100 мл) соответствует минимальная вязкость последней; даже небольшое увеличение концентрации гемоглобина резко увеличивает вязкость крови [214]. Эритроциты придают крови свойства неньютоновской жидкости, что обеспечивает значительное снижение вязкости при прохождении крови через цепочку микрососудов.

Вода представляет собою двойную структуру. Одна ее фракция имеет квазикристаллическую структуру, вторая – это обычная жидкая вода. Физическая особенность внутриклеточной воды заключается в ее упорядоченной, квазикристаллической структуре при одновременном сохранении свойства жидкой воды – низкого значения вязкости. Внутри клетки квазикристаллическая вода находится в состоянии максимальной упорядоченности – в состоянии, достигаемом в неживых системах только при абсолютном нуле. Это состояние связано с тем, что квазикристаллическая структура внутриклеточной воды при температуре около 38^оС непрерывно разрушается и непрерывно возникает заново в процессе расходования энергии метаболизма [171], т.е. происходят непрерывные фазовые переходы «противоположностей» (кристалл – жидкость) [171].

Добавим к вышесказанному, что вода - супрамолекулярная аквасистема, межмолекулярный континиум которой обеспечен единой динамической Н-системой водородных связей [146]. В аквасистемах клетки, ткани, органа имеет место оптимальное соотношение энергий организованных I(U) и хаотических S(U) форм движения. Вода способна сохранять уровень организованности своих фрагментов. На уровне клетки вблизи 38^оС организованной формой является жидкий лед, жидкая вода соответствует хаотической форме. Во всех аквасистемах здорового организма существует поддерживаемый уровень организованности i=I(U)/S(U), равный золотому числу i=1,62 [54]. Таким образом, энергии «противоположностей» (организованность и хаос) в аквасистемах здорового сердца соотносятся между собою по золотому сечению! Отметим, максимальная способность воды переходить в «противоположные» состояния в обоих направлениях соответствует «золотой» температуре 38^оС. Эта величина делит температурный диапазон воды по пропорции золотого сечения; при этой температуре создаются наиболее благоприятные условия для протекания процессов жизнедеятельности. Все неводные компоненты живой клетки (белки, нуклеиновые кислоты и т.д.) при обеспечении «квазикристаллической» температуры воды обладают термостабильностью при обмене веществ. Высокие теплофизические свойства воды обеспечивают стабильность среды в клетках и постоянство протекания биохимических процессов в последних при нормальных температурах в организме теплокровных животных. Таким образом, золотой уровень организованности «совмещен» с золотым разделением температурного интервала воды.

Молекулы гемоглобина располагаются на внутренней стороне мембраны эритроцита; между двумя молекулами гемоглобина находятся две молекулы воды. Вода в этой конструкции выполняет две взаимно «противоположные функции». С одной стороны, вода поддерживает жесткую структуру, что позволяет сохранять автономность каждой молекулы гемоглобина, с другой – обеспечивает изменчивость формы эритроцита. Равномерное распределение молекул гемоглобина в эритроците обусловливает равномерное распределение внутриклеточной воды. С другой стороны, внутриклеточная вода в эритроците образует сложную пространственную сеть и обладает, следовательно, квазикристаллической структурой. Энергия метаболизма безядерного эритроцита полностью расходуется для поддержания структуры внутриклеточной воды эритроцита в упорядоченном, квазикристаллическом состоянии [171].

Главная функция эритроцитов - транспорт кислорода к месту его потребления с последующим газообменом между кровью и окружающими тканями. Складирование гемоглобина под мембраной эритроцитов и эффективность движения последних в потоке крови обусловлены, прежде всего, особенностями формы эритроцитов. Оптимальная форма должна: 1) обеспечить при заданном объеме эритроцита «складирование» под мембраной максимального количества молекул гемоглобина; 2) обеспечить минимум потерь энергии при движении эритроцита в плазме крови. Этими двумя предварительными условиями обусловливается минимальная энергетическая «цена» транспорта кислорода.

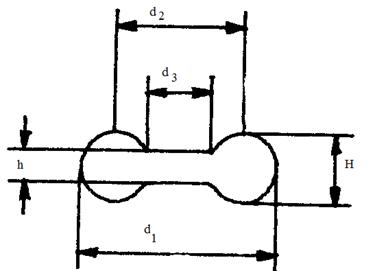
Рис 3.1. Дискообразная форма эритроцита человека. d₁=8 мкм- диаметр клетки; d₂=5 мкм- диаметр наиболее выпуклой части клетки; d₃ =3 мкм- диаметр вогнутой части клетки; Н=2 мкм– толщина выпуклой части клетки, h=1 мкм - толщина клетки.

У всех млекопитающих от крошечной землеройки до кита эритроциты имеют форму двояковогнутого диска. Диаметр эритроцитов у всех млекопитающих приблизительно одинаков и составляет 7-10 мкм. Для нас представляет интерес отношение поверхности мембраны эритроцита, под которой размещаются молекулы гемоглобина, к объему клетки. При анализе возможных дискообразных форм эритроцита при постоянном объеме было показано, что максимальное отношение его поверхности S к объему V соответствует естественной форме (для человека S/V=1,638) [284]. Молекулы гемоглобина располагаются непосредственно под мембраной эритроцита; их взаимное расположение соответствует предельно плотной, паракристаллической упаковке [218]. Таким образом, эритроцит имеет: 1) максимальное отношение S/V, 2) максимально плотную упаковку гемоглобина под мембраной. Максимальная концентрация гемоглобина, равная 34%, наблюдается у эритроцитов разных видов млекопитающих, причем эта концентрация не зависит от диаметра эритроцитов и их возраста [171]. Эритроцит транспортирует максимальное количество молекул гемоглобина, а, следовательно, и молекул кислорода. Следовательно, «складские» возможности эритроцита использованы в высшей мере эффективно. За счет этого доставка необходимого количества кислорода к месту потребления достигается при минимальном количестве «суденышек» (эритроцитов). Установлено [166], что оптимальная конструкция эритроцитов связана с числами Фибоначчи: 1, 2, 3, 5, 8 (см. рис. 3.1).

Большое значение для гемодинамики имеют механические свойства мембраны эритроцита. Показано [46], что при естественной форме эритроцита энергия, необходимая для деформации мембраны минимальна. Благодаря свойствам растяжимости мембраны движение эритроцитов в плазме происходит с минимальными затратами энергии; эритроциты движутся подобно капелькам жидкости [254].

При движении эритроцита в потоке происходит вращательно-поступательное движение мембраны вокруг содержимого клетки (оболочка эритроцита движется подобно гусенице танка) [315]. Таким образом, оптимальная форма мембраны обусловливает максимальную эластичность последней и минимум потерь энергии при движении отдельного эритроцита. Отметим, что такие замечательные особенности мембраны присущи лишь эритроцитам, «построенным» по числам Фибоначчи!

Хаотическое расположение эритроцитов в крови исключается [95, 208]; каждый эритроцит движется вдоль сосуда своей узкой стороной. Отметим, что дискообразная форма эритроцитов препятствует их оседанию на стенки сосуда [76]. При таком расположении, находясь в слоях плазмы с разными скоростями, эритроцит вращается вокруг своего центра симметрии по оси, перпендикулярной к его вогнутым сторонам.

Система морфологических и корпускулярных элементов крови окутана силовыми линиями электрического поля. Между отдельными элементами крови действуют силы электростатического распора, препятствующие полному сближению и соприкосновению эритроцитов. Дискоидная форма эритроцитов обеспечивает симметрию их движения по отношению к продольной оси сосуда; благодаря этому обстоятельству обеспечивается минимальная вязкость крови [335]. Таким образом, дискоидная форма эритроцита, «построенного» в соотношениях Фибоначчи, является оптимальным разрешением высоких требований к гемодинамическим параметрам этой клетки и крови в целом. Можно сказать, что форма клетки найдена как оптимальное сопряжение «противоположностей» параметров в сложной системе (эритроцит). Отметим, что в капиллярах и терминальных артериолах эритроциты - диски принимают парашютообразную форму [292]. Эритроциты выстраиваются в цепочку, которая перемещается в оболочке из плазмы. Бесклеточная краевая зона с низкой вязкостью образует слой, который значительно облегчает скольжение эритроцитов. Этот феномен противодействует увеличению вязкости крови при уменьшении скорости кровотока. Установлено [285a], что вязкость крови в каждом сосуде не возрастает, если скорость эритроцитов не опускается ниже 500 мкм/сек. однако даже в капиллярах скорость значительно выше критической.

Отметим «золотые» особенности в конструкции молекулы воды. Эта молекула имеет форму в виде буквы V. Для состояния льда отношение длин связей (Н-О) к (Н-Н) равно 0,100/0,163=0,613, в талой воде (Н-О)/(Н-Н) приближается к значению j=0,618, т. е. имеют место «золотые» соотношения [13, 194]. «Золотое» расположение атомов обусловливает особые свойства воды среди других жидкостей. Такая конструкция сильно отличает молекулу Н₂О от линейных молекул, в которой все атомы расположены цепочкой. Вода – единственная жидкость на Земле (кроме ртути), для которой зависимость удельной теплоемкости от температуры имеет минимум (см. рис. 3.2). Именно такое особое расположение атомов в молекуле воды и позволяет ей иметь множество необычных свойств. Вода внутри клетки находится в состоянии максимальной упорядоченности, достигаемой в неживых системах только при абсолютном нуле. Отметим, что теплоемкость воды при золотой температуре 38^оС незначительно отличается от минимальной при температуре 36,8^оС. Вода при температуре 38^оС в клетках обладает особой, квазикристаллической упорядоченностью, при которой количество разорванных и сохранившихся тетрамерных связей примерно одинаково [87]. При «золотой» температуре 38^оС выравниваются массы квазикристаллической

рис3,2

Рис. 3.2. Зависимость теплоемкости воды от температуры [23]. Интервал t^oC = 26,7 – 43^oC соответствует интервалу жизни биосистем.

воды (жидкий лед) и обычной воды, при этом способность воды переходить из одного состояния в другое (т.е. обмен информацией) максимальна. Такое соотношение обеспечивает равновероятное протекание биопроцессов в обоих направлениях. Температура 38^оС обеспечивает в эритроците условия теплового комфорта, в условиях которого на поддержание оптимальной температуры в клетке расходуется минимальная энергия (см. рис. 3.2). Вблизи этой температуры кровь при гематокрите Ht=42% имеет минимальную вязкость [166]. Температура на участке 36,8 - 38,2^оС оптимальна для течения ферментативных реакций [53]. При превышении температуры 38,2^оС скорость ферментативных реакций начинает снижаться вследствие разрушения вторичных и третичных структур фермента. Таким образом, «золотая» температура является рабочей температурой, которая удовлетворяет, как мы могли убедиться, оптимальной гармонии «противоположностей» многих параметров не только эритроцита, но и крови в целом.

В большинстве «простых» систем эритроцита имеют место золотые «противоположности». Оптимальное «вхождение» «противоположностей» каждого из гемодинамических и структурных, а также температурного, параметров в систему «Эритроцит» обеспечивает свой «вклад» в максимальную экономию энергии и вещества в системе «Кровь».

3.2.2. Кровь

Основными элементами крови являются плазма, эритроциты, лейкоциты и тромбоциты. Два последних элемента не имеют отношения к транспорту кислорода, поэтому мы не будем их рассматривать. Будет произведен анализ «вхождения» в кровь первых двух элементов: эритроцитов и плазмы.

Оптимальная величина концентрации эритроцитов в крови обусловлена двумя противоположными требованиями. С одной стороны, желательно иметь высокую концентрацию эритроцитов, поскольку при этом возрастает количество кислорода в единичном объеме крови. С другой стороны, неограниченный рост гематокрита связан с повышением вязкости крови, а, следовательно, и с возрастанием расхода механической энергии на транспорт кислорода. Это противоречие устраняется [203, 293], если отношение вязкости крови ξ к гематокриту Ht минимально (см. рис. 3.3). Такое оптимальное отношение соответствует естественной величине Ht=42% при нормальном артериальном давлении и нормальном напряжении сдвига τ=10³ дн/см² [242]. По расчетам И.Ф. Образцова и М.А. Ханина [113] величине Ht=42% соответствует оптимальная концентрация эритроцитов С=5,2·10⁹ 1/мл крови. Экспериментально установлено [246], что минимальная «цена» транспорта единичного объема кислорода в сосудах приблизительно соответствует естественной величине гематокрита. Гематокрит, определенный путем центрифугирования порции крови из артериол и венул диаметром 100-200 мкм, равен постоянной величине, которая почти не отличается от гематокрита в магистральных сосудах [229, 281]. Таким образом, оптимальное соотношение «твердой» (эритроциты) и «жидкой» (плазма) составляющих крови остается постоянным по всему коронарному руслу. «Оптимальная» величина гематокрита одновременно обусловливает оптимальность реологических свойств крови и объема транспортируемого кислорода. «Рабочая» величина этого параметра оптимальным образом разделяет возможный диапазон вязкости крови и возможный диапазон концентрации эритроцитов. Вследствие оптимальной гармонии «противоположностей» этих параметров на транспорт единичного объема кислорода по коронарному руслу тратится минимальное количество энергии. Установлено [281], что естественное соотношение объемов эритроцитов и плазмы соответствует отношению средней скорости эритроцитов к средней скорости пристеночного слоя плазмы, равном 1,6 (золотое число!). «Золотое» соотношение скоростей эритроцитов и плазмы, соответствующее оптимальному соотношению гематокрита и вязкости крови, обеспечивает согласованное по времени движение «твердых» и «жидких» компонентов крови в каждом сосуде. Кровь млекопитающих на 80% состоит из воды. Отметим, потребность в энергии, расходуемой на поддержание температуры самого теплоносителя при 38°С минимальна [166]. При этой температуре выравниваются массы квазикристаллической воды (жидкий лед) и обычной воды [87]. Этот феномен обеспечивает равновероятность течения обратимых биохимических реакций в обе стороны. Добавим к этому, вода имеет высокую теплопроводность и теплоемкость. Благодаря первому свойству тепло от химических реакций равномерно распределяется по объему крови (при этом устраняется «перегрев» и «недогрев»); вследствие большой теплоемкости даже для небольшого повышения температуры требуется большое количество энергии. Тем самым тепловые свойства воды обеспечивают постоянство протекания биохимических процессов в крови и ее температурную стабильность. Как отмечали Эйген и Винклер (220, с. 96), «в живых организмах скорость химических реакций всегда достигает предельного значения, которое определяется законами физики». При «золотой» температуре 38^оС в плазме крови существуют наиболее благоприятные условия для протекания биологических процессов с максимально возможной скоростью.

Подытожим. Минимизация затрат механической энергии на перемещение крови происходит благодаря минимизации вязкости последней (оптимальная форма и оптимальная концентрация эритроцитов, симметрия кровотока, оптимальная температура). С другой стороны, за счет оптимальной формы эритроцитов и паракристаллической упаковки молекул гемоглобина обеспечивается максимально возможная концентрация дыхательного пигмента в единичном объеме крови. Оптимальное «вхождение» «противоположностей» каждого из этих параметров в систему «Кровь» обеспечивает минимум потерь механической энергии на перемещение единичного объема кислорода к месту его потребления. Естественно, что все представленные оптимальные «рабочие» значения параметров одновременно характеризуют реологические свойства крови и объем транспортируемого кислорода. Естественно, все рассмотренные нами особенности вхождения «противоположностей» в систему «Кровь» имеют место во всех органах организма (в том числе и в сердце).

Интересно добавить, что установлена связь элементов крови с золотой пропорцией и числами Фибоначчи [145]. Форменные элементы крови - «кислородные» (эритроциты) и «некислородные» (лейкоциты и тромбоциты) - в глобулярном объеме крови сбалансированы как соотношение чисел 62:32:6. Нетрудно увидеть, что отношение «противоположностей» - «кислороднесущей» и «некислородной» - равно золотому числу 1,618. Можно сказать, что и здесь налицо золотая гармония «противоположностей» в элементах, несущих кислород, и элементах, имеющих «некислородное» назначение. Было также показано отношение «противоположностей»: объема циркулирующей крови к плазматическому объему в организме равно 5:3, а отношение плазматического объема к глобулярному – 3:2 (числа Фибоначчи). Кроме того, А.Г. Суббота [166] показал, что соотношение «противоположностей» - эритроцитов трансформированной и дискоидной форм - также приблизительно составляет золотое сечение - 38,2 и 61,8%. С большой степенью вероятности можно предположить, что и за этими «золотыми» соотношениями скрываются дополнительные аспекты экономии энергии и вещества.

3.2.3. Сосуд с движущейся кровью

В сосудах с движущейся кровью расход энергии можно разделить на «механическую» и «химическую» составляющие. Механическая энергия тратится на перемещение крови в сосуде, а «химическая» расходуется на биопроцессы в крови. Рассмотрим механическую составляющую. Выше нами были представлены общие пути оптимизации вязкости крови: «подбор» формы эритроцитов, гематокрита и температуры. Однако в сосуде имеют место дополнительные факторы минимизации вязкости, связанные с движением эритроцитов. Дискообразная форма эритроцитов обеспечивает симметричное движение последних относительно продольной оси сосуда, что создает дополнительное снижение вязкости крови [335]. Таким образом, минимальная величина вязкости крови в сосуде обусловлена не только оптимальным «подбором» гематокрита, температуры и формы эритроцитов, но также и симметрийным способом движения последних. Наблюдения показали высокоупорядоченное распределение клеточных и плазменных компонентов в крови. Более легкие и мелкие компоненты крови находятся у стенок сосудов, а самые тяжелые смещены к продольной оси; тем самым обеспечиваются минимальные потери энергии на трение потока у стенок сосудов. Существуют и другие аспекты экономии механической энергии в сосуде. Установлено [94, 95], что движение крови в артериях имеет ламинарно-спиральный характер (можно провести некоторую аналогию с движением пули в стволе с винтовой нарезкой). Движение такого рода обеспечивается спиралевидной ориентацией мышечных волокон в стенках артерий [94]. Спиральный тип движения универсален и происходит c минимальной потерей энергии [43, 290]. Давно известно, что спирализация конструкций и процессов способствует экономии энергии и материала, обеспечивает повышенную прочность системы и надежность ее функционирования. Установлено также соответствие ориентации эндотелиальных клеток протекающему кровотоку [288]. Таким образом, налицо различные аспекты минимизации «механической» части общей энергии, расходуемой в сосуде (гематокрит, температура, симметрирование кровотока и спирально-ламинарный характер движения). Отметим также, что в сердечных сосудах имеют место синхронные пульсации стенки сосудов и кровотока. Частоты пульсации в стенке сосуда и потоке крови совпадают, между ними возникает резонанс. Резонанс между стенкой и кровью обеспечивает дополнительную минимизацию затрат энергии по перемещению крови в сосудах [173]. Таким образом, при движении крови в сосудах за счет рассмотренных аспектов обеспечивается дополнительная экономия механической энергии.

Необходимо рассмотреть соотношение затрат механической и «химической» мощностей при постоянном кровотоке в сосуде при изменении диаметра последнего.

Механическая мощность, расходуемая в сосуде с движущейся кровью (см. рис. 3.4),

W_M = 128Q²ξl/πd⁴,

где Q – кровоток, ξ – вязкость крови, l, d – длина и диаметр сосуда.

«Химическая» мощность, потребляемая в сосуде:

W_X = (π/4)bd²l,

где b– расход химической энергии в единичном объеме крови за единицу времени.

Рис. 3.4. Сосуд с движущейся кровью. q- объемный кровоток, d, l- диаметр и длина сосуда, ξ - вязкость крови, b - удельный расход химической энергии за единицу времени.

Даже при первом взгляде на эти формулы очевидно, что механическая и химическая составляющие суммарной мощности зависят от диаметра в различной степени. Более того, при изменении величины диаметра они изменяются в противоположных направлениях. Следовательно, при заданной величине кровотока q минимальный суммарный расход «противоположных» мощностей - механической и химической - должен соответствовать некоторому оптимальному диаметру d. Режим движения кровотока в сосуде при минимальном суммарном расходе мощности получил обозначение - режим «минимальной работы» [295].

В золотом режиме гипертензии с учетом диаметра d(b_ЗС), длины сосуда l(b_ЗС) и времени нахождения эритроцитов в сосуде t(b_ЗС) объемный кровоток q(b_ЗС) можно представить следующим выражением:

q(b_ЗС) = (π/4)d(b_ЗС)²l(b_ЗС)/t(b_ЗС).

В соответствии с расчетами Мюррея в этом режиме объемный кровоток в сосуде связан с его оптимальным диаметром и параметрами крови [295]:

q(b_ЗС)/d(b_ЗС)³ = (π/32),

где b(b_ЗС) – расход химической энергии в единичном объеме крови за единицу времени, x(b_ЗС) - вязкость крови в золотом режиме гипертензии.

Минимизация суммарного расхода энергии имеет место, если

/8 = l(b_ЗС)/d(b_ЗС)t(b_ЗС).

Отметим, энергооптимальное сопряжение «противоположных» мощностей имеет место во всех сердечных сосудах [216, 203].

Оптимальное соотношение механической и химической мощностей равно постоянной величине для всех сердечных артерий, артериол и капилляров не только в покое, но и при различных уровнях физической нагрузки [203]:

g(b_ЗС) = W_M(b_ЗС)/W_X(b_ЗС) = W_M(b)/W_X(b)= 0,5.

Таким образом, энергооптимальная гармония «противоположных» мощностей во всех сердечных сосудах представлена постоянным числом. Оптимальное сопряжение «противоположных» мощностей обусловлено энергооптимальными «противоположностями» в архитектонических, гемодинамических, температурных и «химических» параметрах. Вследствие этого, энергетическая «цена» транспортируемого кислорода в каждом сердечном сосуде имеет минимальную величину. Добавим к этому, что механическая и химическая «противоположности» соотносятся между собою как числа Фибоначчи (1:2).

3.3. Бифуркация – оптимальный вариант ветвления докапиллярных сосудов

Бифуркация является общим типом разветвления для всех коронарных артерий, включая и артериолы [358]. Любая бифуркация (тройник) является «сложной» системой, в которую ствол и каждая из ветвей включены в качестве «простых» систем. Особенность конструкции тройника состоит в том, что каждая его ветвь является стволом следующего тройника. Совокупность тройников образует артериальное «дерево» (см. рис. 3.5).

Докапиллярное русло сердца (артериальное «дерево») включает в себя сосуды эластического и мышечного типа, а также микрососуды. Диаметр эластических артерий превышает 500 мкм. Сосудами мышечного типа принято считать артерии с диаметром от 100 до 500 мкм. В обменные генерации входят микрососуды - артериолы с диаметром менее 100 мкм [111]. По отношению к транспорту и потреблению кислорода докапиллярное русло можно разделить на два «противоположных» участка. Первый участок составляют эластические и мышечные сосуды; по этим сосудам осуществляется транспорт кислорода к обменному участку. На втором, микрососудистом, участке происходит диффузия кислорода в окружающие ткани. Транспортные сосуды сердца (d>100 мкм) всегда разветвляются на асимметричные ветви. Обменные микрососуды, напротив, имеют симметричное ветвление. Особенности архитектоники бифуркационных тройников в золотом режиме гипертензии можно представить следующими коэффициентами [216]:

k(b_ЗС) = [d₁(b_ЗС)² + d₂(b_ЗС)²]/d_С(b_ЗС)²,

Fig35

Рис. 3.5. Артериальное дерево

1) коэффициент ветвления

2) коэффициенты относительного сечения ветвей

H₁(b_ЗС) = d₁(b_ЗС)²/[d₁(b_ЗС)² + d₂(b_ЗС)²],

H₂(b_ЗС) = d₂(b_ЗС)²/[d₁(b_ЗС)² + d₂(b_ЗС)²],

Из этих сотношений следует [193]:

d₁(b_ЗС) = d_С(b_ЗС), (3.1)

d₂(b_ЗС) = d_С(b_ЗС). (3.2)

Отметим, что для сердечных тройников величина k(b_ЗС) находится в пределах 1<k(b_ЗС)£1,26 (режим «минимальной работы») [216]. В диапазоне 1<k(b_ЗС)£1,26 имеет место оптимальное сопряжение диаметров ствола и ветвей [131]:

d₁(b_ЗС)³+ d₂(b_ЗС)³= d_С(b_ЗС)³. (3.3)

Соотношение (3.3) соответствует минимальному расходу мощности, израсходованной в каждом сосуде тройника на диссипацию кровотока и биохимические процессы в крови [131].

Представим доказательства того, что бифуркация является оптимальным вариантом ветвления сердечных сосудов по сравнению с трифуркацией, тетрафукарцией и т. д. Рассмотрим в качестве сравнения наиболее близкие варианты ветвлений - бифуркацию (ствол и 2 ветви) и трифуркацию (ствол и 3 ветви). Предварительно примем равные условия для обоих вариантов:

1) одинаковая разность давлений между аортой и артериальным концом капилляров;

2) равенство кровотока в первой коронарной артерии;

3) одинаковый диаметр первой коронарной артерии и одинаковый диаметр капилляров;

4) одинаковая вязкость крови во всех сосудах;

5) одинаковая плотность капиллярной сети;

6) в стволе и ветвях бифуркационных и трифуркационных тройников имеет место оптимальный режим «минимальной работы»;

7) суммарные величины расхода энергии, объема крови в сосудах и проводимости на докапиллярном участке одинаковы для обоих вариантов.

Для упрощения расчетов примем на докапиллярном участке все бифуркационные и трифуркационные разветвления симметричными и вязкость крови во всех сосудах одинаковой. Коэффициент конструкции всякого сосуда для обоих видов разветвления будем также считать одинаковым (C=l/d =const).

Исходя из условия C=l/d =const и условия энергооптимальности для каждого трифуркационного разветвления в золотом режиме гипертензии имеем:

d₁(b_ЗС)³+ d₂(b_ЗС)³+ d₃(b_ЗС)³= d_С(b_ЗС)³, (3.4)

l₁(b_ЗС)³+ l₂(b_ЗС)³+ l₃(b_ЗС)³= l_С(b_ЗС)³, (3.5)

где d_С(b_ЗС), d₁(b_ЗС), d₂(b_ЗС), d₃(b_ЗС), l_C(b_ЗС), l₁(b_ЗС), l₂(b_ЗС), l₃(b_ЗС) - соответственно диаметр и длина ствола и 1, 2 и 3 ветвей.

При симметричном бифуркационном ветвлении

d₁(b_ЗС) = d₂(b_ЗС) = 0,794d_С(b_ЗС), (3.6)

l₁(b_ЗС) = l₂(b_ЗС) = 0,794l_С(b_ЗС). (3.7)

Соответственно, при симметричной трифуркации

d₁(b_ЗС) = d₂(b_ЗС) = d₃(b_ЗС) = 0,694d_С(b_ЗС), (3.8)

l₁(b_ЗС) = l₂(b_ЗС) = l₃(b_ЗС) = 0,694l_С(b_ЗС). (3.9)

Покажем преимущества бифуркации на примере сердца собак. При бифуркации общее число докапиллярных генераций сердца N=28 [194]. Исходя из условий 1) – 3) и зависимости (3.8) при трифуркации для собак общее число докапиллярных генераций должно было бы равняться 18; по сравнению с бифуркацией количество этих генераций уменьшается в 1,6 раз. В соответствии с условиями (1) - (7), общий кровоток, общий объем крови и общая проводимость бифуркационных и трифуркационных сосудов, начиная от аорты до капилляров, принимаем равными. Для выполнения этих условий давление на каждом «трифуркационном» сосуде и его длина должны возрасти в 1,6 раза. При таком условии суммарный объем крови и суммарная проводимость для обоих вариантов ветвления будут равными. Однако при этом плотность обменных микрососудов в бифуркационном варианте больше, чем в трифуркационном, что имеет большое значение для наиболее эффективного кислородного обеспечения миокарда. Рассмотрим на примере сердца собаки, как осуществляется это преимущество. При соблюдении условия 5) количество обменных сосудов в каждой «одноименной» m-генерации (начиная от капилляров) при бифуркации будет больше, чем при трифуркации. К этому необходимо добавить, количество «трифуркационных» генераций в пределах кислородотдающего участка (7<d<40 мкм) всего 6 (при бифуркации - 9) [203]. Таким образом, в пределах диапазона 7<d<40 мкм при бифуркации имеет место наибольшее количество обменных микрососудов. Эти микрососуды совместно с капиллярами образуют общую обменную сеть максимальной плотности.

Рассмотрим другое «кислородное» преимущество бифуркации. В «одноименных» m-генерациях, начиная от капилляра (m=1, 2, 3 и т.д.), диаметр сосудов возрастает тем быстрее, чем больше число разветвлений. Например, в первой от капилляров «одноименной» генерации при бифуркации d₁(b_ЗС) = 1,26d_k(b_ЗС), при трифуркации - d₁(b_ЗС) = 1,44d_k(b_ЗС), при тетрафуркации - d₁(b_ЗС) = 1,59d_k(b_ЗС) и т. д. Скорость отдачи кислорода отдельным эритроцитом в двух соседних сосудах обратно пропорциональна соотношению их поперечных сечений (см. раздел 3.6). Очевидно, что соотношение соседних площадей в одноименных сосудах при трифуркации больше, чем при бифуркации. Следовательно, отдельный эритроцит в поперечном сечении трифуркационного m-сосуда отдает за единицу времени кислорода меньше, чем в «одноименном» бифуркационном. Чем дальше от капилляров, тем больше снижается скорость отдачи кислорода в «трифуркационном» сосуде по сравнению с «одноименным» бифуркационным. Можно показать с учетом условий 1) - 7), что время пребывания отдельного эритроцита в одноименных «бифуркационном» и «трифуркационном» сосудах приблизительно одинаково. Однако «трифуркационный» эритроцит за время пребывания в обменных сосудах отдает кислорода меньше, чем «бифуркационный». На участок в пределах d=7¸40 мкм приходится приблизительно 9 «обменных» бифуркационных разветвлений, а трифуркационных – всего шесть. Вследствие этого «бифуркационный» эритроцит при перемещении до капилляра отдает 12% кислорода, а «трифуркационный» только 8,3% [203]. «Трифуркационный» эритроцит при прохождении цепочки обменных сосудов не успевает «разрядиться» до «бифуркационного» напряжения на артериальном конце капилляра (рО_2кап=50 мм рт. ст.). Как следствие, должен уменьшиться докапиллярный «резерв» DpO₂ = 95 - рО_2кап, существуемый при бифуркации. Это означает, что при трифуркации снижается верхний предел физической нагрузки, при котором сердечная мышца еще получает адекватное кислородное обеспечение. Очевидно, что при дальнейшем росте ветвлений (n = 4, 5 и т. д.) уровень допустимой предельной нагрузки будет последовательно снижаться. При бифуркации предел допустимой нагрузки имеет наибольшую величину. Теоретически возможен еще один вариант ветвления - сквозной, при котором ветвления отсутствуют, а все сосуды (включая и капилляры) имеют одинаковый диаметр. При таком варианте кислородное обеспечение миокарда было бы крайне неэффективным. Таким образом, «кислородные» преимущества бифуркационного разветвления очевидны.

С бифуркацией связано еще одно важное преимущество. Бифуркации в каждой «одноименной» генерации обменных сосудов соответствует наименьшая величина диаметра. Следовательно, величина отношения поверхности к объему сосуда (S/V=4/d) в «одноименных» генерациях при бифуркации всегда будет больше, чем в любом другом варианте ветвления. Максимальные величины этого отношения обеспечивает наиболее высокий уровень метаболизма между кровью и сердечными клетками. Кроме того, при бифуркации на участке 7<d<40 мкм суммарная боковая поверхность обменных сосудов значительно больше, чем при трифуркации, тетрафуркации и т. д., что позволяет дополнительно увеличить объем продуктов метаболизма за единицу времени. Таким образом, из всех возможных вариантов ветвления (n=1, 2, 3, 4…) Природа «выбрала» бифуркацию (n=2) как наиболее эффективную конструкцию для обмена между кровью и сердечной тканью. Добавим к нашему анализу, что в математическом исследовании морфологии ветвления микрососудов, проведенном В.А. Глотовым в замечательной книге [47], математически показана неэффективность ветвления сосуда более чем на две ветви.

Установлено [241, 242], что в пределах 1<k£1,26 в тройниках имеет место минимальный суммарный расход сосудистого вещества. Также показано [272, 273], что при заданном кровотоке в стволе и заданном давлении между входом ствола и концами ветвей в режиме «минимальной работы» общий объем крови в сосудах тройника имеет минимальную величину. Таким образом, конструкция оптимальных бифуркационных тройников позволяет пропускать кровоток не только с минимальными затратами энергии, но и с использованием минимального объема сосудистого материала и минимального «заполняющего» объема крови. Очевидна также важность «подбора» длины сосудов в оптимизации коронарного русла. Ветвления тройников «по длине» вплоть до 100 мкм асимметричны; ветви меньшего диаметра имеют большую длину (см. рис. 2.5).

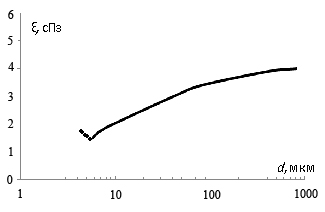
Рис. 3.6. Зависимость кажущейся вязкости ξ от диаметра микрососуда d [242].

За счет «подбора» длины асимметричных ветвей в конечном счете обеспечивается: 1) приблизительное равенство давлений на входе микрососудов, 2) одинаковое по суммарному времени продвижение всех эритроцитов, одновременно поступивших из аорты в первую коронарную артерию, до входа в «свой» микрососуд (см. раздел 2.5.5). В дальнейшем в симметричных ветвях обменных тройников (l₁(b_ЗС)=l₂(b_ЗС)) происходит синхронное движение «исходных» эритроцитов. Таким образом, в каждом сосуде имеет место оптимальное соотношение между диаметром и длиной; за счет этого обеспечиваются оптимальные условия движения крови по всему докапиллярному руслу. «Противоположные» типы ветвления в эластических и мышечных (асимметрия) и обменных тройниках (симметрия) создают гибкую структуру, которая позволяет обеспечить энергооптимальный транспорт адекватного объема кислорода в различные по уровню потребления регионы сердца. «Асимметричный» и «симметричный» участки имеют в основе оптимальную гармонию «противоположностей», которая обеспечивает адекватное кислородное снабжение по «качеству» и «количеству» по всему объему миокарда. Этот вопрос подробно рассмотрен нами в разделе 2.5.5.

В заключение можно сказать, что при одинаковом общем расходе энергии, крови и сосудистого материала на докапиллярном участке бифуркация по сравнению с другими вариантами ветвления позволяет создать максимальную плотность обменныхмикрососудов. Более того, в этом варианте в докапиллярных обменных сосудах обеспечивается наиболее интенсивный метаболизм между кровью и сердечными клетками. Энергооптимальная бифуркация соответствует оптимальному сопряжению «противоположностей» - транспортной и обменной частей докапиллярного участка коронарного русла, что имеет следствием наиболее эффективное кислородное обеспечение сердечной мышцы.

3.4. Обменный участок коронарного русла

3.4.1. Особенности конструкции обменных микрососудов

Микрососуды конструктивно отличаются от эластических и мышечных артериальных сосудов. Стенки этих сосудов имеют жесткую конструкцию, они мало или практически совсем не растягиваются. Общая поверхность и протяженность сосудов обменного участка в десятки раз больше таковых на транспортном участке. Отметим еще одно важное отличие. В соответствии с феноменом Фареуса-Линдквиста вязкость крови в крупных, средних и мелких артериях транспортного участка практически постоянна и не зависит от диаметра вплоть до d=100 мкм. Сосудам на обменном участке (d=7-100 мкм), напротив, сопутствует значительное снижение вязкости крови (см. рис. 3.6). Отметим поразительное сходство конфигурации и размеров микрососудов млекопитающих, несмотря на значительное различие по массе тела [76].

3.4.2. Обменные тройники в золотом и других режимах гипертензии

Рассмотрим особенности архитектоники обменных тройников. Теоретически показано и экспериментально подтверждено [216], что сердечные тройники имеют энергооптимальную конструкцию (1<k≤1,26). В обменных сердечных тройниках ветвления терминальных артериол приблизительно симметричны [49, 216]. Ветви каждого обменного тройника приблизительно одинаковы по длине и диаметру; при этом k(b_ЗС)»1,26, H₁(b_ЗС)»H₂(b_ЗС)=0,5. С учетом перечисленных особенностей и того, что эритроциты в микрососуды поступают при приблизительно одинаковом давлении, следует сделать вывод об одинаковости гемодинамических параметров для сосудов «одноименной» генерации. При сопоставлении экспериментальных зависимостей x = f(d) [242] и коэффициента конструкции сосуда С=j(d, l) для сердца [216, 193] нами установлено обратно пропорциональные относительные изменения вязкости крови и длины обменных сосудов в каждой из ветвей по отношению к стволу. По мере уменьшения диаметра обменных артериол вплоть до капилляров коэффициент конструкции (l/d) и время пребывания эритроцитов в каждом из них постепенно возрастают вдвое, а вязкость крови, напротив, в этом диапазоне постепенно снижается приблизительно в 2 раза [193].

Пульсовые колебания стенки по мере снижения калибра коронарных сосудов быстро угасают [300, 224], а в микрососудах практически отсутствуют. Вследствие указанных особенностей можно считать диаметр и длину микрососудов, а также величины вязкости крови x(b_ЗС), давления ΔP(b_ЗС) и кровотока Q(b_ЗС), неизменными в течение всего сердечного цикла как в покое, так и при любом уровне гипертензии. Вследствие этого обстоятельства нет необходимости в раздельном анализе систолической и диастолической составляющих рассматриваемых параметров. В дальнейшем для анализа будут использованы значения, усредненные за сердечный цикл.

С учетом симметрии обменных тройников параметры ствола и ветвей соотносятся следующим образом [203]:

d₁(b_ЗС)= d₂(b_ЗС)=0,794d_С(b_ЗС), (3.10)

l₁(b_ЗС)= l₂(b_ЗС)= 0,794[С₁(b_ЗС)/С_С(b_ЗС)]l_С(b_ЗС), (3.11)

ξ₁(b_ЗС)=ξ₂(b_ЗС)= [C_C(b_ЗС)/C₁(b_ЗСξ)]_C(b_ЗС), (3.12)

t₁(b_ЗС)=t₂(b_ЗС) = [С₁(b_ЗС)/С_С(b_ЗС)]t_C(ξ_ЗС), (3.13)

где d_С(b_ЗС), d₁(b_ЗС), d₂(b_ЗС), l_С(b_ЗС), l₁(b_ЗС), l₂(b_ЗС), ξ_C(ξ_ЗС), ξ₁(ξ_ЗС), ξ₂(ξ_ЗС), С_С(b_ЗС), С₁(b_ЗС), С₂(b_ЗС) – соответственно диаметр, длина, вязкость крови и время пребывания эритроцитов, коэффициент конструкции ствола, 1 и 2 ветвей в золотом режиме гипертензии.

Гемодинамические параметры ветвей по отношению к стволу с учетом (3.10-3.13):

q₁(b_ЗС) = q₂(b_ЗС)= 0,5q_C(b_ЗС),

G₁(b_ЗС) = G₂(b_ЗС)= 0,5G_C(b_ЗС),

DP₁(b_ЗС) = DP₂(b_ЗС)= DP_C(b_ЗС),

где q_C(b_ЗС), q₁(b_ЗС), q₂(b_ЗС), G_С(b_ЗС), G₁(b_ЗС), G₂(b_ЗС), DP_С(b_ЗС), DP₁(b_ЗС), DP₂(b_ЗС) – соответственно кровоток, проводимость и давление ствола, 1 и 2 ветвей в золотом режиме гипертензии.

Исходя из расчетов, представленных в работе [203], на каждом обменном j-микрососуде DP_j(b_ЗС) = 3,5 мм рт. ст. Следовательно, в каждом обменном тройнике

DP₁(b_ЗС) = DP₂(b_ЗС)= DP_C(b_ЗС). (3.14)

Аналогия давлений имеет большое значение для движения крови; за счет этого феномена время пребывания эритроцитов в «одноименных» обменных сосудах одинаково.

Среднее давление в аорте P_i(b_ЗС) в зависимости от веса i-животного можно определить из следующего соотношения [284]:

P_i(b_ЗС)=1,47 10⁵W_i^0,033,

где [P_i] ==дн/см², [W_i]= кг. Очевидно, что давление в аорте слабо зависит от веса животных: при изменении веса в 10⁵ раз давление увеличивается всего в 1,6 раз (см. Табл. 3, столбец 3). В то же время давление, приложенное к

Таблица 3. Зависимость гемодинамических и архитектонических параметров сердца от веса млекопитающих [198]

W, кг	N	P_i(β_ЗС), мм рт. ст.	Q_л(β_ЗС), мл с^-1	d(β_ЗС) мкм	DP_j(β_ЗС) мм рт. ст.
0,1	22,8	100	0,014	1035	3,62
1,0	25,4	108	0.087	1902	3,56
10	28,1	117	0,563	3543	3,54
100	30,8	126	3,64	6595	3,52
10³	33,5	136	23,49	12270	3,52
10⁴	36,2	146	151,6	22830	3.55
10⁵	38,9	162	979,2	42250	3,59

Примечания. W – вес животного, N – количество докапиллярных ветвлений, P_i(β_ЗС) – среднее артериальное давление, Q_л(β_ЗС) – средний коронарный кровоток в левой коронарной артерии, d_л(β_ЗС) – средний диаметр левой коронарной артерии, ΔP_j(β_ЗС) – давление, приложенное к j–сосуду в золотом режиме гипертензии.

каждому сердечному сосуду млекопитающих, практически одинаково (см. Табл.3, столбец 6). Расчетная величина давления ΔP_j(β_ЗС) в таблице совпадает с величиной, полученной нами для микрососудов.

Установлено [84], что даже при значительной физической нагрузке прекапиллярные сосуды практически не удлиняются и не расширяются. Следовательно, для ствола обменного тройника при гипертензии d_С(b)=d_С(b_ЗС), l_С(b)=l_С(b_ЗС) и ξ_С(b)=ξ_С(b_ЗС). Как представлено в разделах 2.7.1 и 2.72, в золотом и других режимах гипертензии для обменных тройников имеют место те же соотношения между стволом и ветвями, что и для транспортных:

[k(b)H₁(b)]^3/2 + [k(b)H₂(b)]^3/2 = 1, (3.15)

W_М1(b)/W_X₁(b) = W_M₂(b)/W_X₂(b) = W_MC(b)/W_XC(b) = 0,5. (3.16)

Очевидно, что в пределах гипертензии от покоя до максимальной физической нагрузки во всех обменных тройниках отношения архитектонических и энергетических «противоположностей» неизменны. Эти отношения аналогичны таковым для транспортных тройников [196]. Полная аналогия указывает на то, что как на транспортном, так и на обменном участке, энергооптимальные отношения «противоположностей» в сосудах тройников независимо от уровня гипертензии аналогичны. Установленные инварианты (3.15) и (3.16) универсальны и являются общими для всех тройников докапиллярного русла. Таким образом, очевидна гармония оптимального вхождения «противоположностей» архитектонических, гемодинамических и биохимических параметров в систему «Обменный тройник» при любой гипертензии. Следует в связи с этим вспомнить предвидение выдающегося ученого 20 столетия А.Л. Чижевского (1897-1964): «Кровяное русло должно быть в высокой степени упорядочено геометрически, физически и химически» [208, с. 13].

3.4.3. Протяженность, поверхность обменного участка

и гармония «противоположностей»

Газообмен крови с окружающими тканями - важнейшая функция микрососудистого русла. Поэтому необходимо рассмотреть основные параметры, связанные с этой функцией, - протяженность и поверхность обменного участка и время пребывания эритроцитов в обменных сосудах. Докапиллярный участок сердца представляет собою своего рода пирамиду, на вершине которой находится первая от аорты коронарная артерия, а в основании - генерации прекапиллярных тройников. На микрососудистый участок приходятся сосуды с диаметром от d_max » 100 мкм до d_min » 7 мкм. Микрососудистые генерации составляют более 90% от общей длины и боковой поверхности всего гемоартериального участка. Отметим важную деталь: генерации всех тройников на микрососудистом участке практически симметричны [49]. Микроучасток можно условно разделить на две части: 1) «стандартную» (С=l/d=3), где d₁(b_ЗС) = d₂(b_ЗС)=0,794d_С(b_ЗС) и l₁(b_ЗС) = l₂(b_ЗС)=0,794l_С(b_ЗС) и 2) «нестандартную» (С=l/d>3), где d₁(b_ЗС) = d₂(b_ЗС)=0,794d_С(b_ЗС) и l₁(b_ЗС) = l₂(b_ЗС)>0,794l_С(b_ЗС). Относительные изменения диаметров ветвей как в «стандартных», так и «нестандартных» тройниках соответствуют принципу «минимальной» работы [216]. Однако в «нестандартных» тройниках относительные изменения длин ветвей превышают «стандартные» и тем в большей степени, чем ближе эти тройники к капиллярам. «Стандартная» часть микроучастка включает в себя сосуды в диапазоне d » 40 ÷ 100 мкм. Отдельный эритроцит на этом участке отдает столь незначительное количество кислорода, что «кислородным» вкладом этого участка в дальнейшем при расчетах можно пренебречь. «Нестандартный», обменный участок составляют сосуды в диапазоне d»7÷40 мкм; этот участок включает 8 докапиллярных генераций [203]; из этих сосудов происходит диффузия кислорода в ткани.

Определим, сколько энергооптимальных ветвлений N приходится на цепочку микрососудов,

N = [lnd_max(b_ЗС) – lnd_min(b_ЗС)]/ln1,26 » 12,

где d_max(b_ЗС) = 100 мкм , d_min(b_ЗС) = 7 мкм в золотом режиме гипертензии. Из этого выражения следует, что количество ветвлений зависит только от начального и конечного диаметров, но не зависит от длины сосудов. Следует отметить при этом, что количество сосудов, которое проходит отдельный эритроцит на микроучастке, одинаково для всех млекопитающих. На «стандартной» части у всех микрососудов коэффициент конструкции примерно одинаков (C=l/d»3). Однако в «нестандартных» сосудах по мере снижения диаметра коэффициент их конструкции, напротив, возрастает (C>3) [216, 203]. Представим соотношение длины ветвей и ствола «нестандартного» тройника следующим образом: l₁(b_ЗС) = l₂(b_ЗС) = 0,794k_Ll_C(b_ЗС). В этом произведении величина 0,794 представляет «стандартное» изменение длины ветвей (С=3), коэффициент k_L отражает дополнительное удлинение «нестандартных» ветвей по отношению к их «стандартной» величине. Величина k_L = C₁/C_C = C₂/C_C, где C_C, C₁, C₂ – коэффициенты конструкции ствола и ветвей. Очевидно, что для всех «стандартных» тройников k_L»1. Напротив, величина k_L по мере уменьшения калибра «нестандартных» сосудов возрастает (k_L>1).

Рассмотрим связь между диаметром микрососудов и вязкостью крови. В «стандартном» диапазоне d=40-100 мкм уменьшение диаметра ветвей по отношению к стволу в 0,794 раз не вызывает значительного изменения вязкости крови (см. рис. 3.6). Вязкость крови в стволе и ветвях «стандартных» тройников практически одинакова: x₁(b_ЗС)= x₂(b_ЗС) = x_C(b_ЗС). В «нестандартных» тройниках вязкость крови: x₁(b_ЗС) = x₂(b_ЗС) = k_xx_C(b_ЗС), где k_x= x₁(b_ЗС)/x_С(b_ЗС) = x₂(b_ЗС)/x_С(b_ЗС). Величина k_x по мере уменьшения диаметра снижается (k_x <1) (см. рис. 3.6). Таким образом, в «стандартных» тройниках коэффициент k_x»1, в «нестандартных» тройниках k_x<1. С учетом коэффициентов k_L и k_x давление DP(b_ЗС) в ветвях любого симметричного тройника по отношению к стволу

DP₁(b_ЗС) = DP₂(b_ЗС) = 128Q_C(b_ЗС)[k_Ll_C(b_ЗС)k_xx_C(b_ЗС)]/pd_C(b_ЗС)⁴, (3.16а)

где Q_C(b_ЗС), d_C(b_ЗС), l_C(b_ЗС), x_C(b_ЗС) – соответственно кровоток, диаметр и длина ствола, вязкость крови в стволе в золотом режиме гипертензии. Очевидно, в «стандартных» тройниках произведение k_Lk_x»1. Однако, и в «нестандартных» тройниках произведение k_Lk_x»1, поскольку «обратные» относительные изменения k_L и k_x «компенсируют» друг друга [203]. Вследствие того, что для любого микрососуда k_Lk_x»1, давление на стволе и ветвях всех «стандартных» и «нестандартных» тройников будет одинаковым: DP₁(b_ЗС) = DP₂(b_ЗС) = DP_C(b_ЗС). Как мы уже отмечали выше, в 8 прекапиллярных генерациях имеет место «нестандартное» отношение C=l/d>3. Согласно данным К.А. Шошенко [216], в первых двух обменных генерациях, начиная от капилляров, каждый из сосудов имеет удвоенную длину по отношению к «стандартной» в сосуде того же калибра (C=l/d=6, k_L=2). Длина каждого из сосудов трех последующих генераций (l/d=5, k_L=1,67) равна увеличенному в 1,67 раз «стандартному» размеру. Всякий сосуд из трех следующих генераций (l/d=4, k_L=1,33) имеет длину, увеличенную в 1,33 раз по отношению к «стандартной» величине. При дальнейшем отдалении генераций от капилляров обменные микрососуды становятся «стандартными» (l/d=3, k_L=1). Давление на всех «стандартных» и «нестандартных» сосудах, как было показано выше, одинаково. Несложно показать, что «нестандартное» сопротивление каждого сосуда также равно его «стандартному» аналогу, поскольку k_Lk_x»1. Вследствие этого, кровоток в каждом «нестандартном» сосуде равен его «стандартной» величине. Однако при этом существует различие: за счет «нестандартного» удлинения объем «нестандартного» сосуда по отношению к его «стандартной» величине возрастает в k_L раз. Вследствие этого, очевидно, что время пребывания эритроцита в каждом «нестандартном» сосуде по отношению «стандартному» того же калибра также увеличивается в k_L раз (см. Табл. 4).

Какую роль в прозведении k_Lk_x играют сомножители k_L и k_x и что произойдет, если их изменять по отношению к естественным величинам? Отметим, что в соответствии с выражением (3.1) величина k_x на протяжении «нестандартного» участка «привязана» к оптимальным диаметрам микрососудов (см. рис. 3.6). Как следствие, коэффициент k_x определяется реологическими свойствами крови в соседних сосудах; поэтому величина k_x в произведении зафиксирована. Коэффициент k_L от диаметра не зависит. При анализе значения k_Lk_x следует рассмотреть изменения этого произведения в пределах: k_Lk_x£1 или, наоборот, k_Lk_x<1. Рассмотрим вначале «естественную» ситуацию, когда k_Lk_x=1. Предварительно отметим, что на обменном участке имеет место значительная дополнительная отдача кислорода за счет «нестандартного» удлинения сосудов [203]. Если бы все «нестандартные» сосуды были бы «заменены» на «стандартные», то общее время пребывания эритроцита на обменном участке было бы в 8 раз больше, чем в одном «стандартном» сосуде. Однако несложно показать, что в «нестандартных» сосудах общее время возрастает в 13 раз [203]. Очевидно, что общее время пребывания эритроцита в обменных «нестандартных» сосудах возрастает в 1,62 (золотое число!) раз. Таким образом, имеет место золотая гармония «противоположностей» между общим временем пребывания эритроцита в «нестандартных» и «стандартных» обменных микрососудах. Этот феномен имеет, как мы увидим дальше, большое «кислородное» значение.

Пока же сравним два варианта последовательного расположения микрососудов на обменной цепочке (d=7¸40 мкм): возможный («стандартный») и естественный («нестандартный»). Как будет нами показано в разделе 3.6, чем меньше диаметр сосуда, тем больше кислорода отдает в нем отдельный эритроцит за единицу времени. Эритроцит пребывает в любом «нестандартном» сосуде большее время, чем в «стандартном» того же калибра. Поэтому количество кислорода, отдаваемого в любом «нестандартном» сосуде, всегда больше, чем это было бы в «одноименном» «стандартном». Чем ближе «нестандартный» сосуд к капилляру, тем больше «добавка» времени пребывания и тем большее количество кислорода дополнительно отдает эритроцит за время прохождения сосуда. Поскольку «естественное» произведение ξl»1, очевидно, что не только давление, но и проводимость и кровоток в любом «нестандартном» сосуде равны их величинам в «стандартном» сосуде того же калибра. Как следствие, можно говорить об одинаковой затрате энергии и в «стандартных», и «нестандартных» генерациях сосудов одинакового диаметра! Все «нестандартные» генерации потребляют столько же энергии, сколько потребляло бы аналогичное количество их «стандартных» аналогов. Но при этом следует обратить внимание на важный «выигрыш». За счет дополнительного, «нестандартного», удлинения обменные сосуды отдают дополнительный объем кислорода без дополнительных затрат энергии на перемещение крови! Отметим еще одно важное обстоятельство: наибольшее отклонение от «стандартного» варианта по времени приходится на самые близкие к капиллярам «нестандартные» генерации, где отдача кислорода наиболее эффективна.

Рассмотрим, каким образом влияет величина k_L на кислородное обеспечение клеток сердца, когда k_Lk_x>1 или, наоборот, k_Lk_x<1? Предварительно примем плотность капиллярной сети миокарда равной естественной при любой величине k_Lk_x, а количество сосудов в обменной цепочке постоянным. Кислород, поступающий из капилляров в клетки, имеет два показателя: «количество» и «качество». Обеспечение по «количеству» соответствует вхождению в клетки адекватного объема кислорода, «качество» же обозначает адекватную величину рО₂ в молекулах поступающего кислорода. Рассмотрим вариант, когда во всех сосудах произведение k_Lk_x>1. В этом варианте эритроцит будет отдавать кислород в каждом обменном сосуде дольше, чем в естественном варианте. Естественно, при этом величина рО₂ на входе капилляров, а, следовательно, и в клетках становится ниже естественной, оптимальной величины; при этом клетки получают кислород «низкого качества». При k_Lk_x<1 время пребывания эритроцитов в сосудах по отношению к естественному варианту, наоборот, уменьшается. При этом величина рО₂ в капиллярах и клетках возрастает выше их естественных значений; при этом скорость дыхания митохондрий в клетках будет ниже оптимальной. Таким образом, в естественном варианте, когда k_Lk_x=1 в каждом сосуде, скорость дыхания митохондрий в сердечных клетках равна оптимальной (см. раздел 4.9), что обеспечивает наиболее эффективную жизнедеятельность дыхательной системы клетки. Показано [203], что при естественном варианте имеет место оптимальное кислородное обеспечение кардиомиоцитов как по «количеству», так и по «качеству». В этом варианте имеет место и наибольший объем кислорода, поступающий в клетки из обменных сосудов за единицу времени, и максимальная скорость дыхания в кардиомиоцитах. (В отношении аспектов кислородного обеспечения клеток по «количеству» и «качеству» можно провести аналогию с теплом, поступающим в комнату от нагревателя. «Количество» - это калории тепла, поступающие в единичный объем помещения за единицу времени, а «качество» - температура воздуха в единичном объеме) При оптимальном сопряжении «противоположностей» кислородных параметров, характеризующих «количество» и «качество», обеспечивается оптимальная деятельность энергетической системы кардиомиоцита (см. раздел 4.9). Длина и вязкость в «нестандартных» сосудах «подобраны» Природой таким образом, чтобы обеспечить оптимальное функционирование дыхательной системы кардиомиоцитов. Очевидно, что только при естественной величине произведения k_Lk_x=1 возможно оптимальное кислородное обеспечение кардиомиоцитов и по «количеству», и по «качеству». На основании вышеизложенного можно сделать вывод: естественной величине k_Lk_x=1 соответствует оптимальное сопряжение кислородных «противоположностей» в клетках миокарда. Добавим к этому, произведение k_Lk_x=1 остается неизменным при любом уровне гипертензии, поскольку на микроучастке размеры сосудов и вязкость крови остаются аналогичными их величинам в золотом режиме.

Очевидно, что количество домикрососудистых генераций сердца у различных видов млекопитающих будет различным. Однако количество микрососудистых генераций у всех животных, несмотря на различие в размерах, одинаково. Конечной «целью» естественной конструкции домикрососудистого участка является создание условий для синхронного движения эритроцитов по «одноименным» генерациям обменных микрососудов и в дальнейшем по капиллярам. Величина диаметра капилляра и его длина имеет важнейшее значение. Отметим, количество кислорода, поступающее в кардиомиоциты из капилляров, составляет более 80% от всего объема потребляемого кислорода. Обратимся к кривой x=f(d) (см. рис. 3.6). Максимальное отношение поверхности сосуда к его объему (S/V) на обменном участке соответствует диаметру капилляра (d_k=5÷6 мкм). При дальнейшем уменьшении диаметра эритроциты разрушаются [242], а вязкость крови резко возрастает. Таким образом, «выбор» диаметра капилляра обеспечивает для всех звеньев обменного участка: 1) минимально возможную вязкость крови и 2) максимально возможное соотношение S/V. «Выбор» минимально возможного диаметра капилляра позволяет все обменные микрососуды полностью расположить на наиболее «выгодном», наклонном, участке кривой вязкости крови x=f(d) (см. рис. 3.6). При этом обеспечиваются: 1) минимальные потери энергии на перемещение единичного объема эритроцитов и 2) максимально возможный уровень обмена между кровью и кардиомиоцитами. Таким образом, мы могли убедиться, что на кривой x=f(d) Природа выбрала ряд «рабочих» точек, где каждой точке помимо вязкости соответствует «свое» оптимальное соотношение l/d; эти соотношения остаются практически неизменными при любом уровне гипертензии.

Отметим, что смещение «рабочей» величины диаметра капилляра по кривой x=f(d) вправо означало бы уменьшение числа генераций, отдающих кислород. Вследствие этого уменьшился бы объем и возросла энергетическая «стоимость» отдаваемого кислорода. Кроме того, снизился бы уровень газообмена между кровью и сердечной тканью. С другой стороны, снижение диаметра капилляров ниже 5 мкм привело бы к разрушению эритроцитов и резкому росту вязкости крови. Оптимальное положение капилляров и микрососудов на кривой x=f(d) и соответствующие им величины x и l/d обеспечивают оптимизацию адекватного кислородного обеспечения миокарда как по «количеству», так и по «качеству». На всякой генерации микрососудов происходит создание оптимальных «количественных» и «качественных» кислородных величин, каждая из которых является оптимизацией своих «противоположностей».

Заключение. Представленные особенности архитектоники сосудов и реологических свойств крови на обменном участке обеспечивают оптимальное кислородное снабжение сердечных тканей по «количеству» и «качеству». Этот феномен имеет в своей основе оптимальное сопряжение «противоположностей» всех рассматриваемых параметров.

3.5. Фракталы, докапиллярное «дерево» и кардиограммы

Учение о фракталах является одним из методологических инструментов, позволяющих вскрыть основу организации многих живых систем. Основоположник фрактальной геометрии Б. Мандельброт назвал фракталами структуры, обладающими двумя важнейшими признаками: изломанностью и самоподобием [116]. Фрактальным множествам присуща масштабная инвариантность (самоподобие) их внутренней структуры: любая малая часть фрактала воспроизводит всю его структуру. Широчайшая распространенность фрактальных структур в природе объясняется их разномаштабностью и самоподобием: и большие, и малые элементы фрактальных структур имеют одинаковый закон построения. Например, законы ветвления самой тонкой веточки дерева абсолютно те же самые, что и для всех его ветвей – больших и малых – и для всего ствола в целом. Отметим, что ряды «золотых» чисел и чисел Фибоначчи также обладают свойством самоподобия. Отметим в частности, последовательности золотых чисел и чисел Фибоначчи в сердечных системах в своей основе также родственны фракталам (см. разделы 2.2 и 2.3). Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии. Многие объекты живой природы имеют ярко выраженную фрактальную структуру (деревья, кровеносные сосуды, нейронные сети и др.). Проявление общей биоэнергетической направленности структур и функций живых систем обнаружено на всех уровнях организации живой природы: от макромолекулярного до биосферного, что сродни проявлению свойства самоподобия объектов, отображаемых фрактальными зависимостями [40].

Рассмотрим некоторые зависимости самоподобия на примере архитектоники сердца и кардиограмм.

Докапиллярное «дерево». Фрактальный принцип наглядно представлен в последовательном разветвлении артериальныхсосудов. Докапиллярное «дерево» сердца, включающее в себя транспортные и обменные сосуды, имеет конструкцию, близкую к фрактальной (см. рис. 3.5). Самоподобие конструкции «дерева» заключается, прежде всего, в том, что все ветвления сосудов представлены бифуркациями. Структурной единицей фрактального «дерева» сердца является сосудистый тройник, объединяющий ствол и две ветви. Идеальное самоподобие всех тройников имеет место тогда, когда существует: 1) полная симмметрия ветвлений (d₁=d₂=0,794d_C) и 2) равенство коэффициентов конструкции (l₁/d₁=l₂/d₂=l_C/d_C) по всему протяжению «дерева». Однако, реально сердечных тройников, полностью удовлетворящих условиям 1) и 2), практически не существует. Эта особенность соответствует определению фрактала, представленного Мандельбротом: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». На основе проведенного нами анализа нельзя говорить о полном самоподобии сердечных тройников. Этот вывод следует из анализа ветвления сердечных сосудов. На транспортном участке ветвления имеют асимметричную форму, но при этом коэффициент конструкции сосудов приблизительно постоянен. Асимметрия ветвления транспортных сосудов по мере уменьшения их калибра постепенно приближается к симметрии. На микрососудистом участке имеет место симметричное ветвление, но по мере уменьшения диаметра микрососудов происходит рост коэффициента конструкции. Кроме того, углы разветвления тройников неодинаковы. Исходя из этих особенностей, не представляется возможным говорить о полном самоподобии элементов «дерева». Однако общими для всего «дерева» являются бифуркационное ветвление и оптимальность диаметров всех сосудов, их энергооптимальное соединение в тройники. Как было показано выше, такая конструкция артериальной и микрососудистой частей «дерева» позволяет обеспечивать кислородное снабжение сердца с минимальными затратами энергии и сосудистого вещества. Отметим, что элементы фрактальности присутствуют и в других конструкциях сердца. Известно [77], что митральный и трехстворчатый клапаны к мышцам прикрепляют ветвящиеся сухожилия. Фрактальная организация прослеживается так же и в разветвлении некоторых сердечных мышечных волокон и в системе Гиса, передающей электрические сигналы от предсердий к желудочкам. Естественно предположить, что форма этих фрактальных структур соответствует минимальному расходу энергии и вещества.

Кардиограммы сердца. Был выполнен анализ кривых сердечного ритма здоровых людей в различных временных интервалах [77]. На кривых, соответствующих нескольким часам, одному часу и нескольким минутам флуктуации выглядели подобными самим себе так же, как и ветки геометрического фрактала. Таким образом, было установлено, что признаком здоровья является не стабильный сердечный ритм, а повторяющиеся в разных масштабах «скачки» амплитуды сердечных сокращений.

3.6. Кислородные параметры обменных микрососудов в золотом режиме гипертензии

Оптимальное сопряжение на обменном участке параметров архитектоники, гемодинамики и кислородного обеспечения имеет важнейшее значение для адекватного снабжения кислородом сердечных клеток по «качеству» и «количеству». К аспекту «качества» кислорода следует отнести разность его напряжений на концах обменной артериолы, аспектом «количества» является объем кислорода, исходящий из микрососуда за единицу времени. Установлено [68, 247], что кислород начинает поступать в ткани из прекапиллярных артериол. Наибольшее значение имеют генерации артериол с диаметром менее 40 мкм; из них в сердечную ткань поступает почти 12% от общего количества кислорода. «Вклад» сосудов с d>40мкм в снабжение тканей незначителен. Для «кислородного» анализа нами выбрана цепочка из 10 обменных микрососудов вплоть до капилляра, двигаясь по которой эритроцит отдает кислород в окружающие ткани (см. рис. 3.7). Обозначим диаметры сосудов, начиная от капилляра и далее по направлению к аорте: m=1, 2,…10. Диаметры в этом направлении изменяются следующим

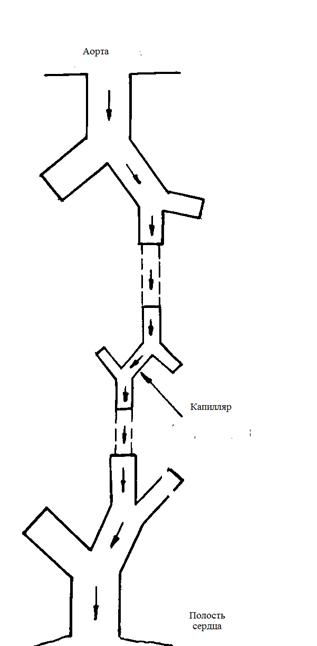
Рис. 3.7. Цепочка сердечных сосудов от аорты до капилляра, по которой движется отдельный эритроцит

образом:

d_m₊₁(b_ЗС) = d_m(b_ЗС)/, (3.17)

где d_m(b_ЗС), d_m+1(b_ЗС) - диаметры m- и m+1-сосудов цепочки, начиная от капилляра, в золотом режиме гипертензии. Рассмотрим «работу» обменной цепочки в сердце собаки. Диаметр сердечного капилляра собак d_K(b_ЗС)=5,5 мкм [233]; эта величина для различных видов млекопитающих практически одинакова [78] Расчетные значения диаметров первых 10 звеньев приведены в Табл. 4.

Время пребывания эритроцитов в терминальных сосудах можно определить по формуле [203]:

t_m₊₁(b_ЗС) = [С_m₊₁(b_ЗС)/С_m(b_ЗС)]t_m(b_ЗС). (3.18)

Продолжительность прохождения эритроцита через артериальный участок сосудистого тракта составляет (15-20)% от общего времени [169]. В покое общее время пребывания эритроцита в коронарном русле собак при нормальном среднем давлении в аорте составляет 4 с [236]. По нашим расчетам количество артериальных генераций в сердце собак N=28 [203]. Примем время движения эритроцитов по артериальному руслу от аорты до капилляра равным 600 мсек (15% от общего времени). Выражение (3.18) справедливо для любых двух соседних звеньев цепочки с d<40 мкм, по которой движется отдельный эритроцит. Для сосудов с d> 40 мкм коэффициент конструкции «стандартный»: C_m(b_ЗС)=3 (см. Табл. 4, столбец 3). При приближении терминальных артериол к капилляру отношение С_m₊₁(b_ЗС)/С_m(b_ЗС), как нам уже известно, последовательно возрастает в пределах 1,33¸2. В соответствии с представленными величинами время пребывания в каждом «стандартном» сосуде t_m(b_ЗС)=18,5 мcек. Количество генераций на обменном участке у всех млекопитающих практически одинаково, поскольку у всех животных диаметр обменных микрососудов изменяется в пределах от 40 до 7 мкм.

Исходя из представленных величин, рассчитаем время пребывания эритроцитов в 10 терминальных артериолах сердца млекопитающих (см. Табл. 4, столбец 4). В соответствии с параметрами, известными ранее и вычисленными по (3.17) и (3.18), в первом от капилляра сосуде (m=1) ΔP₁(b_ЗС)=3,5 мм рт. ст., t₁(b_ЗС)=0,037 c, ξ₁(b_ЗС)=1,45×10^-2 Пз, d₁(b_ЗС)=6,9×10^{-4 см. С учетом этих величин нами получены значения
для других параметров:}q₁(b_ЗС)=41,9×10^{-9 см3}×с^-1, V₁(b_ЗС)=1,53×10^-9 см³, G₁(b_ЗС) = 0,91×10^-11 г^-1×см⁵×с^-1. Используя эти величины и С₁(b_ЗС)=6 в качестве исходных, можно вычислить значения аналогичных параметров для других обменных звеньев цепочки.

Табл. 4. Величины конструктивных и кислородных параметров в терминальных артериолах сердца [203]

m	d_m(b_ЗС), мкм	С_m	t_m(b_ЗС), мсек	U_m(b_ЗС), %/сек	DHbO₂_m(b_ЗС), %	DpO_2m(b_ЗС), мм рт. ст.
1	6,9	6	37,0	138,3	5,04	11,0
2	8,7	6	37,0	87,0	3,10	10,1
3	11,0	5	30,9	54,7	1,66	6,9
4	13,9	5	30,9	34,4	1,05	4,9
5	17,5	5	30,9	21,6	0,667	4,0
6	22	4	24,6	13,6	0,30	3,5
7	27,8	4	24,6	8,5	0,14	2,4
8	35,0	4	24,6	5,3	0,080	1,1
9	44,0	3	18,5	-	-	-
10	55,6	3	18,5	-	-	-

Примечания: m - номер обменного сосуда цепочки по направлению капилляр – аорта; t_m(b_ЗС) - время пребывания эритроцита в m-сосуде, U_m(b_ЗС) - скорость отдачи кислорода отдельным эритроцитом в поперечном сечении m-сосуда, DHbO_2m(b_ЗС) - количество кислорода, отданного отдельным эритроцитом за время пребывания в m-сосуде, DрО_2m(b_ЗС) – разность напряжений кислорода на концах m-сосуда в золотом режиме гипертензии.

Перейдем к непосредственному расчету кислородных параметров. Каждый эритроцит отдает кислород, перемещаясь по цепочке обменных артериол, включая капилляр. Следует заметить, что между капилляром и терминальными артериолами много общего. Стенки мельчайших артериол и капилляров имеют весьма сходное строение: эпителий, тончайшая базальная мембрана и сравнительно редкие и очень тонкие пучки гладких мышц. Все эти образования имеют такой же коэффициент диффузии для О₂ и СО₂, как и окружающие ткани. Эритроциты при перемещении в артериолах с диаметром менее 40 мкм так же, как и в капиллярах, принимают парашютообразную форму [292]. По расчетам Федершпиля и Попеля [252] эритроциты отдают кислород с одинаковой скоростью независимо от степени их отклонения от продольной оси сосуда. Экспериментально установлено [323], что количество кислорода, поступающее в ткани через единицу поверхности артериолы за единицу времени, не меняется при значительном изменении кровотока, величины гематокрита и степени насыщения кислородом движущейся крови. Другими словами, за единицу времени микрососуд всегда отдает постоянное количество кислорода независимо от представленных изменений в протекающей крови. Скорость отдачи кислорода обусловлена только величиной потребления кислорода окружающей тканью, а она по всей длине цепочки микрососудов, включая капилляр, одинакова. Следовательно, общее количество кислорода, поступающее за единицу времени из каждого поперечного сечения сосудов любого калибра, всегда одинаково. Естественно, «вклад» отдельного эритроцита в общую диффузию будет тем больше, чем меньше поперечная площадь сосуда. В капилляре отдельный эритроцит отдает кислород с максимальной скоростью. Очевидно, что соотношение скоростей отдачи кислорода отдельным эритроцитом в двух соседних микрососудах обратно пропорционально соотношению их поперечных площадей. Исходя из этих рассуждений, в m-сосуде по отношению к капилляру:

U_m(b_ЗС) =U_K(b_ЗС)S_K(b_ЗС)/S_m(b_ЗС), (3.19)

где U_m(b_ЗС), U_K(b_ЗС), S_m(b_ЗС), S_K(b_ЗС) - соответственно скорость отдачи кислорода отдельным эритроцитом и площадь поперечного сечения в m-артериоле и капилляре в золотом режиме гипертензии.

Установлено [37, 38], что напряжение кислорода на артериальном конце капилляров в тканях составляет 40-60 мм рт. ст. Примем для дальнейших расчетов в исходном режиме рО₂(b_ЗС)=50 мм рт. ст., а в первой коронарной артерии рО₂=95 мм рт. ст. На кривой диссоциации гемоглобина человека (см. рис. 3.8), взятой нами из книги Уайт и др. [176], этому интервалу соответствует разность насыщения кислородом ΔHbO₂=12%. Показано [255], что в миокарде величины рО₂ в крупных, средних и мелких артериях точно следуют величине рO₂ в аорте. Диффузия кислорода начинается в артериолах диаметром менее 100 мкм. В микрососудах с диаметром более 40 мкм отдача кислорода отдельным эритроцитом очень мала и этой величиной при расчетах в дальнейшем можно пренебречь. При прохождении m-сосуда разность насыщения кислородом эритроцита кислородом в этом сосуде:

ΔHbO₂(b_ЗС) = U_K(b_ЗС)t_m(b_ЗС)[S_K(b_ЗС)/S_m(b_ЗС)].

Рис. 3.8. Кривая насыщения гемоглобина человека [176]. По оси абсцисс – рО₂ в мм рт. ст.; по оси ординат - HbO₂ в %. Точки A, B, C, D – границы логарифмического участка кривой (см. рис. 16). Интервал CD - pO₂=19-65 мм рт. ст. интервал AB – HbO₂=28,7-91,8%; точкам M и N соответствуют рО₂=50 мм рт ст. и HbO₂=85% на артериальном конце капилляра в золотом режиме гипертензии.

Для расчетов используем первые 8 генераций обменных сосудов (см. Табл. 4, столбец 6); при m>8 расчетные значения U_m(b_ЗС) изменяются незначительно. Общий «разряд» эритроцита на 8 звеньях цепочки:

ΔHbO₂(b_ЗС) = U_K(b_ЗС)S_K(b_ЗС)(b_ЗС)/S_m(b_ЗС). (3.20)

Скорость отдачи кислорода эритроцитом в капилляре в золотом в режиме можно определить по формуле:

U_K(b_ЗС) = [ΔHbO₂(b_ЗС)/S_K(b_ЗС)]/ (b_ЗС)/S_m(b_ЗС). (3.21)

Приняв ΔHbO₂(b_ЗС)=12%, S_k(b_ЗС)=23,7×10^-8 см² и используя значения d_m(b_ЗС) и t_m(b_ЗС), приведенные в табл. 4, можно вычислить величину U_K(b_ЗС), а также U_m(b_ЗС) и ΔHbO_2m(b_ЗС); последние приведены в табл. 4 (см. столбцы 5 и 6). Расчетная величина скорости отдачи кислорода U_K(b_ЗС)=215%/с незначительно отличается от максимальной – 220 %/с. Эта величина была рассчитана и экспериментально установлена для движущихся эритроцитов в плазме с имитацией потребления кислорода [301, 211]. Наши расчеты подтверждают, что «в живых организмах скорость химических реакций всегда достигает предельного значения, которое определяется законами физики» [220, с. 96]. Для дальнейших расчетов будем использовать величину U_K(b_ЗС)=220 %/с. В артериолах с диаметром менее 40 мкм скорость отдачи кислорода единичным эритроцитом быстро возрастает; растет и время пребывания эритроцитов в сосуде. Отметим, что экспериментально установлено [68, 70], что в артериолах мозга и мышц особо резкое падение рО₂ происходит в сосудах диаметром 10-15 мкм и ниже. Эта экспериментально установленная тенденция совпадает с нашими расчетами (см. Табл. 4, столбец 7).

В покое на артериальном конце сердечного капилляра рО₂(b_ЗС)»50 мм рт. ст. [38, 39], а на венозном рО₂(b_ЗС)=20 мм рт. ст. [321]. Большое значение для равенства рО₂ на артериальных концах капилляров имеет близость прекапиллярных тройников к полной симметрии [49]. Эритроциты в симметричных ветвях терминальных тройников отдают равное количество кислорода и входят в капилляры с приблизительно одинаковыми рО₂, что соответствует одинаковому «качеству» кислорода. В противном случае, если бы вхождение и выход эритроцитов происходило со значительными отклонениями от величин рО₂(b_ЗС)=50 мм рт. ст. и рО₂(b_ЗС)=20 мм рт. ст., было бы нарушено условие одинакового «качества» кислорода, поступающего в сердечные ткани из капилляров.

Рассмотрим «количество» и «качество» кислорода, поступающего из обменных артериол. Как было показано выше, каждое поперечное сечение артериол независимо от их диаметра отдает такое же количество кислорода, что и сечение капилляра. Иными словами, количество кислорода, поступающее за единицу времени из микрососуда известной длины, равно объему кислорода из капилляра той же длины. «Качество» кислорода, поступающего из артериол в клетки, также равно «капиллярному». Это обусловлено тем, что чем больше диаметр сосуда, тем толще его стенка и, следовательно, больше падение величины рО₂ на последней. Вследствие этого величины рО₂ в ткани уже на незначительном удалении от стенки обменных артериол и капилляров приблизительно равны [71]. Представленное сходство условий диффузии кислорода в капиллярах и микрососудах позволяет сделать вывод, что с «кислородной» точки зрения последние ничем не отличаются от капилляров. Добавим к этому, что обменные артериолы, также как и капилляры, параллельны мышечному волокну, которое они обеспечивают кислородом [270, 55]. Таким образом, «кислородная работа» артериол ничем не отличается от капилляров за исключением одного обстоятельства. Разница заключается в «цене» кислорода. Энергетическая «стоимость» единичного объема кислорода, потребляемого из микрососудов, в артериолах выше, чем в капилляре. Эта «цена» тем больше, чем крупнее диаметр обменного микрососуда. Таким образом, с точки зрения дешевизны потребляемого кислорода, имеет место оптимальное сопряжение «противоположностей»: общее количество «дешевых» и общее количество «дорогих» «капилляров». Энергооптимальная гармония этих «противоположностей» обеспечивает оптимальные величины «количества» и «качества» кислорода, поступающего в кардиомиоциты, при минимальных затратах энергии.

Как будет показано в 4 главе (см. рис. 4.3), сегмент кривой диссоциации оксигемоглобина, соответствующий рО₂=19-65 мм рт. ст., обладает особыми, логарифмическими, свойствами. Этими свойствами обусловлено оптимальное сопряжение «по кислороду» прекапиллярной и капиллярной частей обменного коронарного русла. Прекапиллярные сосуды являются своего рода переходной конструкцией, где происходит предварительная организация оптимальных условий для диффузии кислорода на важнейшей части обменного русла - капиллярах. Точка раздела «противоположностей» - «микрососудистой» и «капиллярной частей на кривой HbO₂=f(pO₂) - определяет оптимальное кислородное обеспечение миокарда по «количеству» и «качеству».

Отметим «золотую» особенность распределения скорости отдачи кислорода отдельным эритроцитом по цепочке обменных сосудов. Выше нами показано, что количество кислорода, отдаваемого всеми эритроцитами в каждом поперечном сечении любой артериолы за единицу времени, равно постоянной величине U(b_ЗС)=220%/с. Эта величина не зависит от диаметра микрососудов. Последовательность значений U_m(b_ЗС)= 5,3; 8,5; 13,6; 21,6; 34,4; 54,7; 87,0; 138,3; 220 % с^-1(см. Табл. 4, столбец 5) близка к классическому ряду чисел Фибоначчи: 5, 8, 13, 21, 34, 55, 89, 144, 233. Представленная последовательность указывает на то, что скорость отдачи кислорода единичным эритроцитом в терминальных артериолах и в капилляре изменяется по аналогии с рядом чисел Фибоначчи. Эта аналогия сохраняется при любой гипертензии (см. раздел 4.5). Размеры и архитектоника терминальных микрососудов у различных видов млекопитающих практически одинаковы [76, 216]. Поэтому можно считать, что скорость отдачи кислорода отдельным эритроцитом в «одноименных» прекапиллярных сосудах сердца у млекопитающих (независимо от их размера и веса) одинакова. Скорости «кислородного разряда» эритроцита в последовательности терминальных артериол являются инвариантными оптимальными величинами, соотносящимися между собой по аналогии с рядом чисел Фибоначчи.

3.7. «Цена» транспорта кислорода на докапиллярном участке

Перейдем к оценке затрат энергии на транспорт единичного объема кислорода в режимах гипертензии. Было показано [203], что в условиях гипертензии в любом эластическом или мышечном сосуде сердца:

W_М(b) = b³W_М(b_ЗС), (3.22)

W_Х(b) = b³W_Х(b_ЗС), (3.23)

где W_М(b_ЗС), W_М(b), W_Х(b_ЗС), W_Х(b) – соответственно средняя за сердечный цикл механическая и химическая мощность, расходуемая в сосуде в золотом и других режимах гипертензии. Очевидно, что суммарный расход механической и химической энергии за единицу времени на транспортном участке SW_тр(b) возрастает в b³ раз:

SW_тр(b) = b³SW_тр(b_ЗС). (3.24)

Отметим, при гипертензии механо-биохимическое воздействие на стенку микрососудов не изменяет их размеров; они остаются постоянными. Вследствие этого, при росте давления на сосуде в b раз, кровоток в сосуде возрастает не в b² раз, как в мышечных и эластических сосудах, а только в b раз. Исходя из этих соотношений, суммарный расход энергии на обменном сосуде за единицу времени должен изменяться следующим образом:

SW_обм(b) = b²SW_обм(b_ЗС). (3.25)

Очевидно расхождение между SW_тр(b) и SW_обм(b). Это расхождение можно объяснить различием в регуляции кровотоков на различных участках коронарного русла. Циркуляция крови на транспортном участке регулируется работой мускулатуры крупных, средних и мелких артерий. На микрососудистом участке регуляция происходит за счет включения или выключения особых мышечных сфинктеров. Такие сфинктеры находятся в пре- и посткапиллярах. В каждый момент функционирует только часть обменных артериол и капилляров, а другая остается в резерве (закрытые артериолы и капилляры). Кроме названных сосудов, доказана принадлежность к микроциркуляторному руслу артериоло-венулярных анастомозов, имеющихся во всех органах и представляющих пути укороченного тока артериальной крови в венозное русло, минуя капилляры [85]. Эти анастомозы подразделяются на истинные анастомозы, или шунты (с запирательными устройствами, способными перекрывать ток крови, и без них), и на межартериолы, или полушунты. Вследствие наличия артериоло-венулярных анастомозов терминальный кровоток делится на два пути движения крови: 1) транскапиллярный, служащий для обмена веществ, и 2) внекапиллярный ток крови, необходимый для регуляции гемодинамического равновесия; последний совершается благодаря наличию прямых связей (шунтов) между артериями и венами (артериовенозные анастомозы) и артериолами и венулами (анастомозы). Благодаря внекапиллярному кровотоку при необходимости происходит разгрузка капиллярного русла и ускорение транспорта крови в органе или данной области тела. Это как бы особая форма окольного, коллатерального, кровообращения [93]. Установлено [352], что в покое перфузируется около 50% всех сердечных артериол. Число одновременно перфузируемых кровью капилляров регулируется работой прекапиллярных сфинктеров. Установлена высокая чувствительность этих сфинктеров к вазоактивным веществам и продуктам метаболизма [355]. Работа каждого сфинктера обеспечивает или открытое или полностью закрытое состояние «своего» микрососуда и капилляра [268]. Отметим, что в течение диастолы большая часть обменных сосудов, открытых в систолу, закрывается, «неиспользованная» часть коронарного кровотока проходит через открывшиеся шунты, которые не участвуют в обмене.

При каждой гипертензии b проводимость увеличивается за счет введения в функциональное состояние «своей» части артериол, капилляров и шунтов. Резервные артериолы, капилляры и шунты дополнительно открываются в количестве, необходимом для кислородного обеспечения клеток по «качеству» и «количеству» в соответствии с изменением гипертензии. Проводимость обменной и шунтовой частей при увеличении гипертензии в b раз возрастает в той же степени. В каждой генерации обменных микрососудов и на капиллярном участке при гипертензии за счет подключения дополнительных сосудов происходит увеличение кровотока в b раз; очевидно, соответственно при этом и «шунтовая» часть кровотока должна возрасти в b раз. Вследствие того, что скорость эритроцитов на обменной и «шунтовой» частях микроучастка также возрастает в b раз, суммарный кровоток увеличивается в b² раз. На всем участке, включающем обменные сосуды и шунты, суммарный расход механической и химической энергии за единицу времени SW_обм(b_ЗС) увеличивается в b³ раз:

SW_микр(b) = b³SW_микр(b_ЗС). (3.27)

Таким образом, и на микрососудистом участке рост потребления энергии за единицу времени тот же, что и на транспортном участке.

Показано [193], что суммарное количество кислорода, поступающее в ткани из открытых обменных артериол и капилляров в течение кардиоцикла, при гипертензии приблизительно возрастает в b² раз:

SB(b) @ b²SB(b_ЗС), (3.28)

где SB(b_ЗС), SB(b) – соответственно общее потребление кислорода сердечной мышцей на обменном участке за единицу времени в золотом и других режимах гипертензии.

Исходя из (3.24), (3.27) и (3.28), можно показать, что в условиях гипертензии «цена» доставки единичного объема потребляемого кислорода по всему докапиллярному участку линейно пропорциональна росту гипертензии:

V(b) = SW(b)/SB(b) = bV(b_ЗС).

Каким образом меняется «цена» транспорта единичного объема потребленного кислорода в обменных генерациях микрососудов? Поскольку суммарная скорость диффузии кислорода из любого сечения каждой артериолы одинакова, то объем кислорода, отдаваемого сосудом за единицу времени, линейно зависит только от длины сосуда. Во всех обменных тройниках

B₁(b_ЗС) + B₂(b_ЗС) = 1,588[С_1,2(b_ЗС)/С_С(b_ЗС)]B_С(b_ЗС),

где B_С(b_ЗС), B₁(b_ЗС), B₂(b_ЗС) - соответственно средний за кардиоцикл объем кислорода, отдаваемый стволом, 1 и 2 ветвями тройника в золотом режиме гипертензии. Если бы в обменных тройниках отношение С_1,2(b_ЗС)= С₁(b_ЗС)/С_С(b_ЗС)=С₂(b_ЗС)/С_С(b_ЗС)=1, то суммарная величина потребляемого из ветвей кислорода по отношению к стволу увеличивалась бы в 1,588 раз. Фактически же отношение длины к диаметру в обменных сосудах по направлению к капиллярам возрастает во все большей степени. Если рассматривать генерации микрососудов по мере убывания их диаметра, то очевидна следующая тенденция: в очередной генерации отдаваемый объем кислорода возрастает более чем в 1,588 раз, а расходуемая мощность остается прежней. Таким образом, сердечная мышца получает дополнительное количество кислорода при «стандартной» затрате энергии на перемещение крови. По мере приближения к капиллярам «цена» единичного объема отдаваемого кислорода все более «дешевеет», достигая минимального значения в капилляре. В режимах гипертензии эта тенденция также сохраняется; однако «цена» потребляемого кислорода в каждом сосуде возрастает в b раз [205].

Обобщая «ценовой» анализ транспорта кислорода, можно сделать следующие выводы:

1) самый «дешевый» кислород доставляется в сердечную мышцу в золотом режиме, а самый «дорогой» - в режиме максимальной гипертензии;

2) в каждом режиме наиболее «дешевый» кислород поступает из обменных сосудов минимального, а самый «дорогой» из обменных сосудов наибольшего диаметра;

3) в любом режиме гипертензии общий расход энергии на транспорт единичного объема потребляемого кислорода по докапиллярному участку имеет оптимальную величину, минимально возможную для этого режима.

Увеличение «стоимости» кислорода при росте гипертензии вызвано необходимостью создать в сердечных клетках напряжение кислорода выше величины, летальной для данного уровня гипертензии. Чем больше гипертензия, тем выше должно быть значение рО₂ в сердечных клетках и обменных сосудах (см. раздел 4.5). Природа «пошла» на дополнительный расход энергии, необходимый для устранения летальной ситуации в клетках. Показано [193], что за счет дополнительного расхода энергии обеспечивается прирост рО₂ в сосудах и сердечной ткани на величину:

dpO₂(b) = 42lgb.

С величиной dpO₂(b) связан рост «цены» доставки единичного объема кислорода. Дополнительные затраты энергии обеспечивают новое «качество» и «количество» потребляемого кислорода. В каждом режиме гипертензии происходит «подбор» оптимальных рабочих величин в пределах возможных значений кислородных параметров. Таким образом, любому уровню гипертензии в каждом обменном сосуде соответствует «своя» энергооптимальная гармония кислородных «противоположностей».

Глава 4.

КАПИЛЛЯРНАЯ СЕТЬ, КАРДИОМИОЦИТЫ И ГАРМОНИЯ «ПРОТИВОПОЛОЖНОСТЕЙ»

4.1. Особенности организации капиллярного участка

Сердечная мышца содержит огромное количество капилляров. Капилляры составляют в среднем 7,3% объема миокарда млекопитающих. Количество капилляров в сердечной мышце примерно равно количеству мышечных волокон [270, 85]. Капилляры находятся в тесном контакте с кардиомиоцитами; каждое мышечное волокно находится в окружении 3-4 капилляров. Стенки капилляров состоят из одного слоя плоских эндотелиальных клеток. Их наружная поверхность лежит на базальной мембране, которая образована непрерывным слоем основного вещества, расположенного между эндотелием и окружающими структурными элементами ткани. В составе стенок кровеносных капилляров нет специализированных сократительных элементов типа мышечных, и поэтому капилляры не могут изменять сосудистый просвет, как это имеет место в артериальных сосудах и артерио-венозных анастомозах. Установлено [111], что существует физиологический механизм, позволяющий периодически включать и выключать капилляры, артериолы, венулы и мелкие артерии и вены таким образом, что количество фунционирующих сосудов сохраняется постоянным, если сохраняется постоянным потребление кислорода и другие факторы, определяющие потребность в кровоснабжении. Капиллярное русло миокарда состоит из обменных (d=5-6 мкм) и магистральных капилляров (диаметр до 20 мкм). В магистральных капиллярах кровь движется в 2-3 раза быстрее [93]; эти капилляры имеют больший диаметр и меньшую длину [93]. Магистральные капилляры, соединяющие артериолы и венулы, не являются фиксированными структурами микроциркуляторного русла, а временно возникают на том или ином участке, выполняя роль шлюзов, открывающих путь для прямого перехода артериальной крови в венозный отдел системы. Отметим, магистральные капилляры не участвуют в газообмене. Таким образом, действующее капиллярное русло миокарда можно подразделить на обменные капилляры, в которых осуществляется обмен, и магистральные, исполняющие роль шунтов. Примерно 1/4 всех сосудов микроциркуляторного русла функционирует в качестве шунтов [362]. Отметим, что в сердце в покое перфузируется около 50% от всех артериол диаметром до 50 мкм. Кроме того, в течение кардиоцикла сердечные артериолы могут открываться и закрываться [352]. Очевидна роль шунтов в течение сердечного цикла, поскольку количество «задействованных» обменных артериол и капилляров в систолу и диастолу различно. Ниже в разделе 4.5 нами будет показано, что количество открытых обменных капилляров в систолу в 14,5 раз превышает их число в диастоле. Кровь, не «задействованная» во время диастолы в обменных микрососудах, проходит через шунты.

Для деятельности капиллярной сети определяющими аспектами являются и гемодинамика, и газообмен, поскольку капилляр одновременно является звеном двух «цепочек» сосудов: «гемодинамической» и «диффузионной». Первая представляет последовательность микрососудов, включая капилляр, двигаясь по которой отдельный эритроцит доставляет кислород к месту потребления. Капилляр является также звеном цепочки последовательно соединенных капилляров; эта цепочка параллельна мышечному волокну. Таким образом, в каждом капилляре представлено пересечение двух цепочек: «гемодинамической» и «диффузионной». Анализ первой цепочки позволяет установить особенности гемодинамического и «кислородного» сопряжения капилляра и прекапиллярных артериол. Выявление количественных взаимосвязей во второй цепочке открывает возможность показать особенности «кислородного» сопряжения сердечных капилляров и мышечного волокна. Ниже будет показано оптимальное сопряжение гемодинамических, кислородных и пространственных параметров на уровне капиллярной системы сердца млекопитающих.

Капилляры представляют собой самую существенную часть микрососудистого русла сердца. Именно из капилляров в ткани поступает основная часть потребляемого кислорода (более 80%). Кислородное обеспечение сердечной ткани зависит от следующих факторов:

1) плотности капиллярной сети;

2) величины коэффициента диффузии и коэффициента растворимости кислорода в сердечной ткани;

3) скорости движения эритроцитов в капиллярах;

4) напряжения кислорода в притекающей к капиллярам крови;

5) скорости дезоксигенации оксигемоглобина в капиллярах;

6) сегмента кривой дезоксигенации гемоглобина, соответствующего «разряду» эритроцита в капилляре.

Организация капиллярного русла сердца млекопитающих в настоящее время достаточно хорошо изучена. Несмотря на значительные различия в плотности васкуляризации отдельных регионов сердца, организация гемокапиллярного русла имеет черты, общие для всего объема миокарда. Общность заключается в следующем:

1. Кровь в капиллярах является неньютоновской жидкостью.

2. Движение крови в капиллярах имеет вращательно-поступательный характер [95, 43].

3. В сердечной мышце капилляры вытянуты по ходу мышечных волокон и приблизительно параллельны друг другу [55, 337].

4. В сердечной мышце имеет место асимметричное расположение капилляров, при котором артериальные и венозные концы соседних капилляров смещены относительно друг друга [250, 337].

5. Размеры капилляров неизменны по всему объему сердца [339].

6. Независимо от степени механического сжатия диаметр, длина, площадь и конфигурация внутренней поверхности капилляров остаются неизменными [336].

7. Плотность капиллярной сети в сердечной мышце тем больше, чем меньше вес животного [312].

8. Диаметр и длина сердечных капилляров одинаковы для различных видов млекопитающих [78].

9. В случае возрастания активности сердца количество открытых капилляров увеличивается [269, 231].

На входе микрососудистой системы еще присутствует небольшая пульсация давления. На уровне артериол пульсация очень сильно снижается, а в капиллярах практически отсутствует. Эффективное гашение пульсовой волны обеспечивается в значительной степени за счет жестких стенок микрососудов и капилляров. Сглаживание пульсовых колебаний обеспечивает постоянство параметров архитектоники и гемодинамики в течение кардиоцикла. Таким образом, отпадает необходимость раздельного анализа параметров в течение систолы и диастолы. В дальнейшем при анализе нами будут использоваться значения параметров, усредненные за сердечный цикл.

4.2. Артериолярно-капилярные тройники

4.2.1. Артериолярно-капилярные тройники в золотом режиме гипертензии

Особый интерес представляют тройники на стыке между последними прекапиллярными артериолами и капиллярами. В этих тройниках стволом является прекапиллярная артериола, ветвями - капилляры. В артериолярно-капилярных тройниках имеет место симметричное ветвление. В соответствии с критерием «минимальной работы»: d_K(b_ЗС)=0,794d_С(b_ЗС). Это соотношение аналогично соотношению диаметров ветвей и ствола в обменных тройниках. Однако коэффициент конструкции капилляра во много раз превосходит таковой для ствола (С=l/d≈40); вследствие этого, l_K(b_ЗС)>>0,794l_С(b_ЗС). «Нестандартное» удлинение капилляра, как будет показано дальше (см. раздел 4.4), имеет большое значение для «удешевления» «цены» потребляемого кислорода.

Естественно возникает вопрос: соблюдаются ли на входе капилляров условия, необходимые для оптимального движения эритроцитов и избежания отеков тканей? Исходя из значений b_K(b_ЗС)=19300 эрг см³ с^-1 [295] t_K(b_ЗСcек)=0,25 сек [203] и d_K(b_ЗС)=5,5×10^{-4 см [}233], длина капилляра l_K(b_ЗС)=220 мкм. С учетом ξ_K(b_ЗС)=1,15×10^-2 Пз получим давление на капилляре DP_K(b_ЗС)=17,4 мм рт. ст. Величина =17,4 мм рт. ст. удовлетворяет следующему условию: при максимальной гипертензии (b_max=2) эта величина не должна превышать величину 35 мм рт. ст., т. к. выше этой величины начинается отек тканей [25, с. 1381]. Очевидно, что величина 17,4 мм рт. ст. является оптимальным значением, разделяющим «противоположности» в диапазоне возможных величин DP_K(b_ЗС). Скорость движения эритроцитов, равная 880 мкм с^-1, не превышает предельную скорость в капиллярах в покое, равную 1000 мкм с^-1 [84]. Необходимо заметить, что возможны колебания скорости эритроцитов в одном и том же капилляре, связанные с нерегулярным перемещением лейкоцитов. Однако установлено [66, т. 3, с. 180], что средняя скорость эритроцитов в течение 15 сек в смещенные интервалы времени практически одинакова. Следовательно, общее количество кислорода, отдаваемое эритроцитами за одинаковые интервалы времени приблизительно постоянно.

Рассмотрим энергетические соотношения в золотом режиме гипертензии. Механическая мощность W_М_K(b_ЗС), расходуемая в ветви (капилляре),

W_М_K(b_ЗС) = = 0,5k_L(b_ЗС)k_x(b_ЗС)W_М_C(b_ЗС), (4.1)

где W_М_C(b_ЗС), W_М_K(b_ЗС) – механическая мощность, расходуемая в стволе и капилляре, k_L(b_ЗС)=l_K(b_ЗС)/l_C(b_ЗС)>>1, k_x(b_ЗС)=x_K(b_ЗС)/x_C(b_ЗС)<1 – соответственно «нестандартные» коэффициенты перехода от ствола к капилляру по длине и вязкости крови. При известных значениях b_k(b_ЗС) = 19300эрг, x_C(b_ЗС)=1,25×10^-2 Пз, x_K(b_ЗС)=1,15×10^-2 Пз, l_C(b_ЗС)= 41,4 мкм и l_K(b_ЗС) = 220 мкм величина k_L(b_ЗС)=5,3 и k_x(b_ЗС)=0,94.

Химическая мощность, расходуемая в капилляре,

W_XK(b_ЗС) = (p/4)b_K(b_ЗС)d_K(b_ЗС)²l_K(b_ЗС). (4.2)

Можно показать, что

W_MK(b_ЗС) = 0,5k_L(b_ЗС)k_x(b_ЗС)W_M_С(b_ЗС) » 2,5W_MC(b_ЗС), (4.3)

W_XK(b_ЗС) = 0,5k_L(b_ЗС)k_x(b_ЗС)W_X_С(b_ЗС) » 2,5W_X_С(b_ЗС), (4.4)

где W_MC(b_ЗС), W_X_С(b_ЗС) – соответственно механическая и химическая мощность, расходуемая в стволе в золотом режиме гипертензии.

Из сравнения (4.3) и (4.4) очевидна полная аналогия относительных изменений механической и химической мощностей в капиллярах. Расход суммарной мощности в 2 ветвях (капиллярах) W_1,2(b_ЗС) по отношению к стволу возрастает приблизительно в 5 раз:

SW_кап1,2(b_ЗС) » 5W_С(b_ЗС).

Нами уже было показано, что любой обменный сосуд за единицу времени отдает такое же количество кислорода, что и капилляр такой же длины (см. раздел 3.6). Отдельный капилляр по длине в 5 раз превосходит прекапиллярную артериолу. Следовательно, за единицу времени ветви тройника в сумме отдают кислорода в 10 раз больше, чем ствол (артериола), а потребляемая ими энергия за это время возрастает только в 5 раз. Очевиден выигрыш: «выгоднее» отдавать основной объем кислорода из тех сосудов, где «цена» его минимальна!

Определим доли механической и химической энергии в суммарном расходе энергии в капилляре. В золотом режиме с учетом представленных выше величин q_K(b_ЗС), d_K(b_ЗС), l_K(b_ЗС) и ξ_K(b_ЗС) механическая мощность W_М_K(b_ЗС) = 4,3×10^-5×г×см²×с^-5. Соответственно, с учетом известных величин b_K(b_ЗС), d_K(b_ЗС) и l_K(b_ЗС) химическая мощность W_Х_K(b_ЗС)=8,56×10^{-5 г}×см²×с^-5. Таким образом, в капиллярах, как и в других сосудах, соотношение механической и химической мощностей

γ_K(b_ЗС) = W_М_K(b_ЗС)/W_ХК(b_ЗС) = 0,5.

Общая потребляемая мощность в отдельном капилляре W_K(b_ЗС)=12,86×10⁵ г×см²×с^-5. Следует отметить особенность затрат энергии в капилляре: отношения W_М_K(b_ЗС)/W_K(b_ЗС)=0,334 и W_XK(b_ЗС)/W_K(b_ЗС)=0,666 аналогичны отношению чисел Фибоначчи 1:2. Величина g(b_ЗС) =0,5 аналогична для каждого транспортного и обменного сосуда, в том числе и для капилляров. Она характеризует фибоначчиеву гармонию механической и химической «противоположностей». Очевидна максимальная эффективность этого соотношения для сердечных систем доставки и отдачи кислорода.

4.2.2. Артериолярно-капилярные тройники в режимах гипертензии

В режимах гипертензии коронарный кровоток и количество открытых капилляров возрастают. Экспериментально установлено, что при увеличении активности сердца концентрация воды в сердечной ткани [297], температура крови и тканей [64], размеры и внутренняя конфигурация капилляров [336] остаются без изменений. Тем самым обеспечивается постоянство среды, окружающей капилляры, и постоянство размеров последних независимо от уровня гипертензии.

При гипертензии размеры капилляров и вязкость крови не изменяются:

d_K(b) = d_K(b_ЗС), (4.5),

l_K(b) = l_K(b_ЗС), (4.6)

x_K(b) = x_K(b_ЗС), (4.7)

где d_K(b_ЗС), d_K(b), l_K(b_ЗС), l_K(b), x_K(b_ЗС), x_K(b) – соответственно диаметр, длина и вязкость крови в капилляре в золотом и других режимах гипертензии.

Исходя из (4.5)–(4.7),

V_K(b) = V_K(b_ЗС), (4.8)

G_K(b) = G_K(b_ЗС), (4.9)

где V_K(b_ЗС), V_K(b), G_K(b_ЗС), G_K(b) – соответственно объем и проводимость капилляра в золотом и других режимах гипертензии.

Известно [248], что существует линейная связь между относительными изменениями давления в крупных артериях и микрососудах различных органов и тканей млекопитающих. Следовательно, при увеличении среднего давления в аорте в b раз давление на капилляре

DP_K(b) = bDP_K(b_ЗС). (4.10),

Соответственно, исходя из (4.8)–(4.10),

q_K(b) = bq_K(b_ЗС), (4.11),

t_K(b) = t_K(b_ЗС)/b, (4.12),

где q_K(b), t_K(b) –кровоток и время пребывания эрироцитов в капилляре в режимах гипертензии.

В условиях гипертензии механическая мощность в капилляре:

W_MK(b) = = b²W_MK(b_ЗС). (4.13)

Величина

b_K(b) = b²b_K(b_ЗС),

следовательно, химическая мощность

W_XK(b) = b²W_XK(b_ЗС). (4.14)

Исходя из (4.4), (4.13) и (4.14) очевидно, что

g_K(b) = W_MK(b)/W_XK(b) = W_MK(b_ЗС)/W_XK(b_ЗС) = 0,5. (4.15)

Этот закон имеет универсальный характер и отражает оптимальную «энергетическую» гармонию «противоположностей» в капилляре. Можно сказать, что это отношение является инвариантом энергооптимальной гармонии «противоположностей» для всех сердечных артерий и капилляров покое и при любой гипертензии.

Вследствие недостаточного обеспечения кислородом клеток на более высоком уровне гипертензии происходит включение дополнительного числа капилляров. Перед началом ветвящегося капилляра расположены отдельные мышечные клетки, называемые прекапиллярными сфинктерами. Эти мышечные структуры обеспечивают подключение дополнительного количества капилляров. Механизм подключения дополнительных капилляров рассматривался нами в разделе 3.7. На капиллярном участке происходит увеличение общего количества открытых капилляров в b раз, что обеспечивает возрастание общего кровотока в b² раз. Тем самым подтверждается «сохранение» закона (3.25) и на капиллярном участке.

Вследствие этого на капиллярном участке, также как и на докапиллярном, суммарный расход механической и химической энергии за единицу времени SW_кап1,2(b) возрастает в b³ раз,

SW_кап1,2(b) = b³SW_кап1,2(b_ЗС).

С учетом того, что размеры и вязкость крови в артериоле и капиллярах при гипертензии не меняются, а k_L(b) = k_L(b_ЗС) и k_x(b_ЗС)= k_x(b), то очевидно, что

SW_кап1,2(b) » 5b³W_С(b_ЗС) (4.16)

В итоге можно сказать, что артериолярно-капиллярным тройникам присущи те же соотношения гармонии, что и другим тройникам докапиллярного русла:

W_M_кап(b)/W_X_кап(b) = W_M_С(b)/W_X_С(b)= 0,5. (4.17)

[k(b)H₁(b)]^3/2 + [k(b)H₂(b)]^3/2 = 1, (4.18)

где W_M_кап(b), W_X_кап(b) – общая механическая и химическая энергия, расходуемая в капиллярах за единицу времени, k(b), H₁(b), H₂(b) – коэффициенты, характеризующие архитектонику артериолярно-капиллярных тройников в режимах гипертензии.

Законами (4.17) - (4.18) представлена энергооптимальная гармония «вхождения» «противоположностей» в «простую» систему (сосуд) и в «сложную» систему (артериолярно-капиллярный тройник).

4.3. Особенности кислородного обеспечения миокарда

Отметим, уже в 60-е годы прошлого столетия стало ясно, что реальная картина распределения величин рО₂ в разных точках тканей между сосудами может быть получена только при расчетах в 3-х координатном пространстве, т.е. в реальном пространстве тканей. Первый решающий шаг в этом направлении сделал Грюневальд [261]. Его модель представляла собой объем ткани в виде прямой призмы, у которой капилляры являются вертикальными ребрами. Призма рассекалась параллельными плоскостями, перпендикулярными к капиллярам. Для расчета рО₂ в модели принимались следующие условия:

1. Распределение кислорода рассматривается в объеме ткани, включенной в ячейку капиллярной сети.

2. Транспорт кислорода из капилляров в ткань осуществляется за счет диффузии по его концентрационному градиенту, который пропорционален градиенту напряжений (скорость диффузии кислорода во всем пространстве считается одинаковой, т. к. физические свойства тканей во всем пространстве между капиллярами принимаются одинаковыми).

3. Зависимость между степенью насыщения крови кислородом и уровнем его напряжения в крови капилляра определяется кривой диссоциации оксигемоглобина.

Распределение рО₂ во всем объеме тканей модели для стационарного случая определяется из уравнения:

DрО₂(х,y,z) = A(x,y,z)/Da,

где рО₂ – напряжение кислорода в ткани; D - коэффициент диффузии кислорода; α - коэффициент растворимости кислорода; A - потребление кислорода единичным объемом ткани за единицу времени; t - время; x, y, z – пространственные координаты; Δ - оператор Лапласа.

Модель Грюневальда позволила провести ряд интересных математических экспериментов и обнаружить важные закономерности [261, 69, 306]. Однако модель Грюневальда имеет существенные недостатки. В этой модели капилляры предстают некими «безликими» трубками без диаметра и длины. Нет ссылок на то, что реально капилляры не являются круговыми цилиндрами; фактически они имеют форму круговых усеченных конусов. Не принимаются во внимание скорость диффузии кислорода из сосуда, а также параметры крови в капилляре (вязкость, форма эритроцитов). Совершенно не принимаются в расчет особенности «капиллярного» участка кривой дезоксигенации гемоглобина. В представленном нами системном исследовании эти «забытые» параметры впервые учитываются. Более того, показана важнейшая роль этих, не учитываемых раньше, параметров в организации оптимального кислородного обеспечения сердечной мышцы.

Отметим, диффузия кислорода происходит в аналогичных условиях, несмотря на разницу его потребления в различных регионах сердца. Эта аналогия обусловлена следующими аспектами:

1. Кровь млекопитающих независимо от массы последних имеет полное насыщение кислородом [214].

2. Коэффициент диффузии кислорода в ткань в основном определяется концентрацией воды в органе [348] и в значительной степени его температурой [44а]. Концентрация воды в сердечной ткани постоянна по всему объему сердца [356], а разница температур для различных слоев сердечной мышцы незначительна и не превышает 0,5^оС [249]. Следовательно, коэффициент диффузии кислорода практически постоянен по всему объему сердца.

3. Коэффициент растворимости кислорода в сердечной ткани в умеренной степени зависит от температуры [261]. Поскольку разница температур во всех регионах сердца незначительна, то коэффициент растворимости кислорода – постоянная величина по всему объему сердца.

4. Величина гематокрита, определенная путем центрифугирования порции крови из микрососудов и капилляров, практически не отличается от гематокрита крови из транспортных и обменных сосудов [281]. Это означает, что гематокрит крови, движущейся через микрососуды и капилляры, постоянен и не зависит от их диаметра.

5. Размеры эритроцитов различных видов млекопитающих практически одинаковы [226].

6. Произведение величины площади поверхности эритроцита на их число в единичном объеме крови млекопитающих – величина постоянная [217].

7. Концентрация гемоглобина в крови различных видов млекопитающих практически одинакова [214].

Перечисленные выше условия сохраняются по всему объему сердца в течение всего кардиоцикла. Также сохраняется во времени и пространстве постоянство других аспектов конструкции капиллярного русла: неизменность размеров микрососудов, их параллельность мышечным волокнам и «смещенное» расположение артериальных и венозных концов соседних капилляров (см. рис. 4.1).

Рис. 4.1. Капиллярно-тканевая призма. а, в – артериальные и венозные концы капилляров; k - сечение, перпендикулярное капиллярам; đ(β_ЗС)- расстояние между капиллярами (ребрами) в золотом режиме гипертензии; l_k – длина капилляра.

Рис. 4.2 Представление сети открытых капилляров миокарда в виде усредненной квадратной решетки в золотом режиме гипертензии. đ(b_ЗС)- расстояние между капиллярами

В то же время абсолютные значения кровотоков и утилизация кислорода одномоментно могут значительно различаться в отдельных регионах сердца (например, в верхушке и основании, эндокарде и эпикарде) [55, 253]. Значительны расхождения по величине этих параметров и в отдельные моменты кардиоцикла. Однако следует отметить, что большему потреблению кислорода в отдельных регионах соответствует и больший кровоток, и большее количество открытых капилляров. Экспериментально установлено, что для сердца распределение величин кровотока [324], потребления кислорода [261], расстояний между открытыми капиллярами [253] и тканевого напряжения кислорода [354] имеет нормальный характер. Величина среднего напряжения кислорода рО₂ во всех регионах сердца одинакова [274, 269]. Следовательно, «качественная» картина распределения крово-кислородных параметров во времени и пространстве всюду совпадает. Учитывая нормальный закон распределения одних параметров и постоянство других, можно получить усредненную капиллярную сеть, равномерно распределенную по миокарду, с одинаковыми условиями движения крови и отдачи кислорода [193]. Отметим, что капилляры параллельны мышечным волокнам; количество тех и других практически совпадает [270, 85]. Наиболее удобной ячейкой для анализа условий доставки кислорода в клетки является объем ткани в форме параллепипеда. Объем сердечной ткани, снабжаемый кислородом из 4 капилляров, имеет форму прямой призмы с капиллярами в качестве вертикальных ребер (см. рис. 4.1). Эти призмы имеют основанием усредненную квадратную решетку, в каждую ячейку которой включено мышечное волокно (см. рис. 4.2). Эта ячейка в дальнейшем будет использована нами для анализа распределения величин рО₂ по объему призмы. Кислородный «комфорт» миокарда в покое и при любом уровне гипертензии должен соответствовать следующим условиям: 1) кислород должен поступать в клетки в количестве, соответствующем уровню потребления кардиомиоцитов (кислородное обеспечение «по количеству»); 2) напряжение кислорода, поступающего в клетки, должно превышать критическую для данного уровня гипертензии величину рО₂, ниже которой начинается гибель клеток (кислородное обеспечение «по качеству»). Оптимальное сопряжение «количества» и «качества» кислорода в капиллярно-тканевых призмах обеспечивают гармонию адекватного кислородного обеспечения сердца в целом.

4.4. Сопряжение конструкции капилляра с кривой дезоксигенации гемоглобина

Отметим особенности дыхательного пигмента крови. Гемоглобин различных видов млекопитающих связывает одинаковое количество кислорода (1 г Hb c 1,34 см³ О₂) [88]. Установлена также одинаковая концентрация гемоглобина в крови для различных видов млекопитающих (15 г на 100 мл крови) [214]. Показано [232], что форма кривых оксигенации гемоглобина у всех видов млекопитающих имеет S–образную форму. S-образность кривой имеет важное биологическое значение. Если бы кривые оксигенации имели, например, форму прямоугольной гиперболы, то при переходе к низким значениям рО₂ происходила бы моментальная отдача кислорода в виде «взрыва». Кривые же S-образной формы обеспечивают диссоциацию оксигемоглобина не в форме «взрыва», а в виде постепенной и плавной отдачи кислорода на обменном участке (см. раздел 3.6, табл. 4). На молекулярном уровне S-образность формы означает, что связывание кислорода гемоглобином происходит кооперативно, т.е. присоединение кислорода к одному гему облегчает его присоединение к остальным.

Кривая оксигенации гемоглобина HbO₂=f(рО₂), представленная на рис. 3.8, соответствует естественным параметрам крови: рН 7,40, рСО₂=39,7 мм рт. ст. и t=37^оС [176]. По мере продвижения эритроцита по цепочке обменных микрососудов непрерывно возрастает разность между значениями HbO₂=97% и рО₂=95 мм рт. ст. в аорте и их значениями в обменных микрососудах. На основе кривой HbO₂= f(рО₂) нами была построена разностная кривая DрО₂=f(DHbO₂) (см. рис. 4.3) [192], где DрО₂ = 95-рО₂ и DHbO₂ = 97-HbO₂. Разностной кривой соответствует система координат, в которой HbO₂ и рО₂ «поменялись» местами. При построении этой кривой за начало отсчета нами была принята точка с координатами HbO₂=97% и рО₂=95 мм рт. ст. на кривой HbO₂=f(рО₂). Кривая DрО₂=f(DHbO₂) отображает приращения DрО₂ и DHbO₂ в эритроците по мере прохождения последним цепочки обменных сосудов, включая и капилляр. Разностная кривая удобна для анализа закономерностей «кислородного разряда» эритроцита в капилляре. Произведенный нами анализ показал, что в пределах ΔHbO₂ =5,5-68,6% и ΔpO₂=30-76 мм рт. ст. (рис. 4.3, соответственно точки A, B, C, D) кривая ΔpO₂=f(ΔHbО₂) представляет собою сегмент логарифмической кривой [192]:

ΔpO₂= 42lgΔHbO₂. (4.21)

Всякой разности двух значений ΔHbO₂ на логарифмическом участке кривой соответствует величина разности напряжения кислорода:

dpO₂= ΔрО₂(ΔHbO₂*) - ΔрО₂(ΔHbO₂^) = 42lg(ΔHbO₂*/ΔHbO₂^), (4.22)

где ΔHbO₂*, ΔHbO₂^ - значения ΔHbO₂ на логарифмическом участке разностной кривой в пределах 5,5% £ ΔHbO₂ £ 68,6%.

На кривой диссоциации гемоглобина в ее обычном представлении (см. рис. 3.8) логарифмическому» диапазону ΔpO₂=30-76 мм рт. ст. соответствует интервал рО₂=65-19 мм рт. ст., а ΔHbO₂=5,5-68,6% интервал HbO₂=91,5-28,4%. На артериальном конце капилляра в покое рО₂ =50 мм рт. ст. [37, 38], а на венозном конце - рО₂=20 мм рт. ст. [321]. Таким образом, в золотом режиме гипертензии диапазон рО₂(b_зс)=50-20 мм рт. ст. расположен в пределах «логарифмического» участка кривой диссоциации - 65-19 мм рт. ст. Напряжение кислорода на венозном конце капилляра совпадает с нижней границей логарифмического участка, а рО₂на артериальном конце ниже верхней границы логарифмического участка на 15 мм рт. ст. В условиях гипертензии рост среднего аортального давления в b раз вызывает уменьшение разности концентраций кислорода на участках аорта - артериальный конец капилляра и аорта - венозный конец капилляра в b раз. Эти изменения равнозначны уменьшению артерио-венозной разности насыщения

Рис. 4.3. Разностная кривая дезоксигенации гемоглобина человека [192] Размерность по оси абсцисс ΔHbO₂ -. %, по оси координат ΔpO₂ - мм рт. ст. Интервалы AB и CD соответствуют логарифмическому участку кривой, где ΔpO₂=42lgΔHbO₂. Интервал АВ - ΔHbO₂=5,5-68,6%; интервал CD ΔpO₂-=30-76 мм рт. ст. Кривая соответствует рН 7,40, рСО₂=39,7 мм рт. ст. и температуре t =37^оС.

на капилляре в b раз [192, 193]:

a-vHbO_2K(b) = a-vHbO_2K(b_ЗС)/b, (4.23)

где a-vHbO₂_K(b_ЗС), a-vHbO₂_K(b) - разность концентрации кислорода в крови на артериальном и венозном концах капилляра в золотом и других режимах гипертензии. С учетом (4.21)–(4.23), напряжение кислорода на концах капилляра при гипертензии возрастает на одну и ту же величину dpO₂(b)=42lgb [192, 193]. Следовательно, напряжение кислорода на концах капилляра:

apO₂(b) = 50 + 42lgb, (4.24)

vpO₂(b) = 20 + 42lgb, (4.25)

где apO₂(b), vpO₂(b) - соответственно напряжение кислорода на артериальном и венозном концах капилляра в режимах гипертензии. В (4.24)-(4.25) отражены изменения рО₂ в капилляре в различных режимах гипертензии. Максимальной гипертензии (b=2) соответствует приращение dpO₂=12,6 мм рт. ст.; при этой гипертезии скорость эритроцитов в сердечном капилляре по отношению к золотому режиму возрастает в 2 раза. Интересно отметить, что при двукратном увеличении скорости эритроцитов в капиллярах аналогичное приращение (dpO₂=10 мм рт. ст.) получено в различных точках нейрона мозга на модели Грюневальда [67]. Очевидно, что и при максимальном приращении величина рО₂(b) не выходит за верхний предел логарифмического участка кривой насыщения гемоглобина (65 мм рт. ст.). Следовательно, величины рО₂на концах сердечного капилляра никогда не выходят за пределы логарифмического участка кривой. «Вхождение» в эти пределы обеспечивается изменениями в пределах гемодинамических параметров капилляра. Логарифмичность «капиллярного» участка кривой, как будет показано ниже, имеет большое значение для оптимального распределения величин рО₂ в сердечной ткани. Исходя из (4.24) и (4.25), очевидно, что как в покое, так и при любой гипертензии артерио-венозная разность напряжений на капилляре:

a-vpO_2K(b) = 30 мм рт. ст. (4.26)

Благодаря большой крутизне «капиллярного» участка кривой эта разность минимальна, что обеспечивает наименьший разброс величин рО₂ по объему призмы (см. раздел 4.5). Таким образом, при анализе кривой DрО₂=f(DHbO₂) нами установлена оптимальность «капиллярного» сегмента, на котором минимальному изменению DрО₂ соответствует максимальное изменение DHbO₂. На этом сегменте представлена оптимальная гармония «противоположностей» кислородных параметров по количеству и «качеству».

Необходимо отметить аналогию кислородного обеспечения по «количеству» и «качеству» в обменных артериолах и капиллярах. Каждое поперечное сечение капилляров и обменных микрососудов за единицу времени отдает одинаковое количество кислорода и в условиях покоя, и при гипертензии. Давление, приложенное к отдельным сосудам некоторой генерации обменных микрососудов одинаково, что обусловливает равное время пребывания эритроцитов в каждом из этих сосудов. Скорость отдачи кислорода из всякого поперечного сечения микрососудов постоянна и равна 220% с^-1 (см. раздел 3.6). Наличие этих закономерностей означает, что рО₂ на входе и выходе сосудов данной генерации приблизительно одинаковы. В конечном счете, феномен равенства обеспечивает одинаковую разность рО₂ на входе и выходе всех капилляров. Величины рО₂ на входе и выходе обменных сосудов различны и превышают таковые на капиллярах. Однако установлено [71], что уже на незначительном отдалении от стенки обменных артериол рО₂ в ткани резко снижаются до приблизительно одинаковых величин. В то же время у стенок капилляров имеет место пологое падение рО₂. На расстоянии свыше 10 мкм от стенки величины рО₂ в ткани в обоих вариантах приблизительно одинаковы. Следовательно, «качество» и «количество» кислорода, поступающего в клетки из всех обменных микрососудов и капилляров при заданном уровне гипертензии, практически одинаковы для всех сосудов.

Таким образом, на примере тканевой призмы с ребрами-капиллярами нами проанализированы оба фактора кислородного обеспечения клеток: по «количеству» и «качеству». При увеличении среднего аортального давления в b раз «количество» кислорода обеспечивается за счет увеличения числа открытых микрососудов и капилляров в b раз, «качество» – за счет возрастания в b раз скорости эритроцитов в каждом капилляре [193]. Как следствие этих изменений, общий кровоток в капиллярной сети увеличивается в b² раз.

Отметим, что обменные капилляры связаны между собою поперечными капиллярами; последние выполняют роль своеобразных анастомозов. Эту конструкцию можно рассматривать как своеобразный демпфер между открытыми капиллярами. Наличие этих устройств позволяет сбалансировать перепады в гемодинамике различных зон капиллярного русла. Установлено [84], что и в покое, и в условиях рабочей ишемии суммарная длина поперечных капилляров по отношению к суммарной длине всех постоянна и составляет 10%. Очевидно, что это постоянство не является случайным.

Отдает ли эритроцит на каждой единице длины капилляра одно и то же количество кислорода? Покажем, что такое постоянство существует. Отметим, что капилляр имеет форму усеченного кругового конуса (узкий диаметр на артериальном конце и широкий на венозном). Благодаря такой особенности в соответствии с принципом непрерывности эритроциты движутся в капиллярах с замедлением. Каждый эритроцит при движении отдает кислород с постоянной скоростью; однако время пребывания клетки в единичных сегментах капилляра различно. На узком единичном сегменте капилляра, который он успевает «проскочить» быстрее, эритроцит отдает кислорода меньше, чем на более широком. Однако за одно и то же время общее количество эритроцитов, «проскочивших» через узкий сегмент за единицу времени, больше, чем в широком. Вследствие этих обратных относительных изменений каждый единичный сегмент капилляра за единицу времени отдает приблизительно одинаковое количество кислорода.

Отметим еще одно важное обстоятельство. Очевидно, что в цилиндрическом капилляре эритроцит перемещался бы равномерно. В этом случае величина изменения насыщения гемоглобина на каждом единичном отрезке капилляра

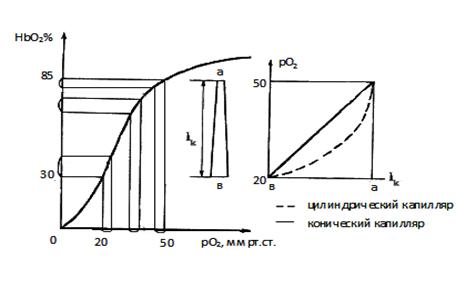
Рис. 4.4. «Распрямление» кривой дезоксигенации гемоглобина HbО₂=f(pO₂) на капилляре [194] .l_k – длина капилляра, а, в артериальный и венозный концы капилляра.

(ΔHbO₂/Δl_к) была бы постоянной. При этом, исходя из формы кривой насыщения, величина ΔpO₂/Δl_к уменьшалась бы на каждой единице длины от артериального конца капилляра к венозному (см. рис. 4.4). Такое изменение ΔpO₂/Δl_к будет происходить при условии: капилляр - круговой цилиндр. Фактически же капилляр является круговым усеченным конусом, поскольку его диаметр на венозном конце больше, чем на артериальном, на 1-2 мкм [362]. Вследствие этого, отдельный эритроцит движется от начала капилляра к концу с возрастающим замедлением, отдавая на каждой единице длины все большее количество кислорода. Отметим, что при этом величина ΔpO₂/Δl_к меняется незначительно (см. рис. 4.4). Таким образом, отношение ΔpO₂/Δl_к остается приблизительно постоянным по всей длине капилляра. Нелинейный «логарифмический» сегмент кривой насыщения как бы «распрямляется» на капилляре. За счет этого феномена обеспечивается приблизительно линейное изменение величины рО₂ по длине капилляров (см. рис. 4.4).

Таким образом, вследствие конусообразной формы капилляров и логарифмичности капиллярного участка кривой насыщения на единице длины капилляра обеспечивается: 1) диффузия одинакового объема кислорода за единицу времени, 2) линейное изменение величины рО₂. Благодаря оптимальному сопряжению «противоположностей» кислородных параметров на каждом единичном сегменте капилляра создаются наиболее благоприятные условия для оптимального кислородного обеспечения призмы по «количеству» и «качеству».

Соотношение между внутренней поверхностью обменного микрососуда S и суммарной поверхностью SS_Э эритроцитов, проходящих мимо внутренней поверхности S, также имеет большое значение в явлениях газообмена. По расчетам, представленным А.Л. Чижевским [208], это соотношение убывает от крупных сосудов к капиллярам. Следует отметить, отношение SS_Э/S капиллярах имеет минимальное значение 1,26 (1,26@). Нами показано (см. раздел 3.4.3), максимальный газообмен происходит в капиллярах, где имеет место наибольшее соотношение поверхности к объему сосуда (S_k/V_K= max). Поэтому несомненно, что в капилляре при отношении SS_Э/S_K=1,26 поверхность сосуда и cуммарная поверхность эритроцитов используются наиболее эффективно. Следует вспомнить, что в капиллярах эритроциты принимают парашютообразную форму [292], при которой эритроциты отдают большее количество кислорода, чем при дискообразной. Следовательно, наибольший уровень газообмена в капиллярах обусловлен не только оптимальным соотношением поверхности сосуда к его объему, но также и оптимальным соотношением поверхности сосуда к общей поверхности эритроцитов. Эти феномены составляет основу наиболее эффективного газообмена между капиллярами и сердечной тканью.

4.5. Распределение рО₂ в капиллярно-тканевыx призмах в режимах гипертензии

Важнейшим фактором оптимизации кислородного обеспечения миокарда по «качеству» является и смещение концов соседних капилляров относительно друг друга. Представим взаимное расположение капилляров в виде прямой призмы, построенной на квадратном основании, с четырьмя перфузируемыми капиллярами в качестве ребер (мышечное волокно проходит внутри призмы) (см. рис. 4.1 и 4.2). Установлено [309], в миокарде кровотоки в соседних капиллярах в преобладающей степени противоположны. Отметим, потребление кислорода сердечной мышцей в течение систолы и диастолы резко различается [294]. Однако существует полная аналогия по «качеству» кислорода между «систолической» и «диастолической» призмами. Это подобие очевидно из следующих экспериментальных данных. В течение кардиоцикла распределение величин рО₂ в крови сердечных капилляров [315], в отдельном кардиомиоците [353] и сердечной ткани [238] неизменно. Отметим, что величина среднего напряжения кислорода рО₂ во всех регионах сердца в течение кардиоцикла одинакова [264, 269]. Отметим также, скорость отдачи кислорода из каждого сечения капилляров, открытых в тот или иной момент сердечного цикла, одинакова. Неизменность «качества» О₂ в различных регионах в любую фазу кардиоцикла возможна только при одном условии. Этот феномен может иметь место, если существует равенство:

V_D(b_ЗС)/V_S(b_ЗС) = B_S(b_ЗС)/B_D(b_ЗС),

где V_S(b_ЗС), V_D(b_ЗС) – объем систолической и диастолической призм, В_S(b_ЗС), В_D(b_ЗС) – средняя скорость потребления кислорода единичным объемом «систолической» и «диастолической» призм за единицу времени в золотом режиме гипертензии. Поскольку призмы имеют квадратное основание и одинаковую высоту, то отношение расстояний между соседними капиллярами в «диастолической» и «систолической» призмах обратно пропорционально отношению скоростей потребления кислорода за систолу и диастолу:

đ_D(b_ЗС)/đ_S(b_ЗС) = , (4.27)

где đ_S(b_ЗС), đ_D(b_ЗС) – «систолическое» и «диастолическое» расстояния между капиллярами в золотом режиме гипертензии. В покое объем потребляемого кислорода миокардом за систолу составляет 91% и 9% в течение диастолы [294], а длительность диастолы превышает интервал систолы в 1,62 раз. Из этих данных следует, что «диастолическая» призма за единицу времени потребляет кислорода в 16,35 раз меньше, чем систолическая. Соответственно, по нашим расчетам отношение В_S(b_ЗС)/В_D(b_ЗС)=16,5, а đ_D(b_ЗС)/đ_S(b_ЗС)=4,07. При этих значениях обеспечивается одинаковое «качество» О₂ в систолической и объемных призмах в любой момент кардиоцикла. Очевидно, что произведение объема систолической призмы на скорость потребления кислорода единичным объемом призмы равно аналогичному «диастолическому» произведению. Это произведение является своего рода инвариантом кислородного обеспечения в любой момент сердечного цикла. Этот инвариант является гарантом того, что по всему объему сердечной мышцы во всякий момент кардиоцикла обеспечивается адекватное кислородное обеспечение по «количеству» и «качеству».

Как было показано нами в разделе 4.4, конусообразность формы капилляра и логарифмичность «капиллярного» участка кривой насыщения обеспечивают одинаковое количество и «качество» потребляемого кислорода по всей длине открытого капилляра. Добавим к этому, совокупность призм построена на квадратной решетке (см. рис. 4.2). С учетом этих факторов рассмотрим, какое значение имеет смещение концов капилляров. Пространственное расположение капилляров имеет следующие особенности: 1) артериальные и венозные концы соседних сосудов (ребер призмы) последовательно смещены на полдлины вверх (или вниз) [337], 2) кровотоки в противоположных капиллярах имеют обратные направления [261]. Как мы уже показали выше, за счет замедления движения эритроцита по капилляру распределение рО₂ по длине капилляра имеет приблизительно линейный характер (см. рис. 4.4). За счет этого феномена обеспечивается линейное распределение рО₂ по длине каждого из 4 капилляров. При переходе от одного сечения призмы к другому приращения величины рО₂ в парах противоположных по диагонали сосудов одинаковы, но противоположны по знаку. Вследствие этого создается приблизительно равное распределение рО₂ во всех сечениях систолических и диастолических призм. Потребление кислорода в течение систолы во всех сечениях «систолических» призм и в течение диастолы в «диастолических» одинаково. Таким образом, гармония «смещенного» сопряжения капилляров, каждый из которых занимает в призме оптимальное положение, обеспечивает одинаковое «качество» кислорода по всей высоте призмы (см. рис. 4.5, А). При любом другом взаимном смещении капилляров была бы нарушена аналогия оптимального распределения рО₂ во всех сечениях призм.

4.5. Распределение рО₂ в капиллярно-тканевыx призмах в режимах гипертензии

Рассмотрим распределение рО₂ в капиллярно-тканевых призмах в золотом и других режимах гипертензии. В заданном режиме гипертензии потребление кислорода единичным объемом мыщцы в каждый момент кардиоцикла увеличивается в b раз. Соответственно, плотность капилляров, открытых в систолу и диастолу, также возрастает b раз, что соответствует сокращению расстояния между сосудами в раз и, соответственно, уменьшению объема призм в b раз. При заданном уровне гипертензии b систолическая призма А превращается в систолическую призму Б (см. рис. 4.5). Очевидно, что потребление кислорода «гипертензивной» призмой Б равно потреблению исходной призмы А; это равенство сохраняется при всех уровнях гипертензии. Исходя из (4.27), та же аналогия имеет место и для всех диастолических призм.

Рис. 4.5. Капиллярно-тканевая призма. А – в золотом, Б – в режиме гипертензии; l_K(β_ЗС), l_K((β) - длина капилляра в золотом и других режимах гипертензии, l_K((β)=l_K(β_ЗС); đ(β_ЗС), đ(β) - расстояние между капиллярами в золотом и других режимах гипертензии; đ(β)=đ(β_ЗС)/Öb.

Рис. 4.6. Пространственное расположение цепочек параллельных капилляров.

а, в – артериальный и венозный концы капилляров. Заштрихованные плоскости – поперечные сечения капиллярно-тканевой призмы.

требление кислорода систолическими и диастолической призмами за единицу времени при любой гипертензии всегда одинаково и равно общей исходной величине в золотом режиме. Таким образом, сердечная мышца в любой момент времени при любой гипертензии состоит из «призм», каждая из которых за единицу времени потребляет одинаковое количество кислорода. Покажем особенности аналогии распределения рО₂ по длине мышечного волокна в золотом режиме гипертензии. На протяжении отдельного мышечного волокна существует последовательность капиллярно-тканевых призм (см. рис. 4.6). Выберем в качестве исходного сечение одной из призм на уровне, соответствующем артериальному и венозному концам двух противоположных капилляров. При смещении от этого сечения на полдлины капилляра вниз распределение рО₂ в данном сечении «поворачивается» на 90° относительно продольной оси волокна. При последующих смещениях вниз на полдлины капилляра исходное распределение «поворачивается» соответственно на 180^о и 270^о. При смещении вниз на 2 длины капилляра распределение рО₂ совпадает с исходным. При последующем смещении через каждые 2l_K цикл винтового «поворота» повторяется. Очевидно, что и при смещениях на углы в пределах 0^o<y<90^o, 90^o<y<180^o, 180^o<y<270^o, 270^o<y<360^o распределение рО₂ от исходного отличается незначительно. Таким образом, распределение рО₂ в поперечных сечениях мышечного волокна происходит в соответствии с винтовой симметрией. Такое пространственное сопряжение капилляров обеспечивает одинаковые условия для «качественного» кислородного обеспечения кардиомиоцитов по всей длине мышечного волокна. Благодаря этому обстоятельству в золотом режиме гипертензии ни один из кардиомиоцитов, составляющих мышечное волокно, не находится в менее благоприятных «кислородных» условиях, чем остальные. Гармония «противоположностей» в распределении концов капилляров по длине мышечного волокна создает условия

оптимального распределения величин рО₂ по всей длине мышечного волокна. В конечном счете, форма капилляров, параллельность и винтовая симметрия их пространственного расположения по отношению к мышечным волокнам обеспечивают оптимальное сопряжение (гармонию) «качественного» и количественного обеспечения кислородом любого участка мышечного волокна и сердечной мышцы в целом.

Рассмотрим аналогию распределения рО₂ в условиях гипертензии. Выберем для сравнения некоторые k-сечения призмы А (покой) и призмы Б (гипертензия), равноудаленные от основания (см. рис. 4.1 и 4.5). Распределение плотности рО₂ в k-сечении призмы А соответствует некоторой кривой I (см. рис. 4.7). В капиллярах призмы Б k-сечении напряжение кислорода при гипертензии b возрастает на величину dpO₂=42lgb. Поскольку потребление кислорода в обоих k-сечениях одинаково, то кривая распределения рО₂ в k-сечении призмы Б смещается вправо на величину dpO₂ (см. рис. 4.7, кривая II). Очевидно, что аналогичное смещение распределения рО₂ происходит и в других сечениях призмы Б. С физиологической точки зрения сдвиг кривых распределения в сторону больших значений имеет важное значение. Установлено [289], что при снижении в кардиомиоцитах средней величины рО₂ ниже 3,4-3,6 мм рт. ст. начинается фибрилляция сердца, свидетельствующая о кислородной недостаточности. Параллельный сдвиг вправо позволяет вывести клетки из летальной зоны (при росте гипертензии эта зона расширяется в сторону более высоких рО₂).

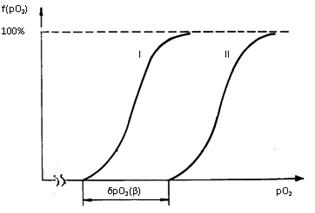
Рис. 4.7. Плотность распределения величин рО₂ в k–сечении капиллярно-тканевой призмы [193]. По оси абсцисс – рО₂ (условные единицы); по оси ординат – долевое распределение рО₂ в k-сечении призмы (в %). I – распределение рО₂ в золотом, II – распределение рО₂ в некотором режиме гипертензии; δpO₂(β)=42lgβ – приращение рО₂ на концах капилляра в режиме гипертензии.

Поскольку при гипертензии b в каждом сечении призм и капилляров приращения dpO₂(b) одинаковы, то постоянна и разность напряжений кислорода между кровью и тканью. Как следствие, постоянна и скорость отдачи кислорода движущимся эритроцитом [291]. Эта скорость неизменна по всей длине открытого сердечного капилляра в любой момент кардиоцикла в покое и при любой гипертензии. Она имеет, как было показано в 3 главе (см. раздел 3.6), для любого поперечного сечения каждого капилляра максимально возможное значение:

U(b) = 220%/c.

Эта величина является кислородным инвариантом всего капиллярного русла сердца. Механизм «винта» обеспечивает в каждом сечении мышечного волокна одинаковое «количество» и «качество» кислорода, адекватное заданному уровню гипертензии.

Подытожим. На примере тканевой призмы с ребрами-капиллярами нами проанализированы оба аспекта кислородного обеспечения клеток - по «количеству» и «качеству». Первый параметр в условиях гипертензии обеспечивается увеличением плотности капиллярной сети в b раз, второй - возрастанием линейной скорости эритроцитов в капиллярах также в b раз. Оба параметра связаны с увеличением среднего аортального давления в b раз. Можно сказать, Природа из диапазона возможных величин плотности капилляров, их взаимного расположения и возможных скоростей эритроцитов в капиллярах «выбрала» «рабочие» величины, оптимальные для каждого уровня гипертензии. Рабочие значения этих параметров разделяют диапазон допустимых значений на «противоположности». При всяком уровне гипертензии существует оптимальная гармония «противоположностей» для каждого из этих параметров. Это сопряжение позволяет обеспечить энергооптимальное снабжение кислородом любого региона сердечной мышцы как в покое, так и при всяком уровне гипертензии.

Следует отметить инварианты, присущие капиллярно-тканевым призмам в течение всего сердечного цикла в золотом и любом другом уровне гипертензии:

1. постоянство скорости отдачи кислорода из каждого открытого капилляра;

2. постоянство разности рО₂ на артериальном и венозном концах капилляров;

3. постоянство «винтового» распределения рО₂ вдоль мышечного волокна;

4. постоянство потребления кислорода объемами систолических и диастолических призм за единицу времени.

Выше нами были рассмотрены полностью «капиллярные» призмы (все ребра - капилляры). Рассмотрим призму, у которой артериола - одно из ребер. В сущности, как поставщики кислорода обменные артериолы почти ничем не отличаются от капилляров. Отметим ряд факторов архитектоники и гемодинамики, аналогичных для артериол и капилляров. Как мы уже отмечали раньше, стенки мельчайших артериол имеют строение, весьма сходное со строением капилляров: эпителий, тончайшая базальная мембрана и сравнительно редкие и очень тонкие пучки гладких мышц. Все эти образования имеют такой же коэффициент диффузии для О₂ и СО₂, как и окружающие ткани [66, т. 3, с. 182]. Обменные артериолы, также как и капилляры, параллельны мышечному волокну, которое они обеспечивают кислородом [270, 55]. Показано также [46], что при естественном отношении S/V энергия деформации мембраны эритроцитов минимальна. Вследствие этого свойства изменение формы эритроцитов в микрососудах происходит с минимумом потерь энергии. Эритроциты при перемещении в артериолах с диаметром менее 40 мкм так же, как и в капиллярах, принимают парашютообразную форму [326], которая обеспечивает оптимальные условия для отдачи кислорода [292]. В артериолах, как и в капиллярах, отношение средних скоростей движения эритроцитов и плазмы приблизительно равно 1,6, т. е. золотому числу [230, 282]. Как нами показано выше, каждое сечение артериол, независимо от их диаметра, отдает за единицу времени то же количество кислорода, что и сечение капилляра. Обьем отданного кислорода той или иной артериолой за единицу времени зависит лишь от ее длины, но не от диаметра. С «кислородной» точки зрения артериола фактически тот же капилляр. Таким образом, «включение» артериол в призму вместо капилляров ничего не меняет за исключением одного обстоятельства – величины рО₂ на концах артериол значительно больше, чем на концах капилляров. Однако в тканях и это различие нивелируется по мере удаления от стенки сосудов. Показано [247], что чем больше диаметр артериол, тем менее они проницаемы для кислорода, тем больше падение рО₂ на стенке. У капилляров при небольшом удалении от стенки сосуда снижение тканевого рО₂ по отношению к крови незначительно. В то же время при таком же удалении от стенки артериол величина рО₂ резко снижается, почти достигая «капиллярных» значений [71]. При дальнейшем удалении от стенки снижение рО₂ происходит по аналогии с капиллярами. Следовательно, «вставка» артериолы вместо капилляра в плане адекватного обеспечения кислородом по «качеству» и «количеству» тканей практически ничего не меняет – распределение рО₂ в любом сечении призм во всех режимах гипертензии сохраняется таким же, что и при «капиллярном» варианте. Однако между артериолами и капиллярами есть существенное различие. Разница состоит в «цене» потребляемого из них кислорода: энергетическая «стоимость» единичного объема кислорода, потребляемого из артериол, выше, чем в капиллярах.

Заключение. Гармония оптимального сопряжения «противоположностей» архитектонических, гемодинамических и кислородных параметров в системе «Капиллярно-тканевая призма» обеспечивает оптимальное кислородное обеспечение последней по «количеству» и «качеству» с минимальными затратами энергии, крови и сосудистого материала во всех режимах гипертензии.

4.7. «Цена» потребляемого кислорода в режимах гипертензии

Произведем расчет «цены» транспорта единичного объема кислорода через капиллярный участок в режимах гипертензии.

Сопротивление обменного участка при гипертензии изменяется путем введения в функциональное состояние части резервных артериол и прекапиллярных сфинктеров, составляющих предпоследнюю генерацию артериол, предшествующую капиллярам. Работа сфинктера колеблется между открытым и полностью закрытым состояниями [268]. В начале гипертензии в кардиомиоцитах возникает недостаток кислорода, клеточное рО₂ падает, что вызывает увеличение концентрации веществ Рi и 5¢АМФ с последующим расслаблением мышцы прекапиллярных сфинктеров и раскрытием капилляров. Каждый резервный капилляр раскрывается в ответ на «свою» величину гипертензии. Очевидно, для того, чтобы сохранялся закон (3.24), при каждом возрастании давления в аорте в b раз происходит увеличение общего количества открытых капилляров также в b раз за счет подключения новых капилляров. При этом общий кровоток через капиллярный участок увеличивается в b² раз, поскольку давление на каждом открытом капилляре возрастает в b раз.

Легко показать, что расход мощностей на капиллярном участке за сердечный цикл в режиме гипертензии:

W_K(b) = b³W_K(b_ЗС),

где W_K(b_ЗС), W_K(b) – общая мощность в капиллярном русле в золотом и других режимах гипертензии.

Общий расход мощности в капиллярном русле при гипертензии увеличивается в b³ раз, а средняя за сердечный цикл скорость потребления кислорода сердечной мышцей возрастает в b² раз [193]. Очевидно, что с ростом гипертензии «цена» единичного объема кислорода, отдаваемого из капилляров за единицу времени, также как и у обменных сосудов, возрастает в b раз:

ζ_K(b) = bζ_K(b_ЗС), (4.35)

где ζ_K(b_ЗС), ζ_K(b) – энергетическая «цена» единичного объема кислорода, потребляемого из капиллярного русла за единицу времени в золотом и других режимах гипертензии.

На капиллярном участке Природа создала оптимальное сопряжение минимального расхода энергии на транспорт кислорода с наиболее эффективным потреблением последнего. Отметим, для каждого транспортного и кислородного параметра найдена оптимальная гармония «противоположностей». Очевидно, что самый «дешевый» кислород в капиллярах имеет место в золотом режиме гипертензии (b=b_ЗС=1), а наибольшая «цена» потребляемого кислорода соответствует режиму максимальной гипертензии (b=2). Для всех генераций обменных артериол также имеют место выражения, аналогичные (4.35). Различие заключается в том, что чем дальше расположены артериолы от капилляров, тем выше «цена» потребляемого из них кислорода. На капиллярном участке в сердечную мышцу поступает свыше 85% от всего кислорода, потребляемого миокардом. Следовательно, основная часть кислорода поступает в ткани при наименьших затратах энергии. Добавим к этому, наиболее выгодный режим гипертензии (покой) составляет наибольшую часть протяженности жизни животных. Таким образом, кислородное обеспечение сердца человека и млекопитающих в течение жизни в основном осуществляется при самой минимальной энергетической «цене»!

4.8. Капиллярно-тканевая система и теплообмен в сердечной мышце

Кроме газообмена гемососудистая система имеет еще одну важнейшую функцию - обеспечение теплообмена между тканями и кровью. Теплообмен между тканями и кровью в основном осуществляется на капиллярном участке кровеносного русла. Отметим, капилляры конструктивно в максимальной степени «приспособлены» для теплообмена. Эффективный обмен обеспечивается, прежде всего, минимальной толщиной стенки этих сосудов. Кроме того, капилляр имеет максимальное по сравнению с другими микрососудами отношение площади обменной поверхности к объему. Различная плотность капиллярной сети в различных регионах миокарда позволяет создать в последних адекватные условия для отвода избыточного тепла, производимого в кардиомиоцитах. «Подбор» минимально возможного диаметра капилляров и микрососудов и их параллельное размещение по отношению к мышечным волокнам позволяет наиболее эффективно удалять избыточное тепло из клеток, чтобы предотвратить их «перегрев». Плотность капиллярной сети такова, что по всему объему миокарда в каждой клетке соблюдается оптимальное соотношение между количеством производимого и удаляемого тепла в узком физиологическом диапазоне температур.

Рассмотрим производство тепла в кардиомиоцитах. Известно [199], что энергия, производимая в клетке при расщеплении молекул гексозы, распределяется в клетке в следующем долевом соотношении «противоположностей»: химически связанная в АТФ – 38,3% и рассеянная в виде тепла - 61,7%. Такое распределение соответствует золотой гармонии «противоположностей» - тепловой и связанной форм энергии. Именно при таком соотношении «противоположностей» в клетках поддерживается «золотая» температура 38^оС, которая разделяет температурный диапазон воды по пропорции золотого сечения. «Выбор» в клетках температуры, близкой или равной 38^оС, отнюдь не является «случайностью», поскольку эта температура воды обеспечивает в клетках наиболее энергетически экономное и быстрое течение процессов жизнедеятельности.

Установлено [245], что между утилизацией кислорода и выделением тепла в сердечной мышце существует прямая линейная зависимость. При увеличении давления в аорте в b раз в той же степени возрастает потребление кислорода, образование АТФ и производство тепла в сердечных клетках. Одновременно в b раз возрастает плотность капиллярной сети и обменных микрососудов; при этом общая обменная поверхность и объем сосудов увеличивается в той же мере. Количество единичных объемов крови, проходящих через капиллярное и микрососудистое русло за единицу времени при гипертензии, также возрастает в b раз [203]. Вследствие этого устраняется перегрев крови в капиллярах и клетках, что имеет большое значение для оптимального протекания биопроцессов в последних. Увеличение плотности открытых капилляров при гипертензии позволяет поддерживать температуру сердечной ткани и крови приблизительно на одном и том же уровне, что чрезвычайно важно, поскольку температура внутренних тканей и органов млекопитающих колеблется в узкой биокинетической зоне 37-38,5^оС [64]. Постоянство температуры крови и кардиомиоцитов является одним из важнейших условий оптимального функционирования гемокапиллярно-тканевой системы сердца. Отметим при этом, величина 38^оС разделяет температурный диапазон жидкой фазы воды в соответствии с золотой пропорцией «противоположностей».

Тепло, как и кислород, имеет два аспекта: «количество» и «качество». Под «количеством» следует понимать тепло, производимое за единицу времени, температура же производимого тепла является «знаком» его «качества». Чрезвычайно важно отметить, что тепло отнюдь не «бесполезно» рассеивается в крови и кардиомиоцитах. За счет этого тепла поддерживается оптимальная температура около 38^оС, при которой биологические процессы в клетках и крови протекают с максимальной скоростью. Таким образом, можно сказать, что в капиллярно-тканевых призмах сердца существует гармония (оптимальное сопряжение) между «противоположностями» конструктивных, гемодинамических, кислородных и температурных параметров.

4.9. Источники экономии энергии и сосудистого материала в гемокапиллярной системе сердца

Вначале рассмотрим оптимальность сопряжения гемодинамических и кислородных параметров в системе «Капилляр c движущейся кровью».

Прежде всего, отметим энергетический аспект, связанный с минимальной величиной суммарного расхода механической и химической энергии в каждом капилляре. Добавим к этому, что все конструктивные, гемодинамические и кислородные параметры, так или иначе, обусловливающие оптимальность «противоположных» затрат энергии, имеют оптимальные значения. Начнем с того, что величина d_k=5,5 мкм [231] соответствует минимально возможной величине вязкости крови; при дальнейшем сужении сосудов вязкость крови резко возрастает [240]. К этому следует добавить, что при минимально возможном диаметре капилляра имеет место максимальное отношение поверхности к объему (S/V=max), что обеспечивает максимальный уровень обмена между кровью и кардиомиоцитами. Эритроциты при перемещении в капиллярах принимают парашютообразную форму [326], которая обеспечивает наиболее благоприятные условия для отдачи кислорода [292]. Эритроциты в капиллярах отдают кислород с максимальной скоростью 220% с^-1. Время пребывания эритроцитов в капилляре t_K(b_ЗС)=0,25 сек соответствует их «кислородному разряду» на наиболее крутом участке кривой насыщения гемоглобина. С учетом энергооптимальной величины b_K(b_ЗС)=19300 эрг см^-3 с^-1 [295] и оптимальных величин d_K(b_ЗС)=5,5 мкм, t_K(b_ЗС)=0,25 сек оптимальная длина капилляра l_K(b_ЗС)=220 мкм.

Отметим, что при этих величинах линейная скорость эритроцитов в капилляре составляет 880 мкм с^-1, что соответствует экспериментальным данным [208, 111]. Вокруг эритроцита образуется высокочастотное электрическое поле, которое создает между поверхностью эритроцита и стенкой капилляра эффект скольжения и препятствует прилипанию. Время пребывания эритроцитов в капилляре зависит не только от длины капилляра, но также и от величины приложенного давления ΔP_K(b_ЗС). Давление на артериальном конце капилляра даже при максимальной гипертензии (b=2) не должно превосходить величину 35 мм рт. ст., выше которой начинается отек тканей. С учетом максимальной гипертензии давление на артериальном конце капилляра в золотом режиме не должно превышать 17,5 мм рт. ст. В соответствии с оптимальными величинами d_K(b_ЗС)=5,5 мкм, l_K(b_ЗС)=220 мкм, t_K(b_ЗС) =0,25 с и ξ_K(b_ЗС) =1,15×10^-2Пз величина P_K(b_ЗС)=17,4 мм рт. ст. Эта величина близка к значениям, представленным А.Л. Чижевским [208] и не превышает 1/6 систолического давления в аорте [206]. Таким образом, очевидна оптимальность «вхождения» множества оптимальных «противоположностей» архитектонических и гемодинамических параметров в систему «Капилляр с движущейся кровью». В каждом случае «рабочая» величина параметра делит диапазон возможных значений на «противоположности» оптимальным образом. Мы имели возможность убедиться, что гармония «противоположностей» обусловливает оптимальное вхождение конструкционных и гемодинамических параметров в систему «Капилляр с движущейся кровью».

Рассмотрим сопряжение оптимальных значений гемодинамических параметров с оптимальными величинами кислородных параметров в отдельном капилляре. Время пребывания эритроцита в капилляре t_K(b_ЗС)=0,25 cек сопряжено с пределами наиболее выгодного, «крутого» участка кривой насыщения гемоглобина. Эритроцит, «разряжаясь» за время движения по капилляру, полностью «вписывается» в логарифмический сегмент кривой ΔHbO₂_K(b_ЗС) = 85 - 55%. На этом сегменте диффузия кислорода соответствует минимальной разности ΔрО₂ на концах капилляра, что обеспечивает наименьший разброс величин рО₂ по объему сердечной призмы. При вхождении в капилляр эритроцит принимает парашютообразную форму [326]. При парашютообразной форме эритроцит отдает кислород со значительно большей скоростью (~в 2 раза), чем при цилиндрической [292]. Таким образом, при максимальной величине диффузии кислорода 220% сек^-1 [301, 211] «парашюты» в капиллярах отдают необходимое количество кислорода за более короткое время. Этот феномен позволяет получить необходимую разность DpO₂ на капилляре при минимальном приложенном давлении. В разделе 3.6 нами было показано, что транспорт единичного объема кислорода имеет в капиллярах энергетическую «цену», меньшую, чем в любой другой генерации микрососудов. Отдельный капилляр, имея энергооптимальную «гемодинамическую» организацию, одновременно имеет оптимальную «диффузионную» (коническая форма сосуда, парашютообразная форма эритроцитов, максимальная скорость отдачи кислорода). Между диаметром и длиной капилляра, скоростью движения в нем эритроцитов, «способом» отдачи кислорода и временем диффузии в капилляре имеется определенное энергооптимальное «согласование». Можно сделать вывод, что имеет место оптимальное сопряжение между двумя «ипостасями» капилляра: – гемодинамической и диффузионной.

Проанализируем основные источники экономии капилляров.

Важнейшим фактором экономии капилляров является максимальная скорость диффузии кислорода из этих сосудов. При парашютообразной форме в капилляре эритроцит отдает кислород со значительно большей скоростью, чем при цилиндрической. Парашютообразная форма эритроцитов позволяет уменьшить длину обменных микрососудов и капилляров и снизить приложенное к ним давление. Вследствие этого имеет место экономия энергии и сосудистого материала на отдельном капилляре. Кроме того, кислородное обеспечение сердечной ткани при максимальной скорости диффузии позволяет уменьшить количество капилляров, что равносильно снижению плотности капиллярной сети.

Капилляры, как мы уже отмечали выше, являются звеньями диффузионных цепочек. Пространственное расположение этих цепочек представлено в системе «Капиллярно-тканевая призма» (см. рис. 4.6). Эта система является первичной ячейкой системы капиллярно-кислородного обеспечения сердца. Показано [261], что наименьший разброс величин рО₂ в сечениях призмы при прочих равных условиях соответствует смещению концов соседних капилляров (ребер) относительно друг друга на полдлины капилляра. При таком последовательном смещении обеспечивается практически одинаковое распределение величин рО₂ в каждом сечении призмы. При любом другом смещении капилляров аналогичность распределений по длине мышечного волокна нарушается. Как следствие этого, минимальные рО₂ в некоторых сечениях призмы имели бы меньшую величину, чем в оптимальном варианте. Для компенсации этого недостатка потребовалась бы увеличение плотности капиллярной сети, чтобы в «слабых» сечениях достигнуть допустимой минимальной величины рО₂. Таким образом, оптимальное взаимное смещение капилляров в капиллярно-тканевой призме также позволяет снизить плотность капиллярной сети. В разделе 4.10 нами будут представлены дополнительные факторы снижения плотности капилляров, связанные со структурой кардиомиоцитов.

Капиллярная сеть является ядром гемососудистой системы любого органа. Естественно, что минимизация плотности капиллярной сети означает дополнительную экономию энергии, крови и сосудистого материала также и в эластических, и мышечных, и обменных генерациях коронарного русла.

Заключение. Система «Капилляр с движущейся кровью» во всех аспектах (гемодинамическом, диффузионном, температурном и пространственном) входит в систему «Капиллярно-тканевая призма» оптимальным образом, обеспечивая при этом минимальную плотность капиллярной сети сердца. Оптимальные «противоположности» всех параметров обусловливают максимально возможную экономию энергии, крови и сосудистого материала.

4.10. Оптимальность сопряжения структуры кардиомиоцитов и капиллярной сети

Во всех сердечных системах, рассмотренных нами раньше, мы неизменно выявляли экономию энергии и строительного материала. В нашу задачу входит показать: жизнедеятельность кардиомиоцитов должна обеспечиваться минимальным количеством клеточных компонентов и минимумом расходуемой энергии. «Присутствие» этих аспектов экономии в деятельности мышечных клеток сердца представлено нами ниже.

Важнейшим фактором экономии энергии и вещества в кардиомиоците является структура актин-миозиновой системы. Саркомер является элементарной сократительной единицей мышечного волокна. Характерной особенностью саркомера является параллельное расположение в нем актиновых и миозиновых нитей (см. рис. 4.9). Строгая параллельность нитей имеет большое значение, поскольку в этом варианте суммарное усилие саркомеров равно максимальной величине. В покое в конце диастолы длина растянутого саркомера составляет 2,2 мкм; именно этой длине соответствует максимальная мощность последующего сокращения [327, 329] при минимуме потребления кислорода на единицу производимой работы [325]. Для создания адекватной силы сокращения использование наиболее сильных саркомеров позволяет мышечной клетке обойтись минимальным их количеством [344]. «Сильные» саркомеры потребляют минимум кислорода; вследствие этого снижается плотность капиллярной сети.

Следует отметить математические особенности конструкции саркомеров. Длины актиновых и миозиновых нитей в саркомере соответственно составляют 1 и 1,5 мкм, т.е. соотносятся как числа Фибоначчи (2:3). Длина саркомеров в конце диастолы составляет 2,2 мкм, в конце систолы – 1,73 мкм [327, 329]. При сокращении длина мышечного элемента уменьшается в 1,272 раз (1,272=). Таким образом, очевидно «участие» золотого числа 1,618 и чисел Фибоначчи в «подборе» конструкции энергооптимального силового элемента.

Вода в клетке при температуре 38^оС имеет квазикристаллическую структуру. При этой температуре теплоемкость воды минимальна и поэтому расход энергии для поддержания этой температуры в клетках минимален [23]. Таким образом, поддержание «золотой» температуры в кардиомиоците обеспечивает дополнительную экономию затрат энергии на поддержание жизнедеятельности клетки.

Рассмотрим оптимизацию сопряжения «качества» и «количества» кислорода с особенностями структурных элементов кардиомиоцитов. Движение молекул кислорода к месту потребления происходит сложным путем - из крови через стенку сосуда и межклеточное пространство в цитозоль и митохондрии клетки. Движение кислорода в кардиомиоците происходит двояко: 1) за счет свободной диффузии и 2) перемещение молекулами миоглобина [91]. Отметим, роль миоглобина в кислородном обеспечении миоцитов очень велика. Именно способность молекул миоглобина выполнять функции связывания и транспорта кислорода позволяет обеспечить бесперебойный поток последнего в систему окислительного фосфорилирования. Миоглобин быстро насыщается кислородом, его оксигенация остается постоянной в течение всего сердечного цикла. За счет оксимиоглобина минимизируется гетерогенность снабжения кислородом из капилляров [256]. Кроме этого, молекулы миоглобина действуют как «ловушки», которые предотвращают перемещение молекул кислорода из того или иного капилляра в сегменты соседних капилляров с более низким рО₂. Установлено [322], что в области ниже 5 мм рт. ст. миоглобин отдает резерв кислорода, который составляет около 40% от всего количества, поступающего в клетку. Таким образом, «противоположности» - доли «миоглобинного» и «диффузионного» кислорода - соотносятся между собою как числа Фибоначчи (2:3).

С химической точки зрения своеобразие жизни заключается не в особенностях состава или реакций, но в упорядоченности структур и реакций, протекающих с минимальными энергетическими затратами. Эйген и Винклер [220, с. 96] пришли к выводу, «в живых организмах скорость химических реакций всегда достигает предельного значения, которое определяется законами физики». Установлено [321], что при рО₂=5,3 мм рт. ст. цитохромоксидаза в митохондриях кардиомиоцита дышит с максимальной скоростью. Величина рО₂ в молекулах миоглобина и на цитохрохсидазе поддерживается в среднем около рО₂=5,3 мм рт. ст. [269]. Добавим к этому, скорость дыхания сердечных митохондрий также максимальна при естественной для внеклеточной среды величине рН 7,40 [234]. Таким образом, максимальная скорость дыхания митохондрий обеспечивается в естественных условиях жизнедеятельности мышечной клетки. Как следствие, кардиомиоцит для адекватного обеспечения своей жизнедеятельности «обходится» минимальным количеством митохондрий.

Необходимо рассмотреть сопряжение дыхательных пигментов крови и кардиомиоцита - гемоглобина и миоглобина. «Капиллярный» участок на кривой HbO₂ = f(pO₂) - самый «крутой», что обеспечивает значительную отдачу кислорода при небольшом уменьшении рО₂. Отметим, что на крутом участке кривой насыщения миоглобина ниже 5,3 мкм рт. ст. отношение ΔMbO₂/ΔpO₂ также максимально (см. рис. 4.8). Это означает, что при небольшом изменении рО₂ в капилляре гемоглобин отдает значительный объем кислорода, а миоглобин присоединяет и отдает этот объем при незначительном изменении рО₂. «Рабочие» участки на кривых HbO₂ = f(pO₂) и MbO₂ = f(pO₂) согласованы между собою таким образом, что небольшому изменению рО₂ и значительной отдаче О₂ в капилляре соответствует аналогичный феномен на миоглобине - отдача значительного объема О₂ при незначительном изменении рО₂. Изменение переноса кислорода на цитохромоксидазу не вызовет сколько-нибудь существенного уменьшения «рабочей» величины рО₂ и не повлияет на максимальную скорость дыхания. Таким образом, на обеих кривых имеет место оптимальное сопряжение «противоположных» участков, обеспечивающее значительную экономию капилляров и молекул гемоглобина.

Отметим еще одно важное обстоятельство: пространственное распределение митохондрий и миоглобина в кардиомиоците совпадают. Митохондрии в сердечных клетках ориентированы таким образом, что наибольшая концентрация митохондрий приходится на часть клетки, ближнюю к капилляру; по мере удаления от капилляра концентрация митохондрий снижается [277]. Молекулы кислорода с высокими рО₂ поступают из капилляров в «удаленные» митохондрии за счет прямой диффузии, «теряя» при этом часть величины рО₂. Молекулы кислорода с низкими рО₂ транспортируются молекулами миоглобина без потерь рО₂. Таким образом, пространственное распределение митохондрий и миоглобина позволяет

обеспечить оптимальное «качество» кислорода по всему объему кардиомиоцита. Экспериментально показано [354], что миоглобин имеет одинаковую среднюю величину рО₂ в обоих желудочках. Наличие дополнительного миоглобинного переноса кислорода позволяет значительно увеличить скорость диффузии кислорода из капилляров. Если бы не было «ближнего» расположения митохондрий и в кардиомиоцитах отсутствовал миоглобин, для адекватного снабжения клеток кислородом по «качеству» и «количеству» потребовалась бы капиллярная сеть значительно большей плотности.

Рассмотрим объемный состав «противоположностей» - энергопроизводящих и -потребляющих компонентов кардиомиоцита. Согласно экспериментальным данным [304] 34% объема сердечной клетки составляют митохондрии, 48% - миофибрилы, 1,5% - Т-система и ретикулум, 16,5% другие компоненты. Доля «энергопроизводящего» объема клетки близка к «золотой» (38%). Такое соотношение энергопроизводящих и энергопотребляющих субклеточных структур в кардиомиоците позволяет последнему исполнять свою функцию с минимальными затратами энергии и живого вещества. В конечном счете, налицо энергооптимальное сопряжение по объему «производителя» и «потребителя» энергии. Добавим к этому, источник механической энергии – миокард - также составляет 37% от общего объема сердца [194]. Золотое соотношение объемов является общим правилом. Установлено [26], что

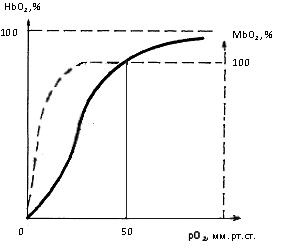
Рис. 4.8. Сопряжение кривых насыщения гемоглобина и миоглобина. Величина 50 мкм мм рт. ст. соответствует рО₂ на артериальном конце сердечного капилляра

реализацию энергетических потребностей организма обеспечивает «золотая» доля его объема (38%); этот показатель сохраняется для различных представителей животного мира, включая и человека. Необходимо добавить к этому, «энергетический заряд» системы АТФ – АДФ – АМФ, характеризующий долю энергии, непосредственно используемой на исполнение биохимических процессов в кардиомиоците, равен 0,611, т.е. близок к числу j=0,618 [199]. Это означает, что «противоположные» мощности в системе АТФ – АДФ – АМФ соотносятся по золотой пропорции.

Важнейшим показателем эффективности деятельности клетки является отношение ее боковой поверхности к объему. Величина этого отношения характеризует уровень обмена клетки с окружающей средой. Кардиомиоцит можно представить в виде кругового цилиндра, где отношение боковой поверхности к объему S/V=4/d (d – диаметр мышечной клетки). Очевидно, чем меньше диаметр клетки, тем большая поверхность приходится на единичный объем и тем выше уровень обмена с окружающей средой. Покажем, что отношение S/V для кардиомиоцита имеет максимальное значение. С этой целью рассмотрим особенности пространственной организации субклеточных структур. Саркомеры являются «силовой» частью миоцитов. В плоскости, перпендикулярной к длине саркомеров, сечения миозиновых нитей располагаются по вершинам равносторонних треугольников, а актиновые - в их центре [273] (см. рис. 4.9). Такой способ упаковки соответствует наиболее плотному равномерному расположению на заданной площади множества одинаковых элементов [170]. Очевидно, что за счет снижения количества саркомеров, как было показано выше, и максимальной плотности их упаковки диаметр кардиомиоцита значительно уменьшается.

Эффективно используют пространство кардиомиоцита и энергопроизводящие структуры кардиомиоцита. В сердечной клетке митохондрии располагаются между миофибриллами, а также под сарколеммой и у полюсов ядер [45]. Количество «сильных» саркомеров в клетке равно минимально возможной величине. Очевидно, что и количество митохондрий, «работающих» к тому же с максимальной скоростью, минимально. За счет экономии митохондрий имеет место дополнительное уменьшение диаметра кардиомицитов.

Рис. 4.9. Взаимное расположение актиновых и миозиновых нитей в поперечном сечении кардиомиоцита. l - миозиновые нити, · - актиновые нити [140].

Отметим «золотые» особенности пространственной организации ядра клетки. Установлено [149], что в поперечном сечении двойная спираль ДНК - правильный пятиугольник. Отношение диаметра и шага спирали ДНК равно 1,602, т. е. практически совпадает с золотым числом 1,618 [34]. Молекула ДНК представляет собой вращающийся куб. При повороте куба последовательно на 72^о по определенной модели получается икосаэдр, который составляет пару додекаэдру, затем опять икосаэдр и т. д. (Заметим, кстати, что структура молекулы миоглобина также имеет форму икосаэдра [89].) Правильные многогранники (куб, икосаэдр, додекаэдр) взаимосвязаны и каждый из них может быть получен путем прямого или косвенного перехода с использованием золотого числа Ф=1,618 [90]. Таким образом, пространственная структура ДНК, так или иначе, связана с платоновыми телами и золотым числом 1,618! К этому следует добавить, что расположение линейных полимеров ДНК по двойной спирали позволяет осуществить их наиболее плотную упаковку и свести к минимуму объем ядра.

В дополнение к вышесказанному, следует указать на «золотые» особенности генетического кода [163]. В 1990 г. французский исследователь Jean-Claude Perez открыл математический закон, управляющий самоорганизацией нуклеотидов Т (тимин), С (цитозин), А (аденин), G (гуанин) внутри ДНК. Он обнаружил, что последовательные множества нуклеотидов ДНК организованы в структуры, называемые резонансами. Резонанс представляет собой особую пропорцию, обеспечивающую разделение молекул ДНК в соответствии с числами Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...) и названную SUPRA-кодом ДНК. По мнению автора открытия, SUPRA-код ДНК является универсальным биоматематическим законом, который указывает на высочайший уровень самоорганизации нуклеотидов в ДНК согласно принципу золотого сечения. Добавим к этому, что все молекулы, входящие в двойную спираль ДНК, имеют «левую» диссимметрию, что в наибольшей степени удовлетворяет требованиям кодирования, хранения и передачи информации.

Итак, максимально плотная упаковка саркомеров, митохондрий, ядра, и, по-видимому, других структур клетки позволяет свести диаметр кардиомиоцита к минимуму. При этом обеспечивается максимум отношения поверхности к объему (S/V=4/d). Добавим, аналогичная картина имеет место и для сердечного капилляра, где отношение S/V также равно максимальной величине.

Аналогия «минимальности» S/V обеспечивает максимальный уровень метаболизма с внешней средой как для крови, так и мышечной ткани. По-видимому, что это отношение отражает оптимальный характер метаболизма между мышечными волокнами и сетью капилляров. Энергооптимальная гармония сопряжения «противоположностей» в параметрах системы «Кардиомиоцит» обеспечивает, с одной стороны, минимум потребления энергии, минимальный объем строительного материала, минимальное потребление кислорода, с другой стороны, максимальный уровень метаболизма. Как следствие, имеет место оптимальное сопряжение «противоположностей»: снабжающей системы «Капилляр» и потребляющей системы «Кардиомиоцит». Добавим, что эта гармония обеспечивается в результате оптимального сопряжения архитектонических, гемодинамических, кислородных параметров капилляров и субклеточных параметров кардиомиоцитов. В конечном счете, вследствие оптимального сопряжения этих факторов объем мышечной массы и плотность капиллярной сети сердца достигают минимально возможной величины.

Заключение

Формально всякая сердечная система, как и любая другая система организма, может иметь множество вариантов конструктивных решений, каждое из которых позволяет этой системе адекватно исполнять заданную ей функцию. Нами показано, любая кардиосистема имеет конструкцию, которая позволяет ей исполнять свою функцию оптимальным образом (с минимальным привлечением энергии и вещества). Можно сделать общее заключение: функции и сложность сердечных систем различны, но принцип их оптимальной энерго- и вещественной организации постоянен. Таким образом, получен ответ на важнейший вопрос: «Почему существует такой тип сопряжения «простых» систем в «сложной» системе, а не какой-либо другой?». Ответ состоит в том, что оптимальный тип сопряжения обеспечивает наиболее «дешевую» работу как отдельных кардиосистем, так и всего органа в целом. Принцип оптимального вхождения утверждает приоритет экономии энергии и вещества, воплощенный в структуре и организации всех сердечных и, по-видимому, других систем организма. Феномен экономии энергии и вещества является общим правилом для кардиосистем всех млекопитающих.

Читатель имел возможность убедиться: во многих сердечных объектах «противоположности» и целое объединяет уникальное математическое выражение - пропорция золотого сечения. Золотым «противоположностям» в структуре важнейших параметров деятельности сердца неизменно сопутствует максимально возможная экономия энергии и вещества. Выявленный феномен экономии позволяет снять давний покров загадочности и таинственности, с которым обычно связывают присутствие золотой пропорции в живой природе. Все очень «просто»: за «удивительными», «загадочными», «таинственными» проявлениями этой пропорции в системах сердца неизменно «скрывается» внутренняя взаимосвязь между золотой гармонией «противоположностей» и минимальным расходом энергии и вещества. Отметим, поиск режима минимальных затрат энергии и вещества для всех систем сердца является приоритетным. Гармония «противоположностей» является своего рода математическим «показателем» оптимальности достигнутого результата.

Следует отметить другие достоинства золотой пропорции. Было показано [217], что в сложных системах, имеющих в основе структуру золотой пропорции, возникает состояние, близкое к резонансу. Подобная связь для сердца теоретически представлена в работе В.Н. Трифанова [172]. Достоинством резонансного режима является минимальный расход энергии, необходимый для поддержания синхронной работы множества связанных систем. При отклонении систем от резонанса нарушается равновесие, возникает необходимость в дополнительных затратах энергии для поддержания устойчивости систем. Резонанс, возникший на уровне «золотой» гармонии «противоположностей», позволяет поддерживать синхронизацию сердечных процессов с минимальными затратами энергии. Можно сказать, сопряжение золотой гармонии «противоположностей» и резонанса – это результат поиска наиболее «дешевого» энерго-вещественного и наиболее устойчивого режима деятельности сердца. Отметим еще одно преимущество, которое обеспечивается золотой гармонией «противоположностей». В статье В.Л. Владимирова и А.П. Стахова [36] представлена связь золотого сечения с информационной энтропией. При этом показано, что именно в точке золотого сечения имеет место максимальная энтропия информации, что обеспечивает системе максимальные информационные возможности. Установлено [74], чем ближе соотношение «противоположностей» к золотому сечению, тем больше появляется свойств у целого, несводимых к свойствам частей. Таким образом, «использование» Природой золотой пропорции позволило создать не только предельно экономный, но и устойчивый орган - сердце, обладающий, к тому же, и большей совокупностью свойств, чем при любой другой, «незолотой», структуре «противоположностей». Можно сказать, золотая пропорция – это гениально простое математическое решение, найденное Природой для наиболее эффективной реализации важнейших требований, предъявляемых к различным аспектам деятельности сердца и, по-видимому, многих других систем организма. «Золотое» сопряжение функции, структуры и организации сердца является ярчайшим примером гармонии живой природы.

Выявление взаимосвязи между гармонией «противоположностей» и принципом оптимального вхождения является, по нашему мнению, еще одним шагом на пути к пониманию проблемы эволюции, одной из сложнейших в биологии. Принцип оптимального вхождения по своему определению («простое» оптимальным образом включается в «сложное») указывает направление эволюции организмов. Механизмом, определяющим сущность эволюции, как нам представляется, является элементарный механизм движения материи (ЭМД), выдвинутый генетиком В.В. Петрашовым [117]. Организм, как убедительно показал Петрашов, в ответ на длительное изменение условий внешней среды стремится к новому состоянию, которое оптимальным образом соответствует изменившимся обстоятельствам. В.И. Коробко [90] установлены многочисленные проявления золотой пропорции в деятельности организма человека: его физиологических ритмах, эргономических параметрах «вхождения» в окружающую среду. По нашему мнению, «золотое» деление допустимых интервалов этих параметров происходит за счет оптимизации «противоположностей» и в «простых», и в «сложных» системах. Совместный процесс эволюции любой «сложной» и образующих ее «простых» систем продолжается вплоть до достижения каждой из них полного энерго-вещественного совершенства.

Представленная нами в 3 и 4 главах книги последовательная «сборка» кислороднесущих и кислородпотребляющих систем сердца является, по нашему мнению, убедительным подтверждением энергооптимальной взаимосвязи принципа оптимального вхождения и элементарного механизма движения материи.

Полученные нами результаты заставляют вспомнить о «мире идей» - учении величайшего философа древности Платона (427-347 до н.э.). Согласно Платону материальный мир, который нас окружает и который мы познаем своими чувствами, является лишь «тенью» и произведен от «мира идей». Идея представляет собой предельное совершенство любой вещи и, как идеал, она оказывается первичной по сущности. Платон был пифагорейцем, его «идеальный» мир основан на математике. Произведенный нами анализ «мира экспериментального» (по Платону - мира вещей) с привлечением «мира математического» (по Платону - мира «идей») позволяет утверждать следующее: Золотая Гармония является «математической идеей» предельного совершенства, воплощенной Природой в сердечных и во многих других биосистемах.

В книге показано, что кровоснабжение сердца в покое основано на золотом сечении. Из житейской практики каждому известно, что после прекращения физической нагрузки кровоснабжение организма и режим работы сердца через некоторое время возвращается в режим физиологического покоя. В покое сердце работает в самом экономичном, «золотом» режиме. Отметим, состояние покоя является преобладающим в жизни даже самых активных животных. Таким образом, в течение большей части жизни кровоснабжение сердца и организма обеспечивается при наиболее экономной, золотой гармонии «противоположностей»! Сопряжение «противоположностей» при внешнем «возмущении» организма (в нашем случае при мышечной нагрузке) связано с отклонениями последних от золотых чисел 0,382 и 0,618. Нами показано, что «отклонение» от золотого сечения при некотором уровне нагрузки соответствует деятельности сердца, наиболее экономной для этого уровня. Таким образом, в пределах нагрузки наряду с классическим золотым сечением отклонения от золотых «противоположностей» составляют «математическую» базу оптимальных режимов работы сердца. Математической основой, представляющей эти соотношения, является выражение:

0,382+0,618/@1.

Этот закон является универсальным основанием гармонии «противоположностей» для всех параметров «пространств» (2.28), (2.72) и (2.78). Он же представляет изоморфию ритмики различных сердечных параметров при любом уровне нагрузки и, по-видимому, при других вариантах градуированных внешних «возмущений». Отметим, представленное соотношение является общим для различных видов млекопитающих и не зависит от веса и размера животных (относительные пределы нагрузки для всех животных опосредованы приблизительно одним и тем же диапазоном безразмерных чисел d=1-4).

Ранее нами было показано [194], что «пространства» (2.28), (2.72) и (2.78) некоторой особи с использованием установленных законов преобразования могут быть «пересчитаны» в аналогичные «пространства» других животных. Операции подобного рода указывают на связь аспектов гармонии и симметрии для различных видов млекопитающих. За счет симметрийных преобразований совместно с золотыми «противоположностями» от одного вида животных к другому происходит «перенос» таких аспектов как высокая экономичность и устойчивость. Золотая гармония «противоположностей», экономичность и устойчивость как бы «тиражируются» на различные виды млекопитающих.

В соответствии с системным подходом Ю.А. Урманцева «пространства» (2.28), (2.72) и (2.78) являются «простыми» элементами сложной системы – «пространства» ССЦ млекопитающих. В свою очередь, это «пространство» в качестве «простого» элемента может входить в еще более сложную систему - «пространство» ССЦ позвоночных. Эта система включает в себя «пространства» ССЦ рыб, земноводных, рептилий, птиц и млекопитающих. Со значительной степенью вероятности можно предположить, что и в «пространствах» ССЦ птиц, рептилий, земноводных и рыб также присутствует энергооптимальная гармония «противоположностей», построенная на золотой пропорции. Как нам представляется, должны существовать законы симметрийного преобразования «сердечных пространств» позвоночных друг в друга. Установление таких законов имело бы большое значение для выявления некоторых новых особенностей систематизации всего сообщества позвоночных. К сожаленью, из-за ограниченности и «мозаичности» экспериментальных данных установление законов композиции и законов преобразования «пространств» ССЦ позвоночных является, по-видимому, делом отдаленного будущего.

Рассмотрим преимущества «использования» золотого сечения для гармоничной связи между сердцем и внешней средой. Нами показано, что сердце - предельно экономный орган как по затратам энергии на обеспечение его функции, так и по объему материала, необходимого для строительства органа и возобновления его структур. Пища, поступающая в организм из внешней среды, является тем источником, из которого клетки сердца и других органов получают энергию и строительный материал. Очевидно, что адекватная жизнедеятельность сердца при «золотой» конструкции последнего обеспечивается минимальной массой пищевых компонентов. При всех других, «незолотых», конструкциях сердца потребление пищи из окружающей среды для аналогичной работы было бы значительно больше. Добавим к этому, сердце не является единственной энергооптимальной системой организма. Многие системы организма человека и животных скомпонованы оптимальным образом по отношению к своей функции [113]. Нами было также показано экономное потребление сердечной мышцей важнейших абиотических веществ (вода, кислород), извлекаемых организмом из внешней среды. Таким образом, конечная «цель» Природы, по нашему мнению, это обеспечить адекватное функционирование организма при минимальном потреблении пищевых и других ресурсов из внешней среды. Можно сказать, «слепая» природа показывает «разумному» человечеству пример экономного использования имеющихся в его распоряжении природных ресурсов! Именно к этому призывает выдающийся философ нашего времени Дарио Салас Соммэр: «Если мы хотим жить в соответствии с высшими моральными правилами, то должны умерить свои запросы» [148, с. 423]. У человечества нет более важной задачи, чтобы сохранить то совершенное, что создала для нас Природа. Истинный гуманизм немыслим без единства человека и природы.

Необходимо отметить еще один аспект золотой гармонии - эстетический. По мнению Г.А. Голицына [48, с. 283], «Золотое сечение является оптимальным…в том смысле, что при восприятии доставляет наблюдателю максимум информации при наименьшей затрате ресурсов. А значит - обеспечивает и максимум эстетического наслаждения». Глаз является частью мозга, вынесенной на периферию. В пределах ясного зрения глазное дно пронизано пропорциями золотого сечения [83, 29]. Отсюда следует вывод, что глаз готовит информацию для мозга в пропорциях и ритмах золотого сечения. Как считает Ф.В. Ковалев, «синхронная их работа, при восприятии и переживании прекрасного и дает человеку ощущение гармонии» [83, с. 36]. Форма, организуемая при помощи пропорции золотого сечения, вызывает впечатление красоты, соразмерности, гармоничности. По мнению И.И. Свентицкого [143], благоприятное эстетическое восприятие (красота) структур и процессов, организованных в пространстве и во времени по золотому сечению, обусловлено их резонансом с сердечной ритмикой. Благодаря положительному эстетическому восприятию происходит неосознанный отбор всего того, что является энергоэкономным, т.е. ощущение гармонии соответствует минимальному расходу энергии. Тем самым, крылатое выражение Ф.М. Достоевского — «Красота спасет мир» — получает энергооптимальное обоснование.

В заключение о Гармонии и Норме, сочетании весьма важном в медицине. В наши дни медицина насчитывает множество разделов и направлений. При этом отсутствуют общие теоретические основы медицинских знаний, которые логически концептуально объединяли бы все частные отрасли медицины. Это в первую очередь относится к понятию «Норма». «Норма» - одно из наиболее общих понятий медицины, тесно связанное с понятием гармонии. Нормой обычно принято считать совокупность среднестатистических значений параметров, которые, как установлено из практики, соответствуют здоровому организму. Большая медицинская энциклопедия определяет норму как «условное обозначение равновесия организма, отдельных его органов и функций в условиях внешней среды» [17, т. 21, с. 138]. В этом определении в общей форме представлена гармония равновесия между организмом и окружающей средой. В более позднем издании БМЭ высказывается представление о норме как «оптимуме функционирования и развития человека» [18, т. 17, с. 196]. При этом под оптимальным функционированием подразумевается гармоническое протекание всех процессов в системе с наиболее возможной слаженностью и эффективностью. По определению академика В.П. Казначеева, «Норма есть биологический оптимум живой системы (Отмечено нами. В.Ц.), т. е. интервал оптимального функционирования живой системы. Этот интервал имеет живые границы, в рамках которых сохраняется оптимальная связь со средой, а также согласованность всех функций организма» [75, с. 102]. Исходя из наших исследований, в согласии с этой дефиницией, мы можем предложить следующее определение нормы: «Норма – это гармония оптимальных значений всех параметров жизнедеятельности организма в покое и допустимых пределах внешних «возмущений».

Исходя из проведенного нами исследования, нормальная деятельность сердца в своей основе имеет гармоническое (оптимальное) сопряжение следующих аспектов:

1) функция сердца как мышечного насоса исполняется с привлечением минимального количества энергии;

2) функция сердца осуществляется при использовании минимального объема крови, мышечного и сосудистого материала;

3) геометрическая и пространственная конструкция гемососудистой системы и мышечной ткани сердца обеспечивает максимальный уровень метаболизма между кровью и кардиомиоцитами.

Читатель мог убедиться, роль золотого сечения и чисел Фибоначчи в организации деятельности сердца исключительно велика. Золотая гармония «противоположностей» в покое и оптимальные преобразования «золотых» отношений при внешнем «возмущении» являются своего рода гарантами нормального функционирования здорового сердца и всей системы кровоснабжения организма. Поистине можно сказать, что золотая гармония составляет основу здоровья человека и млекопитающих! Как нам представляется, при конструировании искусственного сердца необходимо учитывать «золотые» соотношения во временной, механической и объемной структурах сердечных циклов. Такое конструктивное решение позволит в максимально возможной степени приблизиться к естественному кровоснабжению организма.

По нашему глубокому убеждению, золотая гармония «противоположностей» представляет собою один из важнейших, если не самый главный, «математический рецепт» оптимизации живых систем. Интенсивность научного поиска в этом направлении позволяет сделать предположение, что в недалеком будущем будут установлены новые золотые «противоположности» во многих системах организма человека и млекопитающих. Однако уже сейчас можно сказать, «золотая» гармония «противоположностей» является важнейшим фактором оптимального функционирования не только сердечно-сосудистой системы, но и всего организма в целом.

Литература

1. Александр Александрович Любищев. Л., Наука, 1982.

2. Аракелян Г.Б. Фундаментальные безразмерные величины. - Ереван, Изд. АН Арм. ССР, 1981. 157 с.

3. Аракелян Г.Б. Фундаментальная теория ЛМФ. – Ереван, 2007.

4. Аристотель. О частях животных. М.: Биомедгиз, 1937.

5. Ассеев И.А. Экстремальные принципы в естествознании и их философское содержание. Л., Изд-во ЛГУ, 1977.

6. Бабский Е.Б. Методика и некоторые результаты исследования механических процессов сердечной деятельности человека в норме и патологии//Биофизика. 1957. Т. 2. № 1. C. 20-23.

7. Бабский Е.Б., Карпман В.Л. Динамокардиография. – М., Медгиз, 1963. 168 c.

8. Бабский Е.Б., Ульянинский Л.С. Электрическая стимуляция сердца. М., Изд-во АН СССР, 1961. 160 c.

9. Балакшин О.Б. Гармония саморазвития в природе и обществе. Подобие и аналогии. М., Изд-во ЛКИ, 2008. 344 с.

10. Баранцев Р.Г., Калинин О.М. Математика в научной деятельности А.А. Любищева //В кн.: Александр Александрович Любищев. Л.: Наука, 1982. С. 65-81.

11. Барбашина Н.Е., Голубь А.С., Шошенко К.А. Принцип оптимальности в кровеносной системе и данные эксперимента //Математическая конференция биологических процессов (тезисы докладов I конференции). Калининград, 1976. С. 212.

12. Белов Н.В. Очерки по структурной кристаллографии//XIII Минерал. сб. Львов. геол. об-ва, № 16, 1967, с 41.

13. Белянин В.С., Романова Е. Жизнь, молекула воды и золотая пропорция //Наука и жизнь. 2004. № 10.

14. Берестецкий Б.Б., Лифшиц Е.М., Питаевский Л.П. Теоретическая физика. Т. IV. Квантовая электродинамика. М., Наука, 1980.

15. Берталанфи Л. фон. Общая теория систем - критический обзор //Исследования по общей теории систем. - М., Прогресс, 1969. С. 23-82.

16. Блюменфельд Л.А. Проблемы биологической физики. - М., Наука, 1977. 336 с.

17. БМЭ. Т. 13. С. 138. М., Сов. энц., 1961.

18. БМЭ. Т. 17. С. 196. М., Сов. энц., 1981.

19. Богданов А.А. Всеобщая организационная наука (тектология) Ч. 1. – Л., Книга, 1925.

20. Боднар О.Я. Геометрия филлотаксиса//Доклады АН Украины. 1992. № 9. C. 9-14.

21. Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов, Изд. «Свит», 1994.

22. Борн М. Физика в жизни моего поколения. М., Изд. иностр. лит., 1963. 535 с.

23. Бочков В.Г. Принцип оптимальности как основа исследования живых систем и некоторые вопросы их математического описания//Особенности современного научного познания. - Свердловск: УНЦ АН СССР, 1974. С. 161-178.

24. БСЭ. Т. 6. С. 128. М., Сов. энц., 1971.

25. БСЭ. Т. 13. С. 1381. М., Сов. энц., 1973.

26. Бурдаков В.П. Жизнь и старение организмов – комплексный анализ //Вестник РАН. 2001. Т. 71. № 1. С. 32-38.

27. Бутусов К.П. «Золотое сечение» в Солнечной системе//Тр. ВАГО «Проблемы исследования Вселенной, - Л., 1978. Вып. 7. С. 475-499.

28. Варден Б.Л. ван дер. Пробуждающаяся наука. - М., Гос. изд-во Ф-МЛ, 1959. 146 с.

29. Варин В.К., Иванов В.В., Иванов С.В. Золотое сечение как критерий нормы в морфологии человека //Вопросы морфологии XXI века. 2009. Вып. 2. С. 202-203.

30. Васютинский Н. Золотая пропорция. - М., Молодая гвардия, 1990. 238 с.

31. Веденеев Б., Харитонов А. Макроэкономическая индикация экономики по «золотому сечению»//Правила игры. 1995. № 2. С. 58-63.

32. Вейль Г. Симметрия. М., Наука, 1968. 191 с.

33. Вигнер Е. Этюды о симметрии. М., Мир, 1971. 318 с.

34. Виленчик М.М. Биологические основы старения и долголетия. – М., Знание, 1987. 224 с.

35. Винер Н. Динамические системы физики и биологии//Вестн. АН СССР. 1964. № 7. С. 43-45 (перевод статьи в New Scientist, № 375. 1964).

36. Владимиров В.Л., Стахов А.П. Энтропия золотого сечения (раскрыта еще одна тайна золотого сечения) //«Академия Тринитаризма», М., Эл № 77-6567, публ. 16643. 14.07.2011.

37. Вовенко Е.П., Иванов К.П. Перепад напряжения кислорода внутри капилляров скелетной мышцы // ДАН СССР. 1990. Т. 312. № 3. С. 755-758.

38. Вовенко Е.П., Иванов К.П. Продольный градиент напряжения кислорода внутри капилляра коры головного мозга // ДАН СССР. 1997. Т. 353. № 1. С. 121-123.

39. Волохонский А.Г. Генетический код и симметрия//Симметрия в природе. - Л., 1971. С. 371-375.

40. Волошинов А.В. Еще раз о математической традиции красоты //Вопр. философ. 2008. № 3. С. 102-112.

41. Волошинов А.В. Математика и искусство. М., Просвещение. 2000. 399 с.

42. Воробьев Н.Н. Числа Фибоначчи. - М., Наука, 1978. 144 с.

43. Гареев Ф.А. Универсальность принципа синхронизации Гюйгенса и Гармония в Природе //Парапсихология и психофизика. 2000. № 1. С. 22-57.

44. Гика М. Эстетика пропорций в природе и искусстве. - М., Изд. акад. арх., 1936. 236 с.

44а. Гительзон И.И., Нефедов В.П., Самойлов В.А. Культура изолированных органов. – Л., Наука, 1977. 196 с.

45. Глаголева В.В., Чечулин Ю.С. Ультраструктурная организация миокарда // В кн: Физиология кровообращения. Физиология сердца. - Л., Наука, 1980. С. 25-35.

46. Глазер Р. Биология в новом свете. - М., Мир, 1978. 173 с.

47. Глотов В.А. Структурный анализ микрососудистых бифуркаций. - Смоленск, 1995. 178 с.

48. Голицын Г.А. Информация и творчество: на пути к интегральной культуре. М., Русский мир, 1997. 429 с.

49. Голубь А.С. Асимметрия артериальных микрососудистых разветвлений // Физиол. ж. СССР. 1978. Т. 64. № 10. С. 1493-1497.

50. Горбачев В.В. Концепции современного естествознания. М., 2003. 592 с.

51. Гратиа Д. Квазикристаллы//Успехи физических наук. 1988. Т. 156. Вып. 2. С. 347-363.

52. Грим Г.Д. Пропорциональность в архитектуре. - М.-Л., ОНТИ, 1935. 148 с.

53. Грин Н., Стаут У., Тейлор Д. Биология в 3 томах. – М.: Мир, 1990.

54. Данилов А.Д., Слесарев В.И. Аквакоммуникация, аквакультура и неизвестные свойства чистой воды //Материалы международной конференции «Нейробиотелеком 2010», Санкт-Петербург.

55. Джавахишвили Н.А., Комахидзе М.Д. Сосуды сердца. - М., Наука, 1967. 356 c.

56. Дирак П.А.М. Воспоминание о необычной эпохе. Сборник статей. М., Наука, 1990.

57. Дмитриева Н.В. Симметрийный подход к анализу электрокардиограммы //Известия АН СССР, сер. биол. 1989. № 3. С. 450-457.

58. Добрых В.А. Экстрасистолия золотых сечений у больных ишемической болезнью сердца//Физиол. человека. 1994. Т. 20. № 1. С. 165-166.

59. Добрых В.А. Аритмии сердца: симметрия, золотое сечение. Хабаровск, 2011. 136 с.

60. Елецкий А.В., Смирнов Б.М. Фуллерены. Успехи физических наук, 1993, т. 163, № 2.

61. Емельянов-Ярославский Л.Б. О логической структуре некоторого самоорганизующего автомата //Проблемы адаптивного управления. Ростов на Дону, 1974. С. 120-156.

62. Желайтис С., Миронов В. Нужна ли жизни форма?//Знание - сила. 1979. № 12. С. 23-24.

63. Жирков А.М., Голиков А.П., Суббота А.Г., Костенко В.А. Использование элементов математической гармонии для определения артериального давления в различных географических зонах и языковых группах //Вестник Межд. академии наук. 2007. № 1. С. 26-30.

63a. Жирмунский А.В., Кузьмин В.И. Критические уровни в процессах развития биологических систем. - М., Наука, 1982. 178 с.

64. Иванов К.П. Биоэнергетика и температурный гомеостазис. – Л., Наука, 1972. 172с

65. Иванов К.П. Основы энергетики организма. Т. 2. Биологическое окисление и его обеспечение кислородом. Спб., Наука, 1993. 270 с.

66. Иванов К.П. Основы энергетики организма. Т. 3. Современные проблемы, загадки и парадоксы регуляции энергетического баланса. Спб., Наука, 2001. 277 с.

67. Иванов К.П., Кисляков Ю.Я. Энергетические потребности и кислородное обеспечение головного мозга. - Л., Наука, 1979. 214 с.

68. Иванов К.П., Дерий А.Н., Самойлов М.О. Диффузия кислорода из артериол мозга // ДАН СССР. 1979а. Т. 244. № 6. С. 1509-1513.

69. Иванов К.П., Лябах Е.Г. Снабжение кислородом мышцы при полной замене крови кислородпереносящим кровезаменителем //Физиол. ж. СССР. 1980. Т. 66. С. 1695-1701.

70. Иванов К.П., Вовенко Е.П., Дарий А.Н. Напряжение кислорода в мышечных капиллярах и механизмы капиллярного газообмена //ДАН СССР. 1982. Т. 265. № 2. C. 494-497.

71. Иванов К.П., Вовенко Е.П. О специфических особенностях снабжения тканей кислородом из артериол и из капилляров //ДАН СССР. 1986. Т. 286. № 1. С. 227-229.

72. Иванова С.Ф. Об оптимальной геометрии сети кровеносных капилляров// Физиол. ж., 1983. Т. 29. № 3. С. 363-370.

73. Иванус А.И. Код да Винчи в бизнесе или гармоничный менеджемент по Фибоначчи. М., Комкнига, 2006.

74. Иванус А.И. О системообразующих свойствах золотого сечения//Академия тринитаризма. М., Эл. 77-6567, публ.13764, 08.09.2006а.

75. Казначеев В.П., Петленко В.П., Петленко С.В. Этюды интегральной медицины и валеологии. Спб, 1997. 432 с.

76. Каро К., Педли Т., Шротер Р., Сид У. Механика кровообращения. М.: Мир, 1981. 624 с.

77. Кершенгольц Б.М., Чернобривкина Т.Б., Шеин А.И., Хлебный Е.С., Аньшакова В.В. Нелинейная динамика (синергетика) в химических, биологических, биотехнологических системах. Якутск, 2009.

78. Кирьянов Г.С., Яблучанский Н.И., Шляховер И.Н., Рябаева Т.В. Морфометрия сердца в норме. – Киев, Выша школа, 1990. 152 с.

79. Клайн М. Математика. Поиск истины. М., Мир, 1984.

80. Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М., Наука, 1989.

81. Клещев Д.С. Математика гармонии и многообразие Вселенной //Исторические исследования. 2002. № 2.

82. Кнышов Г.В. Концепция спиральной структуры сердца: новый этап в лечении сердечной недостаточности //Здоров`я Украiни. 2005. № 123.

83. Ковалев Ф.В. Золотое сечение в живописи. Киев, Выща школа, 1989. 143 с.

84. Козлов В.И., Тупицин И.О. Микроциркуляция при мышечной деятельности. – М., Физк. и спорт, 1982. 135 с.

85. Козлов В.И., Мельман Е.П., Нейко Е.М., Шутка Б.В. Гистофизиология капилляров. Спб.,- Наука, 1994. 232 с.

86. Колков А.И. Гармония и творчество //Вопросы психологии. 1989. № 1. С. 83-90.

87. Колясников Ю.А. Вода - всему начало. - Магадан, 1995. 56 с.

88. Коржуев П.А. Гемоглобин. М., Наука, 1964.

89. Коробко В.И., Коробко Г.Н. Основы структурной гармонии природных и искусственных систем. – Ставрополь, 1995. 350 с.

90. Коробко В.И. Золотая пропорция: некоторые философские аспекты гармонии. М., Изд-во АСВ, 2000. 208 с.

91. Коробов В.Н., Голубий Е.М. Роль миоглобина в адаптации мышечной системы к физическим нагрузкам и гипоксии //Усп. совр. биол. 1993. Т. 113. Вып. 1. С. 60-70.

92. Куприянов В.В., Караганов Я.Л. Функциональная морфология кровеносных сосудов сердца //Кардиология. 1969. Т. 9. № 6. С. 3-12.

93. Куприянов В.В., Караганов Я.Л., Козлов В.И. Микроциркуляторное русло. – М., Медицина, 1975. 216 с.

94. Куприянов В.В. Спиральное расположение мышечных элементов в стенке кровеносных сосудов и его значение для гемодинамики // Архив АГЭ. 1983. Т. LXXXV. Вып. 9. С. 46-54.

95. Куприянов В.В., Ананин В.Ф. Биомеханика спирального расположения мышечных элементов сосудов и механизмов регуляции при гемодинамике //Архив АГЭ. 1988. Т. XCV. Вып. 12. С. 27-35.

96. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. III. Квантовая механика. Нерелятивистская теория. М., Физматгиз, 1963.

97. Ландсберг Г.С. Оптика. М., Гос. изд-во технико-теоретической литературы, 1957.

98. Лебедев Ю.С. Архитектура и бионика. М., Изд-во литературы по строительству. 1971. 119 с.

99. Ле Корбюзье Ш.Э. Модулор. - М., Стройиздат, 1967. 239 с.

100. Лима-де-Фариа А. Эволюция без отбора. М., Мир, 1991. 455 с.

101. Лосев А.Ф. Античный космос и современная наука. М., 1927.

102. Лосев А.Ф. Пифагореизм//Философская энциклопедия. - М., 1967. Т. 4. С. 260.

103. Любищев А.А. Понятие сравнительной анатомии//Вопросы общей зоологии и медицинской паразитологии. - М., 1962. С. 189-214.

104. Ляпунов А.А. О кибернетических вопросах биологии// Проблемы кибернетики. М., 1972. Вып. 5. С. 5-40.

105. Марутаев М.А. Гармония как закономерность природы. //Золотое сечение. Три взгляда на природу гармонии. - М., Стройиздат, 1990. С. 130-233.

106. Мельхидесек Д. Древняя загадка Цветка Жизни. М., София, 2009. 584 с.

107. Мигдал А.Б. Физика и философия// Вопр. филос., 1990. № 1. С. 29.

108. Моисеев Н.Н. Человек, среда, общество. - М., Наука, 1982. 240 с.

109. Молчанов А.М. Нелинейности в биологии. Пущино, 1992. 221 с.

110. Мопертьюи П. Соотношения между общими принципами покоя и движения// В кн.: Вариационные принципы механики. М., 1959.

111.Мчедлишвили Г.И. Микроциркуляция крови. - Л., Наука, 1989. 295 с.

112. Новикова Е.Б. Нарушение регуляции кровоснабжения при снижении тонуса коронарных сосудов//Вестн. АМН СССР. 1980. Т. 1. С. 76-81

113. Образцов И.Ф., Ханин М.А. Оптимальные биомеханические системы. - М., Медицина, 1989. 271 с.

114. Овчинников Н.Ф. Принципы сохранения. М., Наука, 1966. 329 с.

115. Очинский В.В. Концепции золотой пропорции в естествознании //В сб.: Метафизика, М.: Бином, Лаборатория знаний, 2002, с. 256 – 284.

116. Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М., Мир, 1993.

117. Петрашов В.В. Глаза и мозг эволюции. Новая теория эволюции организмов. – М., 2006. 458 с.

118. Петухов С.В. Биомеханика, бионика и симметрия. - М., Наука, 1981. 240 с.

119. Петухов С.В. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение//Метафизика. Москва, Бином, 2006. С. 216-250.

120. Планк М. Единство физической картины мира. М., Наука, 1966.

121. Платон. Тимей. Полн. Собр. соч., т. 3. М., Мысль, 1994. 656 с.

122. Постолаки А.И. О проявлении «золотого сечения», «чисел Фибоначчи» и «закона филлотаксиса» в природе, строении организма и зубно-челюстной системы человека //Академия Тританиризма, М., № 77-6567, публ. 15452, 05. 08. 2009.

123. И. От существующего к возникающему: время и сложность в физических науках. М., Наука, 1985.

124. Пригожин И., Стенгерс И. Порядок из хаоса. Новый диалог человека с природой. М., Прогресс, 1986. 432 с.

125. Пуанкаре А. О науке. М., Наука, 1990.

126. Радюк М.С. Золотая пропорция в структуре хлоропластов высших растений//Изд. АН СССР. Сер. биол. 1987. № 5. С. 774-777.

127. Рассел Б. История западной философии. Новосибирск, Сибир. унив. изд-во, 2003.

128. Рашевский Н. Модели и математические принципы в биологии// Теоретическая и математическая биология. – М.,: Мир, 1968. С.48-66.

129. Регирер С.А. Некоторые вопросы гидродинамики кровообращения //Гидродинамика кровообращения. - М., Мир, 1971. С. 252-258.

130. Роева Л.А. Течение вязкой крови в изогнутых каналах. Приложение к течению крови в аорте//Усп. физиол. наук. 1980. Т. 11. № 2. C. 121-129.

131. Розен Р. Принцип оптимальности в биологии. М., Мир, 1969. 216 с.

132. Розенов Э.К. О применении закона «золотого деления» к музыке //Изд. Спб Общества муз. собр., 1904 (июнь, июль, август). С. 1-19.

133. Розин Б. Золотое сечение – морфологический закон природы. 2003. http://www.abc-people.com/idea/zolotosech/rozin-ru/txt.htm, http://www.trinitas.ru/rus/doc/0232/012a/02322019.htm

134. Руденко АП. Энергетические аспекты основных закономерностей, причин и движущих сил химической эволюции элементарных открытых каталитических систем. Пущино, НЦБИ АН СССР, 1981. 13 с.

135. Руденко А.П. Самоорганизация и прогрессивная эволюция в природных процессах в аспекте концепции эволюционного катализа// Российский химический журнал. 1995. Т. 39. № 2. С. 55-71.

136. Рыбаков Б.А. Архитектурная математика древнерусских зодчих //Советская археология. 1957. № 1. С. 83-112.

137. Рыбин И.А. Психофизика: Поиск новых подходов//Природа. 1990. № 2. С. 19-25.

138. Сабанеев Л. Этюды Шопена в освещении закона золотого сечения //Искусство. 1925. Т. II. С. 132-145; 1927. Т. II-III. С. 32-56.

139. Савицкий Н.Н. Биофизические основы кровообращения и клинические методы изучения гемодинамики. Л., Медицина, 1974. 311 с.

140. Сальмонович В.С. Сократительный процесс в мускулатуре сердца //В сб.: Физиология кровообращения. Физиология сердца. М., Наука, 1980. С. 134-169.

141. Свентицкий И.И. Закон биоэнергической направленности живых систем живых систем и его приложения //Новые идеи в энергетике. Научные труды. М., ВИЭСХ, 1999. Т. 85. С. 77-107.

142. Свентицкий И.И. Энергосбережение в АПК и энергетическая экстремальность самоорганизации. М., 2007. 464 с.

143. Селье Г. От мечты к открытию. – М., Прогресс, 1987. 367 с.

144. Семенюта Н.Ф. Применение рекуррентных соотношений к анализу электрических цепей //Электрические машины, цепи и системы. Труды Белорус. Ин-та инженеров железнодорожного транспорта. БелИИЖТ, 1971.

145. Сивухин Д.В. Общий курс физики. Оптика. М., Наука, 1980.

146. Симонян К.С. Перитонит. - М., Медицина, 1971. 295 с.

147. Слесарев В.И., Шабров А.В. Диплом № 281 на открытие «Явление аквакоммутации в водосодержащих системах». РАЕН, 23.06.2005, М., приоритет от 15.12.2001.

148. Соколов А.А., Соколов А.Я. Математические закономерности электрических колебаний мозга. - М., Наука, 1976. 97 с.

149. Соммер Дарио Салас. Мораль XXI века. М., Изд. дом «София», 2004. 528 с.

150. Сонин А.С. Постижение совершенства. - М., Знание, 1987. 208 с.

151. Сороко Э.М. Структурная гармония систем. – Минск: Наука и техника, 1984. 264 с.

Золотые сечения, процессы самоорганизации и эволюции систем. Введение в общую теорию гармонии систем. М., URSS, 2006. 263 с.

152. Стайер Л. Биохимия. Т.1. М., Мир, 1984. 168 с.

153. Стахов А.П. Введение в алгометрическую теорию измерения. М., Сов. радио, 1977.

154. Стахов А.П. Алгометрическая теория измерений. – М, Знание, 1979.

155. Стахов А.П. Коды золотой пропорции. - М., Радио и связь, 1984. 365 с.

156. Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи//Доклады АН Украины. 1993. Т. 208. № 7. С. 9-14.

157. Стахов А.П. Гармония Мироздания и золотое сечение: древнейшая парадигма и ее роль в современной науке. 2006, http://www.obretenie.narod.ru/txt/stakhov/harmony2.htm

158. Стахов А.П. Золотое сечение, священная геометрия и математика гармонии //В кн.: Метафизика, М., Бином, 2006. С. 174-215.

159. Стахов А.П. Три «ключевые» проблемы математики на этапе ее зарождения. «Математика Гармонии» как альтернативное направление в развитии математической науки //Филос. сборник АНУ «Totallogy. Постнеклассичнi дослiдження». 2007. № 17/18. С. 273-322.

160. Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. СПб, Питер, 2007.

161. Стахов А.П. Роль «Золотого Сечения» и «Математика Гармонии» в преодолении «стратегических ошибок» в развитии математики //Академия Тринитаризма. М., Эл. № 77-6567, публ.14688, 12.01.2008, http://www.trinitas.ru/rus/doc/0232/004a/02321074.htm.

162. Стахов А.П. Математика Гармонии как «золотая» парадигма современной науки //Академия тринитаризма. М., Эл. № 77-6567, публ.15999, 15.10.2009, http://www.trinitas.ru/rus/doc/0232/009a/02321168.htm

163. Стахов А.П., Райлян И.Г. «Золотая» парадигма: этапы большого пути от Пифагора, Платона и Евклида до «Математики Гармонии» //Академия Тританиризма. М., Эл. № 77-6567, публ. 15615, 26.10.2009, htpp://www.trinitas.ru/rus/0232/004a/02321100.htm

164. Стахов А.П. «Родовые признаки» для обобщенных золотых сечений //Академия тринитаризма, М., Эл. № 77-6567, публ. 17515, 10.06.2012, htpp://www.trinitas.ru/rus/0232/009а/1260-sth.pdf

165. Степанов И.Н. Формы в мире почв. - М., Наука, 1986. 190 с.

166. Суббота А.Г. «Золотое сечение» («sectio aurea») в медицине. - С.-Птб., ИНТФ ИНТФ «Стройлеспечать» 1996. 167 с.

167. Татаренко А.А. На пороге первого тысячелетия эры полигармонии мира// Труды международной конференции «Проблемы Гармонии, Симметрии и Золотого сечения в Природе, Науке и Искусстве». Винница, 2003.

168. Тимеринг Г.Е. Золотое сечение. – Петроград, Научное книгоиздательство, 1924. 86 с.

169. Ткаченко Б.И. Функциональные классификации системы кровоснабжения //Физиол. журн. СССР. 1981. Т. 67. № 1. C. 3-12.

170. Тот Ф.А. Расположение на плоскости, на сфере и в пространстве. - М., Гос. изд-во ФМЛ, 1958. 363 c.

171. Тринчер К.С. Биология и информация. Элементы биологической информатики. М., Наука, 1965. 119 с.

172. Трифанов В.Н. Резонансные основы функциональной гармонии организма // В кн: А.Г. Суббота. Гармония движений, золотое сечение и здоровье. Санкт-Петербург, 2003. с. 124-128.

173. Трифанов В.Н. Резонансная гармония в природе //Гармония и дисгармония в медицине. Вып. 3, Санкт-Петербург, 2004. С. 120-128.

174. Тяпкин А., Шибанов А.. Пуанкаре. М., Мол. Гвардия, 1982. 415 с.

175. Уайдл Д.Дж. Методы поиска экстремума. – М., Наука, 1967.

176. Уайт А., Хандлер П., Смит Е.Л. и др. Основы биохимии. Т. 3. - М., Мир, 1981. 1878 с. 111

177. Углов Ф.Г., Зубцовский В.Н., Большаков О.В. и др. Топография рельефа внутренней поверхности левого желудочка во время диастолы //Арх. анат. 1984. Т. 86. Вып. 9. С.33-41.

178. Уиллер Дж. Предвидение Эйнштейна. М., Мир, 1970.

179. Уотермен т. Заключительное слово// В кн.: Теория систем и биология. М., Мир. 1968 с. 431-442.

180. Урманцев Ю.А. Симметрия природы и природа симметрии. - М., Мысль, 1974. 229 с.

181. Урманцев Ю.А. Что может дать биологу представление объекта как системы в системе объектов того же рода?//Журн. общ. биол. 1978. Т. 39. № 5. C. 699-718.

182. Хаар Д. Тер. Основы гамильтоновой механики. М., Наука, 1974.

183. Хадарцев А.А., Тульян В.А., Зилов В.Г. и др. Теория и практика восстановительной медицины. Тула – Москва, 2004.

184. Хакен Г. Синергетика. М., Мир, 1980.

185. Ханин М.А., Дорфман Н.Л., Бухаров И.Б., Левадный И.Г. Экстремальные принципы в биологии и физиологии. М., Наука, 1978. 256 с.

186. Харитонов А.С. Симметрия хаоса и порядка в круговороте энергии (Холистическая парадигма природы, человека и общества). М., Издательско-аналитический центр «Энергия», 2004.

187. Фейнман Р.П., Лейтон П.В., Сэндс М. М., Фейнманские лекции по физике.

Т. 1. М., Мир, 1965. 267 с.

188. Физиология человека. М., Медицина, 1985.

189. Фолков Б., Нил Э. Кровообращение. - М., Медицина, 1976. 464 с.

190. Цветков В.Д. Ряды Фибоначчи и оптимальная организация сердечной деятельности млекопитающих. – Пущино, НЦБИ АН СССР, 1984a. 19 с.

191. Цветков В.Д. Гемокапиллярное русло млекопитающих и снабжение кислородом миокарда в условиях гипертензии //Арх. анат. 1984б. Т. 86. С. 5-13.

192. Цветков В.Д. Принцип оптимальной конструкции в биосистемах (на примере гемососудистой системы транспорта кислорода сердечной мышцы млекопитающих). – Пущино, НЦБИ АН СССР, 1986. 25 с.

193. Цветков В.Д. Системная организация деятельности сердца млекопитающих. – Пущино, ПНЦ РАН, 1993. 134 с.

194. Цветков В.Д. Сердце, золотое сечение и симметрия. Пущино, ПНЦ РАН, 1997. 170 с.

195. Цветков В.Д. Золотое сечение и гармония сердца //Полигнозис. 1999. № 2. С. 148-155.

196. Цветков В.Д. Биосистемы возрастающей сложности и принцип оптимального вхождения //Полигнозис. 2001. № 2. С. 131-138.

197. Цветков В.Д. Гармония сердца и золотое сечение //В кн.: Проблемы гармонii, симетрii i золотого перетину в природе, науцi та пристецтвi. Винница, 2003. С. 169-175.

198. Цветков В.Д. Кислородное обеспечение сердца и принцип оптимального вхождения. Серпухов, ИП А.А. Кулаков, 2004. 152 с.

199. Цветков В.Д. Пропорция золотого сечения и соотношения аккумуляции

и рассеяния энергии на клеточном уровне //Вестник ВИЭСХ. 2006. Вып. 1(2). С. 196-199.

200. Цветков В.Д. Золотая гармония и сердце. Пущино, ООО «Фотон-век», 2008. 204с

201. Цветков В.Д. Золотая гармония «противоположностей», энергооптимальность и сердце. //Академия Тринитаризма, М., Эл. № 77-6567, публ. 17017, 23.11.2011б. http://www.trinitas.ru/rus/doc/0232/013a/02322044.htm

202. Цветков В.Д. Исследование преимуществ бифуркационного ветвления сосудов докапиллярного участка коронарного русла млекопитающих //Фундаментальные исследования, № 11 (1), 2012, 61-65.

203. Цветков В.Д. Сердце: оптимальные системы транспорта и потребления кислорода. М., УРСС, 2013. 112 с.

204. Церетели Г.В. Метр и ритм в поэме Руставели и вопросы сравнительной версификации//Контекст - 1973: Литературно- теоретические исследования. - М., Наука. 1974. С. 114-137.

205. Черепахин Ю. Г. Парадигма Единой Жизни // «Академия Тринитаризма», М., Эл № 77-6567, публ.15670, 26.11.2009.

206. Чернух А.М., Александров П.Н., Алексеев О.В. Микроциркуляция. – М., Медицина, 1975. 456 с.

207. Черныш П.П. Гармонические соотношения в строении и функции сердечно-сосудистой системы //Ж-л теор. и клинич. медицины. Морфология и физиология. 2000, № 1.

208. Чижевский А.Л. Структурный анализ движущейся крови. – М., Изд-во АН СССР, 1959. 474 с.

209. Шапоренко П.Ф., Лужецкий В.А. Гармоническая соразмерность частей тела человека и принцип обобщенного золотого сечения//Морфология. 1992. Т. 103. № 11-12. С. 122-130.

210. Шевелев И.Ш. Метаязык живой природы. Кострома, издательство «Воскресенье», 2000. 352 с.

211. Шерман И.А. Критерий оптимальности снабжения ткани кислородом и скорости капиллярного кровотока//Физиол. журн. СССР. 1972. Т. 58. № 8. C. 1245-1252.

212. Шестаков В.П. Гармония как эстетическая категория. М., Наука, 1973. 266 с.

213. Шило Н.А., Динков А.В. Фенотипическая система атомов в развитии идей Д.И. Менделеева //Академия Тринитаризма. М., Эл. № 77-6567, публ. 14630. 09.11.2007.

214. Шмидт-Нильсен К. Размеры животных: почему они так важны? М., Мир, 1987. 259 с.

215. Шоу Б. Полное собрание сочинений, т. 6, 1980.

216. Шошенко К.А., Голубь А.С., Брод В.И. и др. Архитектоника кровеносного русла. – Новосибирск, Наука, 1982. 182 с.

217. Шредер М. Фракталы, хаос, степенные ряды. Миниатюры из бесконечного рая. Ижевск: НИЦ «Регуляция и хаотическая динамика», 2005.

218. Щерба М.М. Физиология эритропоэза // В кн.:Физиология системы крови. Л., Наука, 1968. Гл. 4. С. 52-93.

219. Эйген М. Самоорганизация материи и эволюция биологических макромолекул. М., Мир, 1973.

220. Эйген М., Винклер Р. Игра жизни. М., Наука, 1979.

221. Эйзенштейн С.М. О строении вещей.//Искусство кино. 1939. № 6. С. 7-20.

222. Эйнштейн А. Собрание научных трудов в 4-х томах. Т. 4. М.: Наука, 1967.

223. Энгельгардт В.А. Познание явлений жизни.- М., Наука, 1984. 303 с.

224. Якушко С.И. «Фибоначчиева» закономерность в периодической системе элементов Д.И. Менделеева //Академия Тританиризма. М., Эл. № 77-6567, публ.15695. 27.06.2010.

225. Ясинский А.С. Основы унификации элементов математики для инженеров –исследователей и место в нем «золотого сечения» //Академия тринитаризма, М., Эл. № 77-6567, публ. 15365, 26.06. 2009.

226. Altman P.L., Dittmer D.S. Blood and Other Body Fluids. – Washington, D.C.: Federation of American Societies for Experimental Biology, 1961. 539 p.

227. Ashikawa K., Kanatsuka H., Suzuki T., Takishima T. Phasic blood flow velocity pattern in epimyocardial microvessels in the beating canine left ventricle // Circ. Res. 1986. V. 59. № 6. P. 704-711.

228. Bache R.J., Alexander J.A., Rembert Y.C., Greenfield J.C. Coronary hemodynamic responses to paired ventricular stimulation in the awake dog//J. Appl. Physiol. 1970. V. 28. № 2. P. -150.

229. Ball R.M., Bache R.J. Distribution of myocardial blood flow in the exercising dog with restricted coronary artery inflow//Circ. Res. 1976. V. 38. № 2. P. 60-66.

230. Barnard A.C.L., Lopez L., Hellums J.D. Basic theory of blood flow in capillaries // Microvasc. Res.// 1968. V. 1. N. 1. P. 23-34.

231. Barnard R.J., Duncan H.W., Livesay J.J., Buckberg G.D. Coronary vasodilator reserve and flow distribution during near-maximal exercise in dogs // J. Appl. Physiol. 1977. V. 43. № 6. P. 988-992.

232. Bartels H., Harms H. Sauerstoffdissoziationskurven des Blutes von Saugetieren // Pflug. Arch. 1959. Bd. 268. № 4. P. 354-364.

233. Bassingthwaighte J.B., Yipintsoi T., Harvey R.B. Microvasculature of the dog ventricular myocardium // Microvasc. Res. 1974. V. 7. № 2. P. 229-249.

234. Berg V.V. Die Atmung von Herzmuskelschitten der Katze in Abhangigkeit von pH und vom Glucose oder Fructogesatz // Pflug. Arch. 1962. Bd. 274. № 5. S. 480-488.

235. Bergman G. A number system with irrational base //Mathematics Magazine. 1957. N 31. P. 98-119.

236. Bernstein H., Skeleton R.B.T., Irving D.W., Corday E. Myocardial transit time. A new technics for evaluating coronary circulation. I. Effect of systemic pressure//Amer. J. Physiol. 1962. V. 9. №. 5. P. 777-782.

237. Braunwald E., Goldblatt A., Harrison D., Mason D.T. Studies of cardiac dimension in intact anesthetized man. III. Effects of muscular exercise// Circ. Res. 1963. V. 13. N 5. P. 649-655.

238. Breull W., Flor H., Schuchhardt S., Dohm H. Transmural gradients in myocardial metabolic rate // Basic Res. Cardiol. 1981. V. 76. N 5. P. 393-403.

239. Buckberg G.D., Fixler D.E., Archie J.P. et al. Variable effects of heart rate on phasic and regional left ventricular muscle blood flow in anesthetized dogs//Cardiovasc. Res. 1975. V. 9. № 1. P.1-11.

240. Burkhoff D., Sagawa K. Ventricular efficiency predicted by an analitical model//Amer. J. Physiol. 1986. V. 250. R1021-R1027.

241. Canby C.A., Tomanek R.J. Role of lowering arterial pressure of maximal coronary flow with and without regression of cardiac hypertrophy // Amer. J. Physiol. 1989. V. 257. № 4. Pt 2. H1110-H1118.

242. Chien S. Biophysical behavior of red cells in suspensions. - //In: The Red Blood Cell // Ed. D.M.Supergener. V. 11. -N.Y.: Acad. Press. 1975. P. 1033-1131.

243. Cohn D.L. Optimal systems: I. The vascular system // Bull. Math. Biophys. 1954. V. 16. № 1. P. 59-74.

244. Cohn D.L. Optimal systems: II. The vascular system// Bull.Math.Biophys. 1955. V. 17. № 2. P. 219-227.

245. Coulson R.L. Energetics of isovolumic contractions of the isolated rabbit heart//Ann. Rev. Physiol. 1979. V. 41. P. 507-519.

246. Crowell J.W., Smith E.E. Determinant of optimal hematocrit //J.Appl. Physiol. 1967. V. 22. C. 501-504.

247. Duling B.R., Kuchinsky W., Wahl M. Measurements of the perivascular pO₂ in the vinicity of the pial vessels of the cat // Pflug. Arch. 1979. Bd. 383. № 1. S. 29-34.

248. Duling B.R., Klitzman B. Local control of microvascular function: role in tissue oxygen supply//Ann. Rev. Physiol. 1980. V. 42. P. 373-382.

249. Engelking R., Bienroth W. Untersuchungen uber intramuralen Temperaturgradienten des Herzens und seinen Einfluss auf das Elektrokardiogramm // Cardiologia. 1959. Bd. 34. N 3. S. 147-163.

250. Fabel H. Normal and critical O₂-supply of heart // Oxygen transport in blood and tissue. – Stuttgart: Thieme Verlag. 1968. P. 159-171.

251. Fechner G.T. Vorschule der Asthetik. - Leipzig, Breikopf und Hartel, 1897. 264 S.

252. Federspiel W.J., Popel S. A Theoretical Analysis of the Effect of the Particulate Nature of Blood on Oxygen Release in Capillaries // Microvasc. Res. 1986. V. 32. P. 164-189.

253. Feldstein M.I., Henquell I., Honig C. Frequency analysis of coronary intercapillary distances: Site capillary control //Amer. J. Physiol. 1978. V. 235. N 3. H321-325.

254. Fung Y.-Ch.C. Circulation. //In: Biomechanics. N.-Y., Springer Verlag, Berlin-N.Y. 1984. P. 77-166.

255. Gayeski T.E.J., Federspiel W.J., Honig C.R. A grafical analysis of influence of red cell transit time, carrier-free layer thickness, and intracellular pO₂ on blood-tissue O₂ transport //Adv. Exp. Med. and Biol. 1987. P. 25-35.

256. Gayeski T.E.J., Honig C.R. Intracellular pO₂ in individual cardic myocytes in dogs, cats, rabbits, ferrets and rats // Amer. J. Physiol. 1991. V. 260. № 2. Pt. 2. H522-H531.

257. Gazale M.J. Gnomon. From Pharaohs to Fractals. Princenton, New Jersey: Princeton Univercity Press, 1999.

258. Grant C., Bunnell I.L., Green D.G. The reservoir function of the left atrium during ventricular systole//Amer. J. Med. 1964. V. 37. № 1. P. 36-43.

259. Gregg D.E., Fisher I.C. Blood supply to the heart // Handbook of Physiology/Ed/I. Field, Washington // Amer. Physiol. Soc. 1963. P. 1517-1584.

260. Grote J., Thews G. Die Bedingungen fur Sauerstoffversorgung des Herzmuskelgewebes // Pflug. Arch. 1962. Bd. 276. N 2. S. 145-165.

261. Grunewald W., Sowa W. Distribution of myocardial tissue pO₂ in the rat and inhomogeneity of the coronary bed // Pflug. Arch. 1978. Bd. 374. N 1. S. 57-66.

262. Grzedzielski J. Energetyczno-geometryczny kod przyrody. – Warszawa: WarszawskieCentrum studeckiego ruchu naukowego. 1986. 140 p.

263. Hayashida K., Sunagawa K., Noma M., Sugimachi M., Ando H., Nakamura M. Mechanical matcing of the left ventricle with the arterial system in exercising dogs//Circ. Res. 1992. V. 71. N 3. P. 481-489.

264. Henquell L., Honig C.R. O₂ extraction of right and left ventricles // Proc.Soc.Exp.Biol. and Med. 1976. V. 252. N 1. P. 52-53.

265. Hoggat V.E. Jr. Fibonacci and Lukas Numbers. – Boston, MA: Houghton Mifflin, 1969.

266. Holt J.P., Rohde E.A., Peoples S.A., Kines H. Left ventricular function in mammals of greatly different size//Circ. Res. 1962. V. 10. № 4. P. 798-806.

267. Holt J.P., Rohde E.A., Kines H. Ventricular volumes and body weight in mammals//Amer. J. Physiol. 1968. V. 215. № 3. P. 704-715.

268. Honig C.R., Bourdeau-Martini J. Role of O₂ in control capillary reserve //Adv. Exp. Med. Biol. 1973. V. 39. P.55-72.

269. Honig C.R., Gayeski T.E.J. Comparison of intracellular pO₂ and conditions for blood-tissue O₂ transport in heart and working red skeletal muscle //Adv.Exp.Med.Biol. 1987. V. 215. P. 309-321.

270. Hort W. Quantative Untersuchungen uber Capillarisirung des Herzmuskels im Erwachsen – und Greisalter bei Hypertrophie und Hyperplasie//Virh. Arch. 1955. Bd. 327. N 1. S. 5-22.

271. Horwitz L.D., Atkins J.M., Leshin S.V.P. Role of Frank-Starling mechanism of exercise //Circ. Res. 1978.V. 31. N 6. P. 868-875.

272. Huntley H.E. The divine proportions, a study in mathematical beaty. - N.Y.: Dover, 1970. 186 p.

273. Huxley H.E. The mechanism of muscle contraction // Science. 1969. V. 164. P. 1356-1366.

274. Kamiya A., Togawa W. Optimal branching structure of the vascular tree // Bull. Math. Biophys. 1972. V. 34. N 4. P. 431-438.

275. Kamiya A., Togawa T., Yamamoto A. Theoretical relationship between the optimal models of vasculare tree//Bull. Math.Biphys. 1974. V. 36. N 3. P. 311-323.

276. Kappraff J. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong. World Scientific. 2001.

277. Kayar S.R., Banchero N. Distribution of mitochondria relative to capillaries in guinea pig myocardium // Advances in experimental Medicine and Biology. Ed. F.Kreuzer et al. V. 191. - N.Y., Lond.: Plenum Press, 1986. P. 211.

278. Kenner T. On the role of optimization in cardiovascular system//Basic. Res. Cardiol. 1986. V. 81. Suppl. 1. P. 73-78.

279. Khanin M.A., Bucharov I.B. A mathematical model of functional state of the oxygen transport system// Bull. Math. Biol. 1980. V. 42. N 5. P. 627-645.

280. Khouri E.M., Gregg D.E., Rayford C.R. Effect exercise on cardiac output, left coronary flow and myocardial metabolism in unanesthetized dog//Circ. Res. 1965. V. 17. № 5. P. 427-437.

281. Klitzman B., Duling B.R. Microvascular hematocrit // Amer. J. Physiol. 1979. V. 237. P. H481-H490.

282. Lafontant R.R., Feinberg H., Katz L.N. Partition of coronary and cardiac oxygen extraction between coronary sinus and other drainage channels // Circ.Res. 1962. V. 11. N. 4. P. 686-698.

283. Laurent D., Bolene-Williams C., Williams F.L., Katz L.N. Effects of heart rate on coronary flow and cardiac oxygen consumption//Amer. J. Physiol. 1956. V. 185. № 2. P. 355-364.

284. Lenard J.G. A note on form of the erythrocyte //Bull. Math. Biol. 1974. V. 36. N. 1. P. 55-58.

285. Lepeschkin E. Das Elektrokardiogramm. Dresden, Leipzig: Theodor Steinkopff. 1957. 742 S.

285a. Lipowsky H.H., Usami S., Chien S. In vivo measurements of “apparent viscosity” and microvessel hematocrit in the mesentery of the cat// Microvasc.Res. 1980. V. 19. № 3. P. 297-309.

286. Li J.K.-J. A new similarity principle for cardiac energetics //Bull. Math. Biol. 1983. V. 45. № 6. P. 1005-1011.

287. Little W.C., Cheng C.-P. Left ventricular- arterial coupling in conscious dogs//Amer. J. Physiol. 1991. V. 261. № 1. Pt. 2. P. H70-H76.

288. Lowell L.B., Adamson L.S. Relationship between blood flow direction and endothelial cell orientation at arterial branch sites in rabbit and mice //Circ. Res. 1980. V. 48. P. 481-488.

289. Makiguchi M., Kawaguchi H., Tamura M. The effect of intracellular oxygen concentration on ventricular fibrilation //Adv. Exp. Med. and Biol. 1987. V. 215. P. 305-308.

290. Marinelli R., Fűrst B., v. d. Zee H., McGinn A., Marinelli W. The heart is not a pump: a refutation of the pressure propulsion premise of heart function //Frontier Perspectives. 1995. V. 5. N 1. P 15-24.

291. Mochizuki M. On the velocity of oxygen dissociation human hemoglobin and red cell //Jap. Physiol. 1966. V. 16. N 6. P. 649-657.

292. Mochichuki M., Kagawa T. The effect of deoxygenation rate of the erytrocyte on oxygen transport to the cardiac muscle //In: Oxygen transport to tissue. - N.Y & London, Plenum Press. 1973. P. 169-175.

293. Moll W., Bartels H. Oxygen binding in the blood of mammals // Oxygen transport in blood and tissue. Stuttgart, Thime Verlag. 1968. P. 39-47.

294. Monroe R.G. Myocardial oxygen consumption during ventricular contraction and relaxation//Circ. Res. 1964. V. 14. N 4. P. 294-300.

295. Murray C.D. The physiological principle of minimum work: The vascular system and the cost of blood volume//Proc. Nat. Acad. 1926. V. 12. P. 204-214.

296. Myhre E.S.P., Johansen A., Piene H. Optimal matching between canine left ventricle and after load//Amer. J. Physiol. 1988. V. 254. N 6. P. H1051-H1058.

297. Nachev P. The effect of aortic coarctation in concentration of water and electrolytes in cardiac muscles // Proc. Soc. Exp.Biol. 1974. V. 147. N 6. P. H137-H139.

298. Nagy D. Three «Golden Waves»: Social-political and Cultural History of the Gold Section (Glitters in Russian and Ukrainian) //Шлях до гармонии: Мистецтво+Математика. Львiв, Львiвська нацiональна академия мистецтв, 2007, с. 20-74.

299. Needham J. Order and life. - M.I. Press USA, 1968.

300. Nellis S.H., Liedke A.J., Whitesell L. Small coronary vessel pressure and diameter in intact beating rabbit heart using fixed-position and free-motion techniques//Circ. Res. 1981. V. 49. N 2. P. 342-352

301. Niesel W., Thews G., Lubbers D. Die Messung des zeitliche Verlaufes der O₂- Aufsattigung und Einsattigung menschlichen Erythrocyten mit Kurzzeitspectralanalisator // Pflug. Arch. 1959. Bd. 268. S. 296-307.

302. Noordergraaf A., Li J.K.-J., Campbell K.B. Mammalian hemodynamics: a new similarity principle //J. Theor. Biol. 1979. V. 79. № 4. P. 485-489.

303. Olsen Scott. The Golden Section: Nature`s Greatest Secret. New York, Walker Company. 2006. 58 p.

301. Page E., Polimeni P.I., Zak R., Johnson M. Myofibrilar mass in rat and rabbit heart muscle //Circ. Res. 1972. V. 30. N. 4. P. 430-439.

302. Plank M. Religion und Naturwissenschaft. - Leipzig, 1952.

303. Popel A.S. Theory of oxygen transport to tissue // Clin. Rev. Biomed. Eng. 1989. V. 17. P. 257-321.

304. Prothero J. Heart weight as a function of body weight in mammals//Grows. 1979. V. 43. № 3. P. 139-150.

305. Rashevsky N. The principle of adequate design// In: Foundations of Mathematical Biology. Ed. R.Rosen, Academic Press, N.Y. and London. 1973. V. III. P. 143-176.

308. Rayford C.R., Khouri E.M., Lewis F.B., Gregg D.E. Evalution of use of left coronary artery inflow and O₂ content of coronary sinus blood as measure of left ventricular metabolism //J. Appl. Physiol. 1959. V. 14. N. 5. P. 817-822.

310. Reeves W. J., Rakusan K. Myocardial capillary flow pattern as determined by the method of coloured microspheres //In: Oxygen transport to tissue – Eds. M. Mochizuki, C.R. Honig, T. Koyama, T.K. Goldstick and D.F. Bruley, Plenum Press, New York and London. 1988. P. 447-453.

311. Ross G. Blood flow in the right coronary artery dog // Cardivasc. Res. 1967. V. 1. N. 2. P. 138-144.

312. Roy T.K., Popel A.S. Theoretical predictions of end-capillary pO₂ in muscles of athletic and nonathletic animals at VO_2max //Amer. J. Physiol. 1996. V. 271. N 2. P. H721-H737.

313. Rushmer R. F. Constancy of stroke volume in ventricular responses to exertion //Amer. J. Physiol. 1959. V. 196. N 4. P. 745-750.

314. Sallin E.A. Fiber orientation and ejection fraction in the human left ventricle//Biophys. J. 1969. V. 9. № 7. P. 954-964.

315. Santamore Q.P., Carey R., Googrich D., Bowe A.A.// Measurement of left and right ventricular volume from implanted radiopaque markers //Amer. Physiol. 1981. V. 240. N 6. H896-H901.

316. Sarnoff S.J., Braunwald E., Welch G.H. Hemodynamic determinants of oxygen consumption of heart with special reference to tension-time index//Amer. J. Physiol. 1958. V. 192. N 1. P. 148-156.

317. Sasaki Y., Wagner H.N. Measurement of the distribution of cardiac output in anesthetized rats//J. Appl. Physiol. 1971. V. 30. № 6. P. 879-884.

318. Schmidt K., Bickel D., Niesel W. Der zeitliche Verlauf der Sauerstoffabgabe des Blutes an das Herzmuskelgewebe // Pflug. Arch. 1964. Bd. 281. N. 1. S. 79.

319. Schmid-Schonbein H., Rieger H., Fischer T. Blood fluidity as consequence of cell fluidity: flow properties of blood and flow behavior of blood in vascular diseases // Angiology. 1980. V. 31. P. 99-121.

320. Scholtholt J., Lochner W. Systolischer und diastolischer Anteil an Coronarsinusausfluss in Abhängigheit von Grösse der mitleren Ausflusses //Pflüg. Arch. 1966. Bd. 290. N 4. S. 349-361.

321. Schuchhardt S. Myocardial oxygen pressure: mirror of oxygen supply // Adv.in Exptl. Med. and Biol. /Ed. F. Kreuzer et al. - N.Y., Lond. Plenum Press, 1986. V. 191. P. 21-35.

322. Schwarzmann V., Grunewald W.A. Myoglobin-O₂ -saturation profiles in muscle sections of chicken gizzard and the facilitated O₂ transport by Mb // Adv. in Exptl.Med. and Biol. 1978. V. 94. N. 2. P. 301.

323. Seiyama A., Tanaka S., Kosaka H., Shiga T. O₂ transfer from single microvessels to acinar cells in secretin-stimulated pancreas of rat //Amer. J. Physiol. 1996. V. 270. N. 5. Pt. 2. H1704-H1711.

324. Sestier F. J., Meldenberger R.R., Klassen G.A. Role of autoregulation in spatial and temporal perfusion heterogeneity of canine myocardium //Amer. J. Physiol. 1978. V. 235. N. 1. P. H64-H71.

325. Siess M., Stieler K., Leuchtner J. et al. Some problems of cardiac energetics // Basic Res.Cardiol. 1986. Suppl. 1. P. 79-94.

326. Skalak R., Branemark P.-I. Deformation of red cells in capillaries //Science. 1969. V. 164. N. 3880. P. 717-719.

327. Sonnenblick E.H., Downing E.E. Afterload as primary determinant of ventricular performance // Amer. J. Physiol. 1963. V. 204. N 4. P. 604-613.

328. Spinadel W. de. From the Golden Mean to Chaos. Nueva Libreria, 1998.

329. Spiro D., Sonnenblick E.H. Comparison of the ultrastructural basis of the contractile process in heart and skeletal muscle //Circ. Res. 1964. V. 15. Suppl. 2. P. 14-36.

330. Stahl W.R. Similarity and dimensional methods in biology //Science. 1962. V. 137. № 3525. P. 205-212.

331. Stahl W.R. Organ weights in primates and others mammals //Science. 1965. V. 150. №.3699. P. 1039-1042.

332. Stahl W.R. Scaling of respiratory variables in mammals //Appl. Phisiol. 1967. V. 22. № 3. P. 453-460.

333. Stakhov A. The Mathematics of Harmony from Eulicid to Comtemporary and Computer Science. Singapore, World Scientific, 2009.

334. Suga H. Minimal oxygen consumption and optimal contractility of the heart: theoretical approach to principle of physiological control contractility//Bull. Math. Biol. 1979. V. 41. № 2. P.139-150.

335. Sugihara-Seki M., Skalak R. Numeral study of asymmetric flow of red cells in capillaries //Microvasc. Res. 1988. V. 36. N. 1. P. 64-74.

336. Tilton R.G., Williamson R., Murch D.W. Differencies in pericyte contractile function in rat cardiac and skeletal microvasculatures//Microvasc. Res. 1979. V. 18. № 3. P. 325-335.

337. Toborg M. Kenntnis der terminalen Strombahn im Myokard von Ratte und Katze//Z. Zellforsch. 1972. Bd. 23. № 3. S. 369-374.

338.Toma Y., Matsuda Y., Moritani K., Ogawa H. et al. Left atrial filling in normal human subjects : relation between left atrial contraction and atrial early filling//Cardiol. Res. 1987. V. 21. № 4. P.255-259.

339. Tomanec R.J., Palmer P.J., Peiffer G.L. et al. Morphometry of canine coronary arteries, arterioles and capillaries during hypertension and left ventricular hypertrophy//Circ. Res. 1986. V. 58. №. 1. P. 38-46.

340. Thompson D. W. On Grows and Form. Cambridge, 1942. 1116 p.

341. Toyotaka Y., Hiramatsu O., Goto M. et al. Effect of nitroglycerin on diameter and pulsation amplitude of subendocardial arterioles in beating porcine heart//Amer. J. Physiol. 1994. V. 267. № 5. Pt 2. P. H1719-H1725.

342. Tsarikis A.G., Padiyar R., Gordon D.A., Lipton I. Left atrial size and geometry in the intact dog//Amer. J. Physiol. 1977. V. 232. № 2. P. H167-H172.

343. Tsvetkov V.D. Symmetry and organization of the «space» of cardiac cycle structures in mammals. //In: Symmetry of struct. Intern. Symp. Abstracts of pt 2. Budapest, 1989. P. 584 - 587.

344. Tsvetkov V.D. Cardial muscle and the symmetry//In: Fours intern. congr. and exibition of interdisc. study of symmetry. Technion, Haifa, Israel, 1998. P. 142.

345. Tsvetkov.V.D. «Golden» transformations cascade of light energy in plant and animal cells. //In: Intern. Symp.Biological Motility: basic research and practice. Pushchino, 2006. P. 116-117.

346. Valenta J. et al. Biomechanics/ Prague, Academia, 1993. 594 p.

347. Vatner S.F., Higgins C.B., Franclin D., Braunwald E. Role of tachicardia in mediating of coronary hemodinamic response to severe exercise//J. Appl. Physiol. 1972. V. 32. № 3. P. 380-385.

348. Vaupel P. Effect of percental water content in tissues and liquids on the diffusion coefficients of O₂ and CO₂ //Pflug. Arch. 1976. Bd. 361. N. 2. S. 201-204.

349. Vinten-Johansen J., Becker H., Bernard R.J., Buckberg R.G. Differential effects of heart rate on O₂ requirements per beat in working vs non-working canine left ventricles//Fed. Proc. 1980. V. 39. № 3. Pt. 2. P. R1087.

350. Vrettos A.M., Gross D.R. Instantaneous changes in arterial compliance reduce energetic load on left ventricle during systole //Amer. J. Physiol. 1994. V. 267. № 1. Pt 2. P. H24-H32.

351. Weiss H.R., Neuerbauer J.A., Lipp J.A., Sinha A.K. Quantative determination of regional oxygen consumption in the dog heart //Circ. Res. 1978. V. 42. N. 3. P. 394-401.

352. Weiss H.R., Conway R.S. Morphometric study of the total and perfused arteriolar and capillary network of the rabbit left ventricle//Cardiovasc. Res. 1985. V. 19. P. 348-354.

353. Whalen W.J. Intracellular pO₂ in heart and skeletal muscle //Physiologist. 1971. V. 41. N. 2. P. 69-82.

354. Whalen W.J., Nair P., Buerk D. Oxygen tension in the beating cat heart in situ//In: Oxygen supply. Baltimore. - Urban, Schwarzberg. 1973. P. 199-203.

355. Wiedemann M., Tuma R.F., Macrovitz H.N. An introduction to microcirculation. New York; Washington, 1981. 216 p.

356. Yipintsoi T., Scanlon P.D., Bassingthwaighte J.B. Density and water content of dog ventricular myocardium//Proc. Soc. Exper. Biol. Med. 1972. V. 141. N. 3. P. 1032-1035.

357. Zamir M. Optimality principles in arterial branching //J. Theor. Biol. 1976. V.62. N. 1. P. 227-251.

358. Zamir M., Chee H. Branching characteristics of human coronary arteries//Canad. Physiol. 1985. V. 64. P. 661-668.

359. Zeising A. Neue Lehre von den Proportionen des menschlichen Korpers. – Leipzig, R. Weigel. 1854. 457 S.

360. Zeising A. Aesthetische Forschungen. - Frankfurt a. M., Meidinger. 1855. 568 S.

361. Zwehl W., Gueret P., Meerbaum F. S., Holt D., Corday E. Quantitative two dimensional echocardiology during bicycle exercise in normal subjects// Amer. Cardiol. 1981. V. 47. N 4. P. 866-873.

362. Zweifach B.W. 1971 E.M. Landis/ Award acceptance speech //Microvasc. Res. 1971. V. 3. P. 345-353.

The summary

The golden harmony, optimality and heart. New aspects of organization of functioning of human and mammalian heart

Tsvetkov V.D.

This book introdes readers to harmony of heart, one of the most astonishing of nature¢s creations. In all cardiac systems of different complecity and purpose, heart¢s work is based on optimal conjugation (harmony) of the “opposites”.Using systematic analysis experimental results of domestic and foreign researches, autor establishes energy-optimal crireria for harmony of human and mammalian heart – the principle of optimal entry. Accoding to this principle, “every one of “simple” cardiac systems, constituing together a “complex” cardiac system, is optimally included in the complex system, thus making is perfom its function with minimum expenditures of energy and vessel material”. Hence, the foundation of harmony of any cardiac systems, regardless of this systems complexity, is energy-optimal conjuction of its “simple” systems. Each of “simple” systems, which together make “complex” system, has duality of optimal “opposites”, ensuring as a result of the most efficient work of the whole complex system. Energy-optimality of harmony of the “opposites” in many systems is explained by unique mathematical properties of the golden section and the Fibonacci numbers. The Golden harmony of the “opposityies” in a way acts as a “sign” in of highest energy-material “quality” of one or another cardiac system or the whole heart.

This book is intended for speshialists, interested in problems of theoretical biology, biophysics, medical researchers, physiologists.

Об авторе

Цветков Виктор Дмитриевич – кандидат биологических наук, член-корреспондент Международной академии информатизации при ООН, член Международного клуба Золотого Сечения при Международной ассоциации симметрии. Имеет более 70 опубликованных научных работ. Автор монографий: «Системная организация деятельности сердца млекопитающих» (1993), «Сердце, золотое сечение и симметрия» (1997), «Кислородное обеспечение сердца и принцип оптимального вхождения» (2004), «Золотая гармония и сердце» (2008), «Сердце: оптимальные системы транспорта и потребления кислорода» (2013). Впервые установил фундаментальный критерий гармонического сопряжения «простых» и «сложных» сердечных систем человека и млекопитающих – принцип оптимального вхождения. В. Д. Цветковым установлено, что энергооптимальная гармония «противоположностей» является общей основой, заложенной Природой в основу организации сердечных систем. Цветков впервые показал, что оптимальная деятельность сердца обусловлена широким «использованием» в кардиосистемах пропорции золотого сечения и чисел Фибоначчи.

Выпускник радиофакультета Московского авиационного института. Научные интересы: теоретические основы организации деятельности сердца человека и млекопитающих (гармония, симметрия, оптимальность). Адрес электронной почты: v.d.tsvetkov@rambler.ru

Тайна «золотого» сердца

В. Д. ЦВЕТКОВ

СЕРДЦЕ, ЗОЛОТАЯ ГАРМОНИЯ И ОПТИМАЛЬНОСТЬ

В.Д. ЦВЕТКОВ

Пущино 2014

УДК 573.22+599+612.176

Рис. 4.8. Сопряжение кривых насыщения гемоглобина и миоглобина. Величина 50 мкм мм рт. ст. соответствует рО2 на артериальном конце сердечного капилляра

171. Тринчер К.С. Биология и информация. Элементы биологической информатики. М., Наука, 1965. 119 с.

173. Трифанов В.Н. Резонансная гармония в природе //Гармония и дисгармония в медицине. Вып. 3, Санкт-Петербург, 2004. С. 120-128.

174. Тяпкин А., Шибанов А.. Пуанкаре. М., Мол. Гвардия, 1982. 415 с.

257. Gazale M.J. Gnomon. From Pharaohs to Fractals. Princenton, New Jersey: Princeton Univercity Press, 1999.

Рис. 4.8. Сопряжение кривых насыщения гемоглобина и миоглобина. Величина 50 мкм мм рт. ст. соответствует рО₂ на артериальном конце сердечного капилляра