Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 14. -

Вып. 2. - 2015. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/TITL-46.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-46-html/cont.htm

 

УДК 519.21

 

 ОПТИМАЛЬНОЕ ЧИСЛО КАНАЛОВ В ЭКОНОМИЧЕСКИХ СИСТЕМАХ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ

 

Ó 2015 г. Выборнова Е. И.

 

(vibornova.doc)

 

В работе изложен критерий выбора оптимального числа каналов в системах массового обслуживания с неограниченной очередью.  Предлагаемый критерий основан на оптимизации функции доходности системы. Рассматриваются стационарные системы со случайными потоками заявок, подчиняющиеся уравнениям Колмогорова. Разработаны алгоритмы и программы, которые могут быть использованы на практике при разработке рассматриваемых систем массового обслуживания.

Ключевые слова: системы массового обслуживания, оптимальное число каналов, уравнения Колмогорова.

 

Решении экономических задач часто сопровождается задачами связанным с оптимизацией работы систем массового обслуживания (СМО), таких как системы касс в супермаркетах, ж.д.вокзалах, АЗС и т.п.  К одному  из направлений оптимизации относится направление, связанное с выбором конфигурации СМО с точки зрения получения наибольшего экономического эффекта от работы СМО.

         В данной работе предлагается один из подходов к оптимизации работы СМО, основанный на частном случае систем «размножения-гибели» и стационарных уравнениях Колмогорова [1]. Рассматриваются многоканальные СМО с ограниченной очередью с известной интенсивностью поступления заявок   и интенсивностью обслуживания (-время обслуживания заявки одним каналом). Граф системы представлен на рисунке 1. В системе m каналов и n мест в очереди

 

Рисунок 1. Граф многоканальной СМО с очередью

 

Параметры состояний  известны (  в состоянии  система приносит убытки   y.e./час, в состояниях  доход СМО соответственно  y.e./час, ), состояния, характеризующие очередь, убыточны с С/n y.e/час. Если вероятности состояний  определены, то для характеристики экономической эффективности  работы системы за некоторое время  введем функцию

 

.                                                  (1)

 

В соответствии с графом рисунка 1 имеем формулы для вероятностей состояний СМО

 

,

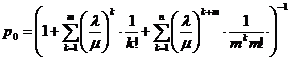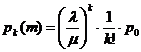
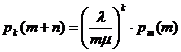.                                                (2)

 

Использование (2) для параметрического анализа  канальной СМО с очередью позволяет исследовать изменение вероятностей состояний  и вероятностей обслуживания заявок  в зависимости от числа каналов обслуживания. Результаты исследования для частного случая приведены на рисунках 2, 3, 4.

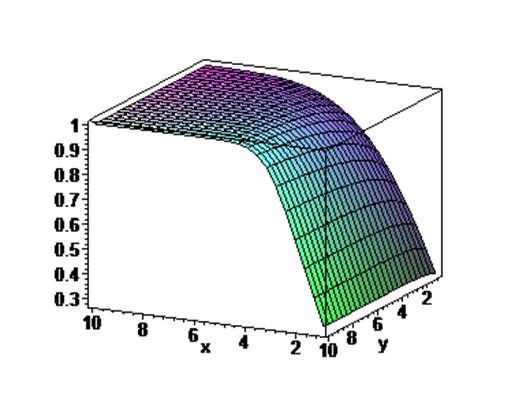
Рисунок 2. Зависимость вероятности обслуживания заявок от числа каналов (x) и числа мест в очереди (y)

 

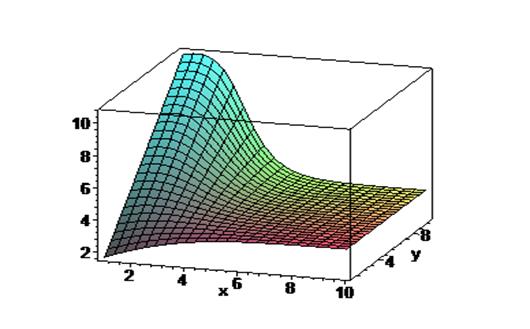
Рисунок 3. Изменение среднего числа заявок в СМО  от числа каналов (x) и числа мест в очереди (y)

 

 

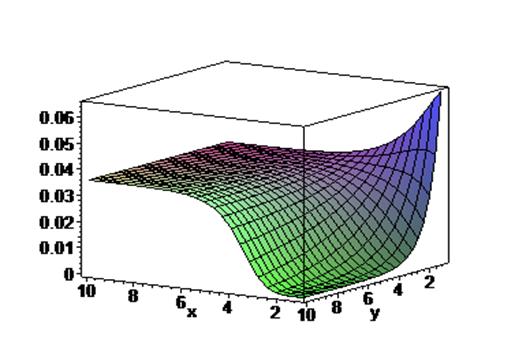
Рисунок 3. Изменение вероятности отсутствия заявок в системе p0  от числа каналов (x) и числа мест в очереди (y)

 

Как и следовало ожидать с увеличением числа каналов вероятность  стремится к постоянной , а вероятность обслуживания поступающих заявок стремится к 1, значит почти все приходящие заявки  будут обслужены. Но среднее число заявок в системе, хотя и изменяется при малом числе каналов обслуживания линейно,  стремится к константе  с ростом числа каналов обслуживания и мест в очереди. Это говорит о том, что увеличивать число каналов обслуживания больше чем некоторое   нет смысла, также как и число мест в очереди, так как с ростом этих чисел убытки будут расти пропорционально этом числам.

         Для выбора оптимального числа каналов исследуем предложенную функцию (1) на экстремум. Параметрическое исследование этой функции представлено на рисунке 5, 6.

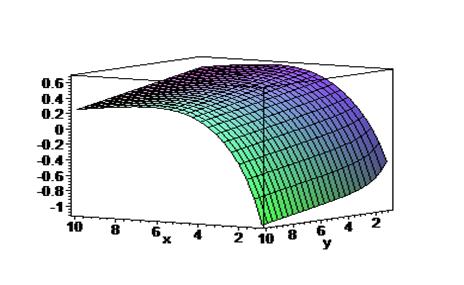
Рисунок 5. Зависимость доходности СМО с очередью от числа каналов обслуживания (ось 0х)  и мест в очереди (y) .

 

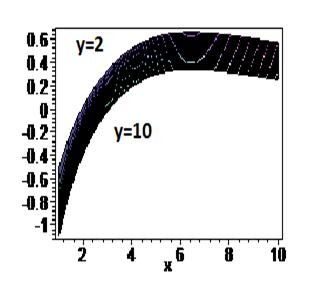
Рисунок 6. Расположение кривых доходности СМО с очередью от числа каналов обслуживания (ось 0х) при фиксации мест в очереди (y)

 

Для параметрического исследования рассматриваемых систем разработана программа в среде MAPLE. Параметрическое исследование показывает:

1.       Существует число каналов обслуживания, при котором функция дохода (1) достигает максимального значения;

2.       Оптимальное число каналов обслуживания, в отличие от случая в [2], смещается в сторону более низких значений с увеличением числа мест в очереди;

3.       С увеличением числа каналов обслуживания и мест в очереди больше некоторого числа М система может стать убыточной.

4.       Результаты исследований и разработанная программа могут быть использованы при выборе конфигурации СМО при создании предприятий малого бизнеса других СМО описываемых рассмотренным в статье графом..

 

Литература

 

1.     Исследование операций в экономике: учебное пособие для вузов по экономическим спец. / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин; под ред. Н. Ш. Кремера . - 2-е изд., перераб. и доп.- М. : Юрайт: Ид Юрайт, 2011. - 430

2.     Денисов В.Н., Лойко Н.В. К выбору оптимального числа каналов в экономических системах массового обслуживания с отказами.- Информационные технологии, энергетика и экономика. ХII международная конференция студентов и аспирантов.

 

THE OPTIMUM NUMBER OF CHANNELS IN THE ECONOMIC SYSTEMS OF MASS SERVICE WITH THE LIMITED QUEUE

 

Vybornova E. I.

 

The paper describes the selection criterion for the optimal number of channels in a Queuing system with limited queue. The proposed criterion based on the optimization function yields the system. Considered the stationary system with random streams of applications, based on the Kolmogorov equations. Developed algorithms and software that can be used in practice in the development of the considered queueing systems.

Key words: Queuing system, the optimal number of channels, Kolmogorov equations.

 

Филиал ГОУ ВПО «Национальный исследовательский университет «МЭИ»

Поступила в редакцию 15.05.2015.