Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 14. -

Вып. 4. - 2015. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-48-html/TITL-48.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-48-html/cont.htm

 

УДК 517.977.5

 

Equivalent substitution in the control theory

 

© 2015 г. Proudnikov I. M.

 

(prudnikov.doc)

 

In this paper a system of the differential equations with a control is considered. We study a problem of looking for an optimal control that gives an infimum for an optimized functional. The system of differential equations is replaced by two systems with the upper and lower envelopes of a function on the right hand side of the initial system of the differential equations. The optimized functional is replaced by its lower envelope. All replacements are done in a region of attainability. The necessary conditions of optimality are sufficient for the substituted system. The rules for evaluation of the attainability set with the help of positively definite functions are given in the second part of the paper.

Key words. Optimal control, optimal trajectories, convex functions, lower and upper convex envelopes, attainability set, convex analysis, linear and convex functions.

 

1  Introduction                                                                     

 

Consider the following general problem of the control theory. Suppose we have a system of the differential equations 

                                                                          (1)

 , and an optimized functional has a form 

                                                                      (2)

 where ,  takes values in , where  is a convex compact set in , . We assume that the function  is continuous and the function  is a Lipschitz one in all arguments in totality, so that the system (1) satisfies the conditions of uniqueness for a solution with the given initial values. We consider the autonomous systems of the differential equations it does not restrict the generality of consideration, as soon as if in the non-autonomous case  is Lipschitz in all arguments uniformly in , then all argumentations, made below, will be true as well.

We have to find an optimal control  that is a piecewise continuously differentiable vector-function from  with values in . We will assume that the derivatives , where they exist, are bounded in the norm, i.e.

                                      

uniformly in . Here  is a set of points in , where the derivatives  exist. In this case pointwise convergence of a sequence  on  is equivalent to uniform convergence of the functions  on a set of continuity and, of course, is equivalent to convergence in the metrics  of the space . The metrics of  is equal, by definition, to the metrics of the space , i.e.

                               

The function  is defined on the segment . We are looking for  for that a solution to the system (1) gives an infimum for the functional .

In the beginning we replace the optimization problem (2) by the following problem 

                                                     (3)

 

Let us include into consideration all the functions  resulting from pointwise convergence. It is obvious that all limit functions belong to a closed, bounded set of functions defined on , which we denote by . The two functions from the set  are equivalent (equal) if these functions are equal on a set of full measure. It is clear that all measurable functions on  belong to .

We will solve the above formulated optimization problem (3) on the set , i.e. 

                                                                              (4)

 

The problem is that an optimal control does not exist always. For this reason generalized control (lower or upper semicontinuous) is considered.

As an example, consider the following system of differential equations

                                         

and the optimized functional is defined as

                            

The similar problem we can in [10] with replacement  on . This problem does not have an optimal control  in the set of piecewise continuously differentiable functions on , but it has an optimizing sequence of controls  that are piecewise continuous functions with values . It is easy to see that an optimizing sequence , corresponding to the sequence of controls , has the limit  on . The control , that corresponds to the solution , can not be received as the pointwise limit of  and it’s not an optimal control.

The right-hand side of the equation (1) can be very complex, and the exact solution of this equation can often be found approximately using numerical methods. Optimization of the function  is also not easy if it has a complex form. But optimization of the lower convex envelope (LCE) of  is easier. Moreover, a global optimum point does not disappear if we construct a lower convex envelope of our optimized functional. In addition, the construction of the lower convex envelope of , that we denote by , turns it into a lower weakly semicontinuous function. It means that

                                        

for any sequence  converging to  weakly. This requirement is important for weak convergence of an optimizing sequence to a solution of the problem (2).

We propose here a method of equivalent substitution with the help of which we can overcome these difficulties. Namely, we suggest a replacement of the right-hand side of the equation (1) by another function with a simpler structure. The search for solutions of the system (1) (numerical or not) becomes simpler. The principle of equivalent replacement claims that although we have another function with a simpler structure, but the function  attains the same infimum on the set of piecewise continuously differentiable functions and on its closure. At the same time the new optimized functional  becomes lower semicontinuous.

This idea is different from the idea of relaxation [1] because we take the convex (concave) envelopes of functions on the right hand side of our system of the differential equations for all points from the region of attainability.

Taking into consideration the information about the replacements of the functions  and , we can conclude that searching for an optimal control and optimal trajectory becomes easier and the new optimization problem is equivalent to the initial one in the sense of finding an optimal control. In this case the conditions of optimality become necessary and sufficient.

For the first time the author used the idea about replacing a function with its lower convex approximation for finding its optimal points in [2] -[3].

 

2   The principle of equivalent replacement

 

Let us consider the same system of differential equations (1), and the optimized functional (4). We rewrite the system (1) and (4) in the following form 

                                                                                  (5)

 with the initial conditions . The optimization problem (4) is replaced by another optimization problem 

                                                                               (6)

 Any solution of (5) is a solution of the integral equations 

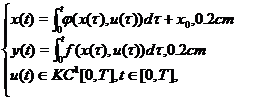                                                             (7)

 where  is a piecewise continuously differentiable control.

Unite all solutions of (7) in one set  for

 

                     

 

                                              (8)

 which is called the set of attainability for the systems (1) and (4) at time .

It is easy to see that the optimization problem (6) is equivalent to the following optimization problem

 

                                                                          (9)

 

The function  is linear in the coordinates . (The function  depends only on the coordinate ). It is well known that any linear function reaches its maximum or minimum on boundary of any compact set on which maximum or minimum are looked for.

Since the set of solutions of (1) in accordance with the assumptions is bounded on , the set of the vector-valued functions  is closed and bounded in . Then  is closed and bounded for any  in the metrics  of the space . Indeed, if , then, as it was mentioned above, there is uniform convergence of  to  on , where  is a set of any small measure. Then convergence in measure [4] holds. The convergences

                         

and

                         

follow from continuity of the functions ,  in all variables.

Uniform convergence of the integrals

                            

and

                           

in  and  follows from Egorov’s theorem [5].

Indeed, otherwise the sequences  and  exist, for that and for some , the inequalities

                         

and

                        

hold. The integrals can be considered as functions of .

According to Egorov’s theorem for any small  there is a set  with measure  , that the integrals, as the functions of , will converge uniformly in  on a set . As soon as the integrals are absolutely continuous in measure, the integrals over the set  with measure  will be arbitrarily small if  is also arbitrarily small. As a result, we come to the contradiction with existence of , for which the inequalities, written above, are true. Thus we have proved the following theorem.

 

Theorem 2.1 The set  is closed and bounded in  for any  in the metrics  of the space .

 

Consider a sequence of the functions defined on , 

                                                                         (10)

 The sequence  converges on  uniformly in , if the sequence  converges in the metrics  to the function  a.e. on . Prove this fact.

Indeed, we know from the said above that the functions  converge to  uniformly on . We replace the control  by the control  in (10). The difference between the original value of the integral (10) and the new value of the same integral can be evaluated in the following way. According to the inequality

             

where  is a Lipschitz constant of the function , the mentioned above difference is arbitrarily small for large  as well. Indeed, we have

          

and the right hand side of this inequality is arbitrary small for large .

We will use the following result.

Lemma 2.1 [6], [7]. The sequence  converges uniformly for  and  to a solution of (1).

 

Summing up everything mentioned above, we can conclude about uniform convergence on  of the solutions  of (1) for  to a solution  of the same system (1) with the control  as .

 

Lemma 2.2 The sequence  defined by (10), converges uniformly on  in  to a solution  of (1). 

 

 

Remark 2.1 Lemma (2.2) is also valid for the case when  in the metrics  of the space , i.e.

                                 

 

 

The problem (9) has a solution if the functional (2) is lower semicontinuous. It will be shown how to make it lower semicontinuous.

If there is a solution to the problem (9) on the set of piecewise continuously differentiable functions , then we have a solution to the problem 

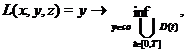                                                                         (11)

 where  is a symbol of taking convex hull.

We introduce a set of attainability (or an attainability set) for the time , which, by definition, is 

                                                                                   (12)

 where  means closed convex hull. It is easy to see that for an arbitrary

                                  

such as

                           

and

                                   

the inclusion

                                       

will be true. Therefore, the closure in (12) can be removed and definition of the set  can be given as the following 

                                                                                    (13)

 Moreover, the problems (9) and (11) are equivalent that means: if one of them has a solution, then the other one has a solution as well and these solutions are equal to each other. In addition, since projections of the set  on the axes  are closed and bounded, and, hence, compact in the corresponding finite-dimensional spaces and  is continuous in  as the set-valued mapping, then  in (11) can be replaced by  and the problem (11) can be rewritten in the following way

 

                                                                                  (14)

 

But a global optimal point of the problem (14) will not change if we replace the functions  by their upper concave and lower convex envelopes and  by its lower convex envelope constructed on a set of attainability for the time . Further we will understand under taking the upper concave and lower convex envelopes of  the similar operations for all coordinates of .

Indeed, take two arbitrary points  and   from the set . Consider a combination with nonnegative coefficients , , . Then, the point  will belong to the set , if we replace the functions  and  by the following:

          

and

         

But this construction, performed for all points of the regions  it just means that we construct the lower and upper convex envelopes of the function  and the lower convex envelope of the functions  in the attainability set for the time , i.e. in . Indeed, it follows from the above formula (13) for  that the function  reaches its minimum (14) on some . Consequently, we can construct the lower convex or upper concave envelopes of the functions  and  in all region .

Denoted by  a new optimization function obtained after the replacement of the function  by  in  

                                    

It is clear that  takes the same optimal value in the attainability set , that the functional   takes for the system (1).

Replace the system  by the system 

                                                                    (15)

 and the optimized functional by the functional

 

                                                                          (16)

 

It is easy to see that the minimum or the maximum of the functional  did not change. Hence, the problems ,  and ,  are replaceable. So "convexification"  of the function , in contrast to the procedure of "convexification" of the function  should be as following: 

    1.  Construction of the lower convex envelope (LCE) of the function  in the variables  for each  from the attainability set for the time , i.e. , which we denote by . LCE of  is the biggest convex function that does not exceed  in .

    2.  Construction of the upper concave envelope (UCE) of the function  (or, equivalently, we construct the lower convex envelope for the function  and after that take minus of this function) in the variables  for each  from the attainability set for the time , i.e. , which we denote by . UCE of  is the smallest concave function that is not less  in .

    3.  Let us replace the system ,  by two systems of the equations: 

                                                  (17)

 with the optimization function  and 

                                                  (18)

 with the same optimization function ;

    4.  Let us find among the solutions of  and  such that gives the smallest value of the functional  in .

 We obtain the following result.

Theorem 2.2 There are the solutions among the solutions of  and  such that deliver a minimum (maximum) in  and  for the functional

                                    

 

that coincides with an infimum (supremum) of the functional  (see (4)). Moreover, necessary conditions for the minimum (maximum) are also sufficient conditions.

 

 

Remark 2.2 The set  is not necessarily compact, although its projections on the axis  are compact . That’s why we are able to go to the problem

                                       

 

if the problem (9) has a solution. The last one coincides with the formulation of Mazur’s theorem. It asserts that in any weakly convergent sequence ,  a subsequence can be chosen for each  convex hull of which is almost everywhere on  converges as  to some . In our case, there exists a sequence , the convex hull of which will converge to an optimal control . The sequence of the solutions , corresponding to the controls , will converge to an optimal solution , corresponding to the control , provided that the solutions have been calculated to the problems with the modified right-hand side.

 

Remark 2.3 The rules for construction of LCE and UCE are given in Appendix.

 

Remark 2.4 In many cases we have to construct only LCE or UCE for the function .

 

Return back to the initial problem (2) with the fixed time . Consider a set

                     

 

                    

 

that is called the set of attainability of the system (1),(2) at time .

Let us introduce a set of attainability for the time  for the system (1),(2) that is by definition 

                                                                                   (19)

 

As above it is possible to prove that we can remove the closure in (19) and write

                                        

 

The optimization problem can be reformulated in the form

 

                                                                  (20)

 

The problems (1), (2) and (20) are equivalent which means if one has a solution, then another one has a solution and these solutions are the same. Moreover, as soon as the projections of the sets  on the axes  are closed, bounded and continuous as a set valued mappings, then we can write instead of   if a solution of (20) exists.

We come to the following result.

Theorem 2.3 There are some solutions among the solutions of  and  such that deliver a minimum (maximum) in  and  to the functional

                                    

that coincides with an infimum (supremum) of the functional  (see (2)) where .is LCE of the function  Moreover, the necessary conditions for minimum (maximum) are also the sufficient conditions.

 

Consider some examples. It is clear that an equivalent replacement of one system by another can be applied to a differential system without control .

Example 1. Consider the differential equation

                             

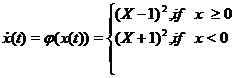
with the initial condition . The optimized functional is given by

                         

The general solution of the differential equations for  has the form

                                          

which tends to  as . The general solution of the differential equation for  is given by

                                          

which tends to  as . In order to meet the initial condition we have to put . The projection of the attainability set  on  axis is the interval

It is clear that the function  takes its minimum at . But we get the same solution if instead of the function  we take its lower convex envelope, namely, the function

                                   

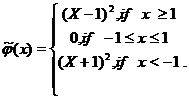
Example 2. The same example, but

                                        

which we minimize for . The equation of the solution is

                                          

Here the replacement of the function  by the function  on the whole line is not correct, since the projection of the attainability set  on  axis is the interval .

Example 3. Let us give the differential equation

                                               

with the initial condition . The general solution has the form

                                            

a solution, satisfying the initial condition, is

                                            

The optimized functional has the form

                                 

for .

It is easy to compute its optimal value

                

In this case, the projection of the attainability set  on  axis is the set . It is easy to see that the lower convex envelope of the functional  on , which we denote by , takes the same infimum value. It is also true for the functional

              

Example 4. Let us consider the following problem

                                  

The optimized functional is

                               

We will get the following system after construction of the lower and upper envelopes

                                        

and

                                      

The optimal solution exists among their solutions .

Example 5. Let us consider the differential equation

                                            

with the initial condition . We are considering piecewise continuously differentiable functions  on the segment  for such that delivers minimum to the functional

                                          

The solution when  is constant on the segment  is given by the form

                                        

Here the constant  is defined by the initial conditions. We can see from here that if  is not constant on , then  for any initial conditions. It means that a curve  will be in a set bounded by the lines  on the plane , where . The set of attainability  will belong to the same set. UCE of the function  in  is a function the graph of which goes through the point . Therefore, if we solve the differential equations with the right sides  and , then among the solutions there are such that deliver the minimum  to the functional  i.e. the formulated theorem is true.

 

3   An evaluation of the attainability set

 

Let us have a system of differential equations 

                                                    (21)

 with the initial condition , where  is Lipschitz in the variables ,  is a convex compact set in . The problem is to estimate the attainability set. By definition, the area of attainability for the time  is the set

 

                                        

where

       

The choice of the initial position and the initial time of zero is not a loss of generality.

Take an arbitrary positively definite function  (see [8]), satisfying the condition

                                    

Let

                                

 

and  is a piecewise continuous vector-function.

Consider the systems of differential equations 

                                                       (22)

 and 

                                                      (23)

 

We denote by 

                                                                        (24)

 

the attainability sets for the systems (22), (23), where

 

                 

 

                                                                              (25)

 

Let the estimates of the attainability sets for the time  be given respectively by the inequalities

                                   

 

We get the estimation for the attainability set of the system (21) for the time . We show that the attainability set  for this system satisfies the inclusion

                                          

Indeed, by definition, the set  will consist of the points on the curves the tangents to which are the sum of the tangents to the curves consisting of the points of the sets  and  for all . It is clear, that for some vector-function  the resulting set will include , which consists of the points on the curves the tangents to which are the sum of the tangents to the curves consisting of the points of the sets  and  for all .

As a result, the following theorem is proved.

Theorem 3.1 For the attainability set  of (21) the inclusion

                                          

is true for some vector-function , where ,  are given by (24), (25) .

 

The following lemma follows from here.

 

Lemma 3.1 The function  satisfies the inequality

                                          

in the attainability set  of the system (21).

 

Now consider two differential systems with the right sides ,  and zero initial conditions at the time equaled to zero.

Let us suppose that the inequality 

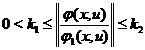                                                                                  (26)

 is true for all . We assume that we know the attainability set  for the time  of the system with the right hand side . The problem is to obtain some estimates of the attainability set of the system (21). The arguments will be carried out as previously, considering the trajectories of the corresponding systems.

Any vector in the set  for some  and  is

                                   

Consequently,

                      

 

                               

Since the previous inclusion holds for any , it follows that

             

The following theorem is proved.

Theorem 3.2 For the systems (21) and (23) with the attainability sets  and  respectively, for which the inequality (28) holds, the inclusion

                                             

is true.

 From here we can easily obtain the following conclusion.

Lemma 3.2 In the attainability set  of the system (21) the function  satisfies the inequality

                                           

where the constant  limits the top value of the function  in the attainability set  of the system (23).

 

Let us give a general method for evaluation of  of the system (21). This method does not require any additional information for the system (21).

As is known, a convex set can be given by its extreme points. There are no problems if there is a finite number of such points. But very often these points are unknown or their number is infinite. We can reconstruct a convex set if we know its projections on different directions. If we project any trajectory, then we project not only the points but the tangents constructed at these points. It means that we have to consider the following system for any direction  

              

As a result, we have 

                                      (27)

 where  is the scalar production .

We can do an orthogonal transformation that the direction of the vector  was the first coordinate axis . Then the projection of the velocity vector  on the line  will be equal to . It means that we have to substitute  into the first equation and to solve the first order differential equation for different values of the constants  that are corresponding coordinates of the start point.

We can make the following conclusion:  convex hull of the attainability sets of the equation (27) for different  will include the attainability set of the equation (21). It is possible to do, because calculation methods are developed very well for the first order differential equations.

 

4  Conclusion

 

The obtained results allow us to pass from local to global optimization problem. To implement this it is required to construct the lower convex and upper concave envelops of the function written on the right hand side of the differential system (1). We also construct the lower convex envelops for the optimized functional. All constructions are done in the attainability set for the time .

A method for estimation of the attainability set with the help of the positively definite functions (Lyapunov functions) is suggested. The proposed method is based on the decomposition of the function, stayed on the right hand side of the system of the differential equations, into the components the sets of attainability of which are already known. It makes it different from the paper [9], where the linear systems are considered.

It is suggested to find projections of  onto any direction . For this reason we have to find projections of the trajectories of the differential system and the tangents to them to the direction . We come across the problem of definition of a set of attainability for the differential equation of the first order.

The proposed transformation method of the systems is especially useful when it is difficult to get a solution of differential equations in an explicit form, but while using approximate methods only. In addition, the sufficient conditions of optimality for an optimal control are obtained according to the proposed method.

 

  APPENDIX

 

We will prove a theorem giving a rule for construction of LCE and UCE.

Let  be continuous function on a convex compact set . It is required to construct LCE and UCE in . Consider a function  

                                

where  is a distribution function satisfying the following equalities 

                               (28)

 

We will consider the functions  for different distributions .

 

Theorem 4.1 The functions

                          

are UCE and LCE of  on  correspondingly.

  Proof. Without loss of generality we will consider that  for all . Divide  into subsets  , . We can approximate the function  with any precision by the integral sums 

                                                                                        (29)

 where

                              

It follows from (28) that 

                                                                               (30)

 The sign  means that the values on the left hand side from this sign can be close to the values on the right hand side with any precision depending on . The expression (29) means that we take a convex hull of  vectors  with coefficients , i.e. we calculate a vector

                              

and define a value of the function  at this point equaled to

                                          

Changing the points  and the coefficients  satisfying (30), we define in such way the functions  with different values at .

Let us prove that the function

                                         

is LCE. As soon as  is taken for all distributions , then the inequality  is true for all . The function  can be approached by the sums (29) for any distribution  under conditions on the coefficients (30). It follows from here that  can not be smaller than LCE of . The operation  keeps this quality. Consequently,  is LCE of . We can prove in the same way that  is UCE of . The Theorem is proved. ∆

The construction of LCE can be done using Fenchel-Morrey’s theorem [10]. According to it LCE is equal to the second conjugate function . Construction of  is not easy. To find a value of LCE at one point we have to solve two difficult optimization problems, namely,

                                  

and

                               

 

 

References

 

[1]  Cesary L. Optimization  Theory and Application. Springer-Verlag, New York, 1983. V. 17. 542 p.

 

[2]   Proudnikov I.M.  The lower convex approximations for Lipschitz functions // J.Comp. Math. and Mathematical Physics. 2000. T. 40. N 3. P. 378-386.

 

[3]   Proudnikov I.M.  The rules for constructions of lower convex approximations for convex functions // J.Comp. Math. and Mathematical Physics. 2003. T. 43. N 7. P. 939-950.

 

[4]  Kolmogorov A.N., Fomin S.V. Elements function theory and functional analysis. Moscow: Nauka, 1976.

 

[5]  Vulich B.Z. A short course in the theory of functions of real variable. Moscow: Nauka, 1973.

 

[6]  Tricomi F.G. Integral equations. Springer-Verlag, 1986.

 

[7]  Krasnov M.L. Integral Equations. Moscow: Nauka, 1976. 217 p.

 

[8]  Zubov V.I., Lectures in control theory. M: Science, 1975. 496 p.

 

[9]  Kostousova E.K. External and internal evaluation of the attainability set with help of the parallelotopics // Computational technology. In 1998. Number 2. T. 3. S. 11 - 20.

 

[10]  Alekseev V.M., Tichomirov V.M., Fomin S.V. Optimal control. M.: Nauka, 1979. 224 p.

 

Эквивалентная замена в задачах оптимального управления

 

Прудников И. М.

 

В работе изучается задача поиска оптимального управления, заданная в виде системы дифференциальных уравнений и оптимизируемого функционала. Определяется правило эквивалентной замены одной задачи оптимального управления на другую с тем же значением оптимального решения. При этом эквивалентная замена определяется таким образом, чтобы условия оптимальности были бы также достаточными условиями. Во второй части статьи даются методы оценки области достижимости, в которой как раз и происходит экви­ва­­лентная замена систем.

Ключевые слова: Оптимизационные задачи, оптимальное управление, оптимальные траектории, выпуклые функции, нижние выпуклые огибающие (НВО), верхние выпуклые огибающие (ВВО), оценка области достижимости.

 

Прудников Игорь Михайлович, к.ф.-м.н., доцент.

pim 10@hotmail.com, ph.num. +79203011393

 

ООО «Научно-исследовательский центр перспективных фундаментальных биотехнологий»

Поступила в редакцию 26.11.2015.