Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 14. -

Вып. 4. - 2015. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-48-html/TITL-48.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-48-html/cont.htm

УДК 623.4

ПОВЫШЕНИЕ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ АКТИВНОГО РАДАРА С СИГНАЛОМ ЕДИНИЧНОЙ БАЗЫ

МЕТОДОМ ИНВЕРСНОЙ ФИЛЬТРАЦИИ

Ó 2015 г. Семченков С. М., Савицкий Ф. Л., Абраменков А. В., Азерский М. А.

(semchenkov-2.doc)

В статье рассмотрены особенности приложения инверсной фильтрации к повышению разрешающей способности активного радара с сигналом единичной базы при воздействии нормально распределенного шума ОСШ от 18 дБ. Получено аналитическое описание отклика инверсного фильтра на такой сигнал во временной области. Указано, что при ОСШ 36 дБ и выше инверсная фильтрация может применятся без дополнительных способов обработки. Для того, чтобы отклик инверсного фильтра был устойчив и позволял разрешать импульсы при ОСШ ниже 36 дБ предложен способ ограничения спектра ожидаемого сигнала снизу. Приведены результаты моделирования обработки данным способом одного, двух и трех импульсов при ОСШ 18–30 дБ. Полученные результаты подтвердили возможность приложения инверсной фильтрации к повышению разрешающей способности схемы обработки импульсного сигнала единичной базы при реально достижимом ОСШ.

Ключевые слова: сигнал единичной базы, разрешение, сверхразрешение, инверсная фильтрация, согласованная обработка.

Для активных радаров с сигналом единичной базы известно противоречием между требованиями к дальности действия и разрешающей способности по дальности. Преодоление данного противоречия требует разработки новых способов и методов обработки сигналов, обладающих лучшими показателями в разрешающей способности по сравнению с традиционными. Так разработаны способы сверхразрешения в методах теорий современного спектрального анализа [7], многоканального анализа [3], многосигнальной радиолокации [1], проекционной теории [8] и других.

Одним из широко применяемых сегодня методов восстановления искаженных сигналов в оптике, цифровой обработке сигналов и других областях радиотехники является инверсная фильтрация [4]. Приложения инверсной фильтрации к повышению разрешающей способности активного радара с сигналом единичной базы в известных работах рассмотрены не были. В настоящей статье оцениваются возможности инверсной фильтрации в повышении разрешающей способности активного радара с сигналом единичной базы и ставиться целью доказать возможность приложения инверсной фильтрации к разрешению произвольного количества импульсных сигналов с неизвестными амплитудой, начальной фазой, временем прихода при реально достижимых отношениях сигнал-шум (ОСШ).

При проведении исследований инверсная фильтрация реализовывалась обработкой сигнала в следующей последовательности:

путем выполнения дискретного преобразования Фурье (ДПФ) над опорным сигналом (копией зондирующего на нулевой дальности) рассчитывался спектр ожидаемого сигнала;

рассчитывался инверсный спектр ожидаемого сигнала, который записывался в память и использовался без изменений при дальнейшей обработке;

выполнялось ДПФ над входным сигналом, формировался его спектр;

спектр входного сигнала перемножался с инверсным спектром опорного сигнала (копией зондирующего);

после перемножения спектров выполнялась операция обратного ДПФ (ОДПФ), вычислялся выходной сигнал схемы обработки.

В результате описанных операций формировался отклик инверсного фильтра на входной сигнал. Характеристика такого фильтра также, как и оптимального определяется видом ожидаемого сигнала и его параметрами.

Ожидаемый сигнал (дискретная копия зондирующего) типа простой (гладкий) радиоимпульс описывается выражением

,

где s – номер дискретного отсчета; S – число отсчетов в импульсе; f₀ – частота; ΔT – интервал дискретизации. Спектральная составляющая с номером n сигнала (1) имеет вид

.

Обозначим в . Величина X в этом случае представляет собой нормированную к интервалу дискретизации частоту, выраженную в долях ширины фильтра. С учетом сделанной подстановки выражение будет выглядеть как

.

Это выражение представляет собой сумму S членов геометрической прогрессии [6], знаменатель которой равен

.

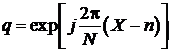С учетом (3), согласно [6] выражение можно привести к виду

,

где .

В выражениях , величина описывает характеристику частотного фильтра с номером n на частоте X. Выражение представляет собой огибающую оптимального фильтра сигнала простого радиоимпульса. Согласно [4] спектр инверсного фильтра является обратным по отношению к и формируется согласно выражению

.

Выражение, описывающее сигнал, образованный несколькими импульсами с различными временами запаздывания имеет вид

,

где М – число импульсов; – комплексная амплитуда m-го импульса; t_Зm – время запаздывания m-го импульса относительно начала отсчета; n_m – номер дискретного отсчета дальности, в котором начинается m-й импульс. Допустим, что интервал дискретизации АЦП ΔT много меньше длительности импульса и по этой причине отдельные импульсы начинаются в разных дискретах дальности.

Комплексная амплитуда спектральной составляющей с номером n сигнала описывается выражением

.

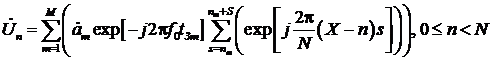После выполнения необходимых преобразований выражение (9) примет вид

,

где .

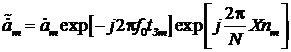Перемножение спектра сигнала с инверсным спектром приводит к результату

.

Выражение (11) представляет собой сумму гармонических сигналов, частоты которых определяются номерами дискрет дальности , в которых начинаются сигналы каждого из М импульсов. Причем все М гармонических сигналов ортогональны друг другу, поскольку величины и являются целыми числами [6]. Это указывает на возможность разрешения всех сигналов независимо от степени их взаимного перекрытия. Покажем это аналитически, записав выражение для ОДПФ над последовательностью .

.

После преобразований выражение принимает вид

,

где .

Поскольку s и n_m целые, выражения и будут равны нулю для всех значений s за исключением s=. Для этих значений s выражение представляет собой известную неопределенность вида 0/0, которая при раскрытии ее по правилу Лопиталя [6] равна N.

Сказанное выше доказывает, что обработка сигнала единичной базы методом инверсной фильтрации позволяет «сжать» простой радиоимпульс до длительности одной дискреты и разрешить перекрывающиеся сигналы. Следовательно, разрешающая способность по дальности простого радиоимпульса при прочих равных условиях определяется только интервалом его дискретизации. Аналогичные выводы о предельной разрешающей способности простого радиоимпульса, полученные другими методами содержится в [2, 5] и других работах, что подтверждает справедливость результатов, изложенных в настоящей статье.

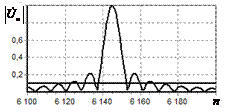
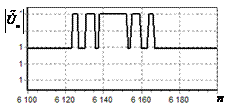
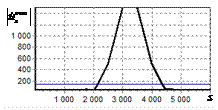
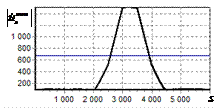
На рис. 1, а показана огибающая амплитудно-частотного спектра (АЧС) простого радиоимпульса. По горизонтальной оси отложены номера спектральных составляющих, по вертикальной – нормированная амплитуда. На рис. 1, б показана огибающая спектра этого импульса после инверсной фильтрации. Из рисунка видно, что модуль спектра постоянен.

а	б
Рис. 1. АЧС простого радиоимпульса до и после инверсной фильтрации а – огибающая АЧС простого радиоимпульса на входе схемы обработки; б – огибающая АЧС радиоимпульса после инверсной фильтрации

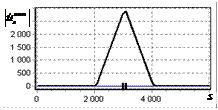
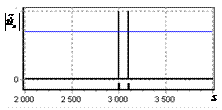
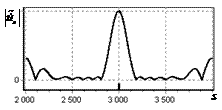
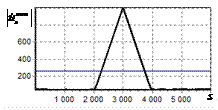
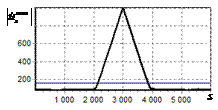
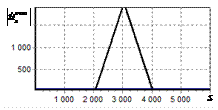
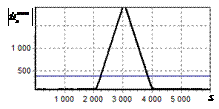
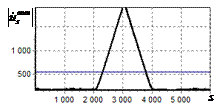
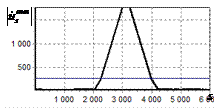
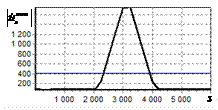
На рис. 2, а показана огибающая простого радиоимпульса на выходе оптимального фильтра. Истинное положение сигнала показано риской на горизонтальной оси. Длительность сигнала задавалась равной 1000 отсчетов АЦП. Огибающая сигнала имеет классический треугольный вид. Протяженность основания огибающей составляет 2000 дискретных отсчетов.

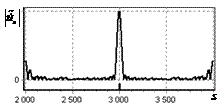
На рис. 2, б показан выходной сигнал инверсного фильтра (после выполнения ОДПФ над инвертированным спектром). Видно, что протяженная огибающая трансформировалась в один пик.

а	б
Рис. 2. Огибающая одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра

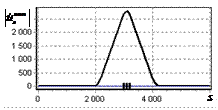
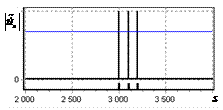
На рис. 3 показаны огибающие сигнала с выхода оптимального фильтра, образованного двумя перекрывающимися импульсами. Фронты импульсов отличаются по времени запаздывания на 100 дискретных отсчетов (величина рассогласования 10% относительно Рэлеевского предела). Из рис. 3, а видно, что форма огибающей мало изменилась по сравнению с односигнальной ситуацией, изображенной на предыдущем рисунке.

Сигнал с выхода инверсного фильтра, изображенный на рис. 3, б имеет 2 отдельных пика, положение которых совпадает с истинными положениями фронтов импульсов, показанных рисками.

а	б
Рис. 3. Огибающая двух простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра

На рис. 4 показаны огибающие сигнала, образованного тремя перекрывающимися импульсами. Фронты импульсов отличаются по времени запаздывания на 100 дискретных отсчетов. Как и на рис. 3, а, форма огибающей не позволяет судить о числе импульсов, образовавших входной сигнал. Сигнал с выхода инверсного фильтра, изображенный на рис. 4, б имеет 3 отдельных пика, положение которых совпадает с истинным положением фронтов импульсов, что свидетельствует о разрешении отдельных импульсов.

а	б
Рис. 4. Огибающая трех простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра

Представленные результаты моделирования подтверждают справедливость изложенных выше теоретических выкладок, доказывают возможность повышения разрешающей способности по дальности методом инверсной фильтрации при отсутствии шума. Ниже представлены результаты моделирования устойчивости инверсной фильтрации к воздействию шума.

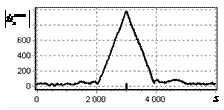
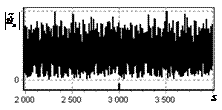
На рис. 5 показаны результаты, аналогичные рис. 2, при наложении на сигнал шума, распределенного по нормальному закону. Отношение сигнал-шум (ОСШ) в пике выходного сигнала оптимального фильтра (рис. 5, а) составляло 30 дБ.

Из рис. 5, б видно, что пик сигнала на выходе инверсного фильтра замаскирован шумами.

а	б
Рис. 5. Огибающая сигнала одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров при наличии шума. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра

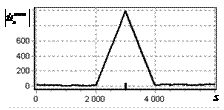
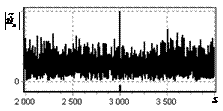
На рис. 6 показаны аналогичные результаты при ОСШ 36 дБ. Из рис. 6, б видно, что при таком ОСШ пик сигнала на выходе инверсного фильтра выше уровня шума.

а	б
Рис. 6. Огибающая сигнала одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров при наличии шума. ОСШ=36 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра

Из полученных результатов следует, что инверсная фильтрация требует достаточно высокого ОСШ. На практике существуют приложения, связанные с обнаружением и разрешением импульсных сигналов, в которых ОСШ 36 дБ и более достижимы. В таких приложениях инверсная фильтрация предложенным способом может использоваться без принятия дополнительных мер по выделению полезного сигнала на фоне шума. Однако для активного радара на практике характерны ситуации, при которых требуется разрешить сигналы при существенно меньшем ОСШ. Для разрешения методом инверсной фильтрации в условиях низкого ОСШ предлагается способ, заключающийся в ограничении снизу спектра опорного сигнала, представленного выражениями 2 – 6.

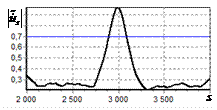
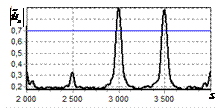
На рис. 7 представлены результаты, поясняющие суть ограничения снизу спектра опорного сигнала. На рис. 7, а показана огибающая спектра одиночного импульса, аналогичная рис. 1, а. Горизонтальной линией отмечен уровень ограничения. В обработке участвует та часть спектра, которая находится выше уровня, который в данном случае составляет 0,1 от максимума. На рис. 7, б показана огибающая спектра сигнала с выхода инверсного фильтра. Составляющие спектра, находящиеся ниже уровня ограничения равны нулю.

а	б
Рис. 7. АЧС простого радиоимпульса до и после инверсной фильтрации. Уровень ограничения снизу нормированного спектра опорного сигнала 0,1 а – АЧС простого радиоимпульса до инверсной фильтрации; б – АЧС простого радиоимпульса после инверсной фильтрации

Выражение для ОДПФ над ограниченным инверсным спектром в отличие от выражения имеет вид.

,

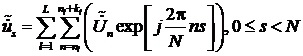где L – количество лепестков спектра, превышающих порог; l – номер текущего лепестка спектра, превысившего порог; n_l, – начальный номер спектральной составляющей l-го лепестка спектра, превысившей порог; k_l – количество спектральных составляющих l-го лепестка спектра, превысивших порог.

После необходимых преобразований получим

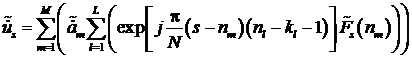
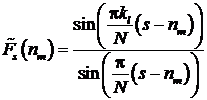
Величины максимальны при s=n_m. Но в отличие от выражения они не обращаются в нуль при других значениях s. Ширина главного лепестка зависит от числа спектральных составляющих k_l. Исходя из этого, огибающая сжатого сигнала каждой из М целей будет представлять собой сумму величин , умноженных на соответствующие амплитуды и иметь главный и боковые лепестки на оси дальности.

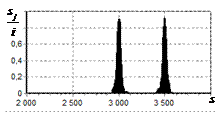
На рис. 8 представлены огибающие сигналов одиночного импульса с выхода инверсного фильтра, полученные для уровня ограничения 0,1 и 0,025 соответственно. Из рисунка видно, что с уменьшением уровня ограничения протяженность главного максимума огибающей выходного сигнала уменьшается, что способствует повышению разрешающей способности. Однако очевидно, что при этом будет возрастать уровень шума, поскольку на вход инверсного фильтра будут поступать спектральные составляющие дальних боковых лепестков, что видно из рис. 7, а.

а	б
Рис. 8. Огибающая сигнала одиночного простого радиоимпульса на выходе инверсного фильтра. ОСШ=36 дБ. Уровень ограничения снизу нормированного спектра опорного сигнала 0,1 а – уровень ограничения снизу нормированного спектра опорного сигнала 0,1; б – уровень ограничения снизу нормированного спектра опорного сигнала 0,025

Конкретный уровень порога ограничения выбирается из соотношения между требуемым разрешением и достижимым ОСШ.

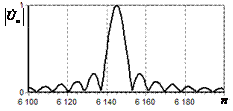
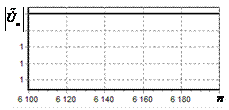
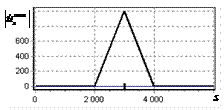
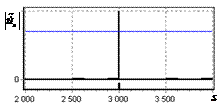
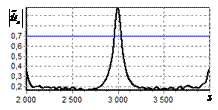
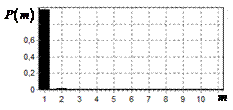
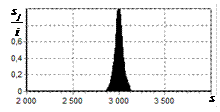
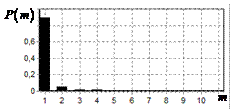
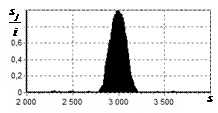
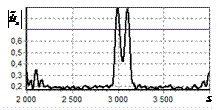
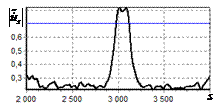
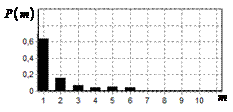
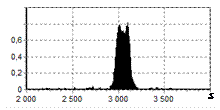
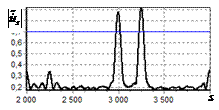
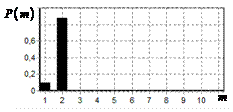
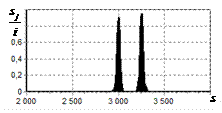
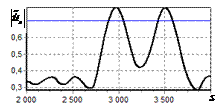
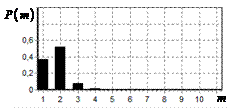
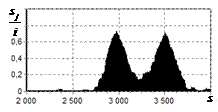
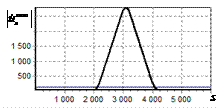
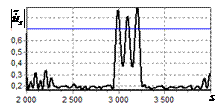
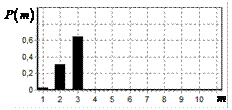
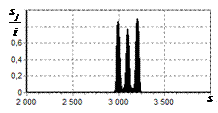
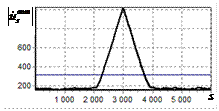
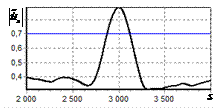
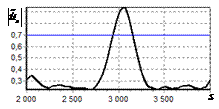
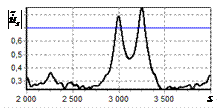
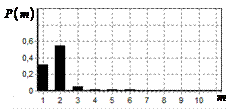
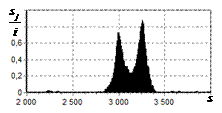
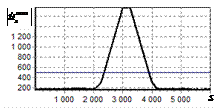
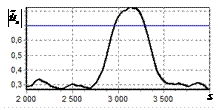
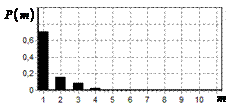
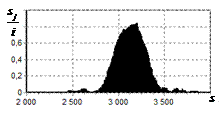
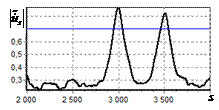
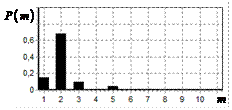
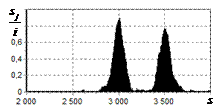
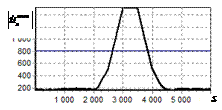
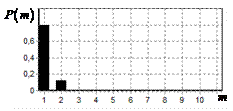
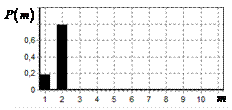
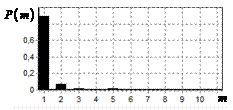
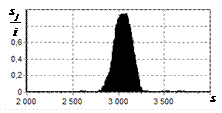
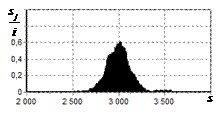
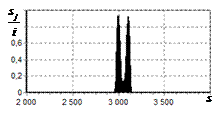
На рис. 9 – 11 представлены результаты моделирования способа инверсной фильтрации с ограничением снизу. На рис. 9 – 11, а и б показаны усредненные по 100 реализациям огибающие сигналов с выходов оптимального и инверсного фильтров соответственно, на рис. 9 – 11, в показаны вероятности определения числа импульсов, образующих входной сигнал, на рис. 9 – 11, г – гистограммы результатов измерения времени запаздывания сигнала инверсным фильтром. ОСШ составляло 30, 23 и 18 дБ для рис. 9, 10 и 11 соответственно.

а	б
в	г
Рис. 9. Огибающая сигнала одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 10. Огибающая сигнала одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=23 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 11. Огибающая сигнала одиночного простого радиоимпульса на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=18 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

Из представленных результатов видно, что во всех случаях число импульсов, образующих входной сигнал определяется правильно.

На рис. 12 – 14 представлены результаты работы оптимального и инверсного фильтров по сигналу, образованного двумя импульсами, сдвинутыми друг относительно друга на 0,1 от длительности импульса.

Из рисунков видно, что число импульсов, образовавших входной сигнал определяется правильно только при ОСШ 30 дБ. При более низких ОСШ решение преимущественно принимается в пользу одиночного сигнала.

а	б
в	г
Рис. 12. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 13. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=23 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 14. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=18 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

На рис. 15 – 17 представлены аналогичные результаты, полученные при взаимном сдвиге импульов 250 отсчетов (0,25 от длительности импульса). Из рисунков видно, что число импульсов определяется правильно при ОСШ, выше 23 дБ.

а	б
в	г
Рис. 15. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 250 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 16. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 250 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов, гистограмма оценок дальности. ОСШ=23 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 17. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 250 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=18 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

На рис. 18 – 20 показаны результаты, полученные при взаимном сдвиге между импульсами 0,5 от длительности импульса, что в 2 раза меньше Рэлеевского предела. Из рисунков видно, что в этом случае правильное решение принимается при всех исследовавшихся ОСШ. Огибающая сигнала с выхода оптимального фильтра во всех рассмотренных случаях не позволяет правильно оценить число импульсов, образовавших входной сигнал.

а	б
в	г
Рис. 18. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 500 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 19. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 500 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=23 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

а	б
в	г
Рис. 20. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 500 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=18 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

На рис. 21 представлены результаты, полученные в ситуации, когда входной сигнал был образован тремя импульсами, сдвинутыми друг относительно друга на 0,1 от длительности импульса. Из рисунка видно, что число импульсов определяется правильно.

а	б
в	г
Рис. 21. Огибающая сигнала двух простых радиоимпульсов, сдвинутых друг относительно друга на 100 дискретных отсчетов на выходе оптимального и инверсного фильтров, вероятность определения числа сигналов и гистограмма оценок дальности. ОСШ=30 дБ а – огибающая простого радиоимпульса на выходе оптимального фильтра; б – огибающая простого радиоимпульса на выходе инверсного фильтра; в – вероятность определения числа сигналов методом инверсной; г – гистограмма оценок дальности методом инверсной

В целом, приведенные результаты аналитических исследований и моделирования доказывают возможность разрешать сигналы отдельных импульсов способом инверсной фильтрации. Инверсная фильтрация простого (гладкого) радиоимпульса позволяет получить потенциальную разрешающую способность в один дискрет АЦП и определяется его интервалом дискретизации. Указанные характеристики разрешения достигаются при ОСШ от 36 дБ. При меньшем ОСШ отклик инверсного фильтра скрыт в шумах из-за чего вероятность правильного разрешения сигналов очень низка. Способ ограничения спектра опорного сигнала снизу позволяет уверенно разрешить сигналы инверсным фильтром при ОСШ от 18 дБ. В этом случае разрешающая способность определяется уровнем ограничения спектра и при ОСШ=18 дБ может достигать 0,5 от Рэлеевского предела. Анализ результатов моделирования позволяет сделать вывод, что реализация предложенного способа в активном радаре позволит без существенного снижения других технических характеристик повысить его разрешающую способность примерно в два раза.

ЛИТЕРАТУРА

1. Абраменков, В. В. Измерение координат радиолокационных целей методами многосигнальной радиолокации / В. В. Абраменков. – Смоленск : ВУ ВПВО ВС РФ, 2002. – 130 с.

2. Акимцев В. В. Разрешающая способность при цифровой обработке сигналов / В. В. Акимцев // Радиотехника. – 2004. – № 1. – С. 3 – 11.

3. Варюхин В. А. Основы теории многоканального анализа / В. А. Варюхин. – Киев : Наук. думка, 2015. – 168 с.

4. Василенко, Г. И. Теория восстановления сигналов: О редукции к идеальному прибору в физике и технике / Г. И. Василенко. – М. : Сов. радио, 1979. – 272 с.

5. Васильченко О. В. Интервал разрешения по дальности в РЛС с ЛЧМ-сигналом / О. В. Васильченко, С. М. Семченков // Труды Российского научно-технического общества радиотехники, электроники и связи им. А. С. Попова. Тринадцатая Международная конференция. Серия: Цифровая обработка сигналов и ее применение. DSPA–2011. Т. 1. – 2011. – С 153-156.

6. Корн Г. Справочник по математике для научных работников и инженеров, Г. Корн, Т. Корн. М. : Наука, 1973-849 с.

7. Марплмл С. Л. Цифровой спектральный анализ и его применение / С. Л. Марпл-мл ; пер. с англ. – М. : Мир, 1990. – 584 с.

8. Чижов А. А. Сверхрэлеевское разрешение. Т. 2: Преодоление фактора некорректности обратной задачи рассеяния и проекционная радиолокация / А. А. Чижов. – М. : КРАСАНД, 2010. – 104 с.

9. Гимаров В. А., Дли М. И., Круглов В. В. Задачи распознавания нестационарных образов //Известия Российской академии наук. Теория и системы управления. 2004. № 3. С. 92-96.

10. Дли М. И., Какатунова Т. В. Нечеткие когнитивные модели региональных инновационных систем // Интеграл. 2011. № 2. С. 16-18.

11. Бояринов Ю. Г., Борисов В. В., Мищенко В. И., Дли М. И. Метод построения нечеткой полумарковской модели функционирования сложной системы // Программные продукты и системы. 2010. № 3. С. 26.

12. Гимаров В. А., Дли М. И., Битюцкий С. Я. Нейро-нечеткий метод классификации объектов с разнотипными признаками //Системы управления и информационные технологии. 2004. Т. 16. № 4. С. 13-18.

13. Бояринов Ю. Г., Стоянова О. В., Дли М. И. Применение нейро-нечеткого метода группового учета аргументов для построения моделей социально-экономических систем // Программные продукты и системы. 2006. № 3. С. 7.

RESOLUTION ENHANCEMENT OF THE ACTIVE RADAR WITH SINGULAR BASE SIGNAL

BY THE INVERSE FILTERING METHOD

Semchenkov S. M., Savitsky F. L., Abramenkov A. V., Azersky M. A.

In the article is considered inverse filtering application characteristics to resolution enhancement of the active radar with singular base signal with the influence of normal distributed noise with 18 dB. Analitic description of the inverse filtering response to such signal in the time domain was received. It is indicated, that when the SNR is 36 dB and above, inverse filtering can adapting without additional processing techniques. In order to inverse filtering response was stand and allow to enable impulses when the SNR above 36 dB, is offer the spectrum mode of limitation of the relevant signal from below. The simulation data processing by method of one, two or three impulses when SNR is 18-30 dB was entered. The findings confirmed the possibility of the inverse filtering application to the resolution enhancement of the machining pattern impulse singular base signal with real attainable SNR.

Key words: singular base signal, resolution, superresolution, inverse filtering, concerted processing.

Смоленская областная общественная организация

общероссийской общественной организации

«Российское научно-техническое общество

радиотехники электроники и связи» им. А. С. Попова

(СООООООРНТОРЭС им. А. С.  Попова)

Поступила в редакцию 5.11.2015 г.
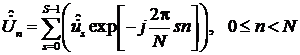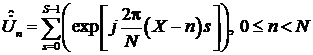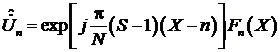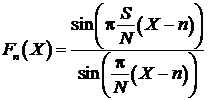
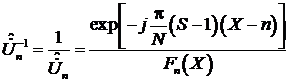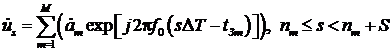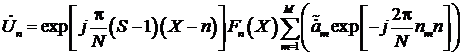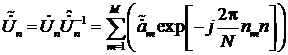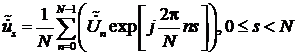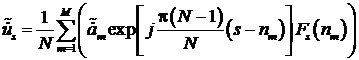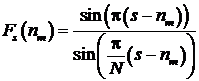