Мунерман В.И., Самойлова Т.А.

УДК 519.6:519.725:681.3

ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ ПРОГРАММИРОВАНИЕ

ДЛЯ СУПЕРКОМПЬЮТЕРОВ

Введение

Проблема программирования для суперкомпьютеров относится к числу сложнейших проблем. Эта сложность объясняется тем, что процесс распараллеливания алгоритмов трудно формализовать, и в большинстве случаев успех распараллеливания зависит от искусства программиста. Одно из решений указанной проблемы состоит в использовании параллелизма данных. Достоинство этого метода состоит в том, что программист отвлекается от идеи распараллеливания и отдает все силы созданию обычной последовательной программы, которая на самом деле выполняется параллельно, поскольку сами данные обрабатываются параллельно [1,2]. Не будет преувеличением сказать, что первые разработки параллелизма данных были сделаны в Институте Кибернетики им. В. М. Глушкова в работах В.А. Вышинского и З. Л. Рабиновича, в которых впервые в качестве базового типа данных для суперкомпьютеров были предложены матрицы. Полученные результаты были систематизированы в [3]. Настоящая статья посвящена методу программирования суперкомпьютеров на основе алгебры многомерных матриц [4], которая на наш взгляд наиболее удобна для алгоритмизации задач и структуризации данных [5, 6]. В настоящее время известен ряд исследований по применению многомерных матриц для представления данных в электронных таблицах и базах данных и знаний. Далее в тексте термины матрица и многомерная матрица обычно будут использоваться как синонимы.

Алгебра многомерных матриц

Рассмотрим кратко алгебру многомерных матриц. Обычно в математике рассматриваются числовые многомерные матрицы над полем действительных чисел. Однако в конкретных задачах матрицы могут содержать элементы произвольной природы. Кроме того, операции над элементами матриц не обязательно должны быть традиционными операциями сложения и умножения. Так в [7] рассматриваются матрицы над полукольцами (S, +, , 0, 1), где S - множество элементов, + и - соответственно ассоциативные аддитивная и мультипликативная операции, а 0 и 1 - нейтральные элементы для этих операций.

Пример 1. При решении задачи построения матриц доступности графа используется полукольцо ({0,1},,,0,1). В этом случае мы имеем дело с булевскими матрицами, элементы которых можно интерпретировать как "ложь" и "истина". В качестве аддититивной операции выступает дизъюнкция, а мультипликативной конъюнкция.

Пример 2. Для вычисления кратчайшего пути на графе используется полукольцо (R⁺,MIN,+,+,0). Здесь R⁺- множество неотрицательных действительных чисел. В качестве аддитивной операции выступает операция MIN с нейтральным элементом +, а в качестве мультипликативной - операция + с нейтральным элементом 0.

В общем случае для определения элементов матриц не требуются даже полукольца. Рассмотрим алгебраическую систему (S, +, ), где S - множество элементов, + и - соответственно аддитивная и мультипликативная операции. Такие системы будем называть 2-группоидами, так как от каждой операции требуется только замкнутость на множестве S. 2-груп-поид - наиболее общий тип для элементов матриц, так как предъявляет минимальные требования к операциям. . Выбор аддитивной и мультипликативной операций может быть достаточно традиционным, как в примере 1, и весьма экзотическим как в примере 2.

В дальнейшем мы будем считать, что элементы матриц принадлежат, по крайней мере, к 2-группоидам.

Определим p-мерную матрицу как совокупность элементов где индексы i₁,…,i_p принимают значения от 1 до n соответственно. Таким образом, p-мерная матрица содержит n_1…n_p элементов. Обозначим многомерную матрицу . Для многомерных матриц определяются операции сложения и умножения.

Суммой двух p-мерных матриц и с одинаковыми наборами индексов i₁,…,i_p называется p-мерная матрица с тем же набором индексов, элементы которой вычисляются по формуле .

Определим умножение многомерных матриц. Пусть даны две матрицы и , p и q-мерные соответственно. Разобьем совокупности индексов i₁,…,i_p и i₁,…,i_q на четыре группы, содержащие соответственно , , и индексов (, , , 0). Причем ++=p, а ++=q. Обозначим группы индексов как l=l₁,…,l, s=s₁,…,s, c=c₁,…,c и m=m₁,…,m. Представим матрицы A и B в виде и . Индексы групп s и c в матрицах A и B полностью совпадают. 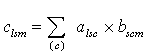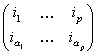Тогда матрица , элементы которой вычисляются по формуле , называется произведением матриц A и B. Произведение многомерных матриц называется (свернутым произведением и обозначается (AB). Из определения (свернутого произведения следует, что для любой пары многомерных матриц можно, подбирая различные значения и , построить много различных произведений. Традиционная для алгебры матриц операция транспонирования задается перестановкой индексов .

Для матриц, определенных над алгебраическими системами с обратимым элементом по умножению, определяется операция обращения матрицы.

Наконец для многомерных матриц определяется операция свертки матрицы. Свертка матрицы определяется через разбиение совокупности ее индексов i₁,…,i_p на группы s=s₁,…,s, c=c₁,…,c (+=p). Матрица (q=), называется сверткой матрицы А, если ее элементы вычисляются по формуле . Свертка матрицы A обозначается B=А.

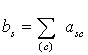
Многомерные матрицы и современные технологии

программирования

Обработка многомерных матриц хорошо согласуется с современными принципами и технологиями разработки программного обеспечения, в частности с объектно-ориентированным программированием, присущим всем современным языкам программирования, в том числе и языкам, используемым для программирования суперкомпьютеров.

Сама многомерная матрица легко представляется в виде объекта.

Совокупность данных этого объекта содержит:

число индексов матрицы и размерность каждого индекса;
массив, размерность которого совпадает с числом индексов;
вектор номеров индексов, определяющий перестановку для текущего транспонирования матрицы.

Базовыми методами этого объекта являются:

процедура инициализации;
функции, возвращающие значения элементов матрицы;
процедуры, изменяющие значения элементов матрицы;
процедура транспонирования;
процедура свертки.

От базового объекта могут быть порождены объекты сумма и (свернутое произведение матриц. Эти объекты наследуют все данные и методы базового объекта, но процедура инициализации порождает матрицу-сумму (произведение) матриц, заданных в ей в качестве параметров.

В качестве примера рассмотрим задачу построения матриц, элементы которых - кортежи, содержащие элементы разных типов. Такие матрицы целесообразно использовать при программирование программ обработки информации в базах данных и знаний.

Пример 3. Пусть дана совокупность типов данных, T₁,…,T_n, каждый из которых является по крайней мере 2-группоидом. Тогда кортеж c=(t₁,…,t_n), где t_iT_i (i=1,...,n), можно рассматривать как объект наследующий все свойства типов T₁,…,T_n, в том числе и операции сложения и умножения элементов кортежей. Для кортежей также можно определить аддитивную и мультипликативную операции. Это может быть поэлементное сложение и умножение. Такой подход позволяет нам определить многомерную матрицу кортежей как объект, наследующий свойства объекта-кортежа. Построение многомерной матрицы кортежей показано на рис. 1. Мы используем здесь принцип множественного наследования, присущий ряду современных языков программирования. Этот принцип использован только для наглядности, так как его отсутствие в конкретном языке не является препятствием для построения матриц кортежей. Направление наследования свойств на рисунке - сверху вниз.

Рис. 1. Объектная модель многомерной матрицы кортежей

Рассмотренные нами свойства многомерных матриц позволяют в заключение сформулировать один принцип, который позволяет облегчить алгоритмизацию задач, для решения которых необходимо использование суперкомпьютеров.

Принцип последовательно-параллельного программирования

Сформулируем принцип последовательно-параллельного программирования в виде следующих четырех положений:

- в качестве базового типа данных используется алгебра многомерных матриц;

- операции этой алгебры реализуются как базовые процедуры обработки данных для конкретных суперкомпьютеров, с максимально допустимой степенью параллелизма;

- многомерные матрицы включаются в языки программирования как самостоятельные объекты;

- алгоритмы представляются как последовательности операций над многомерными матрицами.

Перечислим основные достоинства принципа последовательно-параллельного программирования.

Во-первых, исключается связь между свойствами конкретной архитектуры суперкомпьютера и способностью данного алгоритма к распараллеливанию.

Во-вторых, ограничивается число реализуемых параллельно алгоритмов, так как необходимо распараллелить только операции алгебры многомерных матриц. Поэтому можно наиболее полно использовать возможности данного суперкомпьютера для оптимизации программ, реализующих эти операции.

В-третьих, алгоритм и программа, реализующие задачу из некоторой предметной области разрабатываются как обычные последовательные алгоритмы и программы. Данные, представленные в виде многомерных матриц, последовательно обрабатываются операциями алгебры многомерных матриц как неделимые объекты. Такой подход наиболее естественен для человека.

В-четвертых, программа выполняется на суперкомпьютере параллельно, так как каждая операция над многомерными матрицами реализуется параллельным алгоритмом.

Заключение

Параллельная обработка данных превращается сегодня из экзотики в естественный и необходимый при решении подавляющего большинства задач метод обработки данных. Это в свою очередь требует повышения эффективности работы программистов. Использование принципа последовательно-параллельного программирования позволяет использовать хорошо известные и отработанные и методы разработки, тестирования и отладки программ.

Представление информации посредством многомерных матриц, позволяет разрабатывать модели для различных предметных областей. Эти модели могут быть реализованы на суперкомпьютерах с минимальными затратами на программирование.

Например, анализ задачи оценки виброзащитных характеристик, при обработке результатов летных испытаний показал, что исходные данные удобно представляются с помощью многомерных матриц, а алгоритмы сводятся к выполнению операций над этими матрицами. Применение принципа последовательно-параллельного программирования при решении этой задачи позволяет существенно повысить эффективность этих алгоритмов благодаря параллельной реализации на суперкомпьютерах [6].

Одним из направлений использования метода последовательно-параллельного программирования являются экспертные системы. Многомерные матрицы представляют собой идеальное средство для классификации и представления правил принятия решений.

Сказанное позволяет надеяться, что применение изложенного в статье метода обеспечит возможность решения сложных задач, требующих больших объемов вычислений.

ЛИТЕРАТУРА

1. Fox G. C. Solving Problems on Concurrent Processors. - Prentice Hall, 1988.

2. Foster I. Designing and Building Parallel Programs. - Addison-Wesley Publishing Company, Inc, 1995.

3. Рабинович З. Л. Машинный интеллект и ЭВМ пятого поколения. - Киев. - Кибернетика. - №3. - 1985. - С. 95-107.

4. Соколов Н. П. Введение в теорию многомерных матриц. - Киев: Наукова думка, 1972.

5. Гендель Е. Г., Мунерман В. И. Применение алгебраических моделей для синтеза процессов обработки файлов. - УСиМ. - 1984. - № 4. - С.69-72.

6. Митенков В. Б., Конычев В. И., Емельченко Е. П., Муннерман В.И., Самойлов М. Ю., Самойлова Т. А. Эффективное решение задач обработки результатов летных испытаний на суперкомпьютерах. // Тезисы докладов к международной конференции "Авиационные технологии 2000". - Жуковский, 1997. - С. III-16.

7. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. - М., Мир, 1979.

Кафедра информатики

Смоленский государственный педагогический университет

Поступила в редакцию 3.07.99.