УДК 658.512.2:681.3.06
МЕТОД СОГЛАСОВАНИЯ СУБЪЕКТИВНЫХ ИЗМЕРЕНИЙ
В ИЕРАРХИЯХ МАТРИЦ
ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ
© 1999 г. Е.
В. Харитонов
В статье рассматривается новый метод
согласования субъективных измерений. Он
основан на декомпозиции исходной обратно
симметричной матрицы отношений предпочтения
сравниваемых объектов на матрицы меньшей
размерности при условии, когда значение
показателя отношения согласованности
субъективных оценок в матрице превышает
допустимый порог. В построенной иерархии матриц
производится анализ и согласование субъективных
оценок на каждом уровне иерархии начиная с
нижнего. Метод классифицируется как процедура
интеллектуального анализа данных и позволяет
повысить качество принимаемых решений в
системах поддержки принятия решений.
Задача выбора на множестве альтернатив решается методом анализа иерархий [1, 2]. Исходными данными задачи являются субъективные оценки, представленные в виде отношений предпочтения сравниваемых вариантов выбора (альтернатив). Например, если медицинский препарат А по мнению врача эффективнее препарата Б в два раза, то оценка отношения предпочтения препарата А к Б будет записана в виде Э(а,б)=2.
Субъективные оценки в виде отношений предпочтения сравниваемых альтернатив представляются в виде обратно симметричной матрицы доминирования. Такое представление позволяет устанавливать связь между оценками из разных строк и столбцов матрицы, определять собственный вектор матрицы, нормировать результат и получать вектор приоритетов для каждого из сравниваемых объектов.
Поскольку при практическом принятии решений субъективные оценки часто не согласованы и противоречивы, то актуальной научной задачей исследования является уменьшение ошибок в субъективных измерениях до уровня ошибок, допускаемых экспертами или до уровня погрешностей объективных измерений восстановлением отношения транзитивности между исходными данными.
В качестве меры оценки несогласованности исходных субъективных оценок выбран показатель "отношение согласованности" (OS) [1, 2]. Если OS=0, то все оценки согласованы, если OS с 0, то не согласованы. Чем больше значение OS, тем больше нарушено отношение транзитивности между оценками и они менее согласованы.
Восстановление транзитивности отношений между оценками является обязательным условием в получении непротиворечивых решений. Следовательно, задачей повышения качества принимаемых решений является восстановление транзитивности в отношениях предпочтения между исходными субъективными оценками.
Заявленная задача решается на основе предложенного автором "Способа определения локальной несогласованности субъективных оценок в обратно симметричных матрицах доминирования" и "Способа взаимной коррекции оценок" [3].
Способ определения локальной несогласованности состоит из процедур: структурной декомпозиции обратно симметричной матрицы доминирования на матрицы меньшей размерности и определения отношения согласованности для вновь полученных матриц. Построенная иерархия матриц представляет собой подграф полного графа матриц отношений предпочтения. Каждая вершина подграфа ассоциируется с матрицей и характеризуется значением отношения согласованности субъективных оценок, расположенных в этой матрице. Особенность представления матриц в виде графа древовидной структуры состоит в том, что разветвление вершин производится только при условии т OS с OSтр (где OSтр - требуемый уровень согласованности оценок). Вершины, характеризующиеся значением отношения согласованности, меньшим требуемого значения, отсекаются. Эта процедура позволяет существенно уменьшить количество матриц подлежащих анализу, сокращает время согласования исходных субъективных оценок.
Способ взаимной коррекции оценок состоит из процедур сравнения полученных матриц меньшей размерности на каждом уровне иерархии по показателю отношение согласованности, выделения двух матриц с максимальными значениями OS, определения одинаковых оценок в этих матрицах и получения новых значений оценок по взаимозависимым оценкам, расположенным в этих матрицах. Указанные процедуры применяются к оценкам в каждой из матриц подграфа на всех уровнях иерархии.
Пусть получены сравнительные оценки по пяти лекарственным препаратам в виде отношения предпочтений и записаны в матрицу М(5,5) =M5 (рис. 1). Значение OS матрицы М5 равно 14,8% и превышает требуемым порог согласованности OSтр (он выбран субъектом на уровне 12%). Требуется выделить область (или несколько областей) оценок, обладающих наибольшей ошибкой измерений, согласовать эти оценки, после коррекции исходных оценок получить коэффициенты важности для каждой из сравниваемых альтернатив и выбрать наиболее эффективное лекарство.
С целью отыскания наиболее искаженных субъективных оценок, к матрице М5 применяется способ структурной декомпозиции. Матрица М5 представляется в виде пяти матриц M41, M42, M43, M44, M45 вычеркиванием столбца и строки одинакового индекса. Особенностью такого представления субъективных оценок является то, что в матрицах меньшей размерности сохраняются все отношения предпочтения, присутствующие в исходной матрице доминирования.
Определяется значение отношения согласованности для вновь полученных матриц. Значения OS сравниваются с требуемым порогом согласованности OSтр. Поскольку значения OS для матриц М41 М42 и М43 не превышают OSтр, то принцип декомпозиции к этим матрицам не применяется. Значения OS для матриц М45 и М44 превышают OSтр, следовательно к этим матрицам применяется принцип декомпозиции и матрицы представляются в виде совокупности матриц меньшей размерности. На рис. 2 приведен пример представления матриц М44 и М45. Поскольку матрицы М441, М442, М443, М444, М451, М452, М453, М454 являются матрицами минимального размера, то их дальнейшая декомпозиция невозможна. Максимальным значением отношения согласованности обладают М444, М442, М454, М452. Согласование оценок производится способом коррекции исходных данных, основанном на методе согласования результатов субъективных измерений. Из сравнения матриц М444 и М442 следует, что общей локальной областью несогласованности для этих матриц является оценка "5" (см. рис. 2). Эта же субъективная оценка является общей для матриц М454 и М452, а следовательно, и для М45 и М44.
В приведенном примере согласуемой
оценкой является элемент, расположенный на
пересечении первой строки и третьего столбца
матрицы М5 (рис. 1). Скорректированное значение
этого элемента определяют из произведения
зависимых элементов 0.2![]() 2
= 0.4 матриц М444 или М454. После подстановки в первую
строку третьего столбца скорректированной
оценки 0.4 вместо 5, уменьшаются: OS452 с 25 до 8%; OS442 с
19.9 до 11.7%; OS44 с 28 до 8%; OS45 с 24 до 4%. Отношение
согласованности матрицы М5 уменьшилось с 14,8 до
7.5%. Изменились и коэффициенты эффективности
сравниваемых лекарств (табл. 1). Анализ таблицы 1
показал, что субъект (врач) завышал эффективность
использования лекарства "А" с одновременным
занижением эффективности использования всех
остальных лекарственных препаратов. Однако,
несущественная разница между исходным и
полученным значениями отношения
согласованности данных не привела к искажению
рангов лекарств и приоритетности в их
использовании. Большая точность результатов
может быть достигнута за счет снижения значения
OSтр.
2
= 0.4 матриц М444 или М454. После подстановки в первую
строку третьего столбца скорректированной
оценки 0.4 вместо 5, уменьшаются: OS452 с 25 до 8%; OS442 с
19.9 до 11.7%; OS44 с 28 до 8%; OS45 с 24 до 4%. Отношение
согласованности матрицы М5 уменьшилось с 14,8 до
7.5%. Изменились и коэффициенты эффективности
сравниваемых лекарств (табл. 1). Анализ таблицы 1
показал, что субъект (врач) завышал эффективность
использования лекарства "А" с одновременным
занижением эффективности использования всех
остальных лекарственных препаратов. Однако,
несущественная разница между исходным и
полученным значениями отношения
согласованности данных не привела к искажению
рангов лекарств и приоритетности в их
использовании. Большая точность результатов
может быть достигнута за счет снижения значения
OSтр.
Таблица 1
Коэффициенты эффективности применения лекарств и их ранги
Коэффициент эффективности (до коррекции) |
Ранг |
Коэффициент эффективности (после коррекции) |
Ранг |
|
| А | 0.17 |
3 |
0.11 |
3 |
| Б | 0.46 |
1 |
0.48 |
1 |
| В | 0.01 |
5 |
0.02 |
5 |
| Г | 0.31 |
2 |
0.33 |
2 |
| Д | 0.05 |
4 |
0.06 |
4 |
Так, при OSтр =0.09 дерево иерархии увеличивается за счет дополнительной декомпозиции матрицы М42 на матрицы меньшей размерности. Изменяется число анализируемых матриц на низшем уровне иерархии (это матрицы М442, М443, М444, М451, М452, М454), увеличивается число корректируемых элементов.
Вывод. Метод согласования субъективных
измерений в иерархиях матриц отношений
предпочтения позволяет корректировать исходные
субъективные данные и повышать качество
принимаемых решений. Исследования показали, что
метод позволяет корректировать субъективные
оценки из любой предметной области,
несогласованность которых не превышает 40%. К
несомненному преимуществу метода можно отнести
свойство адаптируемости принципа структурной
декомпозиции исходной матрицы доминирования в
зависимости от требований к уровню
согласованности оценок (то есть от значения OSтр).
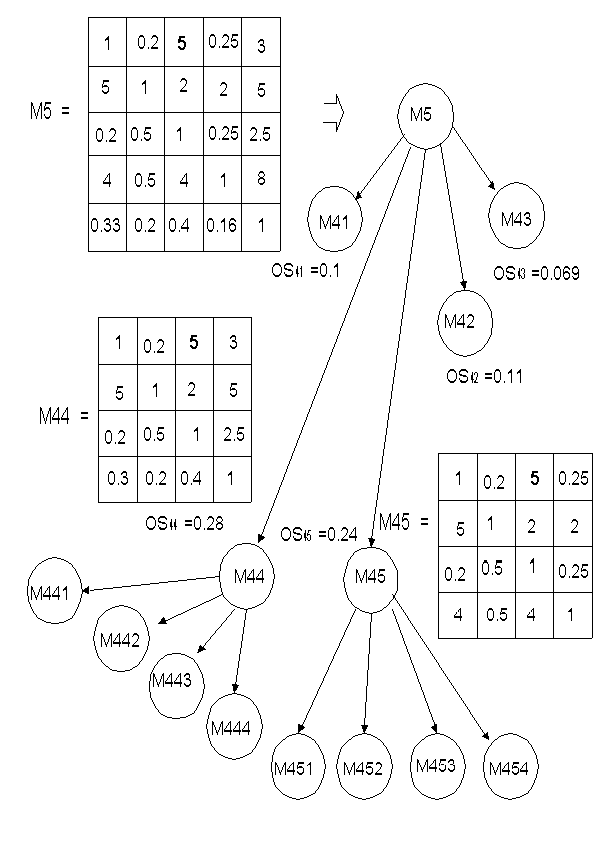
Рис. 1
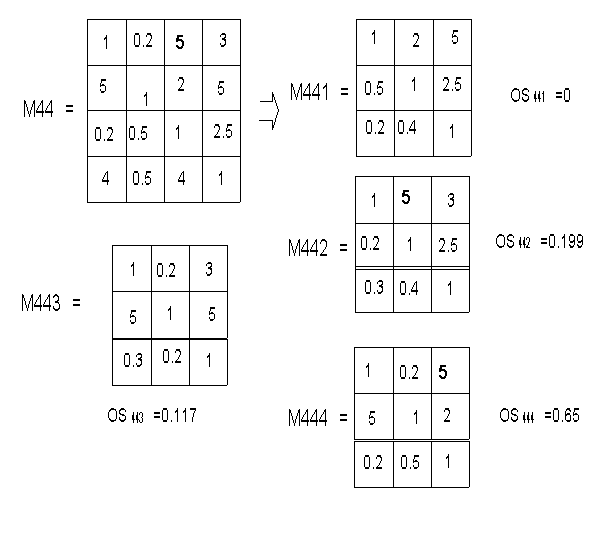
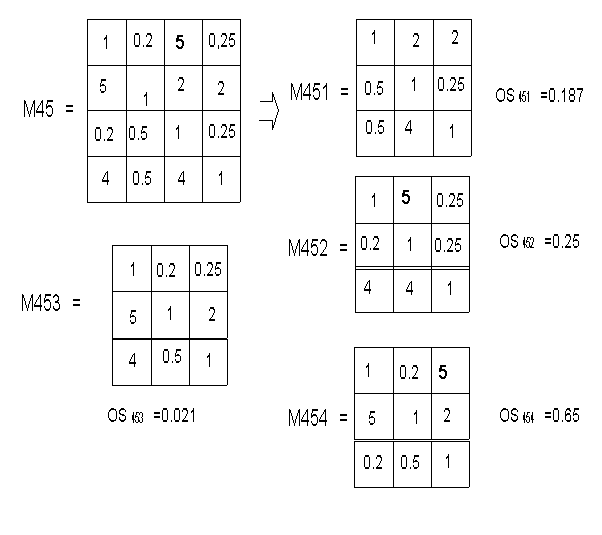
Рис. 2
ЛИТЕРАТУРА
1. Саати Т. Л. Принятие решений. Метод анализа иерархий. - М.: Радио и связь, 1993.
2. Саати Т. Л., Кернс К. Аналитическое планирование. Организация систем. - М.: Радио и связь, 1991.
3. Харитонов Е. В. Теоретическое обобщение и развитие методов принятия решений в условиях неопределенности функционирования организационно-технических систем управления ВПВО ВС РФ. - Смоленск: ВУ ВПВО СВ РФ, 1999. - 277 с.
Научно-исследовательский отдел
Военный университет ВПВО ВС РФ
Поступила в редакцию 8.09.99.