Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 16. -

Вып. 1. - 2017. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-53-html/TITL-53.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-53-html/cont.htm

 

УДК: 531.9+539.12.01

 

СТРУКТУРА АТОМНОГО ЯДРА И ПЕРИОДИЧЕСКИЙ ЗАКОН МЕНДЕЛЕЕВА

 

© 2017 г. Холманский А. С.

 

(holmansky.docx) (holmansky.pdf)

 

В работе смоделировали структуру ядра системой оболочек, состоящих из комбинаций сферических и кольцевых вихрей. Связав спин и магнитный моменты ядер с динамикой внешней оболочки ядра, определили ее тип и провели полуэмпирический расчет параметров ее структуры для стабильных и нестабильных изотопов ядер в последовательности порядкового номера Z от 1 до 37. Сопоставление полученных размеров ядер с радиусами электронных оболочек атомов позволило выявить определенную корреляцию. На основании ее заключили, что закономерности в изменении структуры атомного ядра могут детерминировать периодический закон Менделеева.

Ключевые слова: структура ядра; параметры внешних оболочек; корреляция радиусов ядер и атомов; периодический закон.

 

ВВЕДЕНИЕ

 

Д. И. Менделеев не только обосновал зависимость химических свойств элементов от их массового числа (А), но и предсказал, что «атомы простых тел суть сложные существа, образованные сложением некоторых еще меньших частей» и «периодическому закону будущее грозит не раз­рушением, а только надстройки и развитие быть обе­щаются» [1]. С открытием ядерно-электронной структуры атома число А в периодическом законе было заменено на заряд ядра или число протонов (электронов) в ядре (Z). Числом Z определяется порядковый номер атома в периодической системе Менделеева. В силу монотонности изменений А и Z их нельзя было напрямую связать с периодичностью свойств элементов. Решить эту проблему удалось только с применением формализма квантовой механики и экспериментальных данных атомной спектроскопии. Правила квантования энергии и заселенности электронных уровней, а также представления об электронных орбиталях и оболочках позволили связать химические свойства веществ с физическими свойствами   электронных структур атомов и молекул. При этом периодичность свойств элементов была объяснена повторением схемы построения их внешней электронной оболочки через определенные периоды в последовательности чисел Z (Рис 1).

Стабильность пространственно-энергетической иерархии электронных оболочек атома обусловлена взаимодействием между ядром и электронами. Причем, учитывая порядок отношения масс электрона и протона (~10–3),  можно условно считать, что электроны маркируют своими орбиталями силовые линии собственного электромагнитного поля атома. Влияние заряда ядра, его спина и магнитного момента на форму и энергетику этого поля особенно отчетливо проявляется на элементах с малыми значениями числа Z. Например, спин протона в атоме водорода во многом определяет физико-химические свойства воды [2,3]. Влияние ядра на электронные уровни атомов проявляется на их оптических свойствах, что позволяют определять спин ядра, его магнитный и квадрупольный моменты и зарядовый радиус () [4,5].

При всей очевидности участия ядер в формировании электронных конфигураций атомов зависимость их физико-химических свойств от структуры ядер в атомной физике не принимается во внимание. Руководствуясь законами диалектики и используя правила квантовой механики, автор разработал алгоритм построения и расчета вихревой модели структур элементарных частиц и ядер [6-8]. Достоверные опытные данные в алгоритме играют роль граничных условий. Таким образом, рассчитали вихревые структуры нейтрона, протона и электрона в основном и возбужденном состояниях.  

 

 

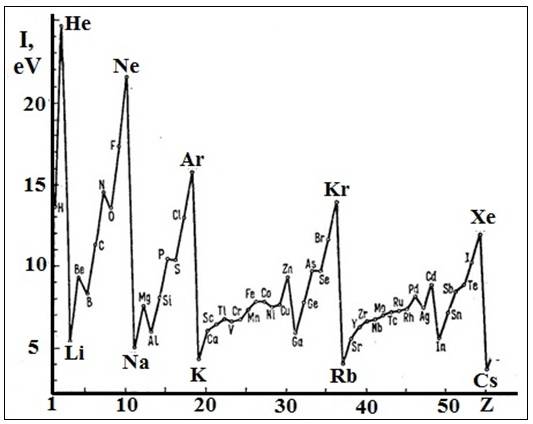
Рис 1. Зависимости потенциалов ионизации атомов от порядкового номера (Z).

 

В настоящей работе алгоритм применили для расчета вихревых структур стабильных и нестабильных изотопов элементов с Z от 1 до 37 с целью выявления корреляций между параметрами структуры ядра и физико-химическими свойствами элементов. Ряд элементов с Z от 1 до 37 включает практически все макро и микроэлементы, свойства которых обусловили возникновение, а затем и развитие земной биосферы. Кроме того этот ряд элементов достаточен для иллюстрации периодического закона Менделеева (Рис 1). 

 

МАТЕРИАЛЫ И МЕТОДЫ

 

Для расчетов брали данные по массе (m), заряду (q), спину (S), магнитному (μ) и квадрупольному моменту (Q) ядер из [9]. При выборе оптимальной структуры ядра учитывали знак Q. В образовании магнитно-массового скелета ядерной структуры участвуют в общем случае три тороидальных вихря – сфероподобнная оболочка (Sh) и два кольцеобразных вихря, расположенных внутри (In) и вне (Ex) оболочки (Рис 2). С этими вихрями динамически связаны потоки электромагнитной энергии, образующие овал Кельвина и отвечающие за электрические характеристики ядра [7,8]. На Рис 2а овал Кельвина обозначен пунктирной линией.  

Толщина слоя оболочки и собственный радиус колец считали много меньшими их радиусов (r) и полагали rin= rsh. Правила сборки Sh, In и Ex из начальных хиральных вихрей (энергоформ, далее – ЭФ) описаны в [6-8]. Структура ядра включала систему вложенных закрытых оболочек (CSH), образованных из коррелированных пар протонов pp*, далее – (рр) и нейтронов nn*, далее – (nn) с инверсными спинами. Момент импульса () элементов нуклонов в таких парах равнялся нулю, а электрический заряд () суммировался. Для CSH полагали . CSH имели нулевые S и μ, а их r определялся только квантовым числом (k), которое зависело от Z, но не зависело от числа пар.

 

 

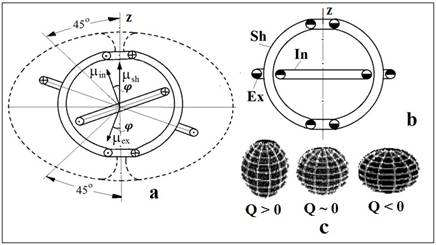
Рис. 2. Принципиальные схемы устройства открытой (а) и закрытой (b) оболочки ядра. Плюсы, точки и закрашенные наполовину кружки обозначают направления вращений элементов магнитного скелета ядра. Пунктиром условно обозначена область потоков электромагнитной энергии отвечающих за природу электрического заряда ядра и знак квадрупольного момента (с).

 

Внешние открытые оболочки (ОSH) ядер (Рис 2а) имели различное число неспаренных нейтронов (n) и протонов (p). Рассчитывали следующие типы ОSH: n-подобная ОSH, содержащая n, 3n, 5n; р-подобная ОSH – содержащая p или 3p; d-подобная, гибридная ОSH состава: np; 2n+p, 2p+n, 3p+n. Тип ОSH выбирали с учетом величины S и знака Q, варьируя при этом углы проекций векторов  на ось вращения ядра (ось z на Рис 2). Положительный знак Q, то есть растяжение структуры ядра по оси z, связывали с отклонениями  на углы . Растяжение в направлении перпендикулярном z (отрицательный знак Q) связывали с отклонением  на углы , (Рис 2). Соответственно, величина cosφ, равная отношению проекции  на ось z к   при этом была меньше или больше значения .    При установлении типа внешней оболочки учитывали значения энергий отделения первых n или p от ядер, определив их по дефектам масс (см. Таблицу 1). Качественная согласованность между типом оболочки и значениями энергий  служила дополнительным критерием в выборе модели структуры ядра.

 

Таблица 1

Типы и энергия отделения нуклонов от внешних оболочек

 

 

Z

 

Ядро

Энергия

отделения (эВ)

Тип внешней

оболочки

Продолжение таблицы

1

2

3

4

5

n

Р

19

K39

13,1

6,8

3p

1

2

3

4

5

19

K40*

7,8

7,6

np

2

He4

20,6

19,8

CSH

20

Ca40

15,7

8,3

CSH

3

Li7

7,3

10

p

20

Ca41*

8,4

8,9

3n

4

Be9

8,1

16,9

3n

21

Sc45

11,4

6,9

2n+p

5

B10

8,5

6,6

3p+n

21

Sc46*

8,9

8,3

np

5

В11

11,4

11,2

2n+p

22

Ti48

11,7

11,5

CSH

5

B12*

3,4

14,2

np

22

Ti49

8,2

11,6

n

6

C11*

13,1

8,8

n

23

V50*

9,3

7,9

3p+n

6

C12

18,7

16

CSH

23

V51

11,1

8,1

p

6

C13

5

17,6

2p+n

24

Cr52

12,1

10,5

CSH

6

C14*

8,2

20,8

CSH

24

Cr53

7,9

11,1

n

7

N13*

20,1

1,9

2n+p

25

Mn52*

10,6

6,6

3p+n

7

N14

7,1

0,5

np

25

Mn55

10,6

8,1

3p

7

N15

17,9

10,2

2n+p

26

Fe56

11,2

10,2

CSH

8

O15

13,2

14,3

n

26

Fe57

7,7

10,6

n

8

O16

15,6

15,6

CSH

27

Co59

10,5

7,3

3p

8

O17

4,2

13,9

3n

28

Ni58

12,2

8,2

CSH

9

F17*

16,8

0,6

3p

28

Ni61

7,8

9,9

n

9

F19

10,4

8,0

p

29

Cu63

10,7

6,3

2n+p

10

Ne20

16,9

12,8

CSH

30

Zn64

11,9

7,7

CSH

10

Ne21

6,8

12,8

n

30

Zn65*

8,0

7,7

3n

11

Na23

12,4

8,8

3p

31

Ga68*

8,3

6,5

np

12

Mg24

16,5

11,8

CSH

31

Ga69

10,3

9

p

12

Mg25

8,8

12,1

n

32

Ge70

11,6

8,6

CSH

13

Al27

21,3

8,3

3p

32

Ge71*

7,4

8,3

n

13

Al28*

7,7

9,5

np

32

Ge73*

6,7

10

5n

14

Si28

17,2

11,6

CSH

33

As75

10,2

6,9

3p

14

Si29

8,5

12,4

n

34

Se77

6,4

9,6

n

15

P31

12,3

7,3

p

34

Se80

9,9

11,3

CSH

16

S32

11,2

18,2

CSH

35

Br81

10,2

7,1

3p

16

S33

8,7

9,6

3n

35

Br82*

7,6

8,4

3p+n

17

Cl35

12,7

6,4

2n+p

36

Kr83

7,5

9,8

3n

17

Cl36*

8,6

8,0

3n+p

36

Kr84

10,5

10,7

CSH

18

Ar36

15,6

8,3

CSH

37

Rb85

10,5

7,1

3p

18

Ar40

9,9

12,5

CSH

37

Rb86

8,6

8,5

np

 

Параметры структуры CSH и OSH рассчитывали, решая системы уравнений (1)-(5)  с учетом условий (6)-(9). Эмпирическое значение магнитного момента ядра( – ядерный магнетон Бора) приравнивали сумме проекций Sh, In и Ех внешней ОSH. Для OSH, содержащей j нуклонов масса m = , где .

, (1); ,  (2);

, (3); (1)-(3) –  квантование вращательных моментов.

, (4) – выражение для магнитного момента ядра.

, (5) – равенство энергии вращения и энергии покоя ядра. 

, (6) – условие цельности вихревой структуры ядра.

 

,  (7); m =  (8); ,  (9).

 

Индекс i в суммах и в (6) соответствует Sh, In, Ex; е – единичный заряд. Условие (9) для р: для n: . Отметим, что в структуре ядра In и Ex орбитали р меняются местами.  Уравнения (1)-(3), (5)-(7) для CSH ядрасоставили, представив CSH состоящей из двух коррелированных пар (рр) и (nn) c k=2. Решение системы для гелиоподобной CSH, с любым числом четверок [(nn)(pp)] дает рекуррентную формулу для радиуса CSH.

 

.               (10)

 

При конденсации двух четверок [(nn)(pp)] образуется неустойчивая структура дважды «магического» изотопа Ве8*, которая распадается за с на две α-частицы. Учитывая это, формулу (10) применяли кроме Не4 только для Ne20 и Ar36, а для других ядер внешние CSH представляли состоящими из обособленных CSH (nn)-типа и (рр)-типа. При этом число пар в этих оболочках могло различаться.  Рекуррентные формулы для радиусов и отношений масс элементов этих CSH имели вид:

 

,        (11)

,                                                        (12)

,       (13)

 ,                            (14)

 

Известно [10], что у изотопов Са и переходных металлов  различался не более чем на 1-2%, а  изотопов Zn был больше  изотопов Са на ~12%. Учитывая эти данные, при подборе k в формулах (11)-(14) принимали во внимание результаты расчетов изотопов с OSH и фиксировали значения k в рядах родственных элементов. Например, для ядер с внешней CSH (рр)-типа в формуле (13) принимали  для ряда Mg24 – Ar40 и   для ряда  Ca40 – Se80. При этом число  в формуле (11) увеличивалось по мере роста числа (nn)-пар в CSH и, начиная с Ge70 брали . В этих случаях оболочка (nn)-типа становилась внешней.

Для примера покажем схему расчета OSH (2n+p)-типа для ядра Cl35 (S=1,5ћ, ; Q = –1,8 ). Для k=6 имеем  Для получения S=1,5ћ и отрицательного знака Q вектор надо повернуть на угол φ, при котором cosφ = (13,5/16,5=0,818>0,76). При этих условиях уравнения (1)-(5) имеют вид:

 

;;;

;

.

 

Решая этих уравнения с учетом условий (6)-(9) при , получили параметры CSH для Cl35 (см. Таблицу 2). При расчетах параметров табличные величины округляли до второго знака после запятой и с такой же точностью вычисляли параметры ядра.

 

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

 

Результаты расчетов 129 стабильных и нестабильных изотопов элементов с Z от 1 до 37 приведены в Таблице 2. При этом общее число вариантов расчетов структур превышало 260, то есть в среднем каждый расчет дублировался и отбирался вариант, наилучшим образом удовлетворяющий опытным данным.

Зависимость величин  или  (в случае ) от Z хорошо согласуется с эмпирической зависимостью  для  [5] (Рис 3). Расчетные радиусы сопоставляли с известными размерами ядер, полученные в опытах по рассеянию на ядрах различных частиц и с помощью лазерной спектроскопии атомов. Эти методы позволяют рассчитывать . Например, первый метод для ядер Не3, He4, Ве9, C12 дает : 1,97; 1,68; 2,52; 2,37 Фм  [10,11]. Для нестабильных изотопов He6*, He8*; Ве7*, Ве10*, Ве11* второй метод дает : 2,07; 1,93; 2,65; 2,35; 2,45 Фм [12,13], соответственно. Поскольку  характеризует овал Кельвина [14] (Рис 2), то  и  могут быть меньше  особенно для OSH.

 

 

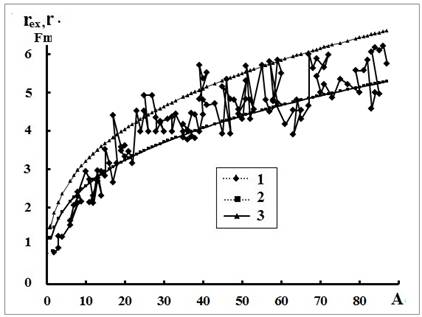
Рис. 3. Зависимость от массового числа А радиусов вихревой структуры ядра (1) и эмпирическая зависимость  c =1,2 (2) и 1,5 (3).

 

Таблица 2

 

Структура и параметры внешних оболочек ядер

 

 

Z

 

Ядро

 

Структура

()

 

  cosφ

 

%

Фм

0

n

Sh-Ex

120

72

28

0,24

0,85

1

1

p

In-Sh-Ex

45

32

26

0,58

0,93

1

1

d

(pn)

64

43

28

Ex0,5/1

0,41

0,85

1

1

t

(nn)p

81

53

23

0,33

0,96

1

2

He3

(pp)n

75

41

23

0,8

1,27

2

2

He4

(nn)(pp)

21

43

38

1,25

1,25

2

2

He6*

2(nn)(pp)

17

56

44

1,57

1,51

3-2

2

He8*

3(nn)(pp)

13

57

43

2,14

1,51

4-2

3

Li6

(pp)3n+p

25

50

40

Ex 7/8

1,52

1,68

2

3

Li7

2(nn)(pp)p

20

41

23

1,32

2,09

2

3

Li 8*

2(nn)(pp)np

15

50

30

1,76

2,32

3

4

Be9

(nn)2(pp)3n

12

60

40

Ex9/12

2,17

2,1

4

5

B8*

(nn)2(pp)np

16

51

29

1,74

2,42

3

5

B10

2(nn)(pp)3p+n

14

48

24

In 5/9

1,85

2,97

3

5

B11

2(nn)2(pp)2n+p

13

43

39

In 3/4

1,89

2,75

4

5

B12*

3(nn)2(pp)np

14

48

33

In 2/3

1,86

2,13

3

5

B13*

3(nn)2(pp)2n+p

12

42

39

In 3/4

1,9

2,72

4

6

C11*

2(nn)3(pp)n

13

57

43

Ex 2/4

2,13

2,15

4

6

C12

3(nn)3(pp)

11

38

31

1,57

2,34

3

6

C13

3(nn)2(pp)2p+n

14

46

30

In 2/6

2,36

2,98

3

6

С14*

4(nn)3(pp)

11

38

31

2,14

2,34

4-3

7

N13*

2(nn)3(pp)2n+p

13

44

38

In 2/4

1,85

2,8

4

7

N14

3(nn)3(pp)np

11

49

32

In 2/4

2,5

2,96

4

7

N15

3(nn)3(pp)2n+p

13

44

37

In 2/4

1,82

2,86

4

8

O15

3(nn)4(pp)n

11

45

55

Ex 4/5

3,55

2,15

5

8

O16

4(nn)4(pp)

8,3

40

30

2,14

3,18

4

8

O17

 3(nn)4(pp)3n

10

58

42

Ex11/15

2,62

2,68

5

8

O18

 5(nn)4(pp)

8,3

40

30

 

2,72

3,18

5-4

9

F17*

4(nn)3(pp)3p

9,5

45

21

In 4/12

2,79

4,43

4

9

F19

5(nn)4(pp)p

8,8

42

32

In 1/4

3

3,61

4

9

F20*

5(nn)4(pp)np

8,4

50

32

In 3/5

3,21

3,64

5

10

Ne19*

4(nn)5(pp)n

7,5

61

39

Ex4/5

3,05

3,51

5

10

Ne20

5(nn)5(pp)

7,9

47

35

3,37

3,37

5

10

Ne21

5(nn)5(pp)n

8,7

60

40

Ex4/6

3,14

3,48

6

10

Ne22

6(nn)5(pp)

8,3

40

30

9,2

2,72

3,18

5-4

11

Na23

6(nn)4(pp)3p

9,6

45

21

In 3/15

2,77

4,54

4

12

Mg24

6(nn)6(pp)

6,6

40

30

2,72

4,01

5

12

Mg25

6(nn)6(pp)n

8,1

65

35

Ex4/7

3,41

4,55

7

12

Mg26

7(nn)6(pp)

6,6

40

30

 

3,29

4,01

6-5

13

Al25*

6(nn)5(pp)3p

7,8

45

21

In 4/12

3,09

4,95

4

13

Al27

7(nn)5(pp)3p

7,8

45

21

In 4/12

3,09

4,95

4

13

Al28*

7(nn)6(pp)np

6,9

50

32

In 4/6

3,9

4,38

6

14

Si28

7(nn)7(pp)

6,6

40

30

2,72

4,01

5

14

Si29

7(nn)7(pp)n

6,4

54

46

Ex6/7

4,23

3,53

7

14

Si30

8(nn)7(pp)

6,6

40

30

 

3,87

4,01

7-5

15

P29*

7(nn)7(pp)p

9,4

44

22

In 1/4

2,82

4,28

4

15

P31

8(nn)7(pp)p

9,4

44

22

In 1/4

2,81

4,33

5

15

P32*

8(nn)7(pp)np

6,9

50

32

In 2/6

3,9

4,39

6

16

S32

8(nn)8(pp)

6,6

40

30

3,87

4,01

7-5

16

S33

7(nn)8(pp)3n

6,8

51

49

Ex18/21

4,46

3,35

7

16

S35*

8(nn)8(pp)3n

6,8

56

44

Ex4/7

4,01

3,71

7

17

Cl35

8(nn)8(pp)2n+p

7,1

51

36

Sh13,5/16,5

3,8

3,85

6

17

Cl36*

8(nn)8(pp)3n+p

7,1

51

40

Sh20/24

3,8

3,55

6

17

Cl37

9(nn)8(pp)2n+p

7,1

52

36

Sh13,5/16,5

3,79

3,87

6

17

Cl38

9(nn)8(pp)3n+p

7

51

40

Sh20/24

3,84

3,51

6

18

Ar35

7(nn)9(pp)3n

6,4

54

46

Ex18/21

4,19

3,55

7

18

Ar36

9(nn)9(pp)

6,6

48

35

4,08

4,08

6

18

Ar37

8(nn)9(pp)3n

6,8

51

49

Ex18/21

4,48

3,34

7

18

Ar38

10(nn)9(pp)

5,8

58

41

0,06

4,45

4,01

8-5

18

Ar39

9(nn)9(pp)3n

6,8

57

43

Ex16/21

4

3,72

7

18

Ar40

11(nn)9(pp)

5,8

58

41

4,45

4,01

8-5

19

K39

10(nn)8(pp)3p

7,6

46

21

In3/15

3,5

5,74

5

19

K40*

10(nn)9(pp)np

7,6

54

26

In5/6

3,56

5,39

6

19

K41

11(nn)8(pp)3p

7,4

50

20

In3/15

3,78

5,55

5

20

Ca39*

9(nn)10(pp)n

5,7

53

47

Ex5/7

4,86

3,86

8

20

Ca40

10(nn)10(pp)

5,4

40

30

4,45

4,84

8-6

20

Ca41*

9(nn)10(pp)3n

5,8

56

44

Ex19/24

4,69

4,19

8

20

Ca43

10(nn)10(pp)3n

5,7

55

45

Ex19/24

4,74

3,38

8

21

Sc45

11(nn)10(pp)2n+p

6,7

50

38

In 5/6

3,95

3,74

6

21

Sc46*

12(nn)10(pp)np

6

51

31

In 5/7

4,45

5,38

7

21

Sc47*

12(nn)10(pp)2n+p

6,8

50

38

In 5/6

3,94

3,68

6

22

Ti45*

11(nn)11(pp)n

7

65

35

Ex4/8

3,95

5,19

8

22

Ti47

12(nn)11(pp)n

6,6

62

38

Ex5/8

4,13

4,86

8

22

Ti48

13(nn)11(pp)

5,4

40

30

4,45

4,84

8-6

22

Ti49

13(nn)11(pp)n

8,2

65

35

Ex4/7

3,39

4,58

7

23

V50*

13(nn)10(pp)3p+n

7

42

34

In 8/15

4,34

4,1

5

23

V51

14(nn)11(pp)p

7,4

45

22

In 4/5

3,58

5,34

5

24

Cr49*

12(nn)12(pp)n

6,2

59

41

Ex5/8

4,42

4,47

8

24

Cr51*

13(nn)12(pp)n

6,7

62

38

Ex4/8

4,13

4,86

8

24

Cr52

14(nn)12(pp)

5,4

40

30

4,45

4,84

8-6

24

Cr53

14(nn)12(pp)n

5,9

57

43

Ex6/8

4,58

4,28

8

25

Mn51*

13(nn)11(pp)3p

7,6

45

21

In 4/15

3,51

5,72

5

25

Mn52*

13(nn)11(pp)3p+n

7

43

33

In 8/15

4,34

4,14

5

25

Mn55

15(nn)11(pp)3p

7,6

45

21

In 4/15

3,5

5,74

5

26

Fe56

15(nn)13(pp)

5,4

40

30

4,45

4,84

8-6

26

Fe57

15(nn)13(pp)n

5,9

50

50

Ex6/7

4,52

3,3

7

26

Fe59*

16(nn)13(pp)n

5,7

55

45

Ex6/8

4,76

4,14

8

27

Co57*

15(nn)12(pp)3p

7,6

46

20

In 5/15

3,49

5,83

5

27

Co58*

15(nn)13(pp)np

5,6

48

35

In 3/7

4,8

4,7

7

27

Co59

16(nn)12(pp)3p

7,6

46

20

In 5/15

3,48

5,88

5

27

Co60*

16(nn)12(pp)3p+n

8,2

48

25

In 7/15

3,79

5,53

5

28

Ni58

15(nn)14(pp)

5,4

40

30

 

4,45

4,84

8-6

28

Ni61

16(nn)14(pp)n

8,8

61

39

Ex4/6

3,73

4,19

6

29

Cu63

16(nn)14(pp)2n+p

5,9

50

38

Sh15,5/19,5

4,56

4,38

7

29

Cu65

17(nn)14(pp)2n+p

5,9

50

38

Sh15,5/19,5

4,56

4,38

7

30

Zn63*

16(nn)15(pp)n

6,9

57

43

Ex5/7

3,93

3,81

7

30

Zn64

17(nn)15(pp)

5,4

40

30

4,45

4,84

8-6

30

Zn65*

16(nn)15(pp)3n

6,2

53

47

Ex17/21

4,33

3,45

7

30

Zn67

18(nn)15(pp)n

7,1

59

41

Ex4/7

4,57

4,68

7

31

Ga67*

18(nn)15(pp)p

7,7

46

20

In 2/5

3,46

6,03

5

31

Ga68*

18(nn)15(pp)np

5

49

33

In 2/8

5,31

5,67

8

31

Ga69

19(nn)15(pp)p

7,6

46

20

In 2/5

3,47

5,92

5

31

Ga71

20(nn)15(pp)p

7,5

45,5

21

In 2/5

3,52

5,68

5

31

Ga72*

20(nn)15(pp)np

4,8

50

32

In 4/8

5,44

6,01

8

32

Ge69*

18(nn)16(pp)n

4,9

48

52

Ex5/8

5,45

3,66

8

32

Ge70

19(nn)16(pp)

5,4

58

42

5,02

4,84

9-6

32

Ge71*

19(nn)16(pp)n

5,1

50

50

Ex5/8

5,24

3,78

8

32

Ge73*

18(nn)16(pp)5n

5,5

54

46

Ex33/40

4,89

4

8

33

As75

21(nn)15(pp)3p

7,4

45

22

In 3/15

3,57

5,38

5

34

Se77

21(nn)17(pp)n

5,1

50

50

Ex7/8

5,24

3,77

8

34

Se80

23(nn)17(pp)

5,4

58

42

 

5,02

4,84

9-6

35

Br79

22(nn)16(pp)3p

7,5

45

21

In 3/15

3,52

5,6

5

35

Br81

23(nn)16(pp)3p

7,5

45

21

In 3/15

3,52

5,6

5

35

Br82*

23(nn)16(pp)3p+n

8,1

49

24

In 7/15

3,76

5,87

5

36

Kr83

22(nn)18(pp)3n

5,6

55

45

Lex18/24

4,61

4,23

8

36

Kr84

24(nn)18(pp)

4,6

41

29

5,02

4,84

9-6

36

Kr85*

23(nn)18(pp)3n

5,9

56

44

Lex18/24

4,98

4,25

8

37

Rb83*

23(nn)17(pp)3p

7,7

46

20

In 4/15

3,45

6,09

5

37

Rb84*

23(nn)18(pp)np

5,2

50

32

In 3/8

5,13

6,21

8

37

Rb85

24(nn)17(pp)3p

6,3

46

20

In 4/15

3,44

6,13

5

37

Rb86

24(nn)18(pp)np

5,3

51

30

In 3/8

5,07

6,23

8

37

Rb87

25(nn)17(pp)3p

5,9

43

25

In 3/18

4,49

5,77

6

Примечание: *) – обозначение нестабильных изотопов; 1) значения относятся  к радиусам  и , соответственно.

 

Следует отметить, что оценки  зависят от теоретической модели распределения заряда в ядре и механизма взаимодействия зондирующих частиц с ядром [5]. Как правило, используют модель, в которой плотность заряда спадает от единицы до нуля по экспоненте в поверхностном слое ядра с толщиной t~2,3 Фм (рис. 4). Данный слой можно соотнести с потоками ЭФ, образующими овал Кельвина. Распределение заряда в OSH с наружной Ех оказалось подобно распределению заряда в n [8,15] (рис. 4).

Овал Кельвина формируется в основном потоками ЭФ, генерируемые внешними OSH и СSH. Эти потоки в сумме с потоками ЭФ внутренних СSH  связывают вихревую структуру ядра в единое целое, то есть играют роль ядерных сил. Вне овала Кельвина на расстояниях более  действие его потоков на ЭФ внешней среды проявляется силовыми линиями электрического поля ядра. Можно предположить, что конфигурации этого поля будут чувствительны к типам внешних OSH и СSH и это скажется на энергии и форме электронных орбиталей атома.

 

 

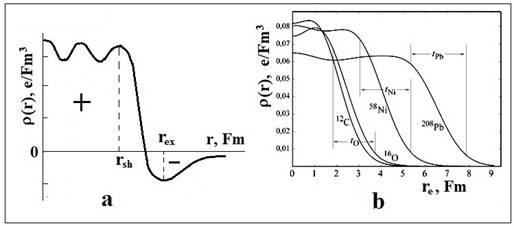
Рис. 4. Распределение плотности заряда в ядрах: (а) – вихревая модель, (b) – рассеяние электронов [11]. Толщина поверхностного слоя  t ~ 2.4 Фм.

 

 

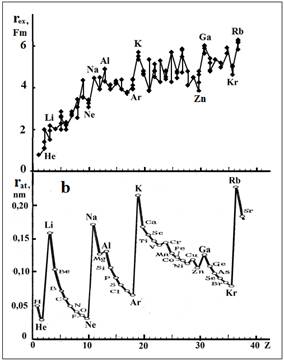
Рис. 5. Зависимости радиусов ядер (a) и орбитальных радиусов атомов (b) от порядкового номера (Z).

 

Предложенная в работе структура внешних OSH и СSH коррелирует с энергией отделения n и р от ядра, о чем свидетельствуют данные табл. 1. Кроме того расчеты размеров и  знака квадрупольного момента внешней оболочки позволяют моделировать динамику и форму овала Кельвина.

Очевидно, что эти характеристики ядра  влияют на геометрию его электрического поля, а значит, и на конфигурации электронных оболочек атома, от которых зависят их химические свойства. Действительно, сравнение размеров ядер и атомов  показало наличие корреляции для элементов в начале и конце периодов в последовательности Z (Рис 5).

Таким образом, можно заключить, что вихревая структура ядра вносит определенный вклад в формирование электронных оболочек атомов и закономерности в изменении типов внешних оболочек и размеров ядер в последовательностях порядкового номера проявляются на периодическом законе Менделеева.

 

ВЫВОДЫ

 

1. В рамках законов классической квантовой механики и вихревого движения построена модель структуры ядра, состоящая из вложенных друг в друга оболочек, образованных из сферических и кольцевых вихрей.

2. Показано, что структурой и типом внешней оболочки ядра в основном определяются: энергия отрыва первого нуклона от ядра, его спин, магнитный момент, форма и размеры.

3. Правила формирования внешней оболочки ядра с учетом эмпирических характеристик ядер как граничных условий позволили рассчитать частоту  спина оболочки, распределение массы и радиус.

4.  Корреляция между зависимостями радиусов ядра и атома от порядкового числа Z свидетельствует о детерминированности периодического закона Менделеева закономерностью в формировании вихревой структуры ядра.

 

ЛИТЕРАТУРА

 

1. Ельяшевич М. А., Периодический закон Д. И. Менделеева, спектры и строение атома, УФН –1970. – Т. 100. – Вып. 13. –С. 6–43.

2. Kholmanskiy A., Activation energy of water structural transitions // Journal of Molecular Structure. (2015) 1089. – Р. 124–128.

3. Захаров С. Д., Орто/пара спин-изомерия молекул Н2О как ведущий фактор формирования в воде двух структурных мотивов. [Электронный ресурс]. Режим доступа: http://www.biophys.ru/archive/h2o-00025.pdf.

4. Гангрский Ю. П., Марков Б. Н., Ядра в лучах лазера. М.: Знание, 1984. –64 с.

5. Сивухин Д. В., Общий курс физики. Том 5. Атомная и ядерная физика. – М.: Физматлит, 2002. – 784 с.

6.  Холманский А. С. Фрактально-резонансный принцип действия // МИС-РТ-2003г. Сборник № 29-2. URL: http://www.ikar.udm.ru/sb/sb29-2.htm

7. Холманский А. С. Хиральность  и  квантовые  эффекты как факторы  морфогенеза // Математическая морфология. Электронный математический и медико-биологический журнал.  - Т. 9. - Вып. 4. - 2010. - URL: http://www.smolensk.ru/user/sgma/MMORPH/N-28-html/kholmanskiy-2/kholmanskiy-2.htm.

8. Холманский, А. С. Вихревые модели электрона и нуклонов // Там же. – 2011. - Т.10. – Вып.2. - URL: http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/kholmanskiy-3/kholmanskiy-3.doc.

9. Физические величины: Справочник. – М.: Энергоатомиздат, 1991. – 1232 с.

10. Варламов В. В., Гончарова Н. Г., Ишханов Б. С., Физика ядра и банки ядерных данных: учебное пособие.-М.: Университетская книга, 2010. -246 с.

11. Хофштадтер Р., Структура ядер и нуклонов // УФН. –1963. –Т.81. –С. 185–200.

12. Wang L.-B., Müller P., Laser Spectroscopic Determination of the 6He Nuclear Charge Radius // Phys. Rev. Lett. 93, 2004. 142501.

13. Müller P. et al. Nuclear Charge Radius of 8He // Phys. Rev. Lett. 2007. 99, 252501.

14. Махaньков В.  Г., Рыбаков Ю. П., Санюк В. И., Модель Скирма и сильные взаимодействия (К 30-летию создания модели Скирма) // УФН. 1992, №2. С.1-61

15. Недорезов В. Г., Мушкаренков  А. Н., Электромагнитные взаимодействия ядер // [Электронный ресурс]. Режим доступа:  http://nuclphys.sinp.msu.ru/eint/index.html.

 

THE STRUCTURE OF THE ATOMIC NUCLEUS AND THE PERIODIC LAW OF MENDELEEV

 

Holmansky A. S.

 

In the modeled structure of the core shells system, consisting of a combination of spherical and ring vortices. Coupled spins and magnetic moments of the nuclei with the dynamic of the outer shell of the nucleus, to determine the type and calculated parameters of structure of stable and unstable isotopes of nuclei in the sequence of the serial numbers Z from 1 to 37. A comparison of the size of the nuclei with the radii of the electron shells of atoms revealed certain correlation. On its basis we concluded that the patterns change in the structure of the nucleus appear on Mendeleev's periodic law.

Key words: nuclei structure; the parameters of the outer shells; the correlation radii of nuclei and atoms; periodic law.

 

Научно-испытательная лаборатория ООО «ФЛЛ»

Москва

allexhol@ya.ru

Поступила в редакцию 26.02.2017.