Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 16. -
Вып. 1. - 2017. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-53-html/TITL-53.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-53-html/cont.htm
На правах рукописи
КУЗНЕЦОВ Геннадий Васильевич
ОБРАБОТКА ИНФОРМАЦИИ ДЛЯ АНАЛИЗА
СОСТОЯНИЯ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ МЕТОДАМИ
ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
Специальность 05.13.01 – Системный анализ, управление
и обработка информации
(биологические
науки)
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора биологических наук
Тула – 2009
Работа выполнена на кафедре медико-биологических дисциплин ГОУ ВПО
«Тульский государственный университет»
Научный консультант: заслуженный деятель науки РФ,
доктор
биологических наук, доктор технических наук,
профессор Яшин Алексей Афанасьевич
Официальные оппоненты:
Доктор биологических наук,
доктор физико-математических наук,
профессор
Еськов Валерий Матвеевич
Доктор биологических наук Жеребцова Валентина
Александровна
Доктор биологических наук,
профессор Панфилов Олег Петрович
Ведущая организация: ГОУ ВПО
«Смоленская государственная медицинская академия»
Защита состоится __________
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Тульский государственный
университет» по адресу:
Автореферат разослан «___»__________2009 г.
Ученый секретарь диссертационного
совета,
доктор медицинских
наук
Борисова О.Н.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы.
Моделированию кровеносной системы человека посвящено большое количество работ
отечественных и зарубежных ученых. Первыми работами, положившими начало таких
исследований, можно считать работы Гарвея и Ньютона. Всплеск
таких исследований начался во второй половине 20 века, когда к исследованиям по
моделированию сердечно-сосудистой системы (ССС) человека стали привлекать
математический аппарат и вычислительную технику (F.S. Grodins (1966), P.L. Vadot (1968), L. Pater (1966) и
др.).
Уместно упомянуть фамилии авторов,
которые занимались моделированием ССС и результаты которых описаны в первой
главе данной диссертации: Хадарцев А.А. (1997), Милованов А.В. (1997), Субботина Т.И. (2003), Яшин А.А.
(2003), Дж. Педли (1986), Федоров С.Ю. (1997), Гайтон Н.А. (1969), Pincus S.M. (1993), Eleisher L.A. (1993), Phillips W.M. (1993) и др.
В основе конкретной модели ССС лежат
принципы, присущие только этой модели, чем и были обусловлены трудности в
описании и решении конкретных проблем. При решении задач, которые появляются
как в теоретических исследованиях, так и при решении вопросов клинического
плана, приходится пользоваться несколькими моделями, каждая из которых
создается, в основном, для решения конкретной проблемы. Поэтому встает
необходимость создания определенной модели (или нескольких) в рамках другой
(или нескольких) моделей и наоборот. Необходимо объединяющее начало. Подходы, предлагаемые к настоящему времени (E.H. Starling, A. Hill, Хаютин В.М., Шумаков В.И., Бакусов
Л.М., Лищук В.А, и др.) обуславливали анализ большого
числа параметров, от которых зависит поведение ССС, а при более детальном
описании ее функционирования появляется тенденция к еще большему увеличению
числа параметров.
Нахождение объединяющего начала в задачах,
касающихся моделирования ССС, является в настоящее время актуальным. Наряду с
переносом вещества по кровеносной системе, происходит и перенос информации.
Установлено, что понятие информации тесным образом связано с жизнедеятельностью
человека (Кадомцев Б.Б., Яшин А.А.). Объяснение закономерностей, на основании
которых передается информация внутри организма и ее обработка, является
актуальным для исследования.
Единство компонентов ССС можно объяснить
изучением ее геометрии в структуре определенного пространства. Моделирование
движения крови, как во всей системе, так и в ее отдельных участках,
основывается на геометрии интегральных линий вектора скорости крови.
Анализируя современные исследования в
области моделирования ССС, можно сделать вывод, о значимости тематики
предпринятого исследования, позволяющего решить те задачи, для которых ранее не
было предложено логически выверенного концептуального обоснования, не была
разработана теория моделирования кровотока, которая с единых позиций позволяла
решать задачи обработки информации и
анализа состояния ССС человека. Применение дифференциальной геометрии
для теоретического и практического исследования движения крови ранее так широко не использовалось.
Таким образом, разработка моделей,
алгоритмических процедур и методов для анализа состояния ССС на базе
разработанного математического аппарата является актуальной
научно-теоретической и научно-практической проблемой.
Цель
и задачи исследования. Целью
диссертации является создание теории обработки информации для анализа
состояния сердечно-сосудистой системы на основе дифференциальных форм.
В соответствии с поставленной целью необходимо решить следующие задачи:
1. Разработать специальный математический
аппарат для моделирования системы кровообращения, основанный на использовании
дифференциальных форм.
2. Предложить способ формализации
деятельности ССС человека для более быстрой обработки информации ее состояния.
3. Синтезировать критерий оптимизации
пространства описаний системообразующих факторов, как для всей системы
кровообращения, так и ее отдельных участков.
4. Предложить структуру принятия решений
при формализованном описании ССС человека в задачах анализа, обработки
информации и управления при диагностике состояния исследуемой системы.
5. Предложить алгоритм управления
процессами контроля и диагностики состояния ССС.
6. Провести апробацию результатов,
полученных с использованием предложенных методов и моделей в экспериментальных
исследованиях с использованием ультразвуковых анализаторов.
7. Синтезировать процедуру оценки эффективности обработки информации состояния ССС
методами дифференциальных форм.
Предметом исследования
является информация о состоянии ССС для ее анализа, полученная на основе
структурных характеристик траекторий движения частиц крови.
Объектом исследования являются траектории движения частиц
крови.
Научная
новизна результатов исследования.
Впервые разработана теория для обработки
информации состояния сердечно-сосудистой системы человека с использованием
дифференциальных форм, отличающаяся предложенной математической моделью ССС, и
обеспечивающая получение адекватной информации для определения и достижения
отдельных ее целей.
Определены процедура и методы анализа
структурных характеристик системы кровообращения, основанные на принципах
целостности и делимости системы, что обеспечивает выделение ее структурных
свойств, рационализацию анализа, классификацию и выделение неадекватных видов
движения крови для управления патологией.
Предложена методология описания
турбулентного и ламинарного движений крови, характеризующие траектории движения
частиц крови в норме и при патологических изменениях в сосуде и во всей системе
кровообращения, позволяющая повысить информационную поддержку принятия
управленческих решений, как в отдельном сосуде, так и во всей системе.
Разработана структура информационного
обеспечения формализованного описания ССС человека, отличающаяся интеграцией
предложенных в работе методов, моделей и систем уравнений в единую
концептуальную систему анализа режимов работы ССС.
Предложен метод управления процессами
диагностики состояния ССС человека, отличающийся возможностью гибко менять
тактику ее проведения в зависимости от точки исследования с помощью
ультразвуковых анализаторов и разработанного математического обеспечения,
обеспечивающий выделение негативных факторов в траекториях движения крови.
Созданы математическая и графическая модели
системы кровообращения, отличающиеяся представлением системы кровообращения
посредством геодезических линий специального вида риманова пространства –
субпроективного, что обеспечивает исследование системы кровообращения с
допустимой статистической погрешностью и автоматизацию ее диагностики.
Разработаны процедура и таблицы
прогнозирования патологических изменений системы кровообращения, отличающиеся
учетом данных на основе известных методов и методов, полученных на основе
предложенного математического аппарата, обеспечивающего более точное
прогнозирование патологии.
Выявлены системные связи в системе
кровообращения на основе алгоритма управления контроля и диагностики ее
состояния, отличающиеся формализацией описания на основе графической зависимости
кровотока от времени, обеспечивающие принятие необходимых решений для
диагностики и устранения патологических изменений.
Предложен метод принятия решений по
коррекции обнаруженных патологических изменений, отличающийся использованием
структурной схемы поддержки принятия решений врачом.
Разработана математическая модель
управления комплексной оценкой эффективности обнаружения патологических
изменений, включающая таблицы показателей качества, их анализ, обеспечивающая
полноценность анализа результативности.
Научно-практическое
значение диссертации.
Создана теория для обработки информации о
состоянии всей ССС, ее отдельных участков с единых методологических позиций,
которая обеспечивает повышение эффективности и индивидуализацию лечения при
заболеваниях ССС.
Предложены подходы изучения видов движений
крови в рамках всей ССС и по отдельным участкам, на основании геометрических
характеристик траекторий движения крови.
Создан алгоритм управления процессами
контроля и диагностики состояния ССС.
Предложено исследование внутрисердечной
гемодинамики на основе геометрических характеристик шумов сердца.
Структурная схема системы позволяет
обеспечить поддержку принятия решений сосудистыми хирургами.
Полученные результаты легли в основу исследований по обработке информации о
состоянии ССС конкретных людей с привлечением ультразвуковых анализаторов,
рационализирована диагностика обнаружения патологических изменений на более
ранних стадиях их появления.
Предложенный подход обработки информации
позволяет научно обосновать методики применения свойств
траекторий движения частиц крови в обработке информации состояния ССС.
Разработанный математический аппарат
успешно используется при классификации видов движения крови в ССС для
обнаружения патологических изменений на ранних стадиях.
Внедрение
результатов работы.
Результаты исследования внедрены в
исследованиях ГУП НИИ НМТ; в исследованиях Института гастроэнтерологии АМН
Украины; Курском государственном медицинском университете; Курганском
государственном университете; Новгородском государственном университете им. Я.
Мудрого; Курском государственном техническом университете; Ростовском
государственном медицинском университете; Московском государственном университете
им. М.В. Ломоносова; Арзамасском государственном
педагогическом институте им. А.П. Гайдара; Пермском государственном техническом
университете.
Апробация работы. Основные результаты
работы были представлены в период с
Публикации. Самостоятельно и в соавторстве по теме
диссертации опубликовано 52 научная работа, в том числе 24 – в изданиях,
рекомендованных ВАК РФ. В работах, опубликованных в соавторстве и приведенных в
конце автореферата, лично автором представлены идеи и методы, используемые при
моделировании ССС и ее участков, а также были проведены необходимые вычисления
и эксперименты. Все основные результаты этих работ получены автором данной
работы. В монографиях [1, 2] результаты получены автором данной работы. В
работах [4 – 6, 8 – 10, 12 – 13, 18, 20, 22, 29 – 34, 36, 39, 47 – 48, 51],
выполненных в соавторстве, основные результаты и уравнения получены непосредственно
автором работы и обсуждались с соавторами
Структура и объем работы.
Диссертационная работа состоит из введения, восьми глав, заключения, списка
литературы и приложений; изложена на 366 страницах, содержит 36 рисунков, 10
таблиц. Список литературы включает 224 названия.
Основные положения, выносимые на защиту.
1. Теория и концепция представления ССС
человека как пространства материальных сред живого для получения необходимой
информации о состоянии ССС на основе математического аппарата дифференциальной
геометрии.
3. Обработка информации о состоянии ССС
человека с привлечением внешних дифференциальных форм имеет преимущества перед
теориями, базирующихся на дискретных методах.
4. Методология для описания турбулентного
движения крови методами геометрии субпроективных пространств позволяют
диагностировать нарушения гемодинамики на ранней стадии.
5. Модель ламинарного движения крови с
использованием геометрических характеристик траекторий
движения частиц крови эффективна при исследовании движения крови в
норме.
6. Моделирование движения частиц крови на
основе геометрии евклидова пространства по участку ССС, обеспечивает получение о
нем необходимой информации и проведение анализа состояния кровотока.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во
введении обосновывается
актуальность диссертации, сформулированы цели и задачи исследования, научная
новизна и практическая значимость исследования, приведены сведения об
апробации, внедрении работы и краткое содержание глав диссертации.
В первой главе, являющейся
расширенным введением в проблематику работы, содержится как анализ результатов,
полученных ранее отдельными исследователями и научными школами, включая работы
по данному направлению автора данного исследования и автора с коллегами.
Решаются задачи по формализации деятельности ССС человека и оптимизации
пространства описаний системообразующих факторов для всей системы
кровообращения и ее отдельных участков. Проанализированы существующие концепции
подходов к моделированию ССС.
Систематизированы и охарактеризованы биофизические и математические
аспекты пространственного подхода к моделированию ССС, включающего в себя
рассмотрение геометрии ССС как геометрию пространства определенного вида
(субпроективного пространства) для описания структуры ССС и геометрии евклидова
пространства для изучения геометрии отдельного участка сосудистой системы.
Вполне логичным для вводной главы является
исследование и выявление на логико-понятийном уровне сущности пространственного
подхода к обработке информации состояния ССС, а также структуры пространства,
сопоставляемого пространству кровеносной системы, свойства которого позволяют
проанализировать геометрию ССС и ее состояние.
В сосуде поток крови имеет непрерывный
характер, поэтому возникающие при создании теории конгруэнции и поверхности
можно исследовать обычными в дифференциальной геометрии методами. В результате
такого подхода получаем геометрическую картину и необходимые характеристики
стационарного потока крови, что до сего времени изучалось мало (рис. 1).
Рис. 1. Схематическое представление геометрической картины.
Вторая глава посвящена созданию
необходимого математического аппарата для обработки информации и анализа движения крови
по участку сосуда.
Так как при рассмотрении геометрии участка
сосуда используется геометрия евклидова пространства,
то переход от одной точки к другой можно осуществлять, основываясь как на
свойствах дифференцируемых отображений между областями евклидова пространства,
так и на свойствах дифференцируемых отображений между различными евклидовыми
пространствами. Более подробно рассматриваются конформные и геодезические
отображения, так они позволяют проследить движение крови вдоль сосуда и в
кровеносной системе.
Дается понятие подповерхности уровня
коэффициента конформности – так называемой эквиконформной гиперповерхности, то
есть гиперповерхности, на которой коэффициент конформности принимает постоянное
значение. Показывается, что такие поверхности являются гиперсферами в n-мерном
евклидовом пространстве.
Конформные отображения позволяют
обрабатывать информацию о видах движения крови, при которых сохраняются углы
между векторами скорости крови в точке сосуда и в ее образе. Сходящееся векторное
поле можно представить следующим образом (рис. 2):
Рис. 2. Пример сходящегося векторного поля.
Движение частиц крови происходит по
«кратчайшим» линиям, которым в пространстве, являющимся моделью пространства
ССС, будут соответствовать геодезические линии. Как и в случае конформного
отображения, рассматривается вектор геодезического преобразования.
Доказывается, что эквигеодезические гиперповерхности являются гиперплоскостями
(Рис 3).
Геометрия дифференцируемых отображений
тесным образом связана с геометрией гиперраспределений.
Приведенные результаты позволяют
характеризовать геометрическую картину движения крови в кровеносном сосуде с
использованием хорошо изученной геометрии различного вида гиперраспределений и
различного вида дифференцируемых отображений как между однородными, так и не
однородными пространствами.
В третьей главе, являющейся
центральной для создания теории обработки информации состояния ССС методами
дифференциальных форм, решаются задачи по разработке специального математического аппарата, и
предлагается структура при формализованном описании ССС для анализа и получения
информации о состоянии системы кровообращения.
Рис. 3. Гиперплоскости, ортогональные вектору скорости крови.
Вычисление компонент тензора
деформации приводит к тому, что компоненты этого тензора имеют вид:
(1)
который
аналогичен виду соответствующего тензора для конформного соответствия между
евклидовыми пространствами. В последнем равенстве величины a A и a A = g AB a B являются
компонентами вектора конформного преобразования. Здесь же находятся компоненты
ковариантного тензора кривизны субпроективного пространства:
(2)
где
и 
, а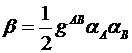 
.
Полученные величины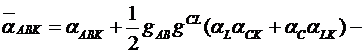 
- a B a AK - a A a BK удовлетворяют свойству:
,
что
с выражением для R ABKL
являются необходимыми и достаточными условиями для того, чтобы риманово
пространство было конформно-евклидовым. На основании приведенных рассуждений
делается вывод: конформное отображение между евклидовым и римановым
пространствами определяет в евклидовом пространстве конциркулярное векторное
поле, которое является одним из видов торсообразующего векторного поля.
По аналогии с конформным отображением
между евклидовыми пространствами, вводится понятие эквиконформных
гиперповерхностей, которые также являются гиперсферами. На основании введенного
понятия делается вывод, что
конформное
отображение между евклидовым и римановым пространствами определяет в евклидовом
пространстве гиперсферы, на которых коэффициент конформности принимает постоянные
значения.
Изучается не только гиперсфера в
евклидовом пространстве, но и ее образ. При этом произведение радиусов
эквиконформных гиперсфер, одна из которых является образом другой, постоянно.
Более того, на эквиконформной гиперсфере конциркулярное векторное поле,
определяемое конформным отображением между евклидовым и римановым
пространствами, является сходящимся векторным полем (рис. 4).
u Vn En
Рис. 4.Пример поверхностей, которым ортогонален вектор
скорости крови, при анализе движения
крови по всей системе кровообращения.
В завершении рассмотрения конформных
отображений, рассматриваются конформные соответствия между евклидовым
и субпроективным пространствами. Из конформно-евклидовых
выделяются субпроективные пространства. Это возможно тогда и только тогда,
когда тензор 
имеет вид:
. (3)
На эквиконформных гиперсферах вектор
конформного преобразования является сходящимся векторным полем.
Так как конформное отображение определяет
в евклидовом пространстве конциркулярное векторное поле, то оно будет
переходить в конциркулярное векторное поле тогда и только тогда, когда
пространство допускает такое векторное поле, то есть оно должно быть субпроективным.
Отсюда получен еще один результат: при конформном отображении
между евклидовым и римановым пространствами, конциркулярное векторное поле
будет переходить в конциркулярное векторное поле тогда и только тогда, когда
риманово пространство является субпроективным.
Ввиду того, что
траектории частиц крови представляют собой геодезические линии, рассматривается
и геодезическое соответствие между евклидовым и римановым пространствами.
Находятся компоненты тензора связности для данного отображения и компоненты
тензора кривизны. Вводится понятие эквигеодезической гиперповерхности, которая
определяется в евклидовом пространстве при его геодезическом отображении в
риманово пространство. При этом доказывается факт о эквигеодезических
гиперповерхностях в виде: эквигеодезические гиперповерхности являются
гиперплоскостями в евклидовом пространстве En.
При выяснении геометрии
вектора геодезического преобразования, делается вывод: геодезическое
отображение между евклидовым и римановым пространствами порождает в евклидовом
пространстве конциркулярное векторное поле, которое на эквигеодезических
гиперплоскостях является параллельным векторным полем.
Даются характеристики векторам второго
порядка, которые присутствуют в уравнениях перемещения репера 
риманова пространства
в некоторой карте U. Приводятся формулы для вычисления
векторов в случае произвольного дифференцируемого отображения между евклидовым
и римановым пространствами, а также для случаев, когда отображение является конформным
и геодезическим.
Полученные в этой главе результаты
позволяют использовать специальный математический аппарат для анализа движения
крови по всей ССС.
Четвертая глава посвящена разработке
теории для обработки информации при стационарном движении крови в участке
сосуда. Решаются задачи по разработке теории кровотока, методов исследования
ламинарного и турбулентного движений крови. Показано, что оптимальным
пространством описаний системообразующих факторов является евклидово
пространство, как частный случай субпроективного. Получены уравнения движения
крови по участку сосуда. В начале главы рассматриваются некоторые основные
идеи, подчеркивающие возможность и продуктивность применения геометрии в
исследовании ССС.
Для функции j вычисляется градиент, который по взаимным векторам 
для выбранной основной
тройки векторов 
, имеет вид:
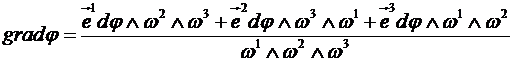. (4)
В этом же параграфе вычисляются дивергенция и
ротор вектора скорости крови. С учетом обозначений:
w 32 = - w 23 = pA w A = p, w 13 = - w 31 = qA w A = q,
w 21 = - w 12 = r A w A = r
уравнение
неразрывности потока крови имеет вид:
(dv 1
– v 2 r + v 3 q) Ù w 2 Ù w 3 + (d
v 2 – v 3 p + v 1 r) Ù w 3Ù w 1 +
+ (d v 3 – v 1 q + v 2 p) Ù w 1 Ù w 2 = 0.
Вычисляются
и компоненты вихря, который находится следующим образом:
.
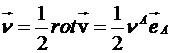Вводится понятие полной энергии частицы (H), которая
определяется из равенства:
.
Правая часть последнего равенства
обращается в нуль для перемещений, направления которых совпадают либо с
направлением скорости, либо с направлением вихря, либо же с любым направлением,
компланарным первым двум. Все эти перемещения лежат на поверхностях семейства
так называемой «постоянной энергии».
Далее рассматриваются поверхности
постоянной энергии и постоянной полной энергии (скорость постоянна), которые
характеризуются тем, что на них функция H принимает постоянное значение:
Рис. 5. Иллюстрация поверхности постоянной энергии в сосуде,
которой является цилиндр.
Здесь же дивергенция вектора 
характеризуется через
геометрию линий тока: величина 
в каждой точке потока
крови равна средней кривизне конгруэнции линий тока с точностью до знака.
Величина равна нулю тогда и
только тогда, когда конгруэнция линий тока крови является минимальной
конгруэнцией.
В дальнейшем, поверхности постоянной полной энергии будут характеризоваться
постоянством модуля вектора скорости крови.
В случае ламинарного движения крови
по поверхностям постоянной полной энергии гемодинамическое давление принимает
постоянное значение в рассматриваемом участке сосуда тогда и только тогда,
когда равнодействующая всех сил, действующих на частицы данного участка,
ортогональна стенкам сосуда.
Турбулентное движение крови, линии тока,
скорости которой являются винтовыми линиями, изучается с использованием
плоского распределения.
Пусть все винтовые линии лежат на соосных
цилиндрах (рис. 6):
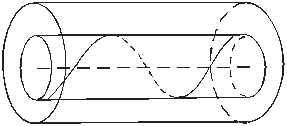
Рис. 6. Иллюстрация винтовой линии, расположенной на
цилиндре.
Геометрия данного вида турбулентного
движения крови изучается на основе геометрии плоского распределения. На основании
приведенных рассуждений, показано: стационарное движение крови является
турбулентным, линии тока которого являются винтовыми линиями тогда и только
тогда, когда вектор скорости крови ортогонален плоскому распределению.
При ламинарном движении частицы крови
движутся по соосным цилиндрам, на каждом из которых скорость крови постоянна.
Все частицы крови, лежащие в плоскости, ортогональной оси сосуда в некоторое
начальное время, а по истечению некоторого единичного времени, будут лежать на
поверхности параболоида. С геометрической точки зрения с этими поверхностями
связываются определенные геометрические объекты, которые позволяют описать ламинарное
движение крови и геометрию такого
движения по участку сосуда (рис. 7):
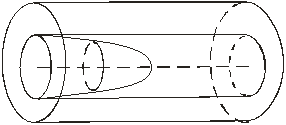
Рис. 7. Профиль скорости крови в сосуде.
Показывается, что цилиндры являются
поверхностями постоянной полной энергии. Для выяснения геометрической природы
параболоида с каждой точкой оси сосуда связывается плоскость, ортогональная
вектору скорости. Интегральные линии вектора скорости будут прямыми.
Доказывается, что полученное распределение будет голономным.
Интегральным многообразием распределения является параболоид, ось которого совпадает с
осью сосуда при ламинарном движении крови по сосуду.
Пусть геодезическая линия с вектором 
образует угол s. Тогда ее уравнения принимают вид:
w 3 = 0
ds +
r = 0.
Для удовлетворения всем условиям и
уравнениям, которые накладываются на движение крови, полагаем:
= x w 1 + h w 2 + (L + 
)w 3
0 = (h + N sins) w 1 – (x + N coss) w 2 + z w 3,
(5)
где L = p 2 sin2 s + (p 1 – q 2) sins coss - q 1 cos2s, N = p3 sins - q3 coss, а x, h, z - неизвестные функции, которые выбираются таким
образом, чтобы удовлетворялись условия интегрируемости приведенных уравнений.
Результаты четвертой главы позволяют
обрабатывать информацию движения крови в отдельно взятом сосуде, основываясь на
его геометрических свойствах.
В пятой главе рассматриваются задачи
по созданию теории, основанной на свойствах субпроективных пространств, для обработки
информации и анализа состояния ССС, разработке математического аппарата и
получения необходимых уравнений движения. Субпроективное пространство,
геометрия которого ассоциируется со структурой ССС, здесь отнесено к голономным
реперам. В начале главы приводятся аргументы в пользу изучения ССС,
основывающейся на пространственном подходе, то есть на изучении структуры ССС,
как геометрии субпроективного пространства. Проводятся аналогии между
структурными свойствами сердечно-сосудистой системы человека и свойствами
субпроективного пространства, а также показывается эффективность использования
субпроективного пространства при изучении структуры системы кровообращения
человека (рис. 8).
В данной главе рассматривается случай, при
котором форменные элементы крови, представляемые как материальные точки и
называемые частицами крови, движутся по поверхностям. Поэтому реперы берутся голономные и это позволяет вводить поверхности, по
которым происходит движение частиц крови. Данный подход позволяет использовать
разработанный в работе математический аппарат для изучения и обработки
информации о движении крови в рамках всей системы кровообращения.
Рис. 8. К иллюстрации соответствия
между структурой ССС и субпроективным пространством.
Далее, вычисляются дифференциальные
операторы для субпроективного пространства, отнесенного к голономным реперам.
Оператор градиента имеет вид, аналогичный
виду этого же оператора в евклидовом пространстве. Для нахождения дивергенции,
получаем:
(6)
где 
В результате
чего получаем:
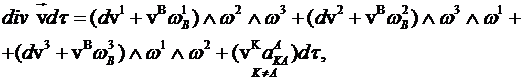
где
в последнем слагаемом вначале производится суммирование по A, а затем
сумма по K ¹ A.
Ротор вектора скорости крови будет
находиться из следующего равенства:
Последнее равенство рассматривается и в ортогональном репере:
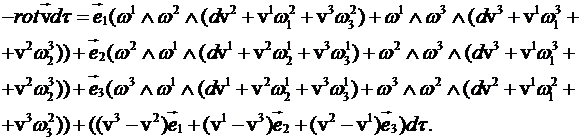
Выражения для нахождения компонент вихря,
будут иметь следующий развернутый вид:
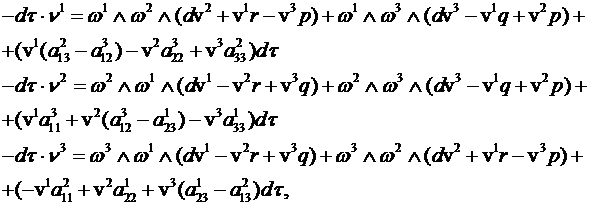
где
dt = w 1Ù w 2Ù w 3 – элемент объема в каждой положительно ориентированной
карте U.
Уравнение неразрывности потока крови имеет
здесь следующий вид:
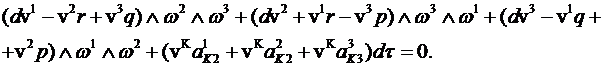
Выбирая
вектор по направлению
касательной линии тока крови, получим:
.
Тогда будем иметь:
.
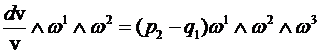(7)
Пусть 
, тогда 
, где v
–модуль вектора скорости.
Уравнение неразрывности в этом случае
имеет вид:
p3sins - q3 coss =0. (8)
Выводятся обобщенные уравнения
Гельмгольца, которые имеют вид:
(9)
и
для случая симметричности векторов 
по нижним индексам,
совпадают с аналогичными уравнениями, для евклидова пространства.
На основании результатов пятой главы
обрабатывается информация для анализа состояния ССС, когда форменные элементы
крови движутся по поверхностям.
В шестой главе создана теория обработки информации кровотока
для анализа стационарного движения крови в субпроективном пространстве, отнесенном
к неголономным реперам, то есть в самом общем случае.
Уравнение неразрывности потока крови
приводится к виду:
,
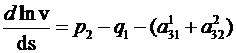(10)
где
вектор скорости сонаправлен с вектором 
.
На основании последних утверждений
получаем: в каждой точке потока крови логарифмическая производная от величины
скорости по направлению линии тока, равна средней кривизне конгруэнций линий
тока крови.
Величина скорости потока крови в
субпроективном пространстве, отнесенном к неголономным реперам, постоянна вдоль
некоторой линии тока тогда и только тогда, когда данная линия представляет
собой линию, принадлежащую минимальной конгруэнции.
Находятся компоненты вихревого вектора для
данного вида субпроективного пространства.
Отношение проекции вихря на касательную
линии тока крови к величине скорости крови есть инвариант линии тока крови,
который пропорционален квадратному корню из разности полной и гауссовой
кривизны линии тока крови.
В седьмой главе рассматриваются вопросы
по использованию геометрических характеристик кровеносной системы в обработке
информации и анализа состояния этой системы.
По
геометрии движения крови в сердце можно характеризовать и сердечные шумы,
которые имеют значение для оценки гемодинамики и для характеристики клапанного
аппарата сердца.
В зависимости от гемодинамических
изменений, вызванных тем или иным пороком сердца, изменяется форма шума, а
также геометрическая конструкция для данного вида движения крови. Под
геометрической конструкцией здесь понимается геометрический объект, применяемый
для изучения данного вида движения: в голономном случае – это поверхность, в
каждой точке которой есть касательная плоскость и нормаль; в неголономном
случае – распределение и нормаль к нему, интегральные линии которого как могут
образовывать конгруэнцию, так и могут не образовывать.
Исследование шумов и тонов сердца на фонокардиограмме дает в руки как исследователя, так и лечащего врача, ценные данные
о состоянии геометрической картины движения крови. Степень отклонения этой
картины от нормы для дифференциального диагноза пороков сердца, позволяет
делать оценку степени анатомического поражения клапанного аппарата сердца и
уточнять в каждом отдельном случае особенности внутрисердечной гемодинамики.
Корректировка геометрического объекта позволяет выявлять изменения в работе
сердечной мыщцы или клапанов, которые привели именно к данному геометрическому
объекту и переход к геометрическому объекту, соответствующего состоянию в
норме, позволяет также проводить корректировку возникших изменений.
Используя
разработанную в данной работе геометрию ССС как в целом, так и ее отдельных
частей и используя шумы и тоны сердца можно выявлять на ранней стадии
патологические изменения как непосредственно в сердце, так и в кровеносной
системе.
Всей
системе кровообращения в модели соответствует две системы геодезических линий,
проходящие через неподвижную точку. Две рассматриваемые системы, представляющие
собой большой и малый круги кровообращения, имеют общую точку – неподвижную
точку субпроективного пространства. Приведенные рассуждения наглядно
продемонстрируем в виде блок-схемы модели ССС и изображены на рис.9. Представленная
на рисунке блок-схема является более
формальным воплощением представляемых ранее подходов, лежащих в основе
моделирования деятельности ССС при пространственном подходе. Более того, данная
блок-схема хорошо согласуется с ранее представляемыми формализациями системы
кровообращения, полученными различными авторами.
В
процессе развития и накопления знаний по
физиологии и патофизиологии данная
модель может постоянно усовершенствоваться. Разнообразие свойств ССС, возможных
гипотез по регуляции и по патологическим изменениям, столь обширно, что
отразить их в рамках одной модели довольно сложно. Предлагаемая методология
обработки информации по состоянию ССС позволяет это делать, не разрабатывая при
этом новой модели для каждой конкретной задачи.
Возможно введение в модель и патофизиологических изменений. Патофизиологические
изменения могут быть заданы изменением соответствующих видов движений. При
переходе к таким изменениям начинают появляться завихрения, которые не
свойственны состоянию участка сосуда или всей системы в норме. Геометрически
это представимо тем, что в норме с каждой точкой сосуда связан один
геометрический объект, а при патофизиологических изменениях с этой же точкой
будет связан другой геометрический объект. Такие переходы как в одну, так и в
другую сторону могут быть реализованы в предлагаемой модели с использованием
патофизиологических и морфометрических данных клиники.
Существующие до сего момента системы поддержки принятия решений
(СППР), содержащие системы по диагностике ССС, а также нарушения в кровообращении
беременных женщин, не решают на доступном для каждого врача уровне
поставленных задач по эффективной и не
дорогой диагностике. Поэтому была
предложена структура программного и математического обеспечения СППР,
включающая в себя не только задачи диагностики, но и поддерживает решение задач
по прогнозированию, диагностике изменений в ССС, профилактику и возможные пути
коррекции по устранению дефектов в кровеносной системе.
МКК
БКК
Рис. 9. Блок-схема модели ССС.
С
– сердце; МКК и БКК – малый и большой круги кровообращения; А – дуга аорты; АТ
– артерии, ТТ – капилляры, ВТ – вены нижней части тела
и ног; АГ – артерии, ТГ – капилляры, ВГ – вены головы и рук; ЛА – легочная
артерия; ЛК – легочные капилляры; ЛВ – легочная вена.
В системе реализован алгоритм
управления процессами контроля и диагностики состояния ССС, схема которого
представлена на рис.10. Алгоритм работает следующим образом. Для обследования
состояния ССС используется доплеровский фонендоскоп (ДФ). Далее, данные,
полученные для обследуемого сравниваются с табличными.
Если при сравнении полученных значений скоростей и индексов
нет расхождений с табличными, то причину недуга нужно искать в другом или это
является условием отсутствия отклонений в ССС. При обнаружении у
пациента расхождений с табличными данными либо ДФ подключается к персональному
компьютеру (ПК) для проведения дальнейших исследований, либо при обнаружении
существенных расхождений констатируется наличие патологических изменений в ССС
с организацией лечебно-оздоровительных мероприятий. При подключении ДФ к ПК, на
экране которого появляется график зависимости кровотока от времени и на
основании разработанного в работе математического обеспечения (МО) для
обработки информации состояния ССС методами дифференциальных форм, делаются
выводы о наличии в сосуде турбулентного движения. Последний вид движения крови
в большинстве случаев не свойственен сосудам в норме и позволяет говорить о
патологических изменениях. В основе МО лежат результаты глав
4 и 5, в которых получены геометрические характеристики для ламинарного и
турбулентного движений крови. В качестве геометрических характеристик в
МО выступают различного вида распределения, дифференцируемые отображения,
интегральные линии и т.п. По этим геометрическим характеристикам на экране
монитора появляются графики зависимости кровотока от времени, и с помощью
метода цветового доплеровского картирования приводится анализ частотных
спектров. Это позволяет выявлять виды движений крови в сосуде и выделять виды
движений, которые не являются для данного сосуда нормой. Применение МО не возможно
без полученных уравнений движения крови. Выведенные на экран монитора виды
движения крови (ВДК) либо не подтверждают диагноз наличия патологических
изменений и необходимы другие лечебно-диагностические мероприятия, либо диагноз
подтвержден и необходимо проведение лечебно-оздоровительных мероприятий для
ССС.
Рис. 10. Алгоритм управления процессами
контроля и диагностики состояния ССС.
Отличительной особенностью предлагаемой
автоматизированной системы является требование наличия в ней нестандартного
математического обеспечения для выявления турбулентного движения на ранней
стадии его появления.
Структурная схема предлагаемой системы
поддержки принятия решений приведена на рис. 11. В этой системе информация о
патологических изменениях в ССС вводится в ПК с помощью доплеровского
фонендоскопа через соответствующие драйверы связей (ДС). Поступающая внешняя
информация структурируется в виде файла исходных данных (ФИД). Далее информация
о состоянии ССС из ФИД передается на вход блока традиционного принятия решения
(БТПР), работа которого заключается в получении с помощью ДФ числовых
характеристик движения крови. Кроме этого на БТПР передается информация об
изменениях ССС с интерфейса пользователя.
Далее информация поступает в блок анализа
(БА), где анализируется ситуация по поводу расхождения полученных данных с
табличными и выносится решение либо на интерфейс пользователя о наличии или
отсутствии патологии, либо информация поступает для обработки в блок работы
алгоритма управления процессами контроля и диагностики (БРАУПКД) состояния ССС.
По информации, получаемой в результате
работы БРАУПКД, блок определения диагноза (БОД) под управлением
врача-исследователя формирует параметры для проведения курса лечения.
В базе
данных (БД) находится электронные медицинские карты (ЭМК) пациентов, виды
движения крови (ВДК) в ССС в норме и патологии, числовые значения для скорости
крови, справочные данные по заболеваниям и другая справочная информация.
Из банка
модулей движения крови пользователь может извлечь модель турбулентного и
ламинарного движений крови. С помощью блока «раскраски» этих
моделей (БРМ) получаем светлые цвета для ламинарного и более темные для
турбулентного движений крови. Это позволяет наглядно наблюдать за изменением
видов движения крови вдоль сосуда и рационально планировать лечение, как
сосудистых заболеваний, так и сопутствующих заболеваний.
С помощью
интерфейса пользователя врач может наблюдать: временные фрагменты измеряемых
параметров, графики зависимости скорости от времени, окрашенность участков
сосуда, отражающих ВДК; и т.д. Это позволяет точно определять места в сосуде,
где произошли патологические изменения, и далее активно исследовать это место.
Рис.11. Структурная схема СППР врача сосудистого
хирурга (флеболога).
На рис. 11
приняты следующие сокращения: ДФ – доплеровский фонендоскоп; ДС – драйвер
связи; ФИД – файл исходных данных; БТПР – блок традиционного принятия решения; БА
– блок анализа; БРАУПКД – блок работы алгоритма управления процессами контроля
и диагностики; БПД – блок постановки диагноза; БД – база данных; БРМ – блок раскраски
моделей движений крови.
Приведенная схема системы принятия решений сосудистого хирурга (флеболога)
позволяет с высокой степенью точности констатировать наличие у пациента
патологических изменений в ССС. Результаты данных исследований были
подтверждены квалифицированными врачами с использованием, как дорогостоящей
аппаратуры, так и в результате проведения лечебных мероприятий. Более того,
получение на экране монитора графиков, характеризующих зависимость кровотока от
времени, базируется на разработанном математическом аппарате. Адекватность
предлагаемого математического аппарата для обработки информации о движении
крови проводится в три этапа. Первый этап предполагает получение аналитических
выражений, совпадающих с общепринятыми теоретическими выкладками и получение
известных положений, которые являются следствиями полученных в работе теорем.
Второй этап – это проведение экспериментальных исследований для подтверждения
возможности применения в качестве теории данного подхода обработки информации
при анализе состояния ССС, позволяющей решать конкретные медицинские задачи. И
третий этап – заключения высококвалифицированных медицинских специалистов.
На
основании информации, получаемой от БТПР, БПД и дополнительной информации из БД
и со стороны интерфейса пользователей, вырабатываются рекомендации по
проведению профилактических, терапевтических или хирургических мероприятий,
которые через интерфейс пользователя передаются врачу в качестве рекомендаций
по ведению пациента.
В базе
данных хранится медицинская карта пациента в электронном виде, в которой
находятся его паспортные данные, данные анамнеза, итоги осмотров, опросов,
экспериментальных исследований, диагностические заключения, и т.д.
Для проверки достоверности и эффективности
обнаружения дефектов в системе кровообращения с использованием обработки
информации состояния этой системы методами дифференциальных форм, были обследованы
пациенты сосудистого хирурга, а также женщины в возрасте от 17 до 41 года с
неосложненным течением беременности и с фетоплацентарной недостаточностью. В
ходе проведения обследований были выделены два класса: Первый класс (ω0)
– люди без патологических изменений в ССС и второй класс (ω1) –
люди, у которых такие изменения обнаружены.
Проверка репрезентативности полученных
выборок осуществлялась на основе формулы расчета объема выборок для задач классификации
по заданной величине ошибки. При уровне достоверности 0,1 получили, что выборки
будут достоверными, если 
= 121 человек и = 105 человек. Первоначальные обследования проводились с
использованием ультразвуковых анализаторов без
разработанного математического аппарата.
Расчеты соответствующих показателей
проводятся с использованием следующей таблицы 1.
Таблица 1
Распределение
результатов наблюдений
|
Обследуемые |
Результаты исследований |
Всего |
|
|
Наличие дефектов |
Отсутствие дефектов |
||
|
Количество
обследуемых класса ω1 - nω1 |
Истинно (ИП) |
Ложно (ЛО) |
ИП
+ ЛО |
|
Количество обследуемых
класса ω0 - nω0 |
Ложно (ЛП) |
Истинно (ИО) |
ЛП
+ ИО |
|
Всего |
ИП + ЛП |
ЛО + ИО |
ИП
+ ЛП+ЛО+ИО |
В таблице
приняты следующие обозначения:
ИП – истинно-положительный результат, который равен
количеству людей с обнаруженными патологическими изменениями в ССС;
ЛП – ложноположительный результат, который
соответствует количеству здоровых людей, у которых были обнаружены изменения;
ЛО – ложноотрицательный результат, равный количеству
людей с дефектами, у которых дефекты не обнаружены;
ИО – истинно-отрицательный результат, численно
равный количеству здоровых людей, у которых дефекты не обнаружены.
Определим
основные характеристики для оценки эффективности проводимых исследований.
Диагностическая
чувствительность (ДЧ) обнаружения дефектов в системе кровообращения с
использованием ультразвуковых анализаторов по отношению к классу ω1,
задается отношением количества пациентов с истинно-положительным результатом к
количеству больных, т.е.
ДЧ = 
(11)
Или в процентном отношении
ДЧ
= 
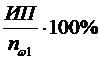(12)
Диагностическая
специфичность (ДС) обнаружения дефектов ССС по классу ω0
есть отношение ИО результатов к количеству здоровых людей:
ДС =
или ДС =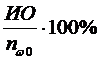
(13)
Предсказательность (прогностическая значимость)
положительных результатов ПЗ+ определяется формулами:
ПЗ+ =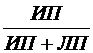 
или ПЗ+ = 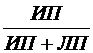·100% (14)
Предсказательность (прогностическая значимость) отрицательных
результатов ПЗ- задается формулами:
ПЗ- =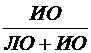 
или ПЗ- = 
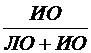·100% (15)
Диагностическая эффективность (ДЭ)
определяется равенствами:
ДЭ =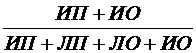 
или ДЭ = 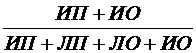·100% (16)
Для контрольных выборок полученные
результаты представлены в таблице 2.
Таблица 2
Распределение
результатов обнаружения дефектов в ССС ультразвуковыми анализаторами
|
Обследуемые |
Результаты исследований |
Всего |
|
|
Наличие дефектов |
Отсутствие дефектов |
||
|
nω1 = 150 |
128 |
22 |
150 |
|
nω0 = 150 |
28 |
122 |
150 |
|
Всего |
156 |
144 |
300 |
На основании данной таблицы находятся введенные выше
величины.
Чувствительность равна ДЧ = 128/150 = 0,85. Специфичность составляет ДС
= 122/150 = 0,81. Предсказательность положительных
результатов равна ПЗ+=0,82. Предсказательность отрицательных результатов ПЗ-=0,85.
Диагностическая эффективность равна ДЭ = (128+122)/300 = 0,83.
Сводные
показатели качества обнаружения дефектов в ССС с помощью ультразвуковых
анализаторов без применения специального математического аппарата представлены
в виде таблицы 3.
Таблица 3
Таблица
показателей качества с использованием ультразвуковых анализаторов
|
Показатель |
ДЧ |
ДС |
ПЗ+ |
ПЗ- |
ДЭ |
|
Значение показателя |
0,85 |
0,81 |
0,82 |
0,85 |
0,83 |
Анализ
таблицы 3 показывает хорошее совпадение результатов экспертного оценивания и
проверки качества обнаружения дефектов в ССС с помощью ультразвуковых
анализаторов.
Дополнительные контрольные выборки были
сформированы из людей, у которых исследования по обнаружению дефектов ССС
проводились с использованием предложенной в работе модели системы
кровообращения с использованием геометрии субпроективных пространств и
разработанного математического аппарата. Заполним таблицу 4, аналогичную
таблице 2.
Таблица 4
Распределение
результатов обнаружения дефектов в ССС с использованием математического
аппарата
|
Обследуемые |
Результаты исследований |
Всего |
|
|
Наличие дефектов |
Отсутствие дефектов |
||
|
nω1 = 110 |
105 |
5 |
110 |
|
nω0 = 110 |
7 |
103 |
110 |
|
Всего |
112 |
108 |
220 |
По данным
последней таблицы рассчитываются показатели качества обнаружения дефектов ССС
на основании обследований пациентов доплеровскими фонендоскопами с привлечением
специально разработанного в данной работе математического аппарата.
ДЧ =
105/110 = 0,95 ПЗ+
= 105/(105 + 7) = 105/112 = 0,94
ДС =
103/110 = 0,94 ПЗ-
= 103/108 = 0,95
ДЭ = (105
+ 103)/(112 + 108) = 208/220 = 0,95
Сводная
таблица по показателям качества в этом случае представлена таблицей 5.
Таблица 5
Таблица
показателей качества с использованием ультразвуковых анализаторов и методов
геометрии субпроективных пространств
|
Показатель |
ДЧ |
ДС |
ПЗ+ |
ПЗ- |
ДЭ |
|
Значение показателя |
0,95 |
0,94 |
0,94 |
0,95 |
0,95 |
Сравнивая таблицы 5 и 3, получаем увеличение
показателей качества определения дефектов в ССС при использовании методов
геометрии субпроективных пространств, которые приведены в таблице 6.
Таблица 6
Сводная
таблица показателей качества
|
Увеличение показателя |
ΔДЧ |
ΔДС |
ΔПЗ+ |
ΔПЗ- |
ΔДЭ |
|
Численное значение |
0,1 (10%) |
0,13 (13%) |
0,12 (12%) |
0,1 (10%) |
0,12 (12%) |
Среднее
улучшение качества обнаружения дефектов по всем показателям достигает величины
11,4%.
Адекватность модели сердечно-сосудистой системы является одним из факторов
по обнаружению заболеваемости и предупреждению развития кардиологических
патологий.
В
диссертации присутствуют три этапа доказательства адекватности.
Во-первых, при разработке математического аппарата получались аналитические
выражения, совпадающие с общепринятыми теоретическими выкладками.
Во-вторых, в ходе экспериментальных исследований показана эффективность
применения разработанных теоретических основ для решения конкретных медицинских
проблем.
И,
в-третьих, показано соответствие теоретических и экспериментальных данных. Продемонстрируем
это соответствие более подробно.
Изменение площади поперечного сечения сосуда сказывается на таких
характеристиках траекторий движения частиц крови как их полная и гауссова
кривизна. Поэтому эластичность сосуда с геометрической точки зрения характеризуется
этими понятиями.
Зависимости сечений сосудов от трансмурального давления нелинейны и для
большей наглядности построим графики зависимостей сечения от давления по
теоретическим данным, полученным в работе, и сравним их с экспериментальными
данными (рис. 12).
Ввиду
того, что разность между полной
и гауссовой кривизнами есть некоторый инвариант K – 
, то для каждого сосуда этот инвариант будет
сохранять конкретное значение. Это позволяет аппроксимировать эластичность сосудов
в виде зависимости для площади поперечного сечения сосуда:
,
где Δp – трансмуральное давление,
S
– экспериментально определяемая площадь поперечного сечения
сосуда при Δp = 1·10
.
Последняя
формула дает удовлетворительные совпадения с экспериментальными данными при
значении коэффициентов: для легочной артерии K – K
=3,28; a = 16,87·10 ; b = 6,398·10
; для полой вены K – K = 1,6; a = 1,5 ·10; b = 1·10.
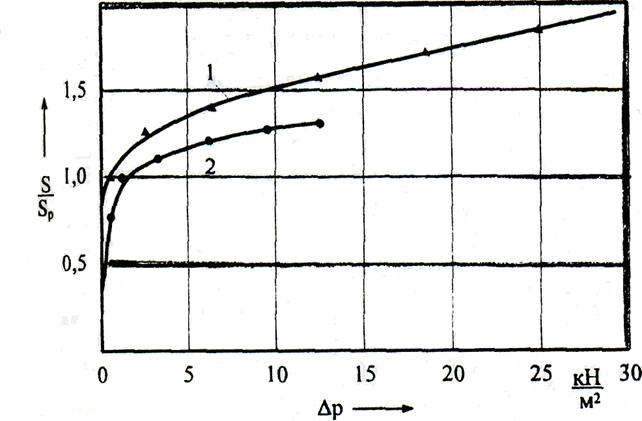
●▲ – экспериментальные данные по
монографии Дворецкого Д.П. и Ткаченко Б.И. «Гемодинамика в легких».
- теория, 1 – легочная артерия; 2 – полая вена.
Рис. 12. Зависимости сечений сосуда от трансмурального
давления.
Формула
для S описывает зависимость поперечного сечения сосуда от трансмурального
давления для сосудов эластического типа. Здесь же выражается зависимость между
кривизной линий, по которым движется кровь, и эластичностью сосудов.
Эластичность со структурной точки зрения характеризуется кривизной линий, по которым
движется кровь. Эта кривизна определяется в пространстве, в котором изучается
структура данного сосуда.
Далее,
для доказательства адекватности математической модели сосудистой системы
возьмем малый круг кровообращения. Для сравнения теоретических и
экспериментальных данных удобнее использовать приведенные относительные
величины, так как условия проведения опытов и сами объекты экспериментов различны.
В
качестве характеристик, определяющих состояние сосудистой системы, рассмотрим
зависимость легочного артериального давления от объемного кровотока в
стандартном состоянии, а это соответствует опытам на изолированных
перфузируемых легких, прокачиваемых кровью с постоянным расходом. Ввиду того,
что вариации значений суммарного кровотока существенны, то для сохранения
методических условий сопоставимости теоретических результатов с
экспериментальными, удобно в качестве независимого параметра принять отношение
значения объемного расхода к максимальному.
Сравнение
данных экспериментальных исследований с результатами моделирования проводилось
при следующих значениях величин:
1) давление окружающей среды –
1,03·10 Па (
2) плотность крови – 1,274·10
;
3) вязкость крови – 0,002 Пас;
4) соотношение расхода в
состоянии покоя к максимальному 
= 0,2
( 
= 367·10
)
5) коэффициент 
= 2,1; 
= 1,3.
Тогда
зависимости артериального давления от кровотока при фиксированных значениях
венозного давления обладают удовлетворительной степенью совпадения
количественных показателей состояния с экспериментальными данными (рис. 13).
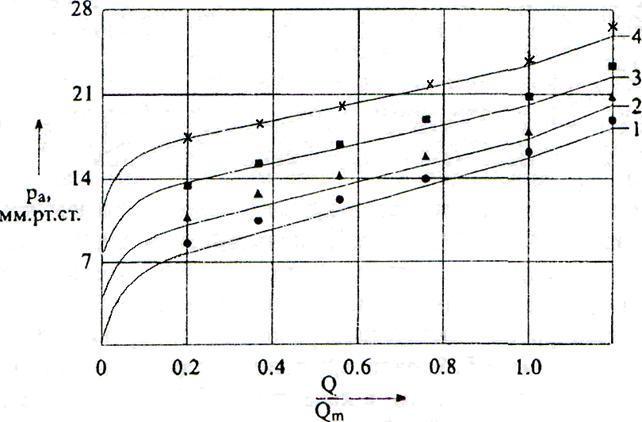
●▲ ■ – экспериментальные данные из
монографии Вербеля Э.Р.
- теория
1 - ● p
= = =
4 - × p =
Рис. 13. Зависимость артериального
давления от кровотока при фиксированных значениях венозного давления.
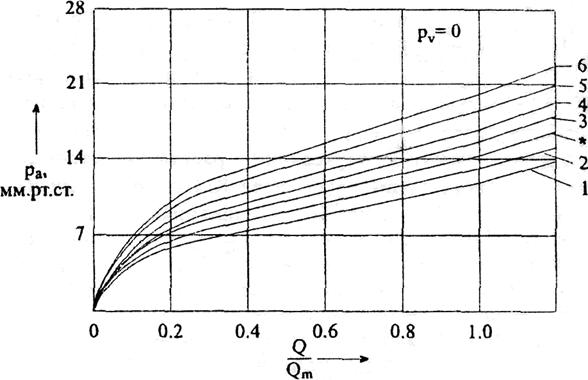
Влияние на сосудистую систему изменения вязкости крови хорошо согласуется
с опытными данными
и будет иметь следующий вид:
*- вязкость крови η =
0,002 Пас (норма)
1, 2, 3 – снижение вязкости
соответственно на 30%, 20%, 10%
4, 5, 6 – повышение вязкости
соответственно на 10%, 20%, 30%.
а)
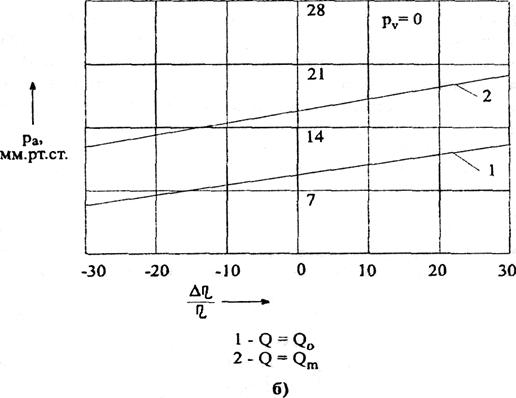
Рис.14.
Исследование влияния на сосудистую систему изменения вязкости крови.
Изменение вязкости крови не компенсируется внутренней «автоматикой»
рассматриваемой системы, что проявляется в повышении или понижении артериального
давления в зависимости от соответствующего изменения вязкости (рис. 14б).
Результаты зависимостей между величинами показаны на данных рисунках и демонстрируют
хорошее совпадение теоретических и экспериментальных данных. Это является
доказательством адекватности предложенной модели сердечно-сосудистой системы.
Восьмая
глава посвящена экспериментальному подтверждению полученных теоретических
результатов. Предложена структура по принятию решений при формализованном
описании ССС человека в задачах анализа, получения информации и управления при
диагностике состояния исследуемой системы. Показано, что применение
разработанного в диссертации математического аппарата при диагностике состояния
ССС с помощью ультразвуковых анализаторов, дает среднее улучшение качества
обнаружения дефектов по всем показателям на 11,4 %.
В ходе экспериментов подтверждаются полученные теоретические результаты.
Методом
цветового доплеровского картирования (Фурье-преобразование с разложением по
цветовым потокам) проводится анализ частотных спектров. Ламинарные потоки имеют
низкие скорости и во всех фазах кровотока имеют постоянное значение скорости.
Меньшие значения скорости соответствуют слоям, граничащим со стенками сосуда.
Для турбулентных потоков значения скорости частиц в фазе турбулентности
различны. Внутри такого потока вектор скорости разлагается на составляющие и поток имеет «разреженный» хаотичный характер.
Внутри потока отмечается зависимость частоты от амплитуды мощности потоков.
Подтверждением эффективности применения
данного метода по обнаружению бляшек в кровеносных сосудах является таблица 7,
где получена для данного метода наибольшая эффективность R = 0,1.
В заключение
работы подводится итог основных результатов, касающихся разработки
непротиворечивой и логически выверенной теории для обработки информации
состояния ССС человека, которые в совокупности с исследованиями по
дифференцируемым отображениям и по различного вида движениям крови по участку
сосуда, позволяют более эффективно использовать анализ, основанный на
геометрической картине движения крови как по всей ССС, так и по ее отдельному
участку. Все вышесказанное обеспечивает повышение точности диагностики
появления патологических изменений в сосудах и как следствие своевременно
назначить лечение.
Подтверждением вышесказанного является таблица 7, в которой приводится
сопоставительный анализ известных и предлагаемых методов исследования на задаче
обнаружения патологических изменений сосудов:
,
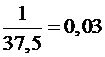
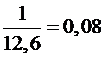
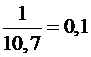
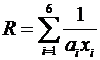