Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 17. -

Вып. 2. - 2018. - URL:

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/TITL.HTM

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-58-html/TITL-58.htm

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-58-html/cont.htm

 

УДК 004.421.2:519.178.

 

Поиск времени, необходимого для преодоления расстояния из пункта «а» в пункт «Б»

 

Ó 2018 г. Ковалев В. А.

 

(kovalev.doc)

 

В работе рассматривается новый подход к поиску времени, необходимого для перемещения из одного заданного пункта в другой в условиях предметной области на примере логистики внутри города. На практике зачастую оказывается, что кратчайший путь не является самым быстрым, так как не было учтено множество факторов, влияющих на скорость перемещения.

Ключевые слова: кратчайший путь, графы, математическое ожидание, математическая статистика.

 

На данный момент существует множество алгоритмов по нахождению кратчайшего пути. Примерами могут служить алгоритмы Дейкстры, Флойда­­­-Уоршалла, Беллмана и т.д. [1] Каждый из них выполняет свою абстрактную задачу на графах. Но самое интересное, что результаты их работы не всегда имеют отношение к действительности. Для наглядности приведем простую задачу.

Дан неориентированный граф (рис. 1), рёбра которого – расстояния в километрах между населёнными пунктами некоторой местности. Необходимо найти кратчайший путь от пункта А до пункта В.

 

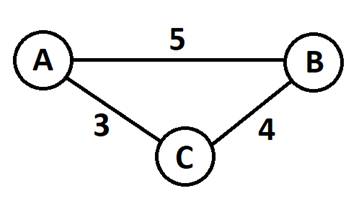
Рис. 1

 

Решение задачи кажется очевидным: ребро АВ с весом (расстоянием) 5. Если рассматривать эту задачу, сформулированную в таком виде в учебнике по информатике или математике, то ответ верен. Но на практике это не всегда так. Представим, что данный граф является моделью конкретного участка дороги, где есть светофоры, пешеходы, неровности. Решение уже не будет выглядеть так тривиально. Введём для каждого участка следующие параметры:

·                   S – длина участка в километрах

·                    – максимальная скорость, разрешённая на данном участке

·                   t – время, необходимое для преодоления данного участка пути

·                   K – качество дороги

·                   n – количество нерегулируемых пешеходных переходов

·                    – поток пешеходов на i – ом нерегулируемом пешеходном переходе в человек/час.

·                   m ­– количество регулируемых пешеходных переходов

·                   tк i – время работы красного сигнала i-ого светофора

·                   tз i – время работы зелёного сигнала i-ого светофора 

·                    – время, необходимое пешеходу для перехода дороги

·                    – суммарное время, затраченное на остановки

 

Сразу сделаем несколько замечаний. Обратим внимание, что величина K –  абстрактная величина и может меняться от 0 (движение невозможно) до 1 (идеально ровный асфальт). Также будем считать, что время, требуемое для разгона и торможения, сравнительно мало и им можно пренебречь. Исходя из этого, автомобиль на всём участке пути движется со скоростью .

Будем искать для каждого участка необходимое для его преодоления время t по следующей формуле:

 

 

Определим формулу для остановок, которые должен сделать на своём пути автомобиль. Очевидно, что оно равно сумме времён, затраченных на остановки на регулируемых и нерегулируемых пешеходных переходах:

 

 

С помощью формул математической статистики [2] можно легко рассчитать математическое ожидание времени, которое простоит водитель в ожидании зелёного сигнала светофора. Для каждого светофора оно будет находится следующим образом:

 

 

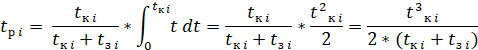
Следовательно, легко найдём время остановок на регулируемых переходах:

 

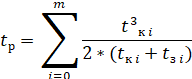
Для того, чтобы смоделировать ситуацию на нерегулируемом пешеходном переходе достаточно понять, что она идентична предыдущей ситуации. Время, которое будет затрачено на переход дороги пешеходом, и есть искомое время, которое водитель не едет. Только поток можно уменьшить вдвое, так как необходимо ждать всё время, пока идёт пешеход, а достаточно только его пропустить.  То есть в данной ситуации:

 

 

В результате получаем аналогичную формулу:

 

 

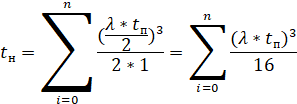
И конечная формула будет иметь следующий вид:

 

 

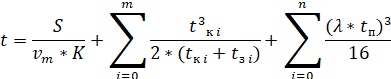
Если мы будем сравнивать не , то задача уже не выглядит такой простой. При определённых параметрах путь через вершину С окажется быстрее. Например, если параметры будут такими же, как в приведённой ниже таблице:

 

Параметр

AB

AC

CB

S

5

3

4

60

60

60

40

40

40

0,01

0,01

0,01

К

0,6

0,8

0,9

0,03

0,03

0,03

0,03

0,03

0,03

n

2

1

0

m

1

0

1

 

то получится противоположный результат:

 

 

На примере конкретной задачи, мы получили интересный результат. Таким образом, более короткий путь в действительности не всегда оказывается кратчайшим.

 

Литература

 

1.     Axo Альфред, В., Хопкрофт Джон, Ульман Джеффри, Д. Структуры данных и алгоритмы: Пер. с англ. - М.: Издательский дом "Вильяме", 2003. - 384 с.: ил. - Парал. тит. англ. ISBN 5-8459-0122-7 (рус.)

2.     Козлов М. В., Прохоров А. В. Введение в математическую статистику. - М.: Изд-во МГУ, 1987. - 264 с.

 

SEARCH FOR THE TIME WHICH IS NECESSARY FOR OVERCOMING THE DISTANCE FROM ITEM "A" TO ITEM "B"

 

Kovalev V. A.

 

The paper considers a new approach to time search, which is necessary for moving from one given point to another in the context of the subject area, using the example of logistics inside the city. In practice, it often turns out that the shortest path is not the fastest since many factors affecting the speed of movement have not been taken into account.

Key words: shortest path, graphs, mathematical expectation, mathematical statistics.

 

Смоленский государственный университет

wladickowalew@gmail.com

Поступила в редакцию 2.06.2018