Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 17. -

Вып. 2. - 2018. - URL:

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/TITL.HTM

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-58-html/TITL-58.htm

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-58-html/cont.htm

 

УДК 611.718.4(470. 332):312

 

Метрологическая характеристика упрощенного способа измерения угла скрученности бедренной кости человека: оптимизация и планирование измерительного эксперимента

 

© 2018 г. Тейкина О. Ю., Меренков В. Г., Прудников И. М.

 

(teykina.doc)

 

Впервые проведена метрологическая оценка оригинального способа измерения угла скрученности бедренной кости человека. Выполнены вычисление среднего, построение доверительного интервала  с заданным уровнем значимости и оценка числа экспериментов измерения углов скрученности длинных трубчатых костей.

Ключевые слова: бедренная кость, длинная трубчатая кость, эпифиз, диафиз, торсия кости, торсионная трансформация кости, угол скрученности кости.

 

Цель исследования

 

Изучение метрологической характеристики упрощенного способа измерения угла скрученности бедренной кости человека для остеометрических исследований археологического костного материала в местах массовых захоронений.

Материалы и методы исследования

 

Исследования проводились в лаборатории остеологического мониторинга археологических исследований на остеологическом материале из некрополя Пятницкого конца средневекового Смоленска, полученном при проведении охранных раскопок ИА РАН 2008-2009 гг. на ул. Студенческой г. Смоленск. Кости человеческих скелетов раскопе из разных горизонтов погребений раскопа, при поступлении в лабораторию были перемешаны, ссыпаны хаотично в мешки для строительного мусора, неочищены, с большим количеством почвы. Силами сотрудников лаборатории была создана систематизированная коллекция длинных трубчатых костей человека, введенная в 2011 г. в научный оборот. Некрополь Пятницкого конца древнего Смоленска по артефактам археологами датирован XII–XVIII веками.

Измерялись углы скрученности бедренных костей человека из коллекции с применением собственного упрощенного способа, сущность которого изложена далее [1-3]. Для измерения бедренной кости используются фиксирующий штатив и строительный уровень для контроля горизонтальности поверхности, имеющий фиксированную ампулу на 00 и поворотную ампулу на 3600 бедренная кость фиксируется в штативе горизонтально (продольная ось диафиза кости совпадает с положением горизонтальной оси) задней поверхностью кости вниз. Линейка строительного уровня устанавливается на вершины задних поверхностей обоих мыщелков кости. Разворотом кости вокруг оси диафиза достигается их строго горизонтальное положение под контролем фиксированной ампулы строительного уровня (рис. 1). Далее линейка строительного уровня устанавливается в положении, совпадающем с линией, сверху зрительно делящей головку и шейку бедренной кости пополам (аналогично уже существующей технике, так как не изменяется при изменении положения анатомического объекта в пространстве) (рис. 2). Угол скрученности кости (угол торзиона) определяется по шкалам поворотной ампулы строительного уровня путем ее вращения до срединного (горизонтального) положения (со знаком «+» или «-» соответственно условиям уже существующей техники) (рис. 3). Измерение торсии левых и правых бедренных костей проводится зеркально, ориентируясь на топографию используемых анатомических ориентиров.

 

 

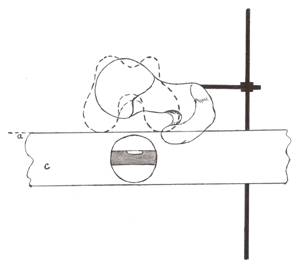
Рис. 1. Измерение угла скрученности бедренной кости по предлагаемой методике. Кость фиксирована горизонтально. Вид сбоку (верхняя поверхность проксимального эпифиза - сплошная линия), нижний эпифиз бедренной кости – пунктирная линия; а – линейка строительного уровня; с – фрагмент строительного уровня с фиксированной ампулой на 00.

 

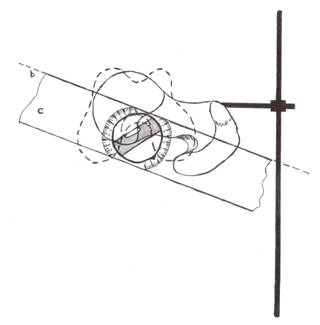
Рис. 2. Измерение угла скрученности бедренной кости по предлагаемой методике. Кость фиксирована горизонтально. Вид сбоку (верхняя поверхность проксимального эпифиза - сплошная линия), нижний эпифиз бедренной кости – пунктирная линия; b – линейка строительного уровня; с – фрагмент строительного уровня с поворотной ампулой на 3600.

 

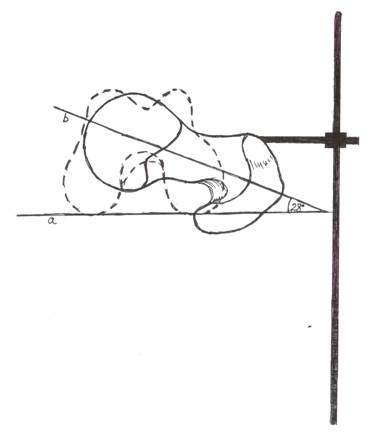
Рис. 3. Результат измерения угла скрученности бедренной кости по предлагаемой методике. Кость фиксирована горизонтально. Вид сбоку (верхняя поверхность проксимального эпифиза - сплошная линия), нижний эпифиз бедренной кости – пунктирная линия; а – линия фиксации строительного уровня к мыщелкам бедренной кости; b – линия фиксации строительного уровня по линии, делящей головку и шейку бедренной кости пополам.

 

В основе примененного способа измерения торсии бедренной кости – общие правила, представленные в запатентованном нами «Способе измерения углов скрученности длинных трубчатых костей», согласно которому угол скрученности определяется как разность углов наклона дистального и проксимального эпифизов по отношению к плоскости горизонта. Кость жёстко закрепляется в горизонтальной плоскости, после чего механическим или электронным уровнем-угломером измеряется угол наклона проксимального и дистального эпифизов кости по отношению к плоскости горизонта. Далее угол скрученности вычисляется как разность углов наклона дистального и проксимального эпифизов. Так как при измерении проксимального эпифиза, измерительный прибор переворачивается на 180o в горизонтальной плоскости, при определении угла скрученности, наклона проксимального эпифиза необходимо брать с противоположным знаком. В результате для определения угла скрученности используется следующая формула:

 

Fс = φд – (-φп) = φд + φп  ,

 

где: Fс - угол скрученности кости, φд – угол наклона к плоскости горизонта дистального эпифиза, φп - угол наклона к плоскости горизонта проксимального эпифиза.

Для упрощения вычислений кость может быть закреплена так, чтобы, например, проксимальный эпифиз располагался строго горизонтально, тогда угол скрученности будет равен углу наклона дистального эпифиза кости по отношению к плоскости горизонта:

 

Fс = φд

 

Необходимые инструменты: фиксирующий штатив и строительный уровень для контроля горизонтальности поверхности, имеющий, фиксированную ампулу на 00 и поворотную ампулу на 3600 .

 

Результаты и их обсуждение

 

Измерены углы скручивания 540 разрозненных бедренных костей скелета человека (из них 264 левых и 276 правых) коллекции длинных трубчатых костей нижних конечностей. Известны различные способы измерения торсий мацерированных длинных трубчатых костей человека, с применением большого перечня инструментов, иногда достаточно дорогостоящих, и сложных многоэтапных действий, требующих специальных навыков персонала исследовательской лаборатории. Очевидно, в таких случаях измерение одного костного объекта занимает длительный промежуток времени, что затягивает остеометрический процесс при наличии большого количества объектов исследования.

В наших исследованиях для измерения углов скрученности бедренных костей применялся собственный способ с использованием простого и доступного для приобретения лабораторного инструментария (штатив, держатель, строительный уровень). Указанные особенности примененного способа измерения углов скрученности выгодно отличают его от других известных способов при большом количестве объектов исследования, как в нашем случае.

 

Оптимизация и планирование измерительного эксперимента

 

Протоколы статистической оценки предложенного способа измерения торсий (углов скрученности)

длинных трубчатых костей

 

Проведено по 60 измерений трех разных трубчатых костей согласно новой методике измерения углов скрученности (таб. 1).

 

Таблица 1

Результаты измерений угла скрученности костей 299 d, 92s, 67s для статистической характеристики предлагаемого способа измерения торсии

 

№кости

/

№изм.

Угол скрученности в град.

299d

92s

67s

1

21

4

8

2

20

5

8

3

20

4

6

4

18

5

7

5

17

7

4

6

18

8

5

7

18

7

6

8

18

7

4

9

16

6

3

10

16

6

2

11

16

6

4

12

17

6

3

13

16

8

4

14

15

8

4

15

19

6

3

16

16

6

2

17

16

10

5

18

16

8

7

19

17

6

4

20

17

8

3

21

18

6

2

22

16

8

3

23

15

7

3

24

18

9

2

25

17

7

3

26

18

4

4

27

19

6

4

28

16

3

7

29

17

5

5

30

19

6

2

31

18

7

6

32

18

6

5

33

19

5

2

34

18

8

4

35

17

7

2

36

19

5

7

37

20

7

5

38

16

5

5

39

16

3

7

40

17

4

3

41

17

5

5

42

16

7

4

43

17

6

7

44

19

6

6

45

17

4

5

46

18

5

7

47

19

4

6

48

18

6

5

49

17

7

6

50

20

6

2

51

18

4

6

52

17

7

4

53

19

3

8

54

16

6

4

55

17

3

7

56

16

7

4

57

18

5

7

58

17

5

6

59

16

7

4

60

20

7

5

                                                    

1. Проверялась идея о нормальности распределения данных с уровнем ошибки α=0,05. Квантиль для нормального распределения N(0,1) с уровнем доверия 0,95 равен 1,96 [9]. Квантиль распределения Стьюдента с n-1 степенями свободы для n=29 и n=59 с уровнем ошибки α=0,05 равен соответственно 2,04 и 2,0 [9].

Проверена гипотеза о нормальности распределения данных для костей при n=30 и n=60 измерений.

Проведено ранжирование данных и подсчет их кратности . Результаты занесены в таблицу (таб. 2).

 

Таблица 2

Ранжированные данные измерений по кости 299 d и их кратность

 

Данные измерений

Кратности

15

2

16

15

17

15

18

14

19

8

20

5

21

1

 

Методика проверки нормальности распределения данных

 

Подсчет теоретических кратностей при условии нормальности распределения по формуле

 

,

 

где n – число экспериментов, h=(b-a)/M – длина интервала разделения отрезка [a,b] на M равных величин.  В качестве отрезка [a,b] можно взять отрезок, на котором располагаются  экспериментальные данные.   Величина σ 2 служит оценкой дисперсии нормального закона распределения и рассчитывается по формуле

 

 ,

 

где   - срединное значение интервала разделения отрезка  [a,b], σ – среднеквадратичное отклонение,

 

 

есть оценка математического  ожидания нормального закона распределения.

Расчет величины

 

,

 

распределение которой при условии нормальности распределения экспериментальных данных совпадает с распределением случайной величины (СВ) ХИ-квадрат по  таблице распреления СВ ХИ-квадрат [9].

По заданному уровню ошибки α=0,05 и числу степеней свободы M-3 вычисляется квантиль ( и сравнивается с вычисленным значением  Если (, то расхождения между эмпирическими и расчетными кратностями согласно нормальному закону можно считать случайными и гипотеза о нормальности распределения принимается.

        

Проверка нормальности распределения данных для кости 299 d

 (из первого столбца данных таб. 1)

 

Проведены расчеты по приведенной методике для кости 299 d (из первого столбца таблицы 1).

Получено: ;

 

Таблица 3

Расчеты согласно приведенной методике для кости 299 d (из первого столбца таблицы 2)

 

Срединные значения интервалов

Кратности данных

Расчетные теоретические

кратности

Округленные расчетные кратности

15

1

1,693048

2

0,5

15,5

1

3,072448

3

1,333333

16

7

4,813322

5

0,8

16,5

8

6,632884

7

0,142857

17

7

8,040016

8

0,125

17,5

8

8,572518

9

0,111111

18

7

8,040016

8

0,125

18,5

7

6,632884

7

0

19

4

4,813322

5

0,2

19,5

4

3,072448

3

0,333333

20

3

1,725127

2

0,5

20,5

3

0,852029

1

4

21

1

0,370156

0

 

 

Отсюда = 8,17 (сумма величин последнего столбца).

Отрезок данных [15;21] разделен на интервалы с длиной h=0.5. В данном случае M=13 (число интервалов разделения).

Для α=0,05 и M - 3=10 найден по таблицам квантиль χ2 распределения (.

Так как (то гипотеза о нормальности распределения данных из первого столбца для выбранного уровня ошибки α=0,05 принимается.

Построен доверительный интервал для выбранного уровня ошибки α=0,05 по формуле

,

 

где где  , σ = 1,384, n = 60.  = (n/(n-1))σ =1,396.

В результате расчетов получен доверительный интервал, равный [17,139; 17,860]. Длина доверительного  интервала равна 0,72, что меньше единицы. Поэтому количество экспериментов n=60 вполне достаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинных трубчатых костей. При этом расчетная ошибка угла с выбранным уровнем ошибки будет не более полградуса.

Решение вопроса о достаточности 30 экспериментов для измерения угла скрученности для кости 299 d (первый столбец из таб. 1).

Были взяты первая и вторая выборки по 30 измерений для кости 299 d и проведены аналогичные расчеты (таб. 4)[3, 4, 5 , 6, 7, 8].

 

Таблица 4

Два блока результатов измерений кости 299 d из общего количества 60 (первые 30 измерений и вторые 30 измерений по таб. 1)

 

Первые 30 измерений

Вторые 30 измерений

21

18

20

18

20

19

18

18

17

17

18

19

18

20

18

16

16

16

16

17

16

17

17

16

16

17

15

19

19

17

16

18

16

19

16

18

17

17

17

20

18

18

16

17

15

19

18

16

17

17

18

16

19

18

16

17

17

16

19

20

 

Расчетные значения для первой группы из 30 данных представлены в таблице 5.

Таблица 5

Расчетные значения для первой группы из 30 данных

 

Срединные значения

отрезков

Кратности данных

Расчетные теоретические кратности

Округленные расчетные кратности

15,5

2

3,768794

4

1

16,5

9

6,86719

7

0,571429

17,5

6

7,978537

8

0,5

18,5

7

5,910645

6

0,166667

19,5

3

2,791991

3

0

20,5

3

0,840932

1

4

21,5

0

0,161501

0

 

 

Отсюда = 6,238. При расчете теоретических частот отрезок значений [15;21] был разбит на семь равных отрезков длиной 1, т.е. M=7, h=1. Квантиль χ2 распределения для уровня ошибки α = 0,05 с 4 степенями свободы (M-3=4)  равен 9,49, т.е. (. Так как (то гипотезу о нормальности распределения данных из первого столбца для выбранного уровня ошибки α=0,05 принимаем.

В результате расчетов получено:

, а доверительный интервал равен [16,768; 17,898].

Длина доверительного интервала равна 1,129, что больше единицы. Поэтому количество экспериментов n=30 недостаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинных трубчатых костей для первых 30 экспериментов.

Расчетные значения для второй группы из 30 данных представлены в таблице 6.

Таблица 6

Расчетные значения для второй группы 30 измерений для кости 299 d

 

Срединные значения отрезков

Кратности данных 

Расчетные теоретические кратности

Округленные расчетные кратности

16

6

3,929394

4

1

17

9

8,21775

8

0,125

18

7

9,114512

9

0,444444

19

5

5,430389

5

0

20

3

1,737983

2

0,5

 

Отсюда = 2,069444. При расчете теоретических частот отрезок  значений [16;20] был разбит на семь равных отрезков длины 1, т.е. M=5, h=1. Квантиль  χ2 распределения для уровня ошибки α=0,05 с 2 степенями свободы (M-3=2) равен 5,99, т.е. (. Так как (то гипотезу о нормальности распределения данных из первого столбца для выбранного уровня ошибки α=0,05 принимаем.

В результате расчетов получаем, что , а доверительный интервал равен [17,194; 18,139].  Видно, что длина доверительного интервала равна 0,944, что меньше единицы. Поэтому количество экспериментов  n=30 вполне достаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинных трубчатых костей для вторых 30 экспериментов. При этом  принятие 17,666 в качестве угла скрученности для первой кости будет не более полградуса с выбранным уровнем ошибки.

Как видно, полученные значения 17,666 и 17,333 мы расцениваем по-разному: первое принимаем, а второе отвергаем. Если округлять до целых значений градуса, то полагаем угол скрученности для первой кости, равной 18 градусов.

Если значения средних измерений углов скрученности  для кости 299 d (таб. 1) и длина доверительного интервала оказались не сильно отличающимися друг от друга в зависимости от выбора количества измерений (n=30, n=60), то для кости 92s все обстоит иначе. В данном случае значения средних и длина доверительного интервала зависят от выбора групп по 30 измерений (разница средних 0,86).

Были проведены все расчеты согласно приведенной методике для второго  столбца таблицы 1. Получили, что  ;  Данные измерений занесены в таблицу 7.

 

Таблица 7

Расчеты согласно приведенной методике по кости 92s

(из второго  столбца таблицы 1)

 

Срединные значения отрезков

Кратности данных 

Расчетные теоретические кратности

Округленные расчетные кратности

3

2

1,202463

1

1

3,5

2

2,130394

2

0

4

3

3,399471

3

0

4,5

4

4,88569

5

0,2

5

5

6,32417

6

0,166667

5,5

5

7,373001

7

0,571429

6

8

7,741911

8

0

6,5

8

7,321755

7

0,142857

7

7

6,236563

6

0,166667

7,5

7

4,784522

5

0,8

8

4

3,305939

3

0,333333

8,5

3

2,057379

2

0,5

9

1

1,153179

1

0

9,5

2

0,58216

1

1

10

0

0,264698

 

 

 

Отсюда = 4,880 (сумма величин последнего столбца). Здесь мы разбили отрезок данных [3;10] на интервалы с длиной h=0.5. В данном случае M=15 (число интервалов разделения). Для α=0,05 и M - 3=12 находим по таблицам квантиль χ2 распределения(. Так как (то гипотезу о нормальности распределения данных из первого столбца для выбранного уровня ошибки α=0,05 принимаем.

Теперь построим доверительный интервал для выбранного уровня ошибки α=0,05 по формуле

 

() ,

 

где  ; σ =1,532; = (n/(n-1)) σ= 1,545; n=60. Здесь 2,00 – значение, которое находится по таблице распределения Стьюдента с n-1=59 степенями свободы и уровнем ошибки α=0,05.

В результате расчетов получено: доверительный интервал равен [5,584; 6,382].  Длина доверительного  интервала равна 0,7982, что меньше единицы. Поэтому количество экспериментов n=60 вполне достаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинной трубчатой кости под номером 92s. При этом отклонение   от действительного значения  угла скрученности с выбранным уровнем ошибки α=0,05 будет не более полградуса.

Решение вопроса о достаточности 30 измерений угла скрученности для кости 92s для достоверной оценки действительного значения угла.

Вначале была рассмотрена первая группа из 30 измерений для кости 92s из таблицы 1. Расчетные значения для первой группы из 30 данных представлены в таблице 8.

 

Таблица 8

Расчетные значения для первой группы из 30 измерений по таблице 1

 

Срединные значения отрезков

Кратности данных

Расчетные теоретические кратности

Округленные расчетные кратности

3

1

0,762936

1

0

4

3

2,406866

2

0,5

5

3

5,109276

5

0,8

6

10

7,298107

7

1,28571429

7

5

7,014627

7

0,57142857

8

6

4,536724

5

0,2

9

2

1,974348

2

0,5

10

1

0,57816

1

0

 

Отсюда = 3,857 (сумма величин последнего столбца). Здесь мы разбили отрезок данных [3;10] на интервалы длиной  h=1.  В данном случае M=8 (число интервалов разделения). Для α=0,05 и M - 3=5 находим по таблицам квантиль χ2 распределения(. Так как   (то гипотезу о нормальности распределения данных из первого столбца для выбранногго уровня ошибки  α=0,05  принимаем.

Теперь построим доверительный интервал для выбранного уровня ошибки α=0,05 по формуле

 

( ),

 

где ; σ =1,562; = (n/(n-1)) σ= 1,588; n=30. Здесь 2,04 – значение, которое находится по таблице распределения Стьюдента с n-1=29 степенями свободы и уровнем ошибки α=0,05.

В результате расчетов получено, что доверительный интервал равен [5,808; 6,991]. Длина доверительного интервала равна 1,183, что больше единицы. Поэтому первых 30 экспериментов недостаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинной трубчатой кости под номером 2.

Для второй группы из 30 измерений для кости под номером 92s ситуация аналогично описанной выше. В этом случае ; σ =1,382;  = (n/(n-1)) σ= 1,406; n=30.

Теперь построим доверительный интервал для данной группы измерений для выбранного уровня ошибки α=0,05 (или уровня доверия 0,95) по формуле

( ).

 

Здесь 2,04 – значение, которое находится по таблице распределения Стьюдента с n-1=29 степенями свободы и уровнем ошибки α=0,05. В итоге получим следующий доверительный интервал [5,042; 6,090], длина которого 1,047, что больше единицы. Вывод: вторых 30 экспериментов  недостаточно для того, чтобы с уровнем ошибки α=0,05 принять  в качестве искомого угла скрученности длинной трубчатой кости под номером 92s.

Далее проведен анализ 60 экспериментальных данных для кости 67s из таблицы 1 (таб. 9).

 

Таблица 9

Анализ 60 экспериментальных данных для кости 67s

 

Срединные значения отрезков

Кратности данных 

Расчетные теоретические кратности

Округленные расчетные кратности

2

4

2,128726

2

2

2,5

4

3,15131

3

0,333333

3

4

4,303825

4

0

3,5

4

5,422634

5

0,2

4

7

6,303158

6

0,166667

4,5

7

6,759246

7

0

5

5

6,686988

7

0,571429

5,5

5

6,103164

6

0,166667

6

4

5,138919

5

0,2

6,5

4

3,991909

4

0

7

5

2,860762

3

1,333333

7,5

4

1,891364

2

2

8

3

1,153614

1

4

 

Отсюда = 10,971 (сумма величин последнего столбца). Здесь мы разбили отрезок данных [3;10] на интервалы с длиной  h=0.5.  В данном случае M=13 (число интервалов разделения). Для α=0,05 и M - 3=10 находим по таблицам квантиль χ2 распределения(. Так как   (то гипотезу о нормальности распределения данных из первого столбца для выбранного уровня ошибки α=0,05 принимаем.

Теперь построим доверительный интервал для выбранного уровня ошибки α=0,05 по формуле

( ),

 

где ; σ =1,746; = (n/(n-1)) σ= 1,761; n=60.

В результате расчетов получено, что  доверительный интервал равен [4,228; 5,138]. Длина доверительного интервала равна 0,909, что меньше единицы. Поэтому количество экспериментов n=60 вполне достаточно для того, чтобы с уровнем ошибки α=0,05 принять   в качестве искомого угла скрученности длинной трубчатой кости под номером 3. При этом отклонение   от действительного значения угла скрученности с выбранным уровнем ошибки α=0,05 будет не более полградуса.

Как показывают расчеты, доверительные интервалы с уровнем ошибки  α=0,05 для первой и второй кости объема выборки 30, и для третьей кости объема выборок 30, 40 и 50 имеют длину, большую единицы. Поэтому для выборок этих объемов среднее значение не гарантирует требуемую точность измерения углов с уровнем ошибки α=0,05.

Вывод на основании расчетов по 60 измерениям торсии для каждой из трех костей эксперимента. На основе проведенных 11 расчетов для трех различных костей (две выборки по 30 и 60 экспериментов для каждой из трех костей плюс выборки объемов по 40 и 50 для третьей кости) и рассмотрения наиболее неблагоприятных ситуаций можно утверждать, что наименьшее число экспериментов, для которого для всех трех типов костей длина доверительного интервала меньше единицы  с уровнем ошибки α=0,05 – это 60 экспериментов. Во всех трех случаях по результатам 60 экспериментов были построены доверительные интервалы, длины которых меньше единицы, что гарантирует точность измерения угла скрученности костей в полградуса.

Предложенный метод расчета углов скрученности костей быстрый, но обладает неточностью измерений (данные отличаются в 4 раза), что для достоверности расчетов может быть скомпенсировано большим числом экспериментальных данных.

У нас есть группы независимых данных, состоящие из 60 измерений угла скрученности для 60 костей, распределенные по нормальному закону, как мы это проверили для некоторых из них (таб. 10, 11, 12, 13, 14, 15). Если предположение о нормальности распределения данных справедлива для всех костей, то из независимости выборки костей должна следовать нормальность распределения средних для данных этих костей. Проверим данное предположение.

 

Таблица 10

Группа костей 1 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

299d

92s

67s

71d

97d

100d

60d

82d

95d

51d

68d

1

21

4

8

8

3

17

8

21

7

18

24

2

20

5

8

12

5

19

9

20

8

16

24

3

20

4

6

9

4

16

7

20

6

16

22

4

18

5

7

9

2

15

9

22

8

13

21

5

17

7

4

7

2

16

6

20

6

12

20

6

18

8

5

6

3

18

8

19

5

14

21

7

18

7

6

9

3

17

7

18

5

11

21

8

18

7

4

8

1

17

11

20

4

14

22

9

16

6

3

7

3

19

9

19

5

15

22

10

16

6

2

10

4

18

8

18

3

16

18

11

16

6

4

8

2

17

9

17

4

13

19

12

17

6

3

9

2

16

6

18

4

13

21

13

16

8

4

9

3

15

9

18

7

14

18

14

15

8

4

8

3

17

8

18

5

15

19

15

19

6

3

9

3

18

9

16

3

18

20

16

16

6

2

8

5

15

11

16

4

14

20

17

16

10

5

11

4

16

10

18

3

14

20

18

16

8

7

9

4

17

8

16

3

16

21

19

17

6

4

7

4

18

6

15

3

15

18

20

17

8

3

7

5

15

8

16

2

16

21

21

18

6

2

6

4

19

7

16

4

15

20

22

16

8

3

12

4

17

7

17

4

17

24

23

15

7

3

7

5

16

10

17

3

16

19

24

18

9

2

8

3

16

9

15

3

15

18

25

17

7

3

9

4

15

9

16

5

12

21

26

18

4

4

7

2

15

7

16

4

18

21

27

19

6

4

10

5

16

7

15

4

14

19

28

16

3

7

7

4

14

7

19

7

14

18

29

17

5

5

7

5

16

5

14

3

17

20

30

19

6

2

7

1

18

9

15

5

12

21

31

18

7

6

8

3

17

7

15

6

13

19

32

18

6

5

8

4

17

7

15

7

11

18

33

19

5

2

8

4

19

8

16

4

15

18

34

18

8

4

8

5

14

10

16

3

15

18

35

17

7

2

7

2

15

9

18

4

14

19

36

19

5

7

10

3

16

7

14

5

16

21

37

20

7

5

11

2

16

7

19

3

17

22

38

16

5

5

5

2

19

6

20

3

13

19

39

16

3

7

5

5

17

9

19

7

14

20

40

17

4

3

7

5

17

9

20

5

14

20

41

17

5

5

8

4

17

7

16

6

14

20

42

16

7

4

7

3

15

8

17

6

13

21

43

17

6

7

9

3

14

8

19

6

16

19

44

19

6

6

8

2

16

7

15

5

17

18

45

17

4

5

11

1

14

6

18

3

14

18

46

18

5

7

9

3

19

10

16

7

15

19

47

19

4

6

11

5

17

7

20

4

17

21

48

18

6

5

8

4

18

11

14

4

16

22

49

17

7

6

7

5

17

6

19

6

18

20

50

20

6

2

7

2

15

9

17

5

14

18

51

18

4

6

5

3

15

10

17

5

15

19

52

17

7

4

6

1

19

8

19

8

18

20

53

19

3

8

8

4

16

9

20

3

13

20

54

16

6

4

7

4

16

9

17

3

13

21

55

17

3

7

9

3

17

7

18

5

14

22

56

16

7

4

11

5

18

8

18

6

15

18

57

18

5

7

7

4

19

6

17

6

13

19

58

17

5

6

6

5

17

9

15

5

16

19

59

16

7

4

12

5

17

7

19

4

14

22

60

20

7

5

5

5

17

10

16

4

15

20

 

Таблица 11

Группа костей 2 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

57d

72d

81s

96s

80s

87s

93s

48s

63s

1

10

4

1

3

2

1

7

9

4

2

10

4

1

6

4

6

6

10

1

3

9

3

0

6

4

7

6

8

2

4

8

3

2

6

3

4

4

6

4

5

6

2

1

8

4

6

5

9

4

6

8

3

2

7

2

5

3

7

3

7

8

2

0

6

3

2

4

9

4

8

7

1

0

7

3

7

5

8

3

9

7

2

0

8

3

3

5

7

5

10

7

2

0

7

2

2

4

8

4

11

8

2

3

5

4

6

5

8

2

12

6

2

2

6

1

6

6

7

3

13

9

2

1

7

3

7

4

7

3

14

9

1

1

8

1

5

3

5

5

15

8

1

0

8

1

2

5

7

4

16

8

1

0

4

2

3

7

7

1

17

10

3

0

7

1

5

6

7

3

18

8

2

1

6

3

5

3

5

4

19

6

1

1

6

2

7

3

3

4

20

8

2

2

4

3

6

5

5

4

21

7

2

1

8

3

4

4

7

3

22

7

2

1

7

4

3

6

9

2

23

9

2

1

8

2

5

5

9

3

24

8

1

3

6

3

4

4

6

3

25

8

4

0

4

1

6

3

10

3

26

10

3

2

7

0

6

4

7

3

27

9

2

0

5

3

5

4

8

5

28

8

2

0

6

3

5

5

7

0

29

7

1

1

6

2

3

6

9

1

30

7

3

2

7

3

5

5

9

4

31

7

3

1

8

4

2

5

4

5

32

7

1

1

7

1

6

4

6

4

33

6

1

0

6

2

7

3

5

6

34

6

1

0

8

1

2

4

7

5

35

9

2

0

6

1

2

4

8

4

36

8

2

1

6

0

3

5

8

4

37

7

1

2

4

1

5

4

7

3

38

8

2

0

7

3

4

5

9

5

39

9

2

0

6

2

5

6

6

3

40

6

3

1

8

2

6

3

5

3

41

10

4

1

5

1

7

4

7

4

42

8

1

1

8

1

3

5

7

2

43

8

1

2

7

1

6

2

6

3

44

7

2

2

6

1

3

4

7

2

45

6

2

1

6

3

7

6

8

4

46

6

1

2

7

2

7

5

7

1

47

8

1

0

7

1

5

6

6

3

48

6

1

1

8

2

4

6

6

4

49

9

2

1

6

2

2

5

9

3

50

10

1

1

5

3

4

3

7

5

51

7

2

3

6

3

2

4

4

4

52

7

2

1

4

4

5

5

5

5

53

7

3

3

7

1

5

4

9

3

54

7

2

0

8

2

4

4

7

4

55

8

3

1

7

0

6

6

6

6

56

9

2

3

6

3

7

5

7

3

57

6

2

2

4

3

7

5

6

1

58

8

1

0

6

2

5

4

8

4

59

9

2

1

7

2

7

6

9

5

60

6

2

1

4

2

6

6

8

2

 

 

Таблица 12

Группа костей 3 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

46d

50d

13d

155d

148d

107d

106d

112d

122d

161d

1

5

4

0

6

8

-4

3

10

2

9

2

4

5

3

6

4

-1

1

11

3

10

3

7

5

-1

4

6

2

2

13

2

10

4

6

1

0

6

7

-1

1

12

1

8

5

8

6

-3

7

4

-4

0

13

-11

11

6

9

4

3

3

6

-5

-3

14

3

11

7

4

8

0

9

8

3

-2

13

1

12

8

4

3

-4

5

6

1

-3

12

2

13

9

5

4

1

5

3

-1

1

9

1

9

10

8

2

1

6

6

2

2

10

-1

11

11

7

5

4

7

5

0

0

15

-3

13

12

4

5

-1

5

4

-3

-2

11

0

12

13

8

6

2

6

5

-5

-2

12

0

11

14

9

7

-1

6

6

-4

0

13

0

9

15

8

4

3

4

9

-2

0

8

2

10

16

10

6

1

6

8

2

3

12

-1

11

17

6

5

1

6

3

3

1

13

-2

12

18

8

7

0

7

7

0

2

12

3

11

19

7

5

1

3

6

1

0

12

0

13

20

8

8

-1

2

5

-3

-2

13

2

11

21

8

4

-2

6

6

-5

-1

14

1

10

22

9

3

-3

5

7

-6

-1

13

-2

9

23

10

5

-3

4

8

-3

-2

14

3

9

24

4

5

-5

9

6

-1

4

15

-1

9

25

5

6

-1

9

6

0

2

12

0

10

26

4

7

3

5

7

-1

3

10

1

11

27

7

3

1

7

5

-3

0

9

3

12

28

6

5

-3

9

6

-3

1

10

2

11

29

6

2

-1

4

9

-4

0

14

1

12

30

9

6

0

6

4

-5

2

14

3

14

31

8

5

0

9

6

-3

2

15

1

11

32

9

5

-2

7

2

-5

2

12

4

10

33

10

7

4

6

3

-6

2

11

1

8

34

8

4

1

7

5

2

3

11

0

9

35

7

6

-1

8

4

0

2

13

-1

10

36

9

5

-1

9

6

-3

2

12

0

10

37

9

6

-2

9

7

2

1

11

-2

9

38

7

7

3

6

6

1

0

10

-1

10

39

4

4

5

7

5

0

-2

9

-3

9

40

9

8

-1

4

7

-2

-1

8

-1

14

41

8

3

0

3

6

-2

-2

9

0

12

42

10

6

2

6

1

-3

-2

13

1

13

43

9

5

-1

5

4

-5

-1

14

3

13

44

9

5

3

9

2

-3

-2

11

1

10

45

8

6

2

6

6

-5

-1

10

0

11

46

5

7

2

7

5

-5

-1

13

-1

10

47

9

4

3

8

4

-4

-3

15

1

11

48

6

7

3

9

7

-5

4

9

3

12

49

7

3

-2

5

5

0

1

11

1

11

50

9

6

-2

9

6

-1

1

14

2

14

51

8

5

-3

7

6

2

0

10

1

8

52

9

4

-1

9

5

1

0

10

2

11

53

6

7

-3

10

4

3

1

11

3

14

54

5

6

1

8

7

0

1

10

1

12

55

10

7

0

9

8

-5

1

12

2

10

56

7

7

1

7

7

-3

-1

13

0

11

57

9

8

0

9

8

-3

2

13

0

12

58

8

7

4

5

6

2

3

12

3

10

59

5

6

1

6

5

-4

1

12

1

12

60

9

7

1

9

7

1

3

11

-1

10

 

Таблица 13

Группа костей 4 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

195d

183d

189d

177d

242d

207d

209d

271d

272d

1

9

-8

16

8

10

7

3

9

20

2

6

-4

17

4

8

5

4

11

19

3

9

-7

19

7

13

7

1

10

18

4

9

-9

18

9

11

4

3

10

24

5

11

-10

16

7

14

9

0

11

21

6

12

-7

19

9

11

7

-1

9

24

7

10

-10

20

10

10

7

1

6

22

8

9

-11

22

6

9

4

2

9

23

9

8

-8

20

9

8

9

1

13

20

10

9

-9

20

7

11

10

-2

11

18

11

10

-7

17

8

13

11

0

9

22

12

9

-9

18

6

14

5

1

10

17

13

10

-10

19

10

13

4

3

11

23

14

11

-11

19

11

12

8

2

13

22

15

10

-9

17

7

11

11

4

11

21

16

11

-11

21

9

10

6

1

12

23

17

9

-6

22

9

10

9

0

11

24

18

12

-10

19

7

12

5

0

13

22

19

10

-11

19

8

13

7

2

14

23

20

9

-12

23

10

14

6

3

10

21

21

9

-9

21

4

14

8

1

9

20

22

10

-8

21

7

13

9

-2

8

20

23

9

-10

20

8

13

10

3

9

20

24

12

-9

19

6

15

7

5

10

23

25

13

-9

19

9

14

5

1

8

25

26

11

-11

18

10

13

6

3

9

21

27

10

-6

20

4

14

8

-1

11

22

28

9

-9

18

10

11

6

-2

13

21

29

14

-8

19

8

10

7

-1

13

18

30

11

-9

17

9

10

7

3

12

23

31

9

-10

19

9

9

8

3

14

19

32

10

-9

20

10

7

7

1

11

25

33

13

-7

22

9

12

6

2

12

23

34

11

-9

20

8

13

5

3

10

21

35

13

-12

19

7

13

9

0

11

22

36

9

-11

20

8

12

10

1

15

22

37

12

-11

21

7

11

8

2

12

19

38

10

-10

21

8

10

6

1

10

24

39

11

-9

22

9

13

5

1

11

23

40

13

-10

21

8

15

7

2

12

24

41

9

-12

19

9

10

6

1

13

21

42

7

-11

21

7

12

5

2

10

21

43

12

-11

22

10

11

7

4

9

22

44

9

-11

21

9

9

6

5

17

21

45

14

-9

19

7

10

8

0

10

21

46

10

-10

21

11

9

6

-3

9

22

47

6

-9

17

10

14

7

-1

8

23

48

10

-6

19

9

13

7

-2

9

23

49

9

-7

17

7

16

6

0

10

24

50

13

-9

25

9

13

5

1

9

21

51

11

-9

20

7

14

6

1

13

20

52

10

-10

19

8

11

7

-1

12

19

53

13

-9

19

9

10

8

-2

11

21

54

12

-8

21

10

11

9

-1

10

24

55

7

-10

17

11

9

11

-2

11

22

56

9

-11

21

11

12

8

3

9

22

57

10

-9

19

10

10

9

1

11

21

58

10

-9

21

11

10

7

2

11

20

59

9

-8

20

10

11

8

1

13

20

60

8

-7

21

9

14

6

0

12

21

 

Таблица 14

Группа костей 5 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

35s

1s

33s

8s

11s

37s

10s

6s

15s

12s

1

13

10

14

18

16

11

1

7

15

2

2

11

11

13

14

14

11

2

8

13

0

3

15

13

14

18

16

10

1

7

18

1

4

16

12

12

18

17

12

-2

7

16

1

5

12

11

16

16

17

10

0

4

17

3

6

10

10

16

15

14

13

-1

9

16

-2

7

14

8

14

20

19

12

1

9

18

1

8

16

11

12

14

15

13

3

5

15

3

9

15

7

10

17

18

14

1

6

19

3

10

17

11

12

16

13

11

-2

5

15

1

11

12

12

13

19

19

12

-3

9

15

0

12

14

13

15

16

16

10

1

7

18

0

13

11

11

15

19

17

9

3

8

17

-1

14

9

10

15

19

15

8

1

7

20

2

15

13

12

12

20

18

9

-1

9

16

-1

16

15

13

10

22

17

10

1

5

17

-3

17

12

13

11

19

19

11

1

7

18

-2

18

11

13

13

17

20

15

2

4

16

1

19

11

15

16

19

18

11

0

10

17

1

20

13

12

12

19

19

12

1

7

16

0

21

13

10

8

18

15

11

0

9

19

3

22

12

13

15

16

18

14

-1

7

18

1

23

14

11

13

17

16

14

-1

8

17

-2

24

15

14

15

18

15

15

-3

10

17

2

25

16

10

14

20

17

13

1

9

17

0

26

12

11

16

17

18

12

1

8

16

1

27

11

13

15

15

19

14

0

7

19

-3

28

13

15

13

18

16

11

2

9

15

2

29

12

12

17

19

18

10

3

6

16

4

30

12

11

12

20

20

7

1

9

17

1

31

11

9

13

22

21

10

2

8

19

2

32

12

10

12

19

19

8

1

7

14

0

33

13

12

12

18

15

11

2

4

19

1

34

12

10

12

17

18

13

1

11

17

-1

35

11

12

11

18

17

9

2

8

19

-1

36

14

11

13

19

19

10

0

9

20

2

37

15

13

12

19

17

11

-2

6

14

0

38

14

12

15

21

19

8

-3

8

17

-1

39

16

11

13

20

20

15

1

9

14

-1

40

10

13

16

16

17

12

-1

5

18

1

41

11

11

12

19

18

14

-2

10

19

2

42

16

14

11

18

16

12

-1

9

16

1

43

15

15

10

18

16

13

0

9

17

0

44

12

12

11

19

16

12

0

8

18

0

45

17

13

12

17

14

12

1

9

17

1

46

11

12

11

19

19

11

3

6

18

2

47

13

14

13

19

17

10

1

7

19

1

48

11

9

14

19

18

15

-2

5

16

-1

49

12

10

13

20

19

15

-2

9

20

2

50

16

17

15

15

16

14

1

8

16

1

51

13

14

12

16

17

14

3

10

16

3

52

15

13

12

18

19

13

0

7

18

1

53

12

12

11

17

16

14

-2

6

16

2

54

11

13

13

19

18

12

1

9

19

1

55

14

12

14

17

19

14

-1

7

15

0

56

15

11

13

21

17

15

0

9

19

2

57

14

13

13

20

19

12

4

6

17

3

58

12

12

12

19

17

15

-1

5

19

1

59

13

11

12

19

19

12

2

9

18

2

60

11

10

11

18

20

11

1

7

18

1

 

Таблица 15

Группа костей 6 (по 60 измерений предлагаемым способом)

 

№ кости

/

№ измер.

Угол скрученности в градусах

49s

60s

53s

148s

112s

126s

117s

140s

118s

249s

238s

1

14

10

-6

25

7

3

10

1

18

20

33

2

15

11

-5

22

7

2

11

4

20

17

35

3

13

11

-8

27

5

3

10

1

18

20

32

4

12

12

-4

26

6

2

11

2

19

19

35

5

14

13

-7

23

7

1

12

1

17

16

33

6

16

11

-8

27

5

2

11

0

20

19

31

7

15

12

-8

21

8

3

11

2

15

19

38

8

16

11

-9

24

4

0

11

4

18

18

33

9

17

10

-8

23

9

-1

12

1

19

19

35

10

13

9

-9

25

8

0

15

4

16

15

32

11

12

9

-10

26

7

3

10

6

18

19

32

12

19

10

-6

27

8

1

8

-1

19

14

31

13

17

13

-8

24

6

2

11

0

18

17

33

14

16

12

-5

23

8

4

14

3

17

16

32

15

17

11

-10

24

8

1

11

2

19

19

35

16

19

11

-6

23

9

-2

12

4

19

19

34

17

20

11

-9

25

7

0

15

-2

21

22

35

18

13

13

-11

21

8

2

10

0

18

18

31

19

16

12

-8

23

5

1

11

1

16

18

32

20

15

12

-9

24

6

0

12

-1

15

16

32

21

12

14

-9

23

4

3

12

3

19

19

35

22

15

17

-6

24

7

2

11

4

17

17

30

23

14

10

-7

23

4

1

12

1

18

19

32

24

18

12

-8

23

10

2

13

1

17

20

32

25

14

13

-7

22

7

1

11

0

15

15

34

26

12

14

-4

23

9

2

10

2

18

18

31

27

19

12

-8

24

6

2

7

1

19

16

30

28

16

11

-10

21

8

2

12

-2

18

18

29

29

15

10

-9

22

5

3

11

-2

16

18

31

30

17

12

-6

26

6

2

13

0

19

16

34

31

19

13

-5

23

7

1

14

0

20

17

32

32

18

12

-8

27

8

-1

11

1

16

17

33

33

15

11

-8

24

5

2

10

3

18

16

31

34

15

12

-7

23

7

1

10

1

16

19

35

35

21

14

-9

23

5

2

11

2

17

20

32

36

16

15

-7

25

6

2

16

1

14

18

33

37

17

14

8

21

8

1

12

3

17

19

32

38

18

12

-5

25

6

2

13

2

18

17

34

39

15

13

-8

27

8

0

12

3

17

17

31

40

16

10

-9

23

5

1

12

3

18

19

34

41

15

11

-10

24

7

1

11

2

17

17

31

42

17

12

-8

23

6

2

13

3

19

19

32

43

13

12

-7

25

8

4

14

1

20

20

35

44

14

13

-6

24

5

1

14

0

18

14

32

45

18

12

-9

23

8

2

13

1

19

17

31

46

18

11

-9

23

9

1

12

-1

15

16

34

47

15

12

-6

21

4

3

12

-1

18

18

33

48

14

15

-5

22

11

3

11

-2

17

16

33

49

17

12

-8

22

5

3

12

0

17

17

31

50

15

13

-9

25

6

4

15

0

19

18

35

51

15

13

-11

26

5

1

14

2

17

16

35

52

17

12

-9

27

7

0

11

1

18

19

32

53

16

12

-10

24

7

0

12

3

17

19

32

54

18

15

-8

27

7

-1

13

1

19

17

33

55

17

12

-7

27

8

0

10

4

16

18

34

56

17

10

-7

29

7

2

10

1

18

16

31

57

15

10

-7

23

7

3

16

1

16

17

30

58

16

14

-9

24

8

0

15

0

17

16

32

59

14

13

-11

25

9

-1

12

-1

16

19

31

60

14

14

-8

23

9

2

15

3

16

20

31

 

Средние для измерений всех 60 костей расположили в убывающем порядке (таб. 16).

 

Таблица 16

Средние измерений торсий для 60 случайно выбранных костей

в убывающем порядке

 

Средняя торсии

32,616667

24,033333

21,516667

20,05

19,616667

18,15

17,733333

17,6

17,5

17,4

17,35

17,083333

16,633333

15,333333

14,75

13,033333

12,95

11,703704

11,933333

11,866667

11,816667

11,8

11,633333

10,85

10,833333

10,166667

8,3833333

8,1333333

8,0666667

7,75

7,5333333

7,3166667

7,1166667

7,1166667

6,8666667

6,5166667

6,3166667

5,9833333

5,6666667

5,3166667

4,75

4,75

4,6833333

4,6666667

3,4666667

3,4

2,1833333

2

1,4666667

0,5477273

1,2833333

1,0333333

0,6

1,3392157

0,4333333

0,3666667

0,2

-1,71666

-8,25

-9,16666

 

Длина отрезка данных равна 42.

Выбрано разделение данных на интервалы длиной h согласно формуле

 

h = 42/(1+3.2 ln 60) = 2,98.

 

Округляем это значение до 3. Таким образом, разбиваем данные средних значений на группы по трем (таб. 17).

 

Таблица 17

Интервалы разделения и кратности попадания средних в них

 

Интервалы разделения данных

 

Экспериментальные кратности

 

-9

-6

2

-6

-3

0

-3

0

1

0

3

11

3

6

9

6

9

11

9

12

9

12

15

3

15

18

8

18

21

3

21

24

1

24

27

1

27

30

0

30

33

1

 

 

 

 

Вычислены теоретические кратности попадания в обозначенные отрезки нормально распределенных данных согласно приведенной ниже формуле

 

где n=60, h=3, xсеред, i - срединное значение для i-ого отрезка разбиения, xср – среднее значение для всей генеральной совокупности данных (таб. 18).

 

Таблица 18.

Теоретические кратности попадания в обозначенные отрезки

нормально распределенных данных

 

Интервалы разделения

 

Экспериментальные кратности

 

Средние значения интервалов

Теоретические кратности

 

-9

-6

2

-7,5

0,97

1

-6

-3

0

-4,5

2,06

2

-3

0

1

-1,5

3,76

4

0

3

11

1,5

5,9

6

3

6

9

4,5

7,94

8

6

9

11

7,5

9,19

9

9

12

9

10,5

9,13

9

12

15

3

13,5

7,79

8

15

18

8

16,5

5,71

6

18

21

3

19,5

3,59

4

21

24

1

22,5

1,94

2

24

27

1

25,5

0,9

1

27

30

0

28,5

0,36

0

30

33

1

31,5

0,12

0

 

Соседние отрезки объединены в большие, чтобы частоты попадания в них не были меньше 3. После объединения получены отрезки и кратности попадания средних в них (таб. 19)

 

Таблица 19

Результаты объединения соседних отрезков в большие

с частотой не меньше 3

 

Интервалы разделения

 

Экпериментальные кратности fi

 

Теоретические кратности f

 

Хи квадрат

(f-fi)2/f

 

-9

0

3

7

2,2857

0

3

11

6

4,1667

3

6

9

8

0,125

6

9

11

9

0,4444

9

12

9

9

0

12

15

3

8

3,125

15

18

8

6

0,6667

18

21

3

4

0,25

21

33

3

3

0

 

Сумма чисел последнего столбца равна χ2расч = 11,06. Всего девять интервалов разделения. По таблицам распределения χ2 определен квантиль для уровня ошибки α=0,05 с 6 степенями свободы (9-3=6) равен 12,6, т.е. χ2табл(α,6)=12,6. Так как χ2расч< χ2табл(α,6), то гипотезу о нормальности распределения средних для выбранного уровня ошибки α=0,05 принимается.

 

Выводы

 

Генеральная совокупность измеряемых 60 случайно выбранных костей распределена по нормальному закону. Возможно построение доверительных интервалов для средней генеральной совокупности.

Средняя для всех выборочных данных xср= 8,8922.

Выборочная дисперсия s2= 61,82.

Выборочное стандартное отклонение s= 7,89.

Все величины рассчитаны в статистическом пакете Excel 2010.

Доверительный интервал равен  где N =3600 – число экспериментов, 1,96 - квантиль распределения Стьюдента с уровнем доверия 0,95 и числом степеней свободы, большим 120 [9].

Доверительный интервал оказался равным (8,635; 9,1491), длина которого меньше единицы. Значит с уровнем доверия 0,95 можно утверждать, что средняя генеральной совокупности принадлежит интервалу (8,635; 9,1491) длина которого меньше единицы (один градус).

Т. о. показано, что для доверительного уровня 0,95 выбор 60-ти экспериментальных данных для каждой кости достаточен, чтобы длина доверительного интервала была меньше единицы независимо от выбора кости.

Статистическая обработка основывается на утверждении: что верно для случайной выборки, верно и для генеральной совокупности, из которой эта выборка получена. На основании этого принципа можно утверждать, что новый запатентованный способ измерения  угла скрученности для всей генеральной совокупности костей будет давать данные, средняя которых с уровнем доверия 0,95 принадлежит рассчитанному доверительному интервалу, длина которого меньше единицы (один градус).

 

литература

 

1.     Алексеев В. П. Остеометрия. Методика антропометрических исследований. – М.: Издательство «Наука», 1966. – 251 с.

2.     Меренков В. Г., Тейкина О. Ю. Способ измерения углов скрученности длинных трубчатых костей // Патент РФ № 2567828 C1. Бюл. № 31.

3.     Тейкина О. Ю., Меренков В. Г. Способ измерения угла скрученности бедренной кости // Удостоверение на рационализаторское предложение № 1580 от 29.01.2013 ; ГБОУ ВПО СГМУ Минздрава РФ.

4.     Гланц С. Медико-биологическая статистика / С. Гланц. – М.: Практика, 1999. – 334 с

5.     Гринхальх Т. Основы доказательной медицины / Т. Гринхальх. – М.: ГЭОТАР-МЕД, 2004. – 240с.

6.     Юнкеров В. И. Математико-статистическая обработка данных медицинских исследований / В.И. Юнкеров, С.Е. Григорьев. – СПб.: ВМедА, 2002. – 266 с.

7.     Платонов А. Е. Статистический анализ в медицине и биологии: задачи, терминология, логика, компъютерные методы / А.Е. Платонов. – М.: Издательство РАМН, 2001. – 52 с. 15.

8.     Пэтри А. Наглядная статистика в медицине / А. Пэтри, К. Сэбин. – М.: ГЭОТАР-МЕД, 2003. – 144 с. 16.

9.     Реброва О. Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA / О.Ю. Реброва. – МедиаСфера, 2002. – 70с.

10. Кремер Н. Ш., Путко Е. А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2002.- 311 с.

 

METROLOGICAL CHARACTERISTICS OF THE SIMPLE METHOD OF MEASURING THE ANGLE OF THE TORSION OF THE HUMAN HAIR TISSUE

 

© 2018 Teykina O. Yu., Merenkov V. G, Prudnikov I. M.

 

For the first time, a metrological evaluation of the original method of measuring the twist angle of a human thigh bone was carried out. The calculation of the mean, the construction of a confidence interval with a given level of significance, and an estimate of the number of experiments measuring the torsion angles of long tubular bones were performed.

Key words: femur, long tubular bone, epiphysis, diaphysis, torsion of bone, torsion transformation of bone, angle of twisted bone.

 

Кафедра анатомии человека

ФГБОУ ВО «Смоленский государственный медицинский университет»

Минздрава России

Россия, 214019, Смоленск, ул. Крупской 28.

Smolensk State Medical University,

28 – Krupskoi Street, Smolensk  214019, Russia.

Поступила в редакцию 21.05.2018