УДК 51
Лекция
ВЫЧИСЛИМОСТЬ. ВВЕДЕНИЕ В
ТЕОРИЮ АЛГОРИТМОВ
© 2000 г. Е. П.
Емельченков, В. Е. Емельченков
Рассматриваются основные понятия теории
алгоритмов. Исследуется неразрешимость многих
проблем важных для теоретического
программирования.
Понятие алгоритма является не только центральным понятием теории алгоритмов, не только одним из главных понятий математики вообще, но одним из главных понятий современной науки. Более того, сегодня, с наступлением эры информатики, алгоритмы становятся одним из важнейших факторов цивилизации.
Успенский В.А., Семенов А.Л. [1, c. 10]
Введение
Точное понятие "алгоритм" было выработано лишь в тридцатых годах XX века. До этого математики довольствовались интуитивным понятием алгоритма. Это объясняется тем, что до середины XIX века математика имела дело в основном с числами и вычислениями. Понятие алгоритма отождествлялось с понятием метода вычислений. Все многообразие вычислений комбинировалось из четко определенных операций арифметики, тригонометрии и анализа. Поэтому понятие метода вычисления считалось интуитивно ясным и не нуждалось в специальных исследованиях.
Новые более жесткие требования к строгости стимулировались в основном математикой нечисловых объектов во второй половине XIX века. Одним из решающих обстоятельств, приведших к пересмотру оснований математики, явилось создание Кантором теории множеств.
Опыт парадоксов теории множеств научил математику крайне осторожно обращаться с бесконечностью и даже о бесконечности рассуждать с помощью финитных методов. Существо финитного подхода заключается в том, что он допускает только конечные комплексы действий над конечным числом объектов. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и возможностями обладают комбинации элементарных действий, что можно и чего нельзя сделать с их помощью - все это стало предметом теории алгоритмов. Главным внутриматематическим приложением теории алгоритмов явились доказательства невозможности алгоритмического решения некоторых математических проблем. Такие доказательства неосуществимы без точного понятия алгоритма (для доказательства несуществования алгоритма решения того или иного класса задач, надо точно знать несуществование чего требуется доказать).
1. Интуитивное понятие алгоритма
Человек ежедневно встречается с множеством задач, возникающих в различных областях деятельности общества, например:
а) подготовиться к уроку по математике;
б) приготовить раствор для проявления фотопленки;
в) избавиться от лишнего веса.
Для решения задач надо знать, что дано, и что следует получить. Другими словами, задача представляет собой совокупность двух объектов: исходных данных и искомых результатов. Чтобы получить результаты, необходимо знать метод решения задачи, то есть располагать предписанием (инструкцией, правилом), в котором указано, какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить искомые результаты). Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, называется алгоритмом.
Алгоритм - это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата.
Следует иметь в виду, что это - не определение в математическом смысле слова, но довольно подробное описание понятия алгоритма, раскрывающее его сущность. Описание может быть другим. Так, в школьном учебнике по информатике [l] понятие алгоритма дается в следующей форме: "Под алгоритмом понимают понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи".
Понятие алгоритма является одним из основных понятий современной математики и является объектом исследования специального раздела математики - теории алгоритмов.
Еще на самых ранних ступенях развития математики в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам. К числу таких правил относились и правила выполнения арифметических операций над числами.
Столетия эти правила были очень сложны и не удивительно поэтому, что производить вычисления с большими числами могли только люди с высшим образованием. Так, чтобы научиться арифметическому делению в средние века требовалось закончить университет. Да еще не всякий университет мог научить этой премудрости. Нужно было непременно ехать в Италию: тамошние математики добились большого искусства в делении. Если напомнить, что в те времена пользовались непозиционной (римской) системой счисления, станет ясно, почему деление миллионных чисел было доступно лишь бородатым мужам, посвятившим этому всю свою жизнь.
С введением позиционной системы счисления все изменилось. В IX веке узбекский математик Мухаммед ибн Муса ал-Хорезми ("ал-Хорезми" означает "Хорезмиец") описал правила выполнения четырех арифметических действий в десятичной системе счисления. Новые правила были значительно проще и сейчас ими владеют уже школьники младших классов. Поразительная простота указанных правил стимулировала их повсеместное распространение. Эти правила были изложены Мухаммедом в книге по математике, изданной в 825 году, где, кроме того, приводились многочисленные рецепты решения различных задач.
По латинским переложениям арифметического трактата ал-Хорезми средневековая Европа знакомилась с индийской позиционной системой счисления и с искусством счета в этой системе. При переводе имя автора переделали в Алгоритми. Ссылки на рецепты решений из книги Мухаммеда европейские авторы начинали со слов: "Так говорил Алгоритми ...". С течением времени сами рецепты для решения математических задач стали называть алгоритмами.
Первоначально под алгоритмами понимали только правила выполнения четырех арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.
Для разъяснения интуитивного понятия алгоритма рассмотрим несколько примеров.
В качестве первого примера рассмотрим один из самых древних и самых известных математических алгоритмов - алгоритм нахождения наибольшего общего делителя двух натуральных чисел. Этот алгоритм еще в III веке до нашей эры изложил (в геометрической форме) греческий ученый Евклид в теоретическом трактате по математике "Начала". Поэтому он носит название алгоритма Евклида. Алгоритм Евклида обсуждается практически в каждой книге по программированию.
Пример 1.1. Вычисление наибольшего общего делителя двух натуральных чисел m и n.
Составим алгоритм решения этой задачи в предположении, что его исполнителем будет некоторое вычислительное устройство.
Алгоритм Евклида
1. Поместить в участок памяти с именем x число m; перейти к выполнению пункта 2.
2. Поместить в участок памяти с именем y число n; перейти к выполнению пункта 3.
З. Если выполняется условие , то перейти к выполнению пункта 5, иначе
перейти к выполнению пункта 4.
4. Поместить в участок памяти с именем НОД значение из блока памяти x; перейти к выполнению пункта 8.
5. Если выполняется условие x > y, то перейти к выполнению пункта 6, иначе перейти к выполнению пункта 7;
6. Поместить в участок памяти с именем x значение выражения x - y; перейти к выполнению пункта 3.
7. Поместить в участок памяти с именем y значение выражения y - x; перейти к выполнению пункта 3.
8. Закончить работу.
Внимательное рассмотрение алгоритма Евклида показывает, что запись алгоритма распадается на отдельные команды. Каждая команда снабжена номером и представляет собой указание исполнителю выполнить некоторое законченное действие. Исполнение алгоритма начинается с команды, имеющей номер 1. Далее команды выполняются в соответствии с указаниями, сопровождающими каждую команду алгоритма.
Для удобства ссылок, алгоритм обычно снабжается названием. В случае, когда для алгоритма не указывается специальное название, его названием обычно считают весь текст задачи, для решения которой этот алгоритм предназначен.
Существует правило, согласно которому, при отсутствии специального указания следующей за данной командой должна выполняться команда, номер которой на единицу больше данной. Такая последовательность выполнения команд называется естественной. По указанию "кончить работу" исполнение алгоритма прекращается.
Пример 1.2. Умножение натуральных чисел столбиком [2].
1. Записать множимое.
2. Подписать множитель под множимым так, чтобы разряды множителя находились под соответствующими разрядами множимого.
3. Провести черту под множителем (под ней будут записываться частные суммы).
4. Взять очередную цифру множителя, начиная с единиц.
5. Если очередная цифра множителя равна нулю, пропустить ее и перейти к пункту 7.
6. Если очередная цифра не равна нулю, умножить на нее множимое и произведение как очередную частную сумму, подписать под чертой или под предыдущей частной суммой так, чтобы единицы произведения находились бы под очередной цифрой множителя.
7. Если очередная цифра не была последней, перейти к пункту 4.
8. Если очередная цифра оказалась последней, сложить частные суммы столбиком и общую сумму взять в качестве искомого произведения.
Пример 1.3. Инструкция по приготовлению проявителя. Содержимое большого пакета растворить в 300 мл. воды при температуре I8-20° C; затем добавить содержимое малого пакета. Объем раствора довести до 500 мл. Раствор профильтровать.
В этом примере команды не пронумерованы. Все команды записаны последовательно, в виде сплошного текста. Друг от друга команды разделены либо точкой, либо точкой с запятой. При таком оформлении алгоритма исполнитель выполняет команды в порядке их естественного следования в тексте.
Такая форма записи алгоритма часто используется во всякого рода инструкциях, правилах, рецептах и т.п. Она хороша в случае, когда алгоритм небольшой и когда для описания алгоритма отводится мало места. Недостатком такого оформления является его малая наглядность .
Упражнения
1.1. Составьте алгоритм сложения столбиком двух натуральных чисел.
1.2. Опишите правила перехода улицы для случаев:
а) перекресток регулируемый;
б) перекресток нерегулируемый (т.е. без светофора).
1.3. Опишите способ измерения длинной рейки с помощью линейки.
1.4. Укажите метод отыскания слова в орфографическом словаре.
1.5. Укажите алгоритм проведения перпендикуляра к прямой l, в заданной точке D.
1.6. Опишите несколько алгоритмов решения задач на следующие темы:
а) рецепты приготовления пищи (один из способов получения таких рецептов - воспользуйтесь поваренной книгой);
б) правила этикета (например, правило знакомства, алгоритм приветствия и т.п.);
в) правила дорожного движения;
г) правила поведения в бытовых ситуациях (алгоритм пользования газовой плитой, правило пользования телефоном-автоматом и т.п.).
2. Свойства алгоритмов
Рассмотренные примеры показывают, что выполнение алгоритма разбивается на последовательность законченных действий-шагов. Каждое действие должно быть закончено исполнителем прежде, чем он приступит к исполнению следующего действия. Это свойство алгоритма называется дискретностью.
Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.
Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно, какую команду надо выполнить следующей. Это свойство алгоритма называется точностью.
Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может ее исполнить в строгом соответствии с ее назначением. Это свойство называется понятностью (для данного исполнителя).
- Да пойми же, гайками прикрепляется рельса к шпалам!
- Это мы понимаем...
А. Чехов "Злоумышленник"
Будучи понятным, алгоритм не должен все же содержать предписаний, смысл которых может восприниматься неоднозначно. Это означает, что одно и то же предписание после исполнения должно давать один и тот же результат.
В данном случае речь фактически идет о том, что запись алгоритма должна быть настолько четкой, настолько полной и продуманной в деталях, чтобы у исполнителя никогда не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места, для произвола исполнителя.
Отмеченное свойство называется свойством определенности, или детерминированности.
Замечание. Часто под свойством детерминированности алгоритма понимается одновременное выполнение свойств точности и понятности.
Важным свойством алгоритма является свойство результативности. Смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет.
Считается, что алгоритм наиболее интересен, если он, кроме того, обладает свойством массовости, т.е. пригодности для решения любой задачи из некоторого класса задач. Это свойство не следует понимать как возможность решить много задач. Свойство массовости предполагает, что заданный алгоритм позволяет решить любую задачу из определенного класса, причем этот класс может состоять и только из одной задачи.
Проиллюстрируем свойства алгоритма на примере алгоритма Евклида.
Массовость алгоритма Евклида заключается в
том, что его можно применить к любой паре
натуральных чисел. Результативность его состоит
в том, что он определяет процесс, приводящий для
любой пары натуральных чисел к получению их
наибольшего делителя. Понятность алгоритма
заключается в том, что исполнитель умеет
выполнять действия, определяемые командами
алгоритма. Детерминированность алгоритма
вытекает из того, что каждая команда выполняется
исполнителем однозначно. Точность алгоритма
обеспечивается тем, что, во-первых, исполнителю
известно, с чего начинать выполнение алгоритма (с
команды номер 1), и, во-вторых, каждая команда
снабжена указанием, какую команду выполнять
следующей.
Рис.2.1. Непонятное предписание
Очевидно, не каждое правило, приводящее к решению задачи, является алгоритмом. Разберем с этих позиций несколько таких правил.
Пример 2.1. Проведение перпендикуляра к прямой MN в заданной точке A [2].
I. Отложить в обе стороны от точки A на прямой MN циркулем отрезки равной длины с концами B и C,
2. Увеличить раствор циркуля до радиуса, в полтора-два раза большего длины отрезков AB в AC.
3. Провести указанным раствором циркуля последовательно с центрами B и C дуги окружностей так, чтобы они охватили точку A и образовали две точки пересечения друг с другом D и E.
4. Взять линейку и приложить ее к точкам D и E и соединить их отрезком. При правильном построении отрезок пройдет через точку А и будет искомым перпендикуляром
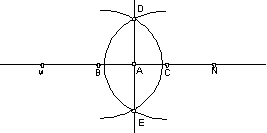
Рис. 2.2. Проведение перпендикуляра к
прямой в заданной точке
Указанное правило, очевидно, рассчитано на исполнителя-человека. Применяя его, человек, разумеется, построит искомый перпендикуляр. Но, тем не менее, это правило алгоритмом не является.
Прежде всего, оно не обладает свойством детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор отрезка произвольной длины (для построения точек B и C надо провести окружность произвольного радиуса r с центром в точке A). В пункте 2 требуется сделать выбор отрезка в полтора-два раза большего длины отрезков AB и AC. В пункте 3 надо провести дуги, которые также однозначно не определяются их описанием. Человек-исполнитель, применяющий данное правило, к одним и тем же исходным данным (прямой MN и точке A) повторно, получит несовпадающие промежуточные результаты. Это противоречит требованию детерминированности алгоритма.
Попробуем переформулировать это правило, чтобы оно стало алгоритмом. Для этого следует во всех предписаниях избавить исполнителя от проблемы выбора.
Для этого мы вместо выбора произвольного радиуса будем указывать в каждом случае конкретный. Однако, этим неопределенность команд полностью не снимается. В инструкциях 1 и 2, кроме проведения окружностей, требуется находить точки пересечения и как-то их обозначать. Разберем возникающие при этом проблемы.
В команде 2 требуется присвоить имена точкам
пересечения прямой MN и окружности . Здесь можно договориться
обозначать точки, например, так, чтобы векторы
и
были сонаправлены.
В команде 3 требуется обозначить точки
пересечения окружностей и
.
Договоримся, например, обозначать через D ту
из двух точек пересечения, которая находится
левее, если смотреть из центра B в направлении
центра C.
Кроме того, вместо дуг окружностей в пункте 3, мы будем проводить окружности, ибо тем самым снимается неопределенность инструкции "провести дугу, охватывающую точку".
С учетом сказанного искомый алгоритм может выглядеть следующим образом.
Пример 2.2. Алгоритм проведения перпендикуляра к
прямой MN в заданной точке A ().
1. Провести окружность
радиуса 1 с центром в точке A.
2. Обозначить точки пересечения окружности с прямой MN через B и
C так, чтобы
.
3. Последовательно провести окружности и
радиуса 2 с центром соответственно в
точках B и C.
4. Обозначить точки пересечения окружностей и
через D и E так, чтобы обход
многоугольника BDCE (последовательно от B
через D и C к E) совершался по часовой
стрелке.
5. Провести прямую DE. Прямая DE - искомый перпендикуляр.
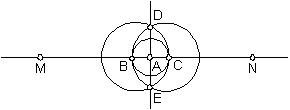
Рис.2.3. Проведение перпендикуляра к
прямой в заданной точке
В школьном учебнике [1] приведен алгоритм нахождения середины отрезка при помощи циркуля и линейки. В нем использован другой прием избавления от неопределенности инструкций при геометрических построениях.
Замечание. Подробное обсуждение вопросов,
связанных с алгоритмами построения циркулем и
линейкой, проводится в [3]. Всем, изучающим
информатику, полезно познакомиться с этой
интересной книгой.
3. Уточнение понятия алгоритма
"То, что вообще может быть сказано, может быть сказано ясно, а о чем невозможно говорить - о том следует молчать".
Людвиг Витгенштейн (Эпиграф, предпосланный изложению языка программирования АЛГОЛ-60.)
Точное математическое определение понятия "алгоритм" было выработано лишь в тридцатых годах XX века. Почему же до этого времени математики довольствовались интуитивным понятием алгоритма? Это связано с тем, что обычно понятие алгоритма встречалось в связи с конкретным решением задачи. Об алгоритме говорили лишь тогда, когда предлагался способ решения какого-либо класса задач. В начале XX века в математике накопилось большое количество задач, которые не поддавались решению, несмотря на то, что над ними думали первоклассные ученые. Возникло подозрение, что для некоторых из этих задач вообще не существует разрешающего алгоритма. Утверждение о неразрешимости того или иного класса задач можно было вывести, только имея точное определение алгоритма, надо было знать, несуществование чего требуется доказать.
Попытки дать строгое математическое определение алгоритма, согласующееся с интуитивным представлением об алгоритме, привели к выработке сразу нескольких определений (Черч, Пост, Тьюринг, Марков и др.). Впоследствии выяснилось, что все эти определения равносильны между собой и, следовательно, определяют одно и то же понятие.В качестве основы для уточнения понятия алгоритма мы выбираем так называемые машины с неограниченными регистрами, или, короче, МНР [4]. Изложение на базе МНР привлекательно ввиду близости этих машин к реальным ЭВМ.
Каждый алгоритм имеет дело с данными - входными, промежуточными и выходными. Поскольку мы собираемся уточнять понятие алгоритма, нужно уточнить и понятие данных. В качестве данных для МНР мы ограничиваемся множеством Z0 неотрицательных целых чисел. Такое ограничение не является существенным, поскольку другие виды объектов и операции над ними могут быть закодированы натуральными числами и представлены как операции над натуральными числами.
Ниже мы перечислим все команды из списка предписаний МНР (для уточнения свойства "понятность"), однозначно определим действие каждой команды (для уточнения свойства "определенность") и опишем механизм реализации алгоритма (для уточнения свойства "точность").
Машина с неограниченными регистрами
является исполнителем, представляющим собой
простой "идеализированный компьютер".
Идеализация состоит в том, что каждый отдельный
реальный компьютер ограничен как величиной
чисел, которые поступают на вход, так и размером
памяти (необходимой для запоминания
промежуточных результатов), МНР лишена этих
ограничений. Машина с неограниченными
регистрами имеет неограниченно большую память,
ячейки которой будем называть регистрами и
обозначать Каждый
регистр в любой момент времени содержит
неотрицательное целое число.
|
... |
|||
|
... |
Рис. 3.1. Регистры МНР
При этом только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры заполнены нулями. Это допущение предполагает, что каждый алгоритм использует только конечный объем памяти.
В список предписаний МНР входит четыре команды:
команда обнуления Z(n); команда прибавления
единицы S(n); команда переадресации T(m, n) и
команда условного переходам J(m, n, q). Команды
обнуления, прибавления единицы и переадресации
называются арифметическими.
Обозначение |
Действие, производимое МНР |
Z(n) |
|
S(n) |
|
T(m, n) |
|
J(m, n, q) |
Если |
Рис. 3.2. Список предписаний МНР
Алгоритмом называется конечная непустая последовательность команд из списка предписаний МНР, начинающаяся с команды с номером 1.
Производя вычисления по данному алгоритму, МНР
изменяет содержимое регистров памяти в точном
соответствии с командами алгоритма. Исходное
состояние памяти, то есть последовательность
чисел в регистрах
перед началом
вычислений, называется начальной
конфигурацией.
Предположим, что некоторый алгоритм P состоит из последовательности команд I1, I2, ..., Is. МНР начинает вычисление с команды I1, затем выполняются команды I2, I3 и т. д. до тех пор, пока не встретится команда вида J(m, n, q). В этом случае МНР переходит к выполнению команды, предписанной J(m, n, q) и текущим содержанием регистров Rm и Rn
Пример 3.2. Рассмотрим алгоритм P1
I1 |
J(1, 2, 6) |
I2 |
S(2) |
I3 |
S(3) |
I4 |
J(1, 2, 6) |
I5 |
J(1, 1, 2) |
I6 |
T(3, 1) |
Применим алгоритм к следующей начальной
конфигурации:
R1 |
R2 |
R3 |
R4 |
R5 |
... |
5 |
3 |
0 |
0 |
0 |
... |
Рис. 3.3. Начальная конфигурация
Ход вычисления на МНР по алгоритму P1 с
начальной конфигурацией, изображенной на
рисунке 3.3, можно представить, записывая
последовательно сверху вниз конфигурации машины
вместе со следующей командой, к которой она
переходит на данном шаге.
R1 |
R2 |
R3 |
R4 |
R5 |
... |
Следующая команда |
||
5 |
3 |
0 |
0 |
0 |
... |
I1 |
||
5 |
3 |
0 |
0 |
0 |
... |
I2 |
(так как R1 R2) |
|
5 |
4 |
0 |
0 |
0 |
... |
I3 |
||
5 |
4 |
1 |
0 |
0 |
... |
I4 |
||
5 |
4 |
1 |
0 |
0 |
... |
I5 |
(так как R1 R2) |
|
5 |
4 |
1 |
0 |
0 |
... |
I2 |
(так как R1 = R2) |
|
5 |
5 |
1 |
0 |
0 |
... |
I3 |
||
5 |
5 |
2 |
0 |
0 |
... |
I4 |
||
5 |
5 |
2 |
0 |
0 |
... |
I6 |
(так как R1 = R2) |
|
2 |
5 |
2 |
0 |
0 |
... |
I7 |
||
Рис. 3.4. Вычисление по алгоритму P1
МНР выполняет алгоритм P: I1, I2, ..., Is до тех пор, пока это возможно. Вычисление останавливается тогда и только тогда, когда нет следующей команды, то есть когда МНР только что выполнила команду Ik и следующая команда в вычислении есть Iv, где v > s. Это может произойти одним из способов:
I) если Ik = Is (выполнена последняя команда в P) и Ik - арифметическая команда;
2) если Ik = J(m, n, q), Rm = Rn и q > s.
3) если Ik = J(m, n, q), Rm Rn и q = s.
В этом случае будем говорить, что вычисление остановилось после выполнения команды Ik, и заключительная конфигурации есть последовательность r1, r2, r3, ... содержимого регистров на этом шаге.
Результатом применения алгоритма к некоторой начальной конфигурации будем считать число r1 из регистра R1 заключительной конфигурации.
Бывают, конечно, вычисления, которые никогда не
заканчиваются, например, никогда не
заканчивается ни при какой начальной
конфигурации вычисление по алгоритму:
I1 |
S(1) |
I2 |
J(1, 1, 1) |
В случае, если вычислительный процесс не
заканчивается получением результата, говорят,
что алгоритм неприменим к начальной
конфигурации.
Упражнение
Для удобства обозначим через P(a1, a2, ..., an) вычисление по алгоритму P с начальной конфигурацией
a1, a2, ..., an, 0, 0, .... Если вычислительный процесс заканчивается с результатом b, будем писать
P(a1, a2, ..., an) = b.
Определение 3.1. Пусть f - функция от n неотрицательных
целых переменных со значениями во множестве Z0
неотрицательных целых чисел (функция ). Функция f называется
вычислимой на МНР (или МНР-вычислимой),
если существует такой алгоритм P, что
1) вычисление P(a1, a2, ..., an) останавливается тогда и только тогда, когда (a1, a2, ..., an) принадлежит области определения f;
2) если (a1, a2, ..., an) принадлежит области определения f; то в заключительной конфигурации в регистре R1 находится целое число b такое, что f(a1, a2, ..., an) = b.
С этого момента под термином вычислимое будем подразумевать МНР-вычислимое.
Рассмотрим теперь несколько простых примеров вычислимых функций.
Пример 3.2. Докажите МНР-вычислимость функции x + y.
Решение. Получим x + y, прибавляя y
раз 1 к числу x. Начальной конфигурацией
алгоритма служит x, y, 0, 0, 0, .... Типичной
конфигурацией в процессе вычисления является
R1 |
R2 |
R3 |
R4 |
R5 |
... |
x + k |
y |
k |
0 |
0 |
... |
Определим алгоритм следующим образом:
I1 |
J(3, 2, 5) |
I2 |
S(1) |
I3 |
S(3) |
I4 |
J(1, 1, 1) |
Заданный алгоритм вычисляет функцию x + y.
Пример 3.3. Докажите МНР-вычислимость функции
Решение. Составим алгоритм для начальной
конфигурации x, 0, 0, ... . Типичной
конфигурацией в процессе вычисления является:
R1 |
R2 |
R3 |
R4 |
R5 |
... |
x |
k |
k + 1 |
0 |
0 |
... |
Следующий алгоритм МНР-вычисляет функцию.
I1 |
J(1, 2, 6) |
I2 |
S(2) |
I3 |
J(1, 2, 6) |
I4 |
S(3) |
I5 |
J(1, 1, 2) |
I6 |
T(3, 1) |
Упражнения
3.2. Составьте алгоритмы, вычисляющие функции:
а) 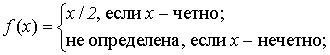
б) 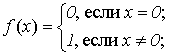
в)
г) 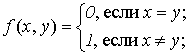
д)*
е)* 
Здесь [x / y] означает наименьшее целое число, не превосходящее действительное число x / y.
3.3. Покажите, что для каждой команды переадресации существует программа без команд переадресации, которая на всякой конфигурации МНР дает тот же результат, что и T(m, n). Это означает, что команды переадресации на самом деле избыточны в нашем определении МНР. Тем не менее, представляется естественным и удобным иметь такие команды, облегчающие построение алгоритмов.
Введем еще несколько понятий необходимых для дальнейшего изложения.
Определение 3.2. n-местным предикатом на множестве M называется отображение H, сопоставляющее каждому упорядоченному набору (a1, a2, ..., an) элементов из M одно из логических значений "истинно" или "ложно".
Пример 3.4. Функции "быть простым числом", "быть четным числом" являются одноместными предикатами на множестве целых чисел.
Пример 3.5. Свойства "иметь одинаковые остатки при делении на 3" или "быть равными" являются бинарными предикатами на множестве целых чисел.
Определение 3.3. Предикат называется разрешимым, если его характеристическая
функция
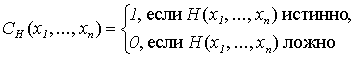
вычислима.
В контексте вычислимости предикаты часто называют проблемами. Поэтому ниже мы наряду с термином "разрешимый предикат" будем использовать также "разрешимая проблема".
Упражнение
3.4. Докажите разрешимость следующих предикатов на множестве целых неотрицательных чисел:
а) x = y;
б) ;
в) x < y;
г) x - четное число.
За последние пятьдесят лет было предложено много математических уточнений интуитивного понятия "алгоритм". Подход, основанный на МНР, является одним из них. Между этими подходами имеются большие различия, и в то же время все эти подходы эквивалентны между собой в том же смысле, что каждое уточнение алгоритма приводит к одному и тому же классу вычислимых функций.
Возникает теперь вопрос: насколько хорошо неформальное интуитивное понятие вычислимой функции отражено в различных формальных описаниях? Этот вопрос подвергался математиками серьезному обсуждению, в результате которого было высказано утверждение, известное под названием "тезис Черча": каждая функция, вычислимая посредством процесса, алгоритмический характер которого интуитивно ясен, является вычислимой функцией. Применительно к нашему изложению этот тезис можно перефразировать следующим образом: всякая функция, для которой существует алгоритм (в интуитивном смысле) вычисления ее значений, является МНР-вычислимой функцией.
Сразу же заметим, что это утверждение не является теоремой, подлежащей математическому доказательству; оно имеет статус утверждения, принимаемого как постулат, справедливость которого подтверждается рядом свидетельств. Во-первых, таким свидетельством является то, что, как уже отмечалось, многие независимые уточнения интуитивного понятия вычислимой функции привели к одному и тому же классу функций. Во-вторых, никому не доводилось найти функцию, которую можно признать вычислимой в интуитивном смысле и которая не была бы МНР-вычислимой. Исходя из этих соображений и собственного опыта, большинство математиков приняли тезис Черча.
4. Нумерация программ для МНР
Определение 4.1. Множество X называют счетным,
если можно установить взаимно однозначное
отображение между
множеством неотрицательных целых чисел Z0
и множеством X.
Определение 4.2. Множество называют не более чем счетным, если оно счетно или конечно.
Определение 4.3. Перечислением или нумерацией
множества X называется отображение множества Z0
на множество X.
Перечисление f определяет на множестве X
некоторую бесконечную последовательность элементов из X такую,
что каждый из элементов множества X
встречается в этой последовательности, по
крайней мере, один раз.
Если отображение f - взаимно однозначно, то f называют перечислением или нумерацией без повторений.
Определение 4.4. Множество X называется
эффективно счетным, если существует функция , устанавливающая взаимно
однозначное соответствие между множествами Z0
и X такая, что f и f--1 - вычислимые
функции.
Теорема 4.1. Следующие множества являются эффективно счетными:
а) ;
б) ;
в) - множество всех
конечных последовательностей целых
неотрицательных чисел.
Доказательство. а) Докажем сначала эффективную
счетность множества ,
состоящего из упорядоченных пар (x, y) с
целочисленными неотрицательными компонентами x
и y. Геометрически это множество
представляет целочисленную решетку (рис. 4.1).
Рис. 4.1. Целочисленная решетка
Перенумеровать точки этой решетки можно
различными способами, например, так, как показано
на рисунке 4.2.
Рис. 4.2. Нумерация точек целочисленной
решетки
Предложенная нумерация устанавливает взаимно
однозначное отображение между множествами
и
.
Алгоритмический характер процесса вычисления
значений функции
очевиден. Следовательно, по тезису Черча
- вычислимая функция.
Для вычисления значений обратной функции можно, например, в
соответствии с предложенным алгоритмом
последовательно нумеровать точки целочисленной
решетки до номера z. Пара (x, y) координат
точки с номером z является значением обратной
функции
. По тезису
Черча
- вычислимая
функция.
Таким образом, множество эффективно счетно.
б) Теперь несложно доказать эффективную
счетность множества .
Для этого определим взаимно однозначное
отображение
множества
упорядоченных троек
неотрицательных целых чисел на множество
следующим образом
. Из вычислимости функций
и
вытекает вычислимость функций
и
. Поэтому множество
эффективно счетно.
в) Для доказательства эффективной счетности
множества всех конечных последовательностей
целых неотрицательных чисел рассмотрим функцию
,
сопоставляющую каждому упорядоченному набору (a1, a2, ..., ak) из k неотрицательных целых чисел некоторое неотрицательное целое число.
Для доказательства взаимной однозначности
функции используем тот
факт, что у каждого целого числа имеется ровно
одно представление в двоичной системе счисления.
Запишем значение функции
в двоичной системе счисления:
(*)
Например,
=
= = 616 - 1 = 615;
=
= 2320 -1 = 2319;
= 544 -1 = 543;
= 520 - 1 = 519;
= 3 - 1 = 2;
= 32 - 1 = 31;
= 1 - 1 = 0.
Однозначность отображения следует из того, что
.
Так как, кроме того, для любого
неотрицательного числа x существует,
очевидно, кортеж (c1, c2, ..., cn) такой, что , то функция
устанавливает взаимно однозначное
соответствие между множеством
и множеством
.
Покажем, как вычисляются значения обратной
функции для
произвольного неотрицательного числа x.
В соответствии с формулой (*)
,
где - запись числа x + 1
в двоичной системе счисления.
Например,
;
;
;
;
;
;
;
.
В силу тезиса Черча функции и
вычислимы.
Следовательно,
-
эффективно вычислимое множество.
Теорема 4.2. Множество K команд МНР эффективно счетно.
Доказательство. Множество K команд МНР
включает четыре типа команд Z(n), S(n), T(m, n), J(m, n, q), где
. Определим взаимно
однозначное отображение
следующим образом:
= 4 (n - 1);
= 4 (n - 1) + 1;
;
,
где - отображения,
определенные в теореме 4.1.
Так как функции ,
очевидно, вычислимы, то отсюда вытекает
эффективная счетность множества K команд
МНР.
Теорема 4.3. Множество P всех программ для МНР эффективно счетно.
Доказательство. Пусть - произвольная программа для МНР.
Определим взаимно однозначное отображение
следующим образом:
.
где - отображения,
определенные в теореме 4.1. Так как функции
, очевидно, вычислимы, то
отсюда вытекает эффективная счетность множества
P всех программ для МНР.
Разумеется, существует много других
отображений из P в , устанавливающих эффективную счетность
множества P. Для нашего изложения
подходит любое из таких отображений. Зафиксируем
одно из них, например, то которое описано в
теореме 4.3.
Определение 4.5. Число (P) называется геделевым номером программы P или просто номером программы P.
Отображение играет важную роль в теории алгоритмов. Название числа (P) связано с именем К. Геделя, впервые в 1931 году предложившего идею кодирования нечисловых объектов натуральными числами.
Ниже программу P с геделевым номером n
будем обозначать . Из
взаимной однозначности отображения следует
при
, хотя обе эти программы
и
могут
вычислять одну и ту же функцию.
Пример 4.1. Найдем геделев номер программы P:
,
,
вычисляющей функцию f(x) = x + 2.
.
(S(1)) = 4 (1 - 1) + 1 = 1;
.
Пример 4.2. Вычислим программу по ее геделеву номеру m.
1) m = 0.
;
.
Следовательно,
: 1. Z(1).
2) m = 1.
;
.
Следовательно,
: 1. S(1).
3) m = 2.
;
.
Следовательно,
: 1. Z(1),
2. Z(1).
4) m = 3.
;
.
Следовательно,
: 1. T(1, 1).
Заметим, что различные программы и
вычисляют одну и ту же функцию f(x) = 0.
5. Нумерация вычислимых функций
Определение 5.1. Пусть f - n-местная
функция, вычислимая по программе P с
геделевым номером m = (P). Число m
будем называть индексом функции f.
Вычислимую функцию от n переменных с индексом
m будем обозначать символом .
Из определения 5.1 следует, что каждая n-местная
вычислимая функция f представлена в
перечислении
Ниже мы в основном будем рассматривать
одноместные вычислимые функции . Для простоты в их обозначении
верхний индекс будем опускать.
Упражнение
5.1. Докажите, что у каждой вычислимой функции имеется бесконечно много индексов.
Приступим теперь к доказательству теоремы о существовании невычислимых функций. Идея доказательства этой теоремы столь же важна, как и результат.
Теорема 5.1. Существует невычислимая всюду определенная функция.
Доказательство. Пусть
- некоторое перечисление всех вычислимых
функций:
Положим
Функция g отличается от любой вычислимой
функции в точке n.
Действительно, если функция
определена в точке n, то
. Если
не
определена в точке n, то g отличается от
тем, что значение g(n)
определено. Таким образом,
и, следовательно, g - невычислимая
всюду определенная функция.
Метод построения функции в теореме 5.1 является примером диагональной конструкции, открытой Кантором. Лежащая в его основе идея является центральной в доказательстве большинства результатов, связанных с вычислимостью функций, и применима к огромному числу ситуаций, возникающих в различных разделах математики.
Поясним, почему для примененного в теореме 5.1
метода выбран термин диагональный. Для этого
проиллюстрируем метод построения функции g с
помощью следующей бесконечной таблицы:
0 |
1 |
2 |
3 |
... |
|
|
... |
||||
|
... |
||||
|
... |
||||
|
... |
||||
... |
... |
... |
... |
... |
... |
Рис. 5.1. Диагональная конструкция
При построении функции g для определения
значений в точках n выбирались диагональные
элементы таблицы .
Выбранные значения изменялись так, чтобы
обеспечить отличие g(n) от
.
Очевидно, что новые значения функции можно
выбирать сравнительно свободно. Например,
функция
является другой невычислимой всюду определенной функцией.
Проиллюстрируем диагональную конструкцию на примере из теории множеств.
Пример 5.1. Докажем, что множество всех
подмножеств множества
нельзя перечислить (перенумеровать).
От противного, пусть
- перечисление всех подмножеств множества
. Определим новое
подмножество B множества
следующим образом:
.
Очевидно, , что
противоречит предположению. Поэтому множество
всех подмножеств множества
нельзя перечислить.
Из доказанного вытекает, что множество всех
подмножеств множества
несчетно.
Упражнения
5.2. Используя диагональный метод, докажите что множество всех функций из N в N несчетно (Кантор).
5.3. Докажите, что множество всех невычислимых всюду определенных функций из N в N несчетно.
6. Универсальные программы
В этом разделе мы докажем несколько неожиданный результат, состоящий в том, что существуют универсальные программы, то есть программы, которые в некотором смысле реализуют все другие программы. Этот результат является одним из основных результатов теории вычислимости.
Определение 6.1. Универсальной функцией для n-местных
вычислимых функций называется (n+1)-местная
функция
.
Для примера рассмотрим функцию . Эта функция реализует все
одноместные вычислимые функции
. Действительно, для произвольного
неотрицательного целого числа т функция
совпадает с функцией
. Таким образом, название
функции
вполне
соответствует классу вычисляемых ею одноместных
функций.
Ниже для простоты вместо будем писать
.
Теорема 6.1. Для каждого натурального числа n
универсальная функция
вычислима.
Доказательство. Покажем, как можно
вычислить значение функции для заданного числа m и фиксированного
набора (x1, ..., xn). Неформальная
процедура вычисления значения
состоит в следующем:
"Декодируйте число m и восстановите
программу Рm. Затем имитируйте
вычисление по этой программе. Если вычисление по
программе заканчивается, требуемое значение
содержится в регистре R1".
По тезису Черча заключаем, что функция
вычислима.
Определение 6.2. Любая программа Р(n),
вычисляющая функцию ,
называется универсальной программой.
Универсальные программы полностью соответствуют своему названию. Действительно, так как универсальная программа Р(n) позволяет вычислить любую n-местную вычислимую функцию, то, по сути дела, программа Р(n) заменяет абсолютно все программы для вычисления n-местных функций.
Проиллюстрируем теперь, как использовать
вычислимость универсальных функций в
диагональных построениях.
7. Алгоритмически неразрешимые проблемы
Основным стимулом, приведшим к выработке понятия алгоритма и созданию теории алгоритмов, явилась потребность доказательства неразрешимости многих проблем, возникших в различных областях математики. Специалист, решая задачу, всегда должен считаться с возможностью того, что она может оказаться неразрешимой.
При доказательстве неразрешимости той или иной проблемы часто используется так называемый метод сводимости, заключающийся в следующем. Пусть, например, в результате некоторых рассуждений удалось показать, что решение проблемы Pr1 приводит к решению другой проблемы Pr2. В этом случае говорят, что проблема Pr2 сводится к проблеме Pr1. Таким образом, если проблема Pr2 сводится к проблеме Pr1, то из разрешимости Pr1 следует разрешимость Pr2 и, наоборот, из неразрешимости Pr2 следует неразрешимость Pr1. В данном разделе метод сводимости используется при доказательстве теоремы 7.3.
Ниже доказывается неразрешимость ряда известных проблем.
Теорема 7.1. Проблема "функция всюду определена" неразрешима.
Доказательство. Пусть g - характеристическая функция этой проблемы
Нам надо показать, что функция g невычислима.
От противного, предположим, что g - вычислимая функция. Рассмотрим функцию
Функция f всюду определена и отличается от
каждой вычислимой функции .
Применяя g и универсальную функцию , запишем f в виде:
Из вычислимости функций g и по тезису Черча следует
вычислимость функции f.
Полученное противоречие доказывает
невычислимость функции g. Таким образом,
проблема "функция
всюду определена" неразрешима.
Обозначим область определения и множество значений
функции
через
и
соответственно.
Теорема 7.2. Проблема "" неразрешима.
Доказательство. Характеристическая функция этой проблемы задается следующим образом:
Предположим, что функция g вычислима, и приведем это предположение к противоречию.
Рассмотрим функцию
Так как функция g вычислима, то по тезису
Черча функция f также вычислима. С другой
стороны, для любого x область определения Dom(f)
функции f отлична от области определения , и, следовательно,
.
Таким образом, предположение о вычислимости
характеристической функции g неверно.
Поэтому проблема ""
неразрешима.
Замечание 7.1. Доказанная теорема вовсе не
утверждает, что мы не можем для любого
конкретного числа a сказать, будет ли
определено значение . В
теореме лишь утверждается, что не существует
единого общего метода решения вопроса о том,
будет ли значение
определено.
Замечание 7.2. Проблему "" называют также проблемой
самоприменимости. Такое название связано с
формулировкой проблемы в форме: "Остановится
ли МНР, работая по программе
с начальной конфигурацией (x)?".
Другими словами: "Применима ли программа к
своему кодовому номеру?".
Теорема 7.3. Проблема "" неразрешима.
Доказательство. Если бы проблема "" была разрешима, то
была бы разрешима более простая проблема "
", что противоречит
доказанной выше теореме.
Замечание 7.3. Доказанную теорему часто интерпретируют как утверждение о неразрешимости проблемы остановки, в которой говорится, что не существует общего метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не существует общего метода проверки программ на наличие в них бесконечных циклов.
В доказательстве теоремы мы показали, что
проблема остановки "",
по крайней мере, не проще, чем проблема
самоприменимости "
".
Мы свели вопрос о неразрешимости одной проблемы
к другой. Это прием часто используется при
доказательстве неразрешимости проблем.
8. s-m-n-теорема
В этом разделе мы докажем теорему, принадлежащую к числу основных результатов теории алгоритмов. Суть теоремы в следующем. Допустим, что f(х, у) - вычислимая функция. Для каждого фиксированного значения a переменной х функция f порождает одноместную вычислимую функцию ga(y) = f(a, у). Из вычислимости функции ga следует существование индекса b такого, что f(a, у) = fb(у). Оказывается индекс b можно эффективно вычислить по параметру а.
Теорема 8.1 (s-m-n-теорема, простая форма). Пусть f(х, у) -вычислимая функция. Существует всюду определенная вычислимая функция s(x), такая, что f(х, у) = fs(x)(у).
Доказательство. Из вычислимости функции f(х, у)
следует существование МНР-программы Pr,
которая, исходя из начальной конфигурации (x, y, 0,
0, ...), вычисляет значение функции f от двух
аргументов х и у. Изменим программу Pr,
добавив спереди команды, преобразующие
начальную конфигурацию
R1 |
R2 |
R3 |
R4 |
... |
||
y |
0 |
0 |
0 |
... |
(*) |
в конфигурацию
R1 |
R2 |
R3 |
R4 |
... |
|
a |
y |
0 |
0 |
... |
следующим образом:
T(1, 2)
Z(1)
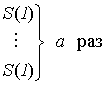
Pr
Новая программа Pr1, примененная к начальной конфигурации (*), вычисляет значение функции ga(y) = f(a, у) от одного аргумента у.
Теперь рассмотрим функцию s(a) = (Pr1),
сопоставляющую произвольному неотрицательному
целому числу a геделев номер программы Pr1.
Функция s всюду определена и по тезису Черча
вычислима. Кроме того, по построению fs(a)(у)
= f(a, у) для каждого .
Замечание 8.1. Сформулированную теорему называют также теоремой параметризации, поскольку она позволяет по заданной вычислимой функции f(x, у) и фиксированному параметру a найти геделев номер s(a) программы, вычисляющей функцию fs(a)(у) = f(a, у).
Доказанная выше теорема 8.1 является частным случаем более общей теоремы.
Теорема 8.2 (s-m-n-теорема). Пусть m, n -
натуральные числа, -
вычислимая функция с геделевым номером a.
Существует всюду определенная вычислимая
функция
такая, что
.
Доказательство сформулированного утверждения аналогично доказательству теоремы 8.1.
Замечание 8.2. Название теоремы 8.2 связано с
обозначением для
функций в формулировке теоремы.
Покажем теперь, как можно использовать s-m-n-теорему
для доказательства неразрешимости проблем. s-m-n-теорема
часто используется для сведения проблемы "" к другим проблемам.
Теорема 8.3. Проблема "" неразрешима.
Доказательство. Рассмотрим функцию
По тезису Черча функция f(x, y)
вычислима. Отсюда по s-m-n-теореме вытекает
существование всюду определенной вычислимой
функции s(x) такой, что . По определению функции f(x, y)
имеем:
.
Следовательно, истинность условия можно установить, определив
справедливость равенства
. Тем самым мы свели проблему "
" к проблеме "
". Поскольку первая из
них неразрешима, то неразрешима и вторая.
Замечание 8.3. Теорема 8.3 показывает, что в области проверки правильности компьютерных программ имеются принципиальные ограничения. В ней говорится о том, что не существует алгоритма проверки того, будет ли программа вычислять нулевую функцию. Несколько изменив доказательство теоремы 8.3, можно убедиться в том, что то же самое справедливо и для любой другой конкретной вычислимой функции.
Теорема 8.4. Проблема
неразрешима.
Доказательство. Допустим, что проблема разрешима. Тогда
разрешима и проблема
,
где c - индекс функции 0
. Однако, это противоречит теореме 8.3. Таким
образом, проблема
неразрешима.
Замечание 8.4. Из теоремы 8.4 следует, что вопрос о том, вычисляют ли две программы одну и ту же одноместную функцию, неразрешим. Важность этого результата для теоретического программирования очевидна.
Упражнения
8.1. Докажите, что не существует алгоритма, определяющего по тексту программы, будет ли эта программа вычислять некоторую конкретную вычислимую функцию.
8.2. 2. Покажите, что не существует всюду
определенной вычислимой функции f(x, y),
обладающей следующим свойством: если программа останавливается, то это
происходит за f(x, y) или меньше шагов.
Указание. Покажите, что если бы такая функция существовала, то проблема остановки была бы разрешима.
Естественно задаться вопросом, какие свойства вычислимых функций можно алгоритмически распознать по их программам. Оказывается, что никакие, кроме тривиальных. Доказательство этого факта содержится в теореме Райса.
Теорема 8.5 (теорема Райса). Пусть B -
непустое множество одноместных вычислимых
функций, не совпадающее со всем множеством одноместных вычислимых
функций. Тогда проблема "
" неразрешима.
Доказательство. Очевидно, что проблема "" разрешима тогда и
только тогда, когда разрешима проблема "
". Поэтому без потери
общности можно считать, что нигде не
определенная функция
не принадлежит B.
Выберем некоторую функцию и рассмотрим функцию
По тезису Черча функция f(x, y)
вычислима. Поэтому существует (по s-m-n-теореме)
всюду определенная вычислимая функция s(x)
такая, что . По
определению функции f(x, y) имеем:
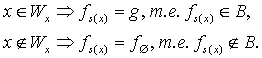
Таким образом, с помощью вычислимой функции s(x)
мы свели проблему ""
к проблеме "
".
Следовательно, проблема "
" неразрешима.
Дадим более содержательную формулировку теоремы Райса. Пусть Q некоторое свойство одноместных вычислимых функций. Свойство Q назовем нетривиальным, если существуют функции, обладающие свойством Q, и функции не обладающие этим свойством.
Все обычно рассматриваемые свойства являются нетривиальными. Примерами нетривиальных свойств служат следующие:
Так как вычислимые функции могут быть заданы программами их вычисления, то естественно возникает вопрос: можно ли по программе узнать, обладает ли соответствующая ей функция заданным нетривиальным свойством.
Теорема 8.6. Каково бы ни было нетривиальное свойство Q одноместных вычислимых функций, задача распознавания этого свойства алгоритмически неразрешима.
Доказательство. Пусть B - множество
одноместных вычислимых функций, обладающих
свойством Q. Множество B не пусто и не
совпадает со всем множеством одноместных
вычислимых функций. По теореме Райса проблема
"" неразрешима.
Из последней теоремы следует неразрешимость многих задач, связанных с программированием. Например, если имеется некоторая программа, то по ней, вообще говоря, ничего нельзя сказать о функции, реализуемой программой. По двум программам нельзя установить, реализуют ли они одну и ту же функцию, а это приводит к неразрешимости многих задач, связанных с эквивалентными преобразованиями и минимизацией программ. В любом алгоритмическом языке, какие бы правила синтаксиса там ни применялись, всегда будут иметься "бессмысленные" программы, задающие функции не определенные ни в одной из точек (эти программы нельзя обнаружить). Теорема Райса позволяет доказывать алгоритмическую неразрешимость многих задач, связанных с вычислениями на компьютерах.
Более подробно ознакомиться с формальными
подходами к вычислимости можно по книгам [4, 5].
ЛИТЕРАТУРА
1. Основы информатики и вычислительной техники. Пробное учебное пособие для средних учебных заведений. Ч. 1. Под ред. А. П. Ершова и В. М. Монахова. - М: Просвещение, 1985.
2. Ершов А. П. Алгоритмический язык . - Наука и жизнь. - 1985. - №11. - С. 61-63.
3. Абрамов С. А. Математические построения и программирование. - М.: Наука, 1978.
4. Катленд Н. Вычислимость. Введение в теорию рекурсивных функций. - М.: Мир, 1983.
5. Трахтенброт В. Л. Алгоритмы и вычислительные
автоматы. - М.: Советское радио, 1974.
INTRODUCTION IN THE THEORY OF ALGORITHMS
E. P. Emelchenkov, V. E. Emelchenkov
We consider main notions of algorithm theory. We research the
insolubility of many important problems for theoretical programming.
Кафедра информатики
Смоленский государственный педагогический университет
Поступила в редакцию 29.08.2000