УДК 51
О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ МОДЕЛЕЙ ФИЗИЧЕСКИХ ОБЪЕКТОВ НА ОСНОВАНИИ АНАЛИЗА ПРОТЕКАЮЩИХ В НИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ
© 2000 г. Л. Л. Лямец
Выбор и обоснование математической модели исследуемого физического объекта или явления является одной из важнейших задач анализа. В данной статье предложен один из способов построения математической модели физических объектов. Предлагаемая математическая модель позволяет не только прогнозировать поведение исследуемого физического объекта при различных внешних воздействиях, но и в определенной степени отражает его внутреннюю структуру и организацию.
Изучаемые в различных областях науки физические объекты (ФО) обычно имеют неоднородную внутреннюю структуру и сложную организацию. Энергетическое и агрегатное состояние ФО во многом определяется внешними условиями, в которых объект находится во время наблюдения за ним. В общем случае внешние условия изменяются с течением времени и, по сути, их можно рассматривать как некоторую совокупность внешних воздействий, оказывающих влияние на состояние и поведение ФО. Из общего числа внешних воздействий можно выделить одно или несколько воздействий, реакция на которые представляет наибольший научный и практический интерес. Для обеспечения чистоты экспериментов влияние других внешних воздействий должно быть по возможности устранено либо учтено при анализе результатов. Одна из наиболее часто решаемых задач научных исследований заключается в разработке и создании адекватной модели, позволяющей прогнозировать реакцию изучаемого ФО на определенное внешнее воздействие. Очевидно, что для одного и того же ФО можно указать несколько моделей, основанных на различных теоретических подходах. Наиболее удачными и более ценными с практической точки зрения являются модели, позволяющие не только прогнозировать поведение ФО при различных внешних воздействиях, но и в определенной степени отражающие его внутреннюю структуру и организацию. Такие модели позволяют выбрать и обосновать эквивалентную структурную схему изучаемого ФО, состоящую из простейших, хорошо изученных и теоретически обоснованных идеализированных элементов.
Первичную информацию о реакции
изучаемого ФО на определенное внешнее
воздействие можно получить в результате
проведения натурных экспериментов. Обычно перед
началом исследований ФО находится в
некотором стационарном состоянии. В
стационарном состоянии все физические процессы
в исследуемом ФО являются либо
периодическими функциями времени, либо
характеризуются постоянными величинами. Целью
натурных экспериментов является регистрация
реакции ФО на детерминированное входное
воздействие, вырабатываемое внешним источником
энергии. В качестве простейшего типового
внешнего воздействия удобно использовать
единичную ступенчатую функцию ![]() , которая также называется функцией
Хевисайда. Достоинством функции Хевисайда
является простота ее практической реализации. В
теории электрических цепей ступенчатое
воздействие
, которая также называется функцией
Хевисайда. Достоинством функции Хевисайда
является простота ее практической реализации. В
теории электрических цепей ступенчатое
воздействие ![]() соответствует,
например, подключению к исследуемой
электрической цепи источника постоянного
напряжения
соответствует,
например, подключению к исследуемой
электрической цепи источника постоянного
напряжения ![]() вольт. При
исследовании механических свойств полимеров
ступенчатое воздействие
вольт. При
исследовании механических свойств полимеров
ступенчатое воздействие ![]() может соответствовать ступенчатой
деформации образца на фиксированную величину
может соответствовать ступенчатой
деформации образца на фиксированную величину ![]() .
.
В результате воздействия на
исследуемый ФО функцией Хевисайда ![]() в нем возникает переходной
процесс, который связан с переходом от исходного
стационарного состояния к новому стационарному
состоянию. Исходному и новому стационарным
состояниям ФО соответствуют
определенные энергетические режимы. Изменение
энергетического режима ФО происходит за
счет энергии внешнего источника,
вырабатывающего ступенчатое воздействие.
Энергетическое состояние ФО не может
измениться скачком. Это легко показать на
следующем примере. Предположим, что энергия ФО
за промежуток времени
в нем возникает переходной
процесс, который связан с переходом от исходного
стационарного состояния к новому стационарному
состоянию. Исходному и новому стационарным
состояниям ФО соответствуют
определенные энергетические режимы. Изменение
энергетического режима ФО происходит за
счет энергии внешнего источника,
вырабатывающего ступенчатое воздействие.
Энергетическое состояние ФО не может
измениться скачком. Это легко показать на
следующем примере. Предположим, что энергия ФО
за промежуток времени ![]() изменилась
на величину
изменилась
на величину ![]() . Конечное
приращение энергии можно представить в виде
произведения мощности источника энергии
. Конечное
приращение энергии можно представить в виде
произведения мощности источника энергии ![]() на время
на время ![]() , за которое это приращение произошло,
, за которое это приращение произошло,
![]() .
.
Поскольку изменение скачком
предполагает очень маленький интервал времени ![]() , стремящийся к нулю, то в
этом случае мощность источника должна
стремиться к бесконечности
, стремящийся к нулю, то в
этом случае мощность источника должна
стремиться к бесконечности
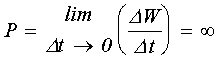 .
.
Однако реальные источники энергии обладают конечной мощностью. Следовательно, переходные процессы в реальных ФО не могут протекать за бесконечно малые промежутки времени.
Полученные в результате натурных
экспериментов графики переходных процессов
являются исходным материалом для анализа. Как
правило, после окончания экспериментов графики
переходных процессов получают в виде временных
диаграмм, зафиксированных при помощи
специальных регистрирующих приборов, или в виде
таблиц, содержащих значения переходного
процесса в определенные моменты времени,
измеренные с момента начала наблюдения через
фиксированный временной интервал ![]() .
.
Для анализа экспериментальных графиков переходных процессов их целесообразно аппроксимировать удобной с практической точки зрения математической функцией. Аппроксимация позволяет получить адекватную математическую модель переходной характеристики. Решение общей задачи аппроксимации состоит из трех самостоятельных этапов. На первом этапе необходимо выбрать и обосновать функциональную структуру аппроксимирующего математического выражения. На втором этапе необходимо по имеющимся экспериментальным данным вычислить коэффициенты аппроксимации для выбранной математической функции. На третьем этапе целесообразно оценить точность аппроксимации.
Выбор и обоснование функциональной структуры аппроксимирующего математического выражения не имеют однозначного решения. К аппроксимирующей функции предъявляются следующие требования. Она должна быть по возможности наиболее простой, то есть выраженной через простые математические функции. Только в этом случае будет удобно пользоваться формулой аппроксимации для выполнения дальнейших практических расчетов и это даст возможность использовать полученные результаты в конкретных технических решениях. Кроме того, аппроксимирующая функция должна иметь компактную форму записи. Очевидно, что громоздкое аппроксимирующее выражение существенно усложняет анализ исследуемого физического процесса и увеличивает трудоемкость выполняемых вычислительных операций. Следует помнить, что аппроксимация переходной характеристики не самоцель, а лишь инструмент для изучения и исследования процессов в ФО.
Требования, предъявляемые к аппроксимирующей функции, очень часто вступают в противоречие с точностью аппроксимации. Можно очень точно описать экспериментальную характеристику каким либо аналитическим выражением. Но если это выражение окажется математически сложным, да и к тому же громоздким, то вряд ли можно считать задачу аппроксимации решенной. При выборе аппроксимирующей функции следует отдать предпочтение такой математической модели, которая имеет достаточно простую и компактную форму, отражает определенный физический смысл и график которой достаточно точно воспроизводит полученную в результате эксперимента реализацию переходного процесса.
До начала переходного процесса и после
его окончания физические процессы в исследуемом ФО
характеризуются либо постоянными величинами,
либо периодическими функциями. В переходном
режиме физические процессы в ФО являются
непериодическими функциями. Теоретически
переходные процессы могут иметь бесконечно
большую продолжительность. Однако на практике
для большинства ФО различной природы
можно считать, что переход от исходного к новому
стационарному состоянию происходит за конечный
промежуток времени. Это означает, что
непериодические функции, существующие во время
переходного процесса, являются затухающими.
Следовательно, для математического описания
графиков переходных процессов необходимо
использовать аппроксимирующие функции, имеющие
убывающий характер. Например, известно, что в
линейных системах различной природы переходные
процессы описываются убывающими
экспоненциальными функциями. В связи с этим
можно предположить, что для аппроксимации
экспериментальных переходных характеристик ![]() исследуемых ФО
можно использовать экспоненциальный полином
исследуемых ФО
можно использовать экспоненциальный полином
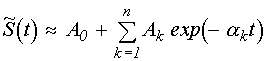 . (1)
. (1)
В выражении (1) совокупность
убывающих экспоненциальных функций 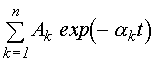 отражает характер протекания
переходного процесса. В зависимости от значений
коэффициентов
отражает характер протекания
переходного процесса. В зависимости от значений
коэффициентов ![]() и
и ![]() переходной режим может
носить колебательный или апериодический
характер. Величина
переходной режим может
носить колебательный или апериодический
характер. Величина ![]() характеризует
состояние ФО после окончания переходного
процесса. Задача аппроксимации переходного
процесса сводится к вычислению коэффициентов
характеризует
состояние ФО после окончания переходного
процесса. Задача аппроксимации переходного
процесса сводится к вычислению коэффициентов ![]() ,
, ![]() и
и
![]() . Методика вычисления
коэффициентов экспоненциального полинома (1)
подробно изложена в работе [1]. В зависимости от
значений коэффициентов аппроксимации
. Методика вычисления
коэффициентов экспоненциального полинома (1)
подробно изложена в работе [1]. В зависимости от
значений коэффициентов аппроксимации ![]() и
и ![]() выражение
(1) может иметь апериодический или
колебательный экспоненциально затухающий
характер.
выражение
(1) может иметь апериодический или
колебательный экспоненциально затухающий
характер.
Для оценки точности аппроксимации
экспериментально полученной реализации
переходного процесса аналитическим выражением (1)
можно использовать условие среднеквадратичного
приближения. Это условие состоит в том, что
аппроксимирующая функция не должна отличаться
от аппроксимируемой реализации переходного
процесса более чем на величину ![]() , т. е. должно выполняться требование
, т. е. должно выполняться требование
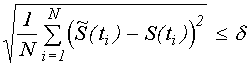 . (2)
. (2)
Для практического использования
условия (2) необходимо по исследуемой
реализации переходного процесса ![]() определить значения
определить значения ![]() в дискретные моменты времени
в дискретные моменты времени ![]() , следующие друг за другом
через временной интервал
, следующие друг за другом
через временной интервал ![]() . Величина
. Величина ![]() соответствует
количеству взятых дискретных отсчетов. Для тех
же самых моментов времени
соответствует
количеству взятых дискретных отсчетов. Для тех
же самых моментов времени ![]() необходимо вычислить значения
аппроксимирующей функции
необходимо вычислить значения
аппроксимирующей функции ![]() . Величина
. Величина ![]() характеризует
точность аппроксимации и определяется в каждом
конкретном случае из практических соображений.
характеризует
точность аппроксимации и определяется в каждом
конкретном случае из практических соображений.
При увеличении количества экспоненциальных составляющих в аналитическом выражении (1) точность аппроксимации будет возрастать. Неограниченное увеличение точности аппроксимации не имеет практического смысла. Условие среднеквадратичного приближения позволяет не только оценить точность аппроксимации, но и дает возможность определить оптимальное количество экспоненциальных составляющих в выражении (1).
Из теории известно, что переходные
процессы в линейных системах можно аналитически
описать при помощи дифференциальных уравнений,
составленных на основе фундаментальных
физических законов. Простейшие линейные системы,
содержащие один энергоемкий элемент, при
воздействии на них функции Хевисайда
описываются линейными неоднородными
дифференциальными уравнениями первого порядка.
Решение таких уравнений содержит
экспоненциальную функцию и описывает переходной
процесс в системах первого порядка. Линейные
системы, содержащие два энергоемких элемента,
при воздействии на них функции Хевисайда
описываются линейными неоднородными
дифференциальными уравнениями второго порядка.
Решение таких уравнений описывает переходной
процесс в системах второго порядка и содержит
сумму двух экспоненциальных функций ![]() . В общем случае количество
энергоемких элементов в линейной системе влияет
на порядок дифференциального уравнения.
Количество экспоненциальных функций в решении
дифференциального уравнения зависит от его
порядка.
. В общем случае количество
энергоемких элементов в линейной системе влияет
на порядок дифференциального уравнения.
Количество экспоненциальных функций в решении
дифференциального уравнения зависит от его
порядка.
Очевидно, что количество
экспоненциальных функций ![]() в формуле (1) можно связать с
количеством энергоемких идеализированных
элементов. Это предположение дает возможность
рассматривать исследуемый ФО как
линейную систему
в формуле (1) можно связать с
количеством энергоемких идеализированных
элементов. Это предположение дает возможность
рассматривать исследуемый ФО как
линейную систему ![]() -го
порядка, содержащую
-го
порядка, содержащую ![]() энергоемких
идеализированных элементов, в которых
переходной процесс, вызванный действием функции
Хевисайда, описывается экспоненциальным
законом. Следовательно, можно сделать вывод о
том, что результаты аппроксимации позволяют
представить исследуемый ФО в виде модели,
состоящей из совокупности
энергоемких
идеализированных элементов, в которых
переходной процесс, вызванный действием функции
Хевисайда, описывается экспоненциальным
законом. Следовательно, можно сделать вывод о
том, что результаты аппроксимации позволяют
представить исследуемый ФО в виде модели,
состоящей из совокупности ![]() простейших структурных элементов первого
порядка. Этот вывод имеет большое практическое
значение. Особенно важное значение полученный
результат имеет при анализе ФО,
представляющих собой системы с распределенными
параметрами. Аппроксимация и анализ переходных
процессов в таких системах позволяют построить
формальную эквивалентную модель в виде системы с
сосредоточенными параметрами, содержащими
определенное количество энергоемких элементов.
простейших структурных элементов первого
порядка. Этот вывод имеет большое практическое
значение. Особенно важное значение полученный
результат имеет при анализе ФО,
представляющих собой системы с распределенными
параметрами. Аппроксимация и анализ переходных
процессов в таких системах позволяют построить
формальную эквивалентную модель в виде системы с
сосредоточенными параметрами, содержащими
определенное количество энергоемких элементов.
ЛИТЕРАТУРА
ABOUT POSSIBILITY OF MATHEMATICAL MODELS CONSTRUCTION OF PHYSICAL OBJECTS ON THE BASIS OF THE ANALYSIS OF ITS PROCCEDING TRANSITION PROCESSES
L. L. Lamec
The choice and substantiation of mathematical model of researched physical object or phenomena is one of major tasks of the analysis. In given clause one of ways of construction of mathematical model of physical objects is offered. The offered mathematical model allows not only to predict behaviour of researched physical object at various external influences, but also in the certain degree reflects his(its) internal structure and organization.
Комитет науки и технологий
администрации Смоленской области
Поступила 4.10.2000.