УДК 519.1

© 2001 г. В. И. Левин

За долгие годы существования люди накопили богатый положительный опыт применения математики в естественных науках – физике, химии, астрономии, геологии, а также в технике. Однако в гуманитарных и общественных науках дело обстояло иначе. Здесь, до последнего времени были распространены словесные описания изучаемых явлений, что часто приводило к результатам, не поддающимся сравнительному анализу, не говоря уже о самом характере изложения – многословном и нередко неоднозначным по смыслу. В то же время многие, даже сложные объекты в указанных науках вполне поддаются описанию адекватными математическими моделями. Язык математики может логично, строго и однозначно описывать конструкции, которые раньше излагались только словесно. Более того, благодаря компактности этот язык позволяет в ряде случаев вскрывать неизвестные ранее закономерности в изучаемых объектах. Эти особенности позволили математическим методам проникнуть за последние десятилетия во многие общественные и гуманитарные науки – экономику, социологию, психологию, лингвистику, историю, юриспруденцию и т.д. Начало применения математических методов к изучению исторических процессов относится к 60-м годам 20 в. Большинство этих методов базируется на теории вероятностей и математической статистике [1]. При этом предполагается, что отдельные события, составляющие исторический процесс, являются случайными событиями. Такое предположение кажется нам спорным – ведь случайным может быть только событие, которое можно повторить неограниченное число раз (например, бросание монеты, игральной кости и т.д.), а все исторические события уникальны. Таким образом, возникает интерес к иным математическим методам исследованиям исторических процессов, учитывающим уникальность (неповторимость) исторических процессов и не базирующимся на теории вероятностей и математической статистике. В работах [2,3] был предложен оригинальный метод математического моделирования разнообразных исторических процессов, базирующийся на теории автоматов и математической логике и не использующий вероятностно-статистических представлений, что позволяет лучше учесть уникальность изучаемых процессов. В настоящей работе этот метод применен для математического моделирования процесса последовательного возникновения и прекращения войн (потока войн).

1. Постановка задачи

Пусть имеется некоторое число регионов (частей света, стран, штатов и т.д.), в которых происходят конкретные исторические события, а именно, войны. В каждом конкретном регионе войны происходят, согласно предположению, в соответствующей последовательности временных интервалов, причем различные интервалы не пересекаются и каждый содержит ровно одну войну – от момента ее начала (левая граница интервала) до момента окончания (правая граница). Таким образом, каждый регион имеет свой поток последовательно возникающих и прекращающихся войн. Мы будем изучать суммарный поток войн, получаемый путем суммирования описанных региональных потоков. Нас будут интересовать различные количественные характеристики суммарного потока войн, знание которых позволяет выявить основные закономерности процесса последовательного возникновения и прекращения войн на земле. При этом, разумеется, вначале должно быть установлено, что такие закономерности существуют.

Имеется две трудности, связанные с решением поставленной задачи. Первая – выбор подходящих, достаточно представительных характеристик суммарного потока войн. Вторая трудность – необходимость эффективного вычисления указанных характеристик при возможном большом числе региональных потоков войн, образующих суммарный поток, и большом числе войн в отдельных региональных потоках. Мы покажем, что использование предлагаемого автоматно-логического подхода к математическому моделированию потоков войн позволяет естественным образом преодолеть обе указанные трудности. Заметим еще, что при больших регионах условие: одна война в одном интервале регионального потока войн – может нарушаться. В этих случаях надо разбить регион на несколько подрегионов. Наше исследование проводится применительно к набору наиболее известных в мире войн за последние 2500 лет

Пусть имеется некоторое число регионов, в которых происходят однородные по своей природе исторические события – войны. Пусть в произвольном -м регионе () эти события происходят в следующих последовательных временных интервалах - в каждом интервале по одному событию. При этом левая граница указывает момент начала, а правая – момент окончания соответствующего события – войны. Будем изучать суммарный поток войн, получаемый суммированием потоков войн в отдельных регионах. . Нас будут интересовать различные количественные характеристики суммарного потока войн. Для их нахождения поставим во взаимно-однозначное соответствие заданному потоку войн в -м регионе двоичный процесс-индикатор , где двоичная переменная x=1 означает наличие, а x=0 – отсутствие войны в -м регионе в соответствующий момент времени . Изучаемый суммарный поток войн исчерпывающе характеризуется набором двоичных процессов , где двоичная переменная означает, что суммарный поток в данный момент времени состоит из одновременно происходящих войн, а - что этот поток состоит из , где , одновременно происходящих войн. Двоичные процессы , естественно называть спектральными временными функциями суммарного потока войн, так как временные интервалы их единичных значений - это интервалы, в которых суммарный поток войн содержит то или иное конкретное число одновременно происходящих войн. Вектор-функцию , состоящий из всех спектральных функций, назовем спектром суммарного потока войн. Кроме спектра, суммарный поток событий можно исчерпывающе охарактеризовать (n+1)-ичной функцией потока y(t), принимающей значения . При этом , означает, что суммарный поток в данный момент времени содержит ровно одновременно происходящих войн. Оба способа количественного описания суммарного потока войн эквиваленты: по спектру можно всегда вычислить функцию плотности суммарного потока, используя для этого формулу

, (1)

а по функции плотности суммарного потока - его спектр, используя формулу,

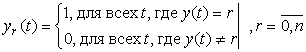. (2)

В дальнейшем в основу количественного описания суммарного потока войн положим его спектр.

Для нахождения спектральных функций , построим соответствующую автоматную модель [2,3]. Из условия задачи (§1) следует, что в любом -м регионе в любой момент времени может происходить только одна война либо не происходить ничего. Поэтому для того, чтобы в данный момент времени суммарный поток войн от всех регионов содержал происходящих одновременно войн, необходимо и достаточно, чтобы ровно в из регионов в этот момент происходила война. Используем теперь симметрические булевы логические функции различных индексов от двоичных переменных [4]. Любая такая функция равна 1, если ровно из ее переменных (безразлично, какие именно), равны 1, и равно 0 в остальных случаях. Ясно, что зависимость неизвестных двоичных переменных , описывающих состояние изучаемой системы в произвольный момент времени, , от известных двоичных переменных , описывающих состояния регионов в указанный момент, выражается с помощью введенных функций в виде

. (3)

Функции в (3) естественно называть функциями состояния изучаемой системы. Соотношения (3) между состояниями регионов и состоянием всей системы в один и тот же произвольный момент времени , описываемые с помощью функций состояния системы , являются абстрактной математической моделью изучаемой системы. Эта модель - некоторый динамический автомат без памяти [5]. Такой автомат реализуется структурно соответствующей комбинационной логической схемой (рис. 1), которая, таким образом, является структурной математической моделью изучаемой системы. Входные процессы схемы-модели рис. 1 в соответствии с условиями задачи (§2) имеют вид следующих последовательностей импульсов и пауз в указанных скобками интервалах

. (4)

Благодаря построенной автоматной математической модели изучаемой системы поставленная задача нахождения спектральных процессов , определяющих суммарный поток войн, по известным процессам , задающим потоки войн в отдельных -х регионах, сводится к стандартной задаче динамической теории автоматов [5]. А именно, по построенной комбинационной логической схеме рис. 1, реализующей набор булевых логических функций состояния системы (3), и заданным входным процессам схемы , найти выходные процессы схемы . 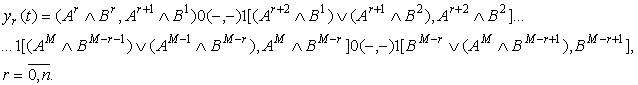Последняя задача решается с использованием следующей формулы динамической теории автоматов, связывающей входные и выходной двоичные -процессы комбинационной логической схемы, реализующей на выходе функцию входов [5]:

(5)

В формуле (5) - логический определитель ранга , составленный из моментов всех скачков вида во входных процессах схемы , - логический определитель ранга , составленный из моментов всех скачков вида во входных процессах схемы , и - операции дизъюнкции и конъюнкции непрерывной логики, - общее число импульсов во всех входных процессах . Здесь логическим определителем ранга называется функция, отображающая множество всех элементов определителя в его -й по возрастанию элемент . Логический определитель вычисляется либо согласно приведенному его определению, либо по специальным формулам [5], с помощью операций и .

Мы попытаемся изучить описанным в §2 методом поток наиболее известных в истории человечества войн, произошедших за последние 2500 лет, с 500 г. до н.э. по 2000 г. н.э. Этот поток включает 88 войн, представленных в таблице 1. Таблица заимствована нами из энциклопедического справочника [6], с добавлением I Кавказской войны (№ 53 в табл. 1), а также Советско-афганистанской (№ 85), II и III Кавказских (№№ 86, 87) и НАТО- югославской (№ 88) войн. Для того, чтобы применить метод §2, мы должны описать поток войн, представленный в табл. 1, в терминах общей постановки задачи исследования суммарного потока войн §1.

1) Выделяем конкретные регионы, в которых происходили войны. Таких регионов, очевидно, 4: страны древнего мира , Европа , Россия , Азия совместно с Африкой и Америкой , 2) Проверяем условие непересечения временных интервалов различных войн, происходивших в одном и том же регионе. Для региона это условие не выполнено: 7 войн, происходивших в нем (войны №№ 1-6, 8 табл. 1), относятся к различным интервалам времени, но войны 6 и 7 пересекаются во времени. Также для регионов это условие не выполнено. Так, для региона пересекаются во времени следующие подмножества войн: {9,10}, {21,22}, {27,29}, {29,30}, {33,34}, {34,36}, {70,71}, {71,72}, для региона Р – подмножества {19,20}, {26,28}, {31,32}, {40,41}, {44,47,48}, {44,47,50}, {53,54,55}, {53,58}, для региона – подмножества {65,66}, {79,80}, {80,81}, {80,82}, {82,83}. Из приведенных данных видно, что в регионах , и пересекаются во времени лишь некоторые пары происходящих там войн, а в регионе – как некоторые пары, так и некоторые тройки войн. Теперь для того, чтобы выполнить требуемое постановкой задачи (§1) условие непересечения во времени различных войн, происходящих в одном и том же регионе, необходимо разбить множества войн, происходящих в регионах , и , на два подмножества каждое, так, чтобы в этих подмножествах (им отвечают подрегионы и региона , подрегионы и региона и подрегионы и региона ) войны не пересекались во времени. Аналогично, необходимо разбить множество войн, происходящих в регионе , на три подмножества, так чтобы в этих подмножествах (им отвечают подрегионы региона ) войны не пересекались во времени. Все заданные табл. 1 войны, с учетом указанных необходимых разбиений множеств войн и соответствующих им разбиений регионов, представлены в табл. 2.

Мы изучим суммарный поток войн, представленных в табл. 1, используя в качестве количественных характеристик этого потока его спектр и плотность (§2).

Построим автоматную математическую модель изучаемого потока войн, с целью нахождения его количественных характеристик и . Согласно §2, эта модель после ее структурной реализации имеет вид комбинационной логической схемы рис. 1 с числом входов , соответствующим числу выделенных подрегионов (см. табл. 2). Входные процессы схемы , моделирующие потоки войн в соответствующих подрегионах (см. табл. 2), известны и могут быть записаны в форме (4) последовательностей импульсов и пауз (длят простоты записи паузы опущены)

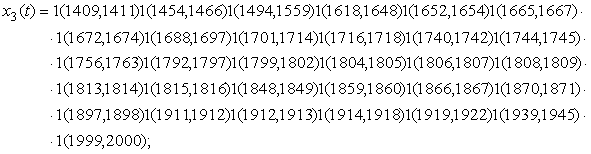
(6)

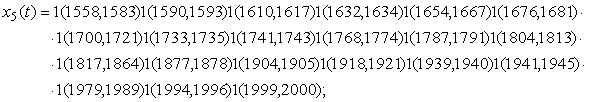
В записанных процессах отрицательные числа соответствуют моментам (годам) возникновения и прекращения войн, происходивших до н.э., а положительные числа – соответствующим моментам (годам), для войн, происходивших после наступления н.э. Далее, для войн №№ 45, 52, 60, 62, 67, 72, 82, происходивших в пределах одного календарного года, добавлен еще один год – предыдущий или последующий. Это вызвано тем, что, если не делать этого, длительности указанных войн формально будут равны нулю (мы не учитываем месяцы, а только годы!), т.е. они не будут учтены в общем потоке войн. При добавлении указанного года выбирается тот из двух возможных вариантов (предыдущий или последующий), который 1) не дает пересечения во времени рассматриваемой войны с другими войнами в данном регионе и 2) минимизирует число дополнительно возникших пересечений данной войны с войнами в других регионах.

Построенная автоматная математическая модель изучаемого потока войн показана на рис. 2.

Приступим к решению задачи нахождения спектральных процессов , определяющих, согласно (1) искомую плотность потока войн, по известным процессам , задающим потоки войн в отдельных -х регионах. Используем формулу (5). В рассматриваемом случае число процессов [число подрегионов] и общее число импульсов в этих процессах, согласно формулам (6), равно

. (7)

Учтем еще следующие свойства логических определителей [5]

. (8)

Первое свойство (8) следует из того, что, согласно его смыслу, логический определитель ранга должен быть меньше любого его элемента, поэтому при любых порядковых вычислениях его можно считать равным . Аналогично, второе свойство (8) следует из того, что определитель ранга (где - общее число элементов определителя) должен быть больше любого его элемента, так что любых порядковых вычислениях его можно считать равным . Третье и четвертое свойства (8) следуют из того, что, во-первых, логические определители и одного и того же ранга , фигурирующие в формуле (5), находятся в соотношении и, во-вторых, определитель есть возрастающая функция ранга. В результате учета свойств (8) и того, что в нашем случае , из общей формулы (5) получим следующие конкретные выражения спектральных процессов , в виде последовательностей импульсов и промежуточных пауз между ними

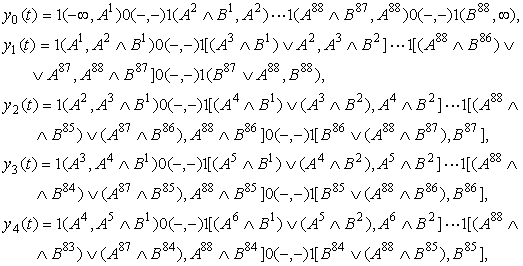
(9)

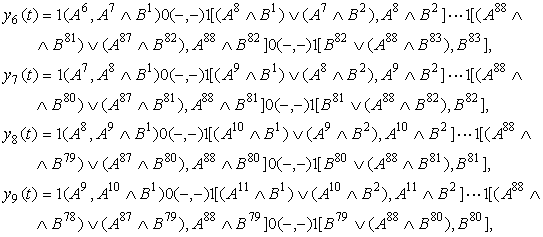
Вычислим выражения (9), используя указанные выше правила вычисления логических определителей и конкретный вид фигурирующих в (9) определителей и , соответствующий виду (6) входных процессов нашей расчетной схемы-модели рис. 1:

Результаты вычислений представлены в табл. 3. В левом столбце табл. 3 указаны последовательные интервалы времени, в каждом из которых все спектральные процессы , имеют постоянное значение. В правом столбце этой таблицы содержатся соответствующие значения всех спектральных процессов , а также суммарного процесса . При этом непосредственно указаны только значения процесса , но они, согласно формуле (2), определяют и значения всех процессов . Например, если , то при .

Построенный по табл. 3 график суммарного процесса , который согласно §1 является плотностью суммарного потока войн, показан на рис. 3.

Проанализируем изучаемый поток войн, используя для этого его количественные характеристики, найденные в §4, в сочетании с исходными данными (табл. 1). С этой целью найдем еще некоторые вторичные количественные характеристики потока, опирающиеся на уже известные характеристики и исходные данные. Все приведенные ниже вторичные характеристики являются усредненными и вычисляются для каждого века в отдельности.

Начнем с характеристики - среднего времени, приходящегося на одну войну, - вычисляемой по формуле

. (10)

Здесь - число войн в том веке, для которого вычисляется . Это число определяется по табл. 1. Очевидно, что и есть некоторые количественные характеристики частоты войн – чем больше и меньше , тем чаще происходят войны. Следующая характеристика - средний интервал времени между соседними войнами – вычисляется по формуле

, (11)

где - промежуток времени между центрами -й пары соседних войн (определяется по табл. 1, с учетом уточнения длительности некоторых войн, сделанного в §4), - число войн в том веке, для которого вычисляется . Суммирование в (11) ведется по всем парам войн, относящихся к данному веку (если некоторая война происходит частично в данном, а частично в соседнем веке, то мы оперируем только с той частью, которая происходит в данном веке, рассматривая ее как отдельную войну). есть некоторая другая количественная характеристика частоты войн, чем , отличающаяся от учетом не только числа войн , но и их взаиморасположения. К характеристикам и примыкает характеристика - средняя длительность одной войны, вычисляемая по формуле

, (12)

где - длительность -й войны (определяется по табл. 1, с учетом уточнения длительности некоторых войн, сделанного в §4), ), - число войн в том веке, для которого вычисляется . Суммирование ведется по всем войнам, относящихся к данному веку (если какая-то война охватывает два века, ее учитываем так же, как в формуле (11)). Очевидно, что есть количественная характеристика длительности войн века.

Следующая пара количественных характеристик потока войн – доля времени мира и доля времени войн , определяемые для каждого отдельного века по формулам

, (13)

где и - общее время мира и общее время войн в течение рассматриваемого века, определяемые из табл. 3. Ясно, что

, (14)

в связи с чем из двух характеристик и достаточно определить какую-нибудь одну. и являются количественными характеристиками насыщенности времени войнами, причем соответствует максимальной, а - минимальной насыщенности.

Последняя пара вторичных количественных характеристик потока войн: - число участков концентрации военного напряжения и - средний интервал времени между соседними участками концентрации военного напряжения. Здесь под участком концентрации военного напряжения понимается интервал времени, на котором характеристика достигает локального максимума, большего единицы. Другими словами, это интервал, на котором происходит одновременно рекордное число (два или более) войн, так, что в предшествующем и следующем годах происходит одновременно меньше войн, чем в данном интервале. Характеристика определяется по табл. 3 или по графику рис. 3, а характеристика - по формуле

, (15)

где - интервал времени между центрами -й пары соседних участков концентрации военного напряжения, и суммирование ведется по всем парам участков, относящихся к данному веку. Интервалы определяются по табл. 3 или по графику рис. 3. Очевидно, что и есть некоторые количественные характеристики степени военного напряжения – чем больше (меньше ), тем выше эта степень для рассматриваемого века.

Результаты расчета характеристик приведены в табл. 4, а соответствующие графики – на рис. 4.

Из графиков на рис. 4 можно сделать следующие выводы.

1. Характеристика - число войн, происходящих в течение одного века, до н.э. весьма незначительно и является практически постоянной величиной. Однако, начиная, по крайней мере, с 14 в. н.э., это число становится функцией, существенно зависящей от времени и практически монотонно возрастающей, достигая при этом больших значений .
2. Аналогично поведение другой характеристики - - числа участков концентрации военного напряжения, приходящихся на один век: до н.э. оно незначительно и практически постоянно , а начиная с 14 в. н.э. становится практически монотонно возрастающей функцией времени, достигающей существенных значений .
3. Характеристика - среднее время, приходящееся на одну войну, - является существенной функцией времени как в период до н.э., так и после него. При этом до н.э. превалирует тенденция возрастания величины вплоть до лет, а после 14 в. н.э. – тенденция убывания , вплоть до лет.
4. Характеристика - средний интервал времени между соседними войнами – в период до н.э. изменяется резко скачкообразно (между значениями и ), а с 15 в. н.э. – практически монотонно убывает, достигая минимального значения .
5. Практически такое же поведение у характеристики - средней длительности одной войны. Величина в период до н.э. изменяется скачкообразно в границах от до , а с 14 в. н.э. практически монотонно убывает, достигая минимального значения .
6. Характеристика - средний интервал времени между соседними участками концентрации военного напряжения – является практически монотонной функцией времени во всем диапазоне ее существования (с 17 в. н.э. по 20 в. н.э.), достигая в итоге минимального значения .
7. Поведение характеристики - доли времени мира – обнаруживает резко скачкообразное изменение в период до н.э. (между крайними значениями и ), монотонное убывание в раннее средневековье (с 14 в. по 16 в.) и монотонное возрастание в новое время (после 16 века), с финальным значением , практически совпадающим со значением в 14 в. - .
8. Аналогично поведение двойственной к характеристики - доли времени войны: в период до н.э. величина изменяется резко скачкообразно (крайние значения и ), в средние века она монотонно возрастает, а в новое время монотонно убывает, достигая финального значения , практически совпадающего со значением в 14 в. – .
9. Не обнаружено никакой периодичности в поведении всех вышеупомянутых характеристик, что побуждает усомниться в справедливости неоднократных высказываний о периодичности потока войн. Напротив, поведение этих характеристик свидетельствует о монотонном характере последовательности войн, начиная, по крайней мере, с 16 века.

10. Упомянутая в п. 9. Монотонность проявляется в непрерывном росте частоты войн и частоты участков концентрации военного напряжения , уменьшении интервалов времени между войнами и, как следствие, длительности войн . В то же время доли времени мира и времени войны убывая (возрастая) с 14-го по 16-й век и возрастая (убывая) с 16-го по 20-й век, в целом за весь этот период остаются практически неизменными. Эта общая картина войн свидетельствует в пользу библейских пророчеств о движении мира к своему концу из-за неспособности людей извлекать уроки из истории.

11.И все же, как видно из табл. 4 и графиков на рис. 4., у нас есть надежда: в 20-м веке 7 из 8 количественных характеристик потока войн улучшили свои значения. А именно, уменьшилась частота войн и частота участков концентрации военного напряжения , увеличились интервалы времени между войнами и интервалы времени между участками концентрации военного напряжения , увеличилась доля времени мира и уменьшилась доля времени войны . Возможно, это признак пробуждения человечества, его желания начать, наконец, управлять историческим процессом в своих интересах.

Представленный в статье материал – первый опыт применения автоматно-логического моделирования истории [2,3] к конкретному историческому процессу – потоку наиболее известных войн за последние 2500 лет. Этот опыт подтверждает предварительные выводы [2], что с помощью достаточно простых вычислений можно получить количественные характеристики изучаемого исторического процесса и на этой основе строить правильное понимание этого процесса и его разумное объяснение Возможно, что на этом пути удастся наметить какие-то конструктивные методы управления историческими процессами. Важное значение имеют также детальные исследования различных конкретных исторических процессов (войн, кризисов, революций и т.д.), выполненные аналогично представленному в этой статье. Такие исследования позволили бы, с одной стороны, попытаться лучше понять указанные процессы, а с другой – обстоятельно проверить работоспособность предложенного подхода.

1. Коваленко И.Д. (ред.) Количественные методы в исторических исследованиях. М.: Высшая школа, 1984.
2. Левин В.И. Математическое моделирование социально-экономических процессов (автоматно-логические методы и модели). Пенза: Изд-во Пенз. технол. ин-та, 1997.
3. Левин В.И. Математическое моделирование потока исторических событий методами теории автоматов// Гуманитарные науки и современность. Вып. 5. Пенза: Изд-во Пенз. гос. ун-та, 1999.
4. Поспелов Д.А. Логические методы анализа и синтеза схем. М.: Энергия, 1987.
5. Левин В.И. Теория динамических автоматов. Пенза: Изд-во пенз. гос. техн. ун-та, 1995.
6. Альфа и Омега. Таллинн: изд-во “Валгус”, 1988.

Таблица заимствована (с небольшими добавлениями) из книги [6]. Обозначения: Д – войны древнего мира, Е – войны в Европе, Р – войны, которые вела Россия, А – войны в Азии, Африке и Америке.

Таблица 2

Таблица 3

Таблица 4

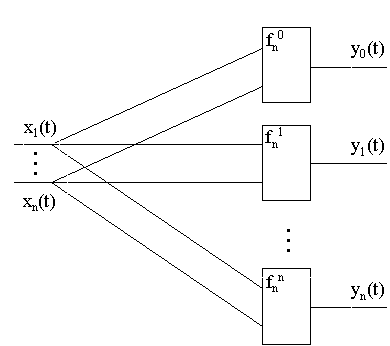
Рис. 1. Структурная модель системы

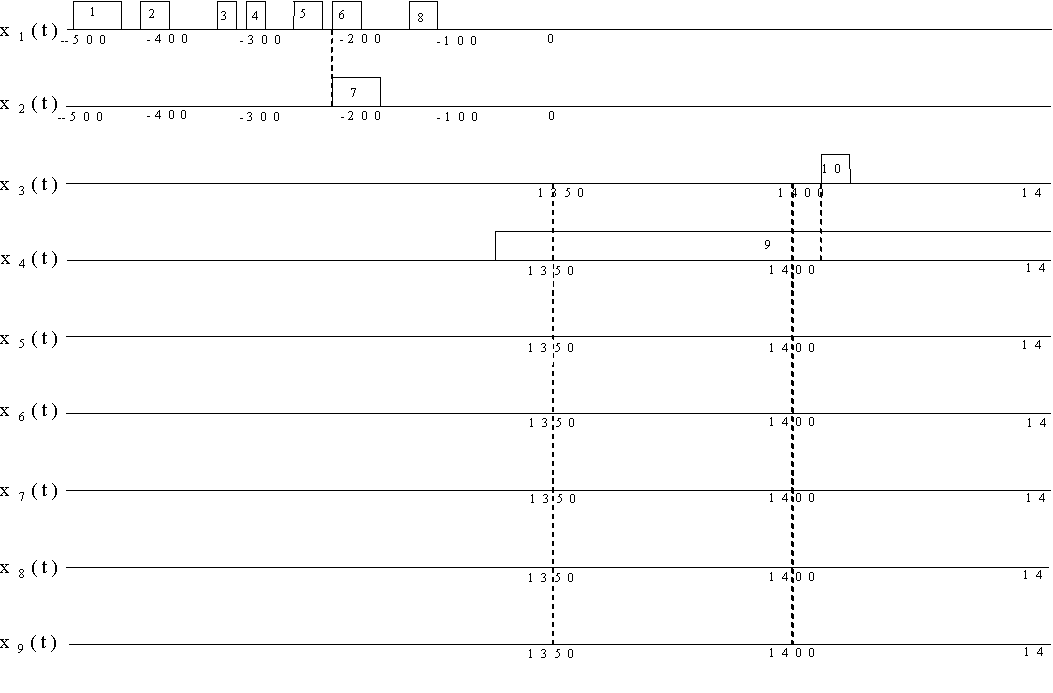
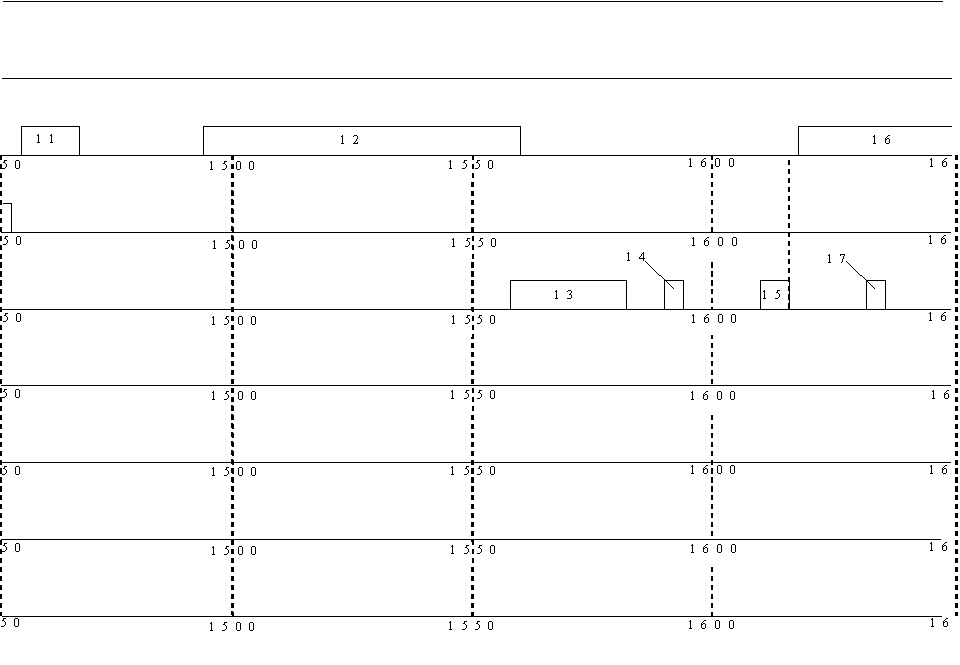
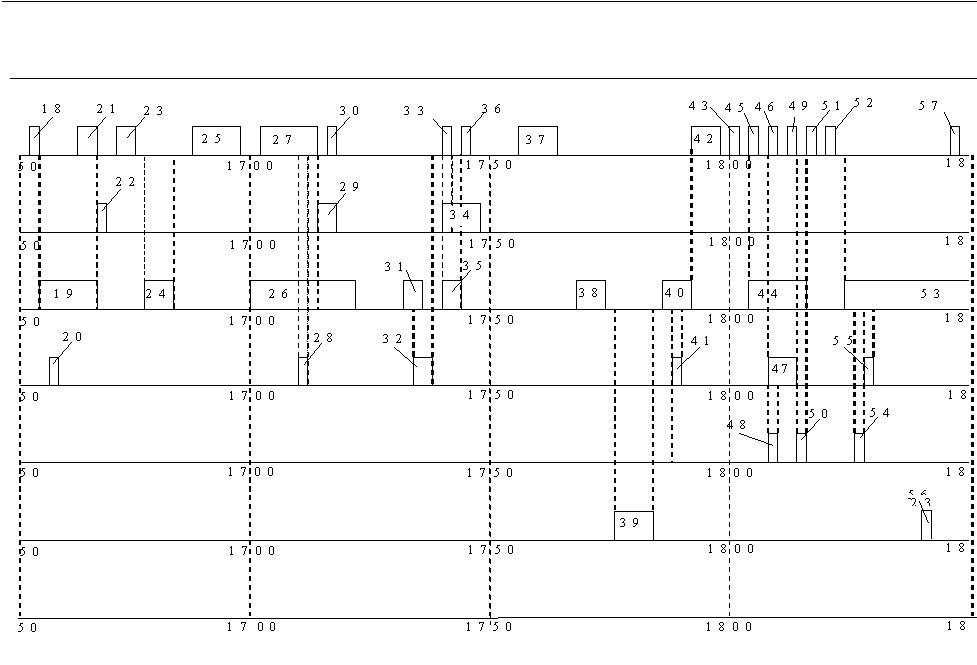
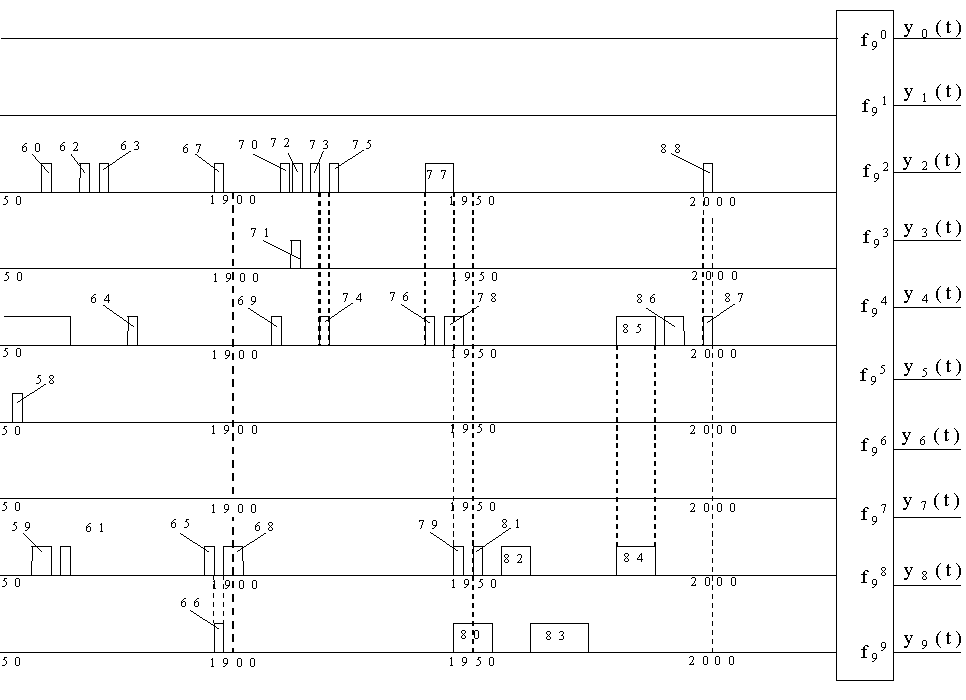
Рис. 2. Структурная автоматная математическая модель изучаемого потока войн, заданного табл.1 Входные процессы модели задаются формулами (6); они моделируют потоки войн в регионах 1,2,…,9 в соответствии с табл. 2 и показаны на рисунке в виде импульсных потоков с соответствующими номерами импульсов. Например, процесс показан в виде потока с импульсами 1, 2, 3, 4, 5, 6, 8, интервалы действия которых совпадают в временными интервалами войн 1, 2, 3, 4, 5, 6, 8 из табл. 1. Выходные процессы модели определяются формулами (9), в которых используются входные процессы . Они моделируют спектральные составляющие плотности суммарного потока войн всех подрегионов.

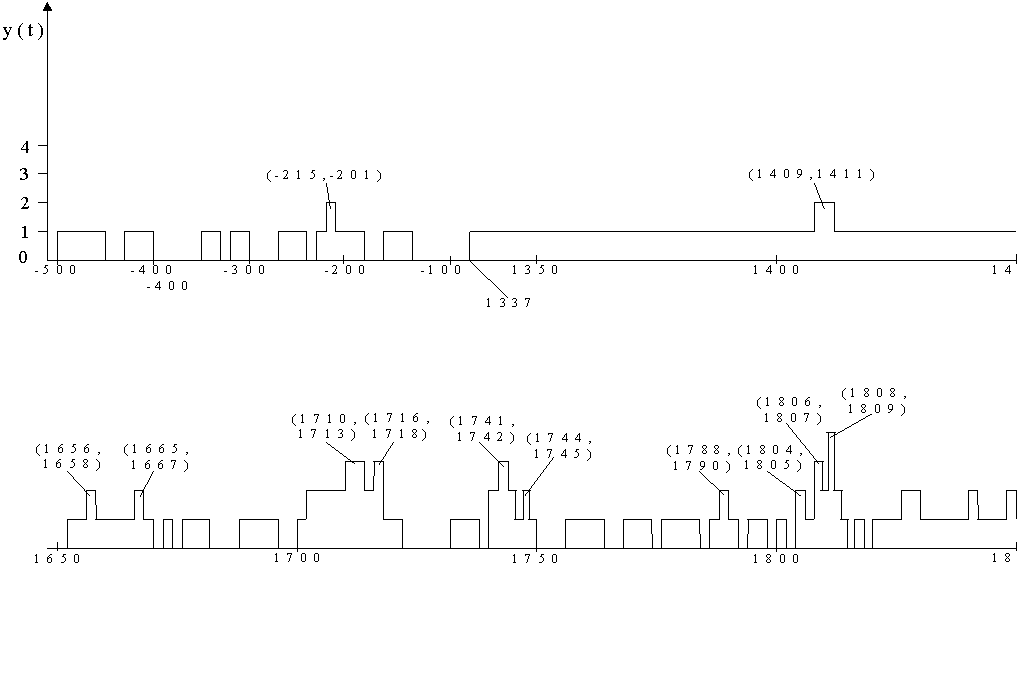
Рис. 3. Плотность изучаемого суммарного потока войн. Высота любого импульса процесса в произвольный момент показывает число одновременно происходящих в этот момент войн, а его ширина – время, в течение которого происходит данное число войн. Особо (в скобках) показаны интервалы времени, в которых происходит рекордное число войн. Например, видим, что на интервале времени происходит одна война, однако на малом его подынтервале происходят одновременно две войны.

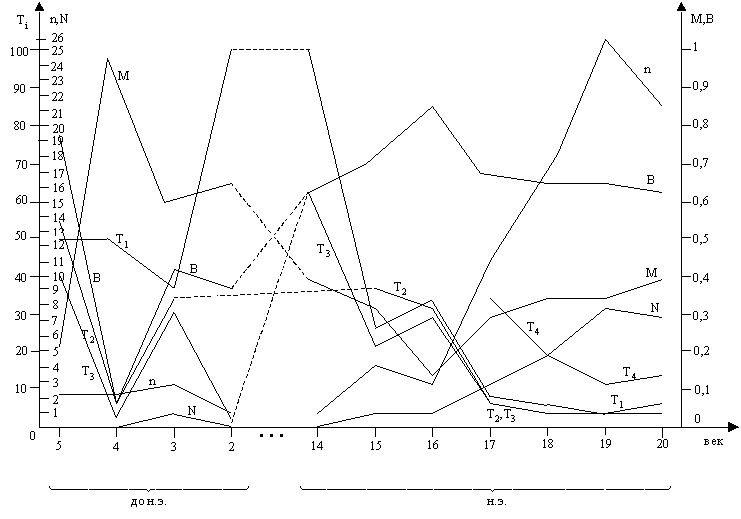
Рис.4. Графики количественных характеристик (названия характеристик см. в табл. 4).

AUTOMATON MODELING OF WARS

V. I. Levin

Designed strategy of calculation of quantitative features of sequences of wars with use end dynamic automaton models. With its help executed calculation of features and analysis of sequence the most to famous for last 2500 years of wars.