Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 18. -

Вып. 1. - 2019. - URL:

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/TITL.HTM

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-61-html/TITL-61.htm

http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-61-html/cont.htm

УДК 539.194:541.8

ФИЗИКА АНОМАЛИЙ ВОДЫ БИОЛОГИЧЕСКИХ СИСТЕМ

© 2019 г. Холманский А. С.

(kholmanskiy.docx) (kholmanskiy.pdf)

Аномальные температурные зависимости (ТЗ) свойств жидкой воды биологических систем аппроксимировали функциями вида f_a=Т^±βexp(±E_a/RT). Знаки и величины β подобрали для каждой характеристики с учетом формул Дебая и Стокса, а тепловые эффекты (E_a) на температурных интервалах между экстремальными точками определили с помощью уравнения Аррениуса. Реакции перестройки структуры воды, ответственные за аномалии ТЗ характеристик, подразделили на экзо и эндотермические, а сами характеристики на динамические и условно статические. Величины E_a для первых коррелировали с энергий водородной связи и мало менялись в присутствии NaCl (0.5 моль/л). Для статических характеристик величины E_a были одного порядка с энергиями трансляционных и крутильных движений молекул. Возрастание E_a динамических характеристик при температурах ниже 25^оС связали с увеличением доли гексагональных льдоподобных кластеров в надмолекулярной структуре воды. Температуры экстремумов ТЗ статических характеристик следовали из решения уравнения дf_a/дT=0 и их значения были пропорциональны величинам E_a соответствующих аппроксимаций.

Ключевые слова: свойства воды, аномалии, температурные зависимости, экстремумы, водородная связь, колебания, перестройка структуры.

ВВЕДЕНИЕ

Благодаря аномальным физико-химическим свойствам жидкой воды на Земле возникла жизнь во всем своем многообразии. Термодинамические свойства морской воды и воды биологических систем в процессе эволюции обеспечили развитие механизмов адаптации живых организмов к воздействиям глобальных и переменных геокосмофизических факторов. Аномалии жидкой воды при нормальном давлении проявляются, прежде всего, на температурных зависимостях (ТЗ) ее характеристик в широком диапазоне реальных температур (-30-100^оС). Для биогенеза большое значение имеют также аномальные свойства охлажденной и переохлажденной воды, сохраняющей жидкое состояние в водных дисперсиях и биоорганических системах при 30<t<10^оС [1, 2].

ТЗ плотности (ρ), изобарной теплоемкости (С_р), изотермической сжимаемости (γ) и скорости звука (V) при t>0^оС имеют экстремумы в окрестностях точек (t_Э) 4; 36; 46; 75^оС, соответственно. В этот ряд помимо точки кристаллизации воды 0^оС включилиточку25^оС, учитывая, что в окрестности 25^оС меняются ТЗ ряда характеристик воды [3, 4]. Кроме того, зависимости сдвиговой вязкости (η_s) и коэффициента самодиффузии (D) от давления при t25^оСимеют экстремумы при ~1кбар [5-7]. При t< 25^оС наблюдается увеличение удельной оптической активности ([α]) растворов сахаров [8]. ТЗ инфракрасных и рентгеновских спектров жидкой воды[5, 9] указывают на присутствие в ней при t<40^оС льдоподобных гексагональных кластеров в составе сетки из тетраэдрических водородных связей (Н-связей)[5, 7].

Физическая природа аномалий жидкой воды и экстремумов ТЗ ее характеристик до сих пор не установлена, не смотря на огромное количество разного рода исследований воды в рамках законов термодинамики. По-видимому, для понимания природы аномалий воды и механизмов влияния на водосодержащие биосистемы внешних физических факторов следует учитывать квантовые правила отбора, а также нелинейные, кооперативные и резонансные эффекты [9, 10]. К примеру, правила отбора в переходах между спиновыми состояниями молекул воды отвечают за особенности реологии крови в окрестностях t_Э~36.6^оСианомалии ТЗ [α] водных растворов сахаров [8]. При этом энергии основных состояний и переходов между орто- и параизомерами воды коррелирует с величинами энергией активации (Е_а) температурных зависимостей [α].

Явление резонанса может быть также ответственно за аномалии ТЗ свойств воды в окрестностях точки 25^оС. В работе [11] получена формула для частоты когерентных колебаний z протонов в спиральной цепочке тетраэдрических Н-связей:

. (TГц)

Из этой формулы для z= 12 получается ν_z= 6,08 ТHz и энергия колебаний ~2,4 кДж/моль, которой соответствует тепловая энергия при T = 298К (~25^оС).Поскольку в льдоподобном гексагональном кластере содержится 12 протонов, то можно предположить, что в воде в окрестностях точки 25^оС по резонансному механизму происходит перестройка гексагонального кластера в спиральную цепочку из 6 молекул воды. При этом снижается η_s и возрастает D.По-видимому, такой же эффект на структуру воды оказывает высокое давление при t25^оС.

Учитывая различные теоретические модели структуры и динамики жидкой воды, в работе [3, 4] предположили, что в точках t_Э происходят перестройки и расслоения надмолекулярной структуры воды на динамичные квазифазы, различающиеся уровнем и типом кластеризации молекул. Именно такие надмолекулярные структуры могут обладать кооперативными свойствами и обеспечивать высокую чувствительность водосодержащих биосистем к внешним факторам различной природы. Представляет интерес вопрос об особенностях аномалий морской воды и водных дисперсий [1].

В результате перестройки динамичной структуры воды меняется энергетическое состояние отдельной молекулы, перераспределяются водородные связи и в результате этого межмолекулярные связи могут усиливаться или ослабевать. Перестройки происходят на микро и макроуровнях, охватывая коррелированные состояния, как отдельных молекул, так и различных кластерных образований. Можно предположить, что физика аномалий ТЗ каждой характеристики воды связана с определенным типом молекулярной динамики, включающей обратимые реакции разрыва Н-связи, трансляционные, вращательно-колебательные и спин-спиновые переходы.

В рамках законов равновесной термодинамики всем этим реакциям и переходам будет соответствовать свои значения теплового эффекта (ΔQ) и энергии активации (Е) (Рис. 1). Эти величины входят в уравнения Аррениуса и Вант-Гоффа и определяют кинетику равновесных процессов перестройки структуры воды, отвечающих за аномалии ТЗ характеристик воды.

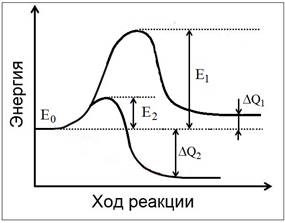
Рис. 1. Энергетические профили эндо- (1) и экзотермической (2) реакций перестройки структуры воды. Е – барьеры реакции (энергии активации); ΔQ – тепловые эффекты.

Зависимость кинетики перестройки от Т формально выражается через ТЗ константы равновесия (К_р) или через ТЗотношения констант скоростей прямой (К₁) и обратной (К_-1) реакций, доминирующих в каждом типе перестройки структуры. Таким образом, основу физически адекватной аппроксимации ТЗ характеристики воды должна составлять функция Т вида:

.(1)

В (1) предэкспонента А обычно не зависит от Т, а величина ΔQ меняется в диапазоне от энергии кванта вращательного перехода до энергии разрыва Н-связей. В эмпирических аппроксимациях ТЗ характеристик воды ΔQ фигурирует как эффективная энергия активации, поэтому в дальнейшем сохранили для нее традиционное обозначение Е_а или Е.

В работах, посвященных исследованиям физики воды, применяют в качестве аппроксимаций ТЗ ее характеристик различные комбинации функции типа f_a, в которых предэкспонента А может быть степенной функцией Т. Типичные примеры f_a для динамических характеристик воды:

, (2)

[12];

[13];

[12];

; [3, 4].

Здесь R – газовая постоянная (8.3 Дж·моль^-1·К^-1), С_i, – константы; Е_а, Е_{i –} эффективные энергии активации; α – тангенс угла наклона соответствующих анаморфоз [3, 4].

Применимость функций f_a предполагает структурную однородность воды в макро масштабе:(2)– формула Френкеля для ТЗ динамической вязкости (η); f₁ получена с учетом двух льдоподобных кластеров, а f₂ учитывает различия динамики свободных молекул воды в кластерах, образующихся при низких (Е₁= 39.4) и высоких (Е₂=13.4 кДж/моль) Т. Функция f₃не адекватна по отношению к свойствам жидкой воды из-за величины Т_о~150К, которая находится вне диапазона реальных температур. В работе [3] f₄ применили для аппроксимаций ТЗ η, коэффициента самодиффузии (D) и времени диэлектрической релаксации (τ_D), а физически неадекватную функциюf₅– для аппроксимаций ТЗ ρ, V, C_Р и γ. В работах [3, 4] весь диапазон Т разбивали точками t_Э на Т-интервалы, на которых линейные аппроксимации имели разные величины Е_а.

Для выяснения особенностей молекулярной динамики, ответственных за аномалии свойств воды, солевых водных растворов и дисперсий в настоящей работе применили для аппроксимаций температурных зависимостей основных характеристик воды в диапазоне -30-100^оС физически адекватные функции и сопоставили эффективные энергии активации с известными энергиями атомно-молекулярных движений и процессов в жидкой воде.

МЕТОД И МАТЕРИАЛЫ

Эмпирические данные по ТЗ характеристик воды брали из справочников или из оригинальных работ, оцифровывая при необходимости графики с помощью компьютерной программы Paint. Границы всего диапазона ТЗ определялись исходными данными, которые менялись в пределах от -30 до 100^оС. Т-интервалы для аппроксимаций ТЗ характеристик воды с экстремумом обязательно имели одну разделительную точку, соответствующую экстремуму, которую в ряде случаев дополняли значениями t_Э для других ТЗ. Для большинства характеристик воды в качестве t_Э брали 25^оС, что отвечало универсальности процесса образования надмолекулярной динамической структуры из гексагональных льдоподобных элементов в Т-интервале 0-25^оС. Места стыковок смежных Т-интервалов на графиках аппроксимаций отмечали стрелками. Для построения аппроксимаций ТЗ использовали программу Excel. Критерием достоверности аппроксимаций на различных Т-интервалах служила степень близости величины R² к 1. Физическую адекватность вида f_a определяли путем согласования знака экспоненты и величины показателя степени Т^±β в предэкспоненте с известными соотношениями между характеристиками воды. При этом оптимальное значение β выбирали из ряда 0, ±1/2, ±3/2, ±2.

Вид функций f_a для D и η согласовали с функций f_η и формулой Стокса-Эйнштейна:

,

в которой k – постоянная Больцмана, a – радиус частицы. При выборе функций f_a для времени спин-решеточной релаксации (Т₁) учли пропорциональность Т₁ коэффициенту самодиффузии D [13], а для времени спин-спиновой релаксации (Т₂) и τ_D их пропорциональность времени вращательной релаксации (τ_r), которое выражается формулой Дебая [13]:

.

Вид выбранных функций f_a для γ, V и ρ удовлетворял известному соотношению:

V = (γ ρ)^-1/2.

РЕЗУЛЬТАТЫ

Графики аппроксимаций и исходных литературных данных представлены на рисунках 1-13, а вид функций f_a и величины Е_а, приведены в Таблице и на Рис. 13.

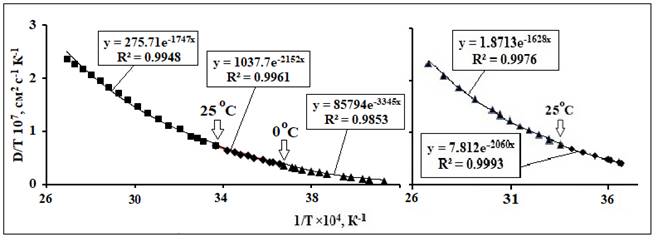
Рис. 2. f_a-Аппроксимации ТЗ коэффициента самодиффузии Н₂¹⁷О (D). Значения D(t) для(а) и ( b)взяты из работ [13, 14], соответственно.

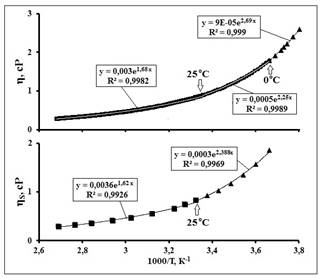
Рис. 3. f_a-Аппроксимации ТЗ динамической (η) и сдвиговой вязкости воды (η_s). Данные по η(Т) и η_s(Т) взяты из [15, 16], соответственно. Линии трендов бесцветны и прерывисты.

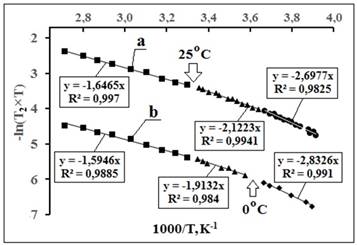
Рис. 4. f_a-Аппроксимации ТЗ времени релаксации спинов протонов (Т₂) дистиллированной воды (а), водный раствор NaCl (0.5 М) (b), исходные данные из [12].

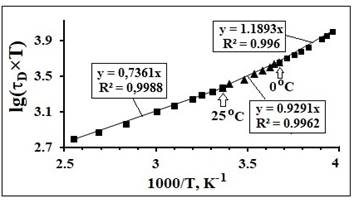
Рис. 5. f_a-Аппроксимации ТЗ времени диэлектрической релаксации (τ_D), исходные данные из [17].

Рис. 6. Аппроксимации экспериментальной ТЗ времени спин-решеточной релаксации (Т₁): а) – суммой двух экспонент (С₁ и С₂ – константы) [13] и b) – f_a-аппроксимации.

Рис. 7. Температурная зависимость теплоемкости воды (С_р) от Т (а) и ее f_a-аппроксимации(b). для Т>273 К из [17], а для Т<273 К получены оцифровыванием графика С_р(Т) из [18]. Линии трендов бесцветны.

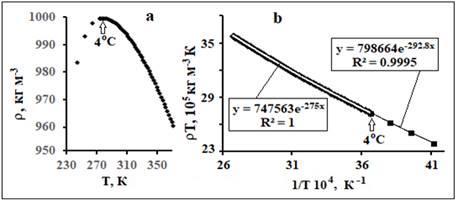
Рис. 8. Температурная зависимость плотности воды (ρ) от Т (а) и ее f_a-аппроксимации(b). Данные по ρ (Т) для Т>273 К из [15], а для Т<273К получены из графика ρ(Т) из [18].

Рис. 9. Зависимость скорости звука в воде (V) от Т (a) и ее аппроксимации(b). Данные по V(T) взяты из [19]. Стрелками показаны границы интервалов(в ^оС). Линии трендов бесцветны.

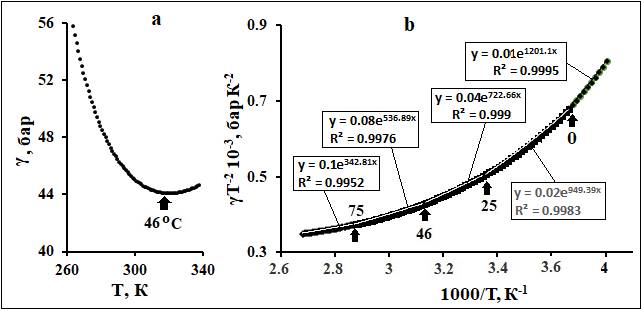
Рис. 10. Зависимость сжимаемости воды (γ) от Т (a) и ее f_a-аппроксимации(b). Данные по γ (T) взяты из [20]. Стрелками показаны границы интервалов (в ^оС). Линии трендов бесцветны.

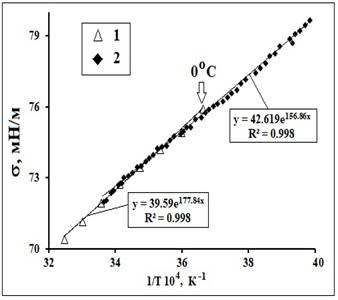
Рис. 11. Аппроксимации ТЗ коэффициента поверхностного натяжения (σ). Данные по σ (t) взяты из [21] (1) и из[18] (2).

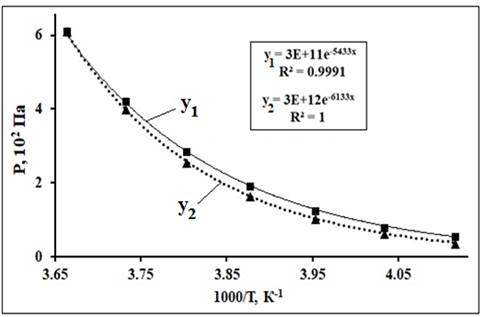
Рис 12. Аппроксимации ТЗ давления насыщенных паров над переохлажденной водой (у₁) и льдом (у₂). Данные по Р(Т) из [22].

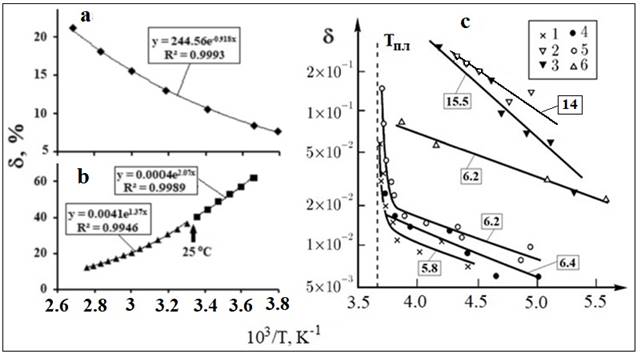
Рис. 13. f_a-Аппроксимации ТЗ доли (δ) свободных молекул воды (а) и молекул с водородными связями (b). Зависимость относительного содержания подвижной фазы воды (δ) от 1/Т (с) – раствор белка (1), адсорбционные пленки воды на аэросиле (2), на силикагеле (3) и водных дисперсий Na-монтмориллонита (4), аэросила (5), Са-каолинита (6); Т_пл= 0^оС,вквадратных рамках Е_а(кДж/моль).Исходные данные для (а), (b), (с) взяты из [5, 23, 1], соответственно.

Таблица

Экстремальные точки, вид функций f_a и энергии активации температурных зависимостей характеристик воды

N	Характеристика воды		fa	tЭ(^оС)	Интервал ∆t (^оС)	Еа (кДж/Моль)
1	Коэффициент самодиффузии, данные из [13, 14] (D, cm^2 c^-1)		Техр(-Еа/RT)	0; 25	-23 – 0	27.8
					0 – 25	17.9 (17.1)
					26-100	14.5 (13.5)
2	Время спин-решеточной релаксации (Т1, с)		Техр(-Еа/RT)	0; 25	-20 – 0	28.9
					5 – 25	19.2
					30 - 100	13.1
3	Динамическая вязкость (η, спз)		ехр(Еа/RT)	0; 25	–10 – 0	22.4
					0 – 25	18.6
					25 – 100	14.0
4	Сдвиговая вязкость (ηs, спз)		ехр(Еа/RT)	0; 25	0 – 28	19.8
					28 – 100	13.5
5	Время диэлектрической релаксации (τD, с)		Т^-1ехр(Еа/RT)	0; 25	-20 – 0	22.7
					0 – 25	17.8
					25 – 100	14.0
6	Время спин-спиновой релаксации протонов воды (раствор NaCl 0.5 М) (Т2, с^-1)		Т^-1ехр(Еа/RT)	0; 25	-20 – 0	22.4 (23.5)
					~0 - 25	17.6 (15.9)
					30 - 100	13.7 (13.2)
7	Изобарная теплоемкость (Ср, Дж г^-1 K^-1)		Техр(Еа/RT)	35	-27 – 0	4.5
					0 – 35	2.6
					35 – 100	2.7
8	Плотность (ρ, кг м^-3)		Т^-1ехр(-Еа/RT)	4	-30 – 4	2.4
					4 – 100	2.3
9	Скорость звука (V, м с^-1)		Т^-1/2eхр(-Еа/RT)	75	0-25	2.9
					26-46	2.3
					47-75	1.8
					76-100	1.1
10	Изотермическая сжимаемость (γ, бар^-1)		Т^2ехр(Еа/RT)	46	-10 – 0	10
					0 – 25	7.9
					25 – 46	6
					47 – 75	4.5
					76-100	2.8
11	Поверхностное натяжение (σ, мН/м)		ехр(Еа/RT)	25	-22 – 25	1.3
					0 – 35	1.5
12	Давление насыщенного пара над водой (льдом) (Р, Па)		eхр(-Еа/RT)	-	-30 – 0	45.1 (50.9)
13	Доля молекул (δ)	Свободных	eхр(-Еа/RT)	-	-9-100	7.6
		Связанных	eхр(Еа/RT)	25	0-25	17.2
					30-90	11.4

ОБСУЖДЕНИЕ

Существенное различие величин Е_а для всех характеристик воды позволяет подразделить их на динамические (δ, Р, D, η, τ_D,, Т₁, Т₂) и условно статические (С_р, ρ, V, γ, σ). Реакции, ответственные за аномалии ТЗ характеристик D, Т₁, V, Р и δ являются эндотермическими, а η, τ_D, Т₂, С_р, γ, σ экзотермическими. В первом случае связи между молекулами ослабляются в результате перестройки, а во втором – усиливаются. Порядок значений Е_а динамических характеристик согласуется с величинами энергией Н-связи (8-25 кДж/моль [5]) и между собой в соответствующих Т-интервалах. Отсюда следует, что в перестройках структуры воды, отвечающих за аномалии ТЗ динамичных характеристик, доминирует реакция разрыва Н-связи, кинетика которой не имеет выраженных экстремальных точек на их ТЗ. Соответственно, производные f_a-функций по Т для этих характеристик не обращаются в ноль во всех Т-интервалах.

Значения Еа меняются скачком для всех динамических характеристик в точке25 °С, что коррелирует с резким ростом роли льдоподобных гексагональных кластеров в молекулярной динамике, ответственной за TD соответствующих характеристик при t < 25 °С. Среднее арифметическое значение разности Е_а для Т-интервалов в диапазонах от 0 °С до 25 °С и от 25 °С до 100 °С равно5,4 ± 10% кДж/моль для всех эндо- и экзотермических реакций структурных переcтроек воды. Это значение хорошо коррелирует со значением удельной теплоты кристаллизации для воды и удельной теплоты плавления для льда(6 кДж / моль), а также с разницей между значениями Е_а реакции испарения переохлажденной воды и льда, т. е. 5,8 кДж/моль (см.Таблицу). Таким образом, перестройку гексагональных льдоподобных кластеров с тетраэдрическими Н-связями в интервале от 0 до 25 °С до определенной степени можно рассматривать как продолжение процессов плавления и кристаллизации Ih-льда.

Значения Е_а для статических характеристик близки к энергиям трансляционных и крутильных движений молекул, лежащими в областях 0.2-1 и 2.4-7.2 кДж/моль [24]. Из формулы (2) при подстановке в нее соответствующих f_a следует соотношение , которое хорошо выполняется в диапазоне 0-75^оС (см. Таблицу). Для статистических характеристик с экстремальными ТЗ, производные их f_а-функций обращаются в ноль в Т_Э. При этом для ρ, С_р,γ и V получаются следующие формулы для T_Э:

; ; .

Если взять из таблицы для ρ и С_р значения Е_а 2.3 и 2.6 кДж/моль, то величины Т_Э (t_Э) составят 277К (4^оС) и 313К (40^оС), соответственно. При подстановке в уравнения для γ и V значение Е_а, равное средней величине в интервалах, примыкающих к 46 ^оС и 75^оС (6+4.5)/2 и (1.8+1.1)/2 кДж/моль, получим Т_Э (t_Э) – 319 К (46^оС) и 349К (76^оС), соответственно. Эти результаты свидетельствует о физической адекватности выбранных функций f_а для статических характеристик воды, имеющих экстремальные точки на ТЗ.

Для статических характеристик знак теплового эффекта будет зависеть от заселенности и энергии переходов между вращательно-колебательными и спиновыми состояниями молекул воды, а также от изменения степени кластеризации ее структуры. Последний фактор определяется величиной и знаком изменения энтропии реакции (ΔS). Величина энтропийного вклада в тепловой эффект (ТΔS) в случае экзотермических реакций перестройки надмолекулярных структур воды будет возрастать при понижении Т (см. Е_а для С_р, V, γ). Значение предельной величины |ТΔS| в экзотермических реакциях перестройки структуры не должно превышать теплового эффекта реакции кристаллизации 1 г воды (~0.055 Моль) при 0^оС, равного 0.33 кДж/моль. При перестройках в окрестностях t_Э и в переохлажденной области вода сохраняет свое жидкое состояние, это указывает на низкую энергию связи молекул в кластерах. Следовательно, значение |TΔQ|<0.33 кДж/моль, что существенно меньше Е_а даже для статических характеристик воды при Т>0^оС.

Учитывая условную аддитивность механизмов структурных перестроек, их представили кинетической схемой [4]:

На схеме А – сетка водородных связей, состоящая из n штук льдоподобных гексагональных кластеров (Н₂О)₆; В – надмолекулярные структуры из m однородных элементов, образованных из кластеров с g = 2, 3, 4, 5. Звездочкой помечены константы скорости вращательных переходов, подчиняющихся спиновым правилам отбора [6]. N обозначает молекулы, включенные в состав кластеров, а также молекулы участвующие в процессах самодиффузии. Данные молекулы можно считать «виртуально» свободными от Н-связей на время их «захвата» кластером или «прыжка» [3].

Для каждой Т в замкнутой системе устанавливается термодинамическое равновесие со своим набором кластеров и значения числа N. Из опыта следует, что при приближении температуры воды к 100^оСn в А стремится к 0; m в В стремится к 1 и g не превышает 2 (димеры), а доля N достигает ~20%. C учетом этих данных и времен жизни Н-связи в работе [4] приняли, что; ; и . При таких допущениях из условия термостационарного равновесия следуют соотношения:

k₁ = k₂и .

Комбинациями констант скоростей на схеме (3) определяются значения К₁ и К_-1 в (1), а значит, и вид f_а-функций для реакций, доминирующих в перестройках структуры воды. При этом величина и знак Е_а (ΔQ) зависят от числа и энергии Н-связей разрываемых и образующихся в прямой и обратной реакции. Для динамических характеристик средняя разница между этими числами для прямой и обратной реакции будет варьироваться от ~1 до ~3 в зависимости от характеристики воды и Т-интервала. В случае статических характеристик изменения трансляционно-крутильных состояний молекул будут происходить с сохранением числа Н-связей в кластерах или при их изоэнергетических трансформациях в прямых и обратных реакциях.

Зависимость предэкспоненты f_а-функций от Т^±βможет быть обусловлена следующими факторами. Молекулярные механизмы перестроек структуры воды включают трансляционную составляющую и поэтому зависят от распределения скоростей Максвелла, в предэкспоненту которого входит Т^–3/2.Крутильныеколебания и разрывы Н-связей сопряжены с изменениями квантовых состояний ОН связей [25], частота перехода между которыми подчиняется распределению Больцмана, содержащему в предэкспоненте Т [26].Для бимолекулярных реакций предэкспонента в формуле Аррениуса, характеризует частоту столкновений реагентов и пропорциональна Т^1/2 [26].Таким образом, вариации вида К₁ и К_-1 в (1) вполне могут обеспечить значения n в выбранных f_а-функциях.

Измерения σ в диапазоне от –22 до 27°С проведены путем визуального наблюдения за мениском в капилляре [18]. Эффектом капилляра можно объяснить различия в величинах Е_а для σ в Т-интервале 0 – 25°С (Таблица). Доля молекул воды, взаимодействующих со стенками капилляра по порядку величины сравнима с общим числом молекул. Эффект стенки может существенно влиять на термодинамику воды в гигроскопичных пещеристых средах верхних слоев литосферы.

Величины Е_а для динамичных характеристик при Т< 0^оС(переохлажденная вода)четко подразделяются на два ряда в соответствие с формулами Стокса-Эйнштейна (η, τ_D, Т₂) и Дебая(D, Т₁). В остальных Т-интервалах существенной разницы между величинами этих рядов не наблюдается (см. Таблицу).При равном количестве молекул воды и NaCl величина Е_а для Т₂ на 5% возрастает при t<0^oC, на 8.5% снижается в интервале 0 – 25 ^oC и далее не отличается от средней Е_а для всех динамических характеристик. Это согласуется с тем, что вращательная подвижность молекул воды в гидратных оболочках незначительно растет лишь в интервале 0 – 25 ^oC. Этот результат, по-видимому, обусловлен ускорением распада льдоподобных кластеров воды в присутствии ионов NaиCl.

Оценку доли свободной воды δ(t) в переохлажденном состоянии проводили при помощи ИК-спектроскопии по частоте ОН группы свободной воды [23], а долю незамерзшей воды в водных дисперсиях и в приповерхностном слое определяли по интенсивности узкой линии ЯМР. Установили, что количество связанной воды коррелирует с числом полярных групп на граничащих с водой поверхностях [1] и, по-видимому, из-за этого величины Е_а были вдвое больше для пленок воды, адсорбированных на гидрофильных поверхностях, чем для водной дисперсии родственных веществ (Рис. 13). В переохлажденных дисперсиях белка и гидрофильных веществ величина Е_а реакции «освобождения» молекулы воды оказалась одного порядка с теплотой плавления льда (см. Рис. 13, Таблицу).

ЗАКЛЮЧЕНИЕ

Результаты работы показали, что физически адекватные и достоверные аппроксимации аномальных температурных зависимостей характеристик жидкой воды в диапазоне -30 – 100^оСможно построить на основе формализма законов термодинамики и учета известных соотношений между характеристиками воды. Параметры аппроксимирующих функций определяются физической природой реакций перестройки структуры воды, отвечающих в основном за молекулярный механизм аномалий свойств воды. Установлено, что для динамических характеристик такими реакциями являются экзо и эндотермические перегруппировки кластерных структур с разрывом и перестройкой сетки водородных связей. Энергия этих связей и тепловой эффект реакции перестройки увеличиваются при температурах ниже 25^оСиз-за возрастания концентрации гексагональных льдоподобных кластеров. Для статических характеристик экзо и эндотермические реакции ограничены возбуждением трансляционных и крутильных колебаний молекул в рамках изоэнергетических трансформаций сетки из Н-связей. Величины RT_Э для этих характеристик пропорциональны тепловому эффекту доминирующей реакции перестройки структуры воды в соответствующей экстремальной точке. Энергия активации вращательных движений молекул воды слабо зависит от присутствия в ней электролита (NaCl). Термодинамику переохлажденных водных дисперсий белка и гидрофильных веществ лимитирует реакция родственная процессу таяния льда.

ЛИТЕРАТУРА

1. Аксенов С.И. Вода и ее роль в регуляции биологических процессов. М.: 2004. 212 с.

2. Холманский А.С., Ситанская И.Ю., Зайцева Н.В. Проявление аномальных физических свойств воды в физиологии семян // Вестник МГОУ. Серия: Естественные науки. 2015. №4. С.46-50.

3.Kholmanskiy A. Activation energy of water structural transitions // Journal of Molecular Structure. 2015. 1089. Р. 124.

4.Холманский А.С. Экстремальные точки температурных зависимостей свойств воды // Вестник РАСХН 2014. № 4. С. 7-11.

5. Eisenberg D., Kauzman W. The Structure and Properties of Water, 1969, 233с.

6. Сырников Ю.П. Вязкость. Физическая энциклопедия.URL: http://www.femto.com.ua/articles/part_1/0638.html.

7. Маленков Г.Г. Структура и динамика жидкой воды // Журнал структурной химии. 2006, 47, с. 5-35.

8. Kholmanskiy A. Chirality anomalies of water solutions of saccharides // Journal of Molecular Liquids. 2016. 216. Р. 683

9. Першин С.М. Физическая основа аномальных свойств воды - квантовые отличия орто и пара спиновых изомеров Н₂О // URL: http://www.biophys.ru/lib/sci/water/250-h2o-00029

10. Холманский А.С. Хиральность и квантовые эффекты как факторы морфогенеза // Математическая морфология: электронный математический и медико-биологический журнал.2010. Т. 9. Вып. 4. URL: http://www.sci.rostelecom67.ru/user/sgma/MMORPH/N-28-html/kholmanskiy-2/kholmanskiy-2.htm

11. Shimkevich 1, А., Shimkevich 2, I. On Water Density Fluctuations with Helices of Hydrogen

Bonds. Adv. in Condensed Matter Phys. 2011. Article ID 871231, DOI:

http://dx.doi.org/10.1155/2011/871231

12. Мельниченко Н.А. Структура и динамические свойства жидкой воды // Вестник ДВО РАН. 2010. № 1. С.65-74

13. Hindman J.C., Relaxation processes in water: Viscosity, selfdiffusion, and spinlattice relaxation. A. kinetic model // J. Phys. Chem. –1974. – 60, N 11. – P. 4488–4493

14. Holz М., Heila S. R., Saccob А. Temperature-dependent selfdiffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements // Phys. Chem. Chem. Phys., 2000, 2, Р. 4740–4742.10.

15. Справочник химика /под ред. Б.П. Никольского - М-Л.: Химия, 1982, т.1, стр. 547

16. Зацепина Г.Н. Свойства и структура воды, МГУ, 1974, 167 с.

17.Kaye G.W., Laby T.H. Tables of Physical and Chemical Constants. Longmans, 1970, 73 с.

18.Старостин Е.Г., Лебедев М.П. Свойства связанной воды в дисперсных породах. Часть I. вязкость, диэлектрическая проницаемость, плотность, теплоемкость, поверхностное натяжение// Криосфера Земли, 2014, т. XVIII, № 3, с. 46–54

19. Wagner W., Pruß A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use // J. Phys. Chem. Ref. Data, -31, -N. 2, 2002: http://www.nist.gov/data/PDFfiles/jpcrd617.pdf

20. Kell G. S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0" to 150°C: Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale Journal of Chemical and Engineering Data. 20(1), 1975. Р. .97-105

21. IAPWS Release on Surface Tension of Ordinary Water Substance //

http://www.iapws.org/relguide/surf.pdf

22. Анджелл К.А. Переохлажденная вода. Вода и водные растворы при температурах ниже 0 °С / Под ред. Ф. Франка. Киев, Наук. думка, 1985, с. 13–75.

23. LukeB, WaterPolym. 1984, 555 р.

24. Кизель В.А. Практическая молекулярная спектроскопия. М.: МФТИ, 1998. 256 с.

25. Ефимов Ю.Я. Асимметрия молекул Н₂О в жидкой фазе и ее следствия // Журнал структурной химии. -2001. -42, -№ 6 - .1122-1132

26. Шмид Р., Сапунов В. Н. Неформальная кинетика. В поисках путей химических реакций: М.: Мир, 1985. 264 с.

PHYSIC OF ANOMALIES OF WATER OF BIOLOGICAL SYSTEMS

Kholmanskiy A. S.

Anomalous temperature dependences (TD) of the properties of liquid water of biological systems were approximated by functions of the form f_a=Т^±βexp(±E_a/RT). Signs and values of β were selected for each characteristic, taking into account the Debye and Stokes formulas, and the thermal effects (E_a) on the temperature intervals between extreme points were determined using the Arrhenius equation. The water structure rearrangement reactions responsible for the anomalies of the TD characteristics were divided into exo and endothermic, and the characteristics themselves into dynamic and conditionally static. The values of E_a for the first ones correlated with the energies of the hydrogen bond and did not change much in the presence of NaCl (0.5 mol/l). For static characteristics, the values of E_a were of the same order as the energies of the translational and torsional motions of the molecules. The increase in E_a of the dynamic characteristics at temperatures below 25 °C was associated with an increase in the proportion of hexagonal ice-like clusters in the supramolecular structure of water. The temperatures of the extremums of the TD of the static characteristics followed from the solution of the equation дf_a/дT=0and their values were proportional to the values of E_a of the corresponding approximations.

Keywords: water properties, anomalies, temperature dependences, extremes, hydrogen bond, vibrations, structural rearrangement.

Научный центр «Бэмком»

г. Москва

Science Center «Bemcom», Moscow

Поступила в редакцию 27.01.2019