УДК 51
Лекция
АКСИОМАТИЧЕСКИЕ ТЕОРИИ
© 2000 г. Е. П. Емельченков, В.
Е. Емельченков
Рассматривается аксиоматический метод
построения математических теорий. Обсуждаются
свойства непротиворечивости и полноты
аксиоматических теорий.
Греки превратили математику в логическую систему, в которой от исходных предположений с помощью логического вывода, называемого доказательством, можно переходить к заключениям. В математике ничего не требуется принимать на веру. Математик ничего не рассказывает нам о реальности. Он говорит лишь о том, что одно следует из другого, и показывает, как именно это происходит. В истинности логических построений математика каждый может убедиться своим собственным разумом.
Ганс Фрейденталь
Математика в науке и вокруг нас
Одной из замечательных особенностей математических исследований двадцатого столетия является чрезвычайно широкое использование аксиоматического метода. Можно сказать, что математическая наука достигает совершенства лишь тогда, когда она принимает характер аксиоматической теории.
В данной лекции рассматривается
аксиоматический или дедуктивный метод
построения математических теорий. Материал
излагается на неформальном (содержательном)
уровне примерно в том объеме, в каком он
используется в повседневном математическом
обиходе.
1. Понятие аксиоматической теории
На уроке геометрии.
Учитель: "Для чего мы изучаем аксиомы?"
Ученик: "Чтобы их не доказывать".
Аксиоматический метод не является достижением только двадцатого столетия. В начале двадцатого века, благодаря главным образом работам немецкого математика Д. Гильберта (1862-1943), окончательно сформировались принципиальные положения данного метода, и было осознано его значение для математики. А первый шаг на этом пути был сделан более двух тысяч лет тому назад древнегреческим математиком Евклидом (около 300 г. до н. э.). Его труд "Начала" явился энциклопедией геометрических знаний и образцом написания математических работ на протяжении двадцати веков. Именно благодаря этому авторитетнейшему произведению сформировалось общечеловеческое представление об аксиоме как об утверждении, не требующем доказательства и являющем собой некую абсолютную истину.
В наше время в каждом среднем учебном заведении
изучается геометрия Евклида. Многие поколения
школьников на уроках геометрии знакомятся с
понятиями "аксиома", "теорема",
"доказательство", а также с образцами
безукоризненных логических рассуждений. На
пороге третьего тысячелетия очень трудно найти
людей, не имеющих представления о системе
Евклида. Они настолько редки, что после их
обнаружения об этом сразу же сообщают по
телевидению в рекламных роликах.
Параллельные линии не пересекаются, - доказано Евклидом.
Надежная бытовая техника существует, - доказано Zanussi.
Телевизионная реклама. Сентябрь 2000 г.
Внутри математической науки общепринятый взгляд на аксиомы претерпел самые решительные изменения. Важным этапом в процессе эволюции этих взглядов явилось построение во второй половине XIX века различных моделей неевклидовой геометрии. Оказалось, что терминам, входящим в аксиомы, и самим аксиомам можно придавать различный смысл, а не только тот наглядный, который имел в виду Евклид.
При аксиоматическом построении математических теорий обычно считается, что правила логики нам известны, и мы умеем интуитивно пользоваться ими. Аксиоматические теории, в которых правила логики явно не заданы, называются неформальными или интуитивными. При построении некоторой интуитивной аксиоматической теории придерживаются следующих этапов:
1) Задается некоторое множество понятий (терминов) называемых первичными или основными.
По сути дела на этом этапе выделяется одно или несколько множеств объектов теории и соответствий между ними. Например, приводя описание геометрии, Евклид рассматривал в качестве первичных понятия "точка", "прямая" и "лежать на". Последнее из понятий характеризовало некоторое соответствие между точками и прямыми.
В свое время Евклид сделал попытку строго
определить все первичные понятия геометрии
(точку, прямую, плоскость и т. д.). Ясно, однако,
что эти понятия должны определяться через
какие-то другие, те, в свою очередь, сами должны
определяться через какие-то понятия, и так далее.
Поэтому некоторые понятия приходится считать
первичными и не давать им никаких определений.
Все свойства первичных понятий, которыми можно
пользоваться в аксиоматической теории,
описываются в аксиомах.
Точка есть то, часть чего есть ничто.
Определение точки по Евклиду
Точка есть то, что под этим понимает каждый не
испорченный образованием человек.
Современное определение точки
Неопределяемость первичных понятий объясняется попросту тем, что попытка все определять приводит либо к регрессу в бесконечность; (процесс последовательных определений никогда не оканчивается), либо к порочному кругу (ситуация при которой в результате конечного числа последовательных шагов понятие определяется через само себя).
2) Выделяется некоторое подмножество высказываний о первичных понятиях. Эти высказывания называют аксиомами.
С аксиомами возникает ситуация аналогичная с утверждениями относительно первичных и определяемых понятий. Невозможно доказать все справедливые утверждения об этих понятиях. При доказательстве любого утверждения нужно опираться на какие-то предыдущие утверждения, при их доказательстве, в свою очередь, - на следующие, и так без конца. Поэтому и здесь необходимо выделить некоторые утверждения и объявить их справедливыми в данной теории. В качестве таких утверждений, принимаемых без доказательства, выбираются аксиомы.
Вопрос о том, какие утверждения о первичных понятиях выбираются в качестве аксиом, заслуживает специального рассмотрения. Отметим только, что Евклид в качестве пяти своих аксиом (постулатов) выбрал наиболее, на его взгляд, очевидные утверждения о точках и прямых.
3) При помощи первичных понятий даются определения всех остальных понятий.
Как отмечалось выше, первичные понятия аксиоматической теории не определяются. Вместе с тем, все другие понятия, которые предполагается использовать в теории, должны быть строго определены через первичные неопределяемые понятия и через понятия, смысл которых был определен раньше. Высказывание, определяющее таким способом значение понятия, называется определением, а само понятие, смысл которого определен, носит название определяемого понятия.
4) На основе аксиом и определений чисто логическим путем выводятся новые утверждения о первичных и определяемых понятиях. Получаемые новые утверждения называются теоремами данной аксиоматической теории.
Можно более точно сформулировать понятие
теоремы аксиоматической теории. Сначала, однако,
мы определим понятие доказательства. Доказательством
или выводом в аксиоматической теории T
называется конечная последовательность В1,
В2, ..., Вs высказываний теории, в
которой каждое высказывание является либо
аксиомой, либо получается из предыдущих
высказываний данной последовательности с
помощью логических правил вывода. Высказывание C
аксиоматической теории T, называется теоремой
теории T, если существует вывод, в котором
последним высказыванием является C. Тот факт,
что высказывание C является теоремой теории T,
обозначается символом С.
Отметим, что каждая аксиома аксиоматической теории является ее теоремой. Доказательством аксиомы является одноэлементная последовательность, состоящая из нее самой.
Важным является следующее обобщение понятия
теоремы. Пусть Г - конечное множество
высказываний некоторой аксиоматической теории.
Утверждение C теории называется выводимым
из Г (и обозначается Г C), если существует конечная
последовательность высказываний В1, В2,
..., Вs, называемая выводом C из Г,
каждое высказывание которой является либо
аксиомой, либо высказыванием из Г, либо
получено из одного или более предыдущих
высказываний этой последовательности по
какому-либо из правил вывода рассматриваемой
теории, а последнее высказывание Вs
есть утверждение С. Утверждения из Г
называются гипотезами (или посылками, или
допущениями). В частном случае, когда Г=O,
вывод C из Г превращается в
доказательство утверждения C, а C
становится теоремой аксиоматической теории.
Итак, под аксиоматической теорией, построенной на основе системы аксиом , понимается совокупность всех теорем, доказываемых, исходя из этой системы аксиом S. Такую совокупность теорем обозначают Th(S).
Изложенный метод построения математической
теории носит название аксиоматического или дедуктивного
метода. Выбор системы аксиом условен. Одно и то
же утверждение теории может быть аксиомой, если
оно так выбрано, а может выступать в качестве
теоремы, если выбор аксиом осуществлен по-иному.
Таким образом, если в обыденной жизни за термином
"аксиома" утвердился его изначальный смысл
(в переводе с греческого "аксиома" означает
"достойный признания"), именно смысл
самоочевидной, безусловной истины, то в
математике, при построении аксиоматических
теорий, аксиомы условны. Они "достойны
признания" не сами по себе, не ввиду их
самоочевидной истинности, а потому что на их
основе строится та или иная аксиоматическая
теория. При новом выборе системы аксиом прежние
аксиомы становятся теоремами. Коротко говоря,
аксиомы - это то, из чего выводятся теоремы, а
теоремы - то, что выводится из аксиом.
| Через точку A, не принадлежащую прямой
l, проходит единственная прямая параллельная l. Евклид Через точку A, не принадлежащую прямой l, проходит бесконечно много прямых параллельных l. Лобачевский, Больяи, Гаусс Через точку A, не принадлежащую прямой l, не проходит ни одной прямой параллельной l. Риман |
Не требуется "верить" аксиомам. Даже
поднимать этот вопрос и бесполезно и
бессмысленно. В старых школьных учебниках
геометрии бытовала фраза: "Справедливость
аксиом подтверждается многовековым опытом
человечества". Этот тезис с точки зрения
"чистого" математика не имеет никакого
смысла. В самом деле, как может "многовековой
опыт человечества" (или какие угодно иные
аргументы) подтвердить или опровергнуть тот
факт, что для любой прямой l и точки A
плоскости () в плоскости
существует единственная прямая, проходящая
через точку A и не пересекающая прямую l.
Данный факт представляет собой всего лишь
условное соглашение, и никакой проверке его
истинность не подлежит.
Для построения геометрии Евклид в качестве
одной из аксиом выбрал первое из перечисленных
предложений и развил на этой основе стройную
аксиоматическую теорию, названную впоследствии
евклидовой геометрией. Однако, если заменить
предложение Евклида на любое из двух других
предложений, можно построить другие не менее
стройные аксиоматические теории.
| Аксиомы - это как правила игры. Если их
изменить, вы будете играть уже в другую игру. Ян Стюарт |
2. Как возникают аксиоматические теории
Можно указать два пути, по которым происходило становление тех или иных аксиоматических теорий, известных в математике.
Первый путь состоит в том, что та или иная математическая теория, достигнув достаточно высокого уровня развития, принимает характер аксиоматической теории. Именно таким путем были аксиоматизированы такие математические теории, как арифметика, геометрия, теория вероятностей, механика и другие.
Второй путь возникновения аксиоматических
теорий состоит в том, что обнаруживалось
глубокое внутреннее сходство между основными
чертами, казалось бы, совершенно различных
математических теорий. Данное обстоятельство
наводило на мысль выделить общие черты и,
руководствуясь ими, построить аксиоматическую
теорию.
Математика - это искусство называть разные вещи одним и тем же именем.
Д. Гильберт
На этом пути возникли практически все
алгебраические аксиоматические теории (теории
групп, колец, полей, общая или универсальная
алгебра и другие). При таком подходе появляется
возможность взаимопроникновения методов одних
математических наук в другие, а также
возможность свободно интерпретировать
первоначальные понятия и аксиомы
аксиоматической теории. Последнее раскрывает
широкие перспективы для приложения таких теорий
и является одним из мощных источников
действенной силы математики как науки вообще.
3. Примеры аксиоматических теорий
Приведем два примера аксиоматических теорий.
Примр 3.1.Теория аффинных плоскостей. Первичными понятиями этой теории являются точка и прямая, характеризующие принадлежность объектов аксиоматической теории некоторым множествам (множеству точек и множеству прямых). Третьим первичным понятием теории является инцидентность, характеризующее определенное соответствие между точками и прямыми. Если точка A связана соответствием инцидентности с прямой a, то говорят, что точка A инцидентна прямой a, и пишут A I a.
Все свойства прямых, точек и отношения инцидентности описываются тремя аксиомами.
A1. Существуют три точки не инцидентные одной прямой.
A2. Любые две различные точки инцидентны единственной прямой.
Прежде чем сформулировать третью аксиому, введем определение.
Определение D1. Две прямые l и m, не
имеющие ни одной общей точки или полностью
совпадающие, называются параллельными
(обозначение: l m).
A3 (аксиома параллельных). Для любой
точки A и прямой l существует единственная
прямая m такая, что A I m и m l.
Поразительно, что такая бедная аксиоматика приводит к содержательной теории.
Пример 3.2. Теория эквивалентности. В качестве простого примера аксиоматической теории рассмотрим теорию, описывающую отношение эквивалентности. Эта теория имеет дело с одним типом объектов, множество которых будем обозначать буквой X. Для этих объектов не вводится специальное название (но можно было бы, конечно, назвать их как угодно). Объекты связаны единственным бинарным отношением . При этом требуется выполнение трех аксиом B1-B3.
B1. Отношение a
транзитивно, то есть для любых трех объектов из aa b
и bac следует aa c.
B2. Отношение a
симметрично, то есть для любых двух объектов из aa b
следует baa.
B3. Отношение a
рефлексивно, то есть для любого объекта выполняется условие aa a.
Для читателей, не знакомых с бинарными отношениями, ниже приводятся необходимые определения и примеры. Более подробное изложение вопросов, связанных с бинарными отношениями, можно найти в одной из предыдущих лекций [1].
Определение 3.1. Бинарным отношением на
множестве X называется любая совокупность
упорядоченных пар (x, y), где .
Например, пусть X = {a, b, c, d, e}. Тогда множество кортежей = {(a, b), (a, c), (b, d), (c, e), (e, e), (e, b)} является отношением на множестве X.
Обычно отношения задаются не перечислением элементов множества , а путем указания свойства пар (x, y), принадлежащих этому множеству. Например, отношение a = {(4, 4), (3, 3), (2, 2), (4, 2)} на множестве X = {4, 3, 2} можно определить как свойство "делится" на этом подмножестве целых чисел.
Хорошо известными примерами отношений из школьного курса математики являются:
Факт принадлежности кортежа (x, y)
отношению a, часто обозначают с
помощью так называемой инфиксной формы записи: xa y. Типичными примерами таких
записей из курса математики являются: x > y,
a = b, 8 4,
m l, a
b и т. п.
Широко распространен способ представления
отношений, основанный на использовании
ориентированных графов. При таком представлении
элементы множества X изображаются вершинами
графа (точками плоскости), а элементы (x, y)
отношения a дугами (стрелками),
соединяющими первую компоненту x отношения
со второй компонентой y. Граф бинарного
отношения a из приведенного выше
примера изображен на рисунке 3.1.
Рис. 3.1. Граф бинарного отношения на
множестве {a, b, c, d, e}
Очевидно, что произвольные бинарные отношения изучать в общем плане не особенно интересно, о них можно сказать очень мало. Однако, если отношения удовлетворяют некоторым дополнительным условиям, относительно них можно делать более содержательные утверждения. В аксиомах были перечислены три свойства бинарных отношений: транзитивность, рефлексивность и симметричность.
Примерами транзитивных отношений служат:
Отношение "быть похожим" на множестве людей не обладает свойством транзитивности.
Примерами симметричных отношений являются:
Отношение "x брат y" на множестве всех людей не является симметричным. В то же время отношение "x брат y" на множестве мужчин симметричным является.
В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x.
В графе рефлексивного отношения в каждой вершине графа обязательно имеется петля.
Определение 3.2. Бинарное отношение a на X называется антирефлексивным,
если ни для одного не
выполняется условие aaa.
Определение 3.3. Бинарное отношение a на множестве X называется антисимметричным,
если для любых различных элементов условия aab и baa не выполняются одновременно.
Например, отношение "делится" на множестве
натуральных чисел является антисимметричным,
так как из следует, что a = b.
Однако на множестве целых чисел отношение
"делится" антисимметричным не является, так
как
, но -2 2.
Отношения "выше", "тяжелее", "старше" антисимметричны на множестве людей. Отношение "быть сестрой" на множестве всех людей антисимметричным не является.
В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.
Определение 3.4. Бинарное отношение на множестве X называется связным, если для любых двух различных элементов a и b имеет место aab, либо baa.
Примером связного отношения является отношение "больше" на множестве действительных чисел. Отношение "делится" на множестве целых чисел связным не является.
4. Интерпретации и модели аксиоматической теории
Формулируя аксиомы в примерах предыдущего пункта, нами не учитывалась природа элементов тех множеств, которые там встречаются, а также природа других первоначальных понятий этих аксиоматических теорий.
Определение 4.1. Приписывание значений первичным понятиям аксиоматической теории называется интерпретацией теории. Если некоторая совокупность объектов и соответствий между ними, выбранных в качестве значений первоначальных понятий аксиоматической теории, то есть в качестве ее интерпретации, удовлетворяет всем аксиомам теории, то она называется моделью данной аксиоматической теории (или моделью системы аксиом теории).
Другими словами, интерпретация теории - просто отображение f, областью определения которого является множество Т первоначальных понятий этой теории. Если же образ f(T) удовлетворяет всем аксиомам теории, то это есть модель данной теории.
Так для теории эквивалентности ее моделями служат:
Множество людей, рассматриваемое вместе с отношением "быть похожими" является интерпретацией теории эквивалентности, но не является ее моделью, так как в ней не выполняется аксиома транзитивности B3.
Обычная евклидова плоскость (плоскость, которая изучается на уроках геометрии в школе) является моделью теории аффинных плоскостей.
Другая модель аффинной плоскости возникает, если:
Приведем еще одну модель аффинной плоскости,
состоящую из конечного числа объектов.
Рассмотрим граф, приведенный на рисунке 4.1.
Рис. 4.1. Модель аффинной плоскости
Вершины графа будем считать точками аффинной плоскости, ребра графа - прямыми. Точку M будем считать инцидентной прямой l, если вершина графа, соответствующая точке M, принадлежит ребру, соответствующему прямой l.
В последней несколько необычной модели пять прямых изображены прямолинейными отрезками, а шестая прямая CB - отрезком кривой. При этом прямая CB по определению параллельна прямой AD.
Существуют и другие модели приведенных теорий. В такой возможности по-разному интерпретировать аксиоматические теории заключена одна из причин обширных приложений этих теорий в других науках и в практике.
Определение 4.2. Две модели некоторой аксиоматической теории называются изоморфными, если между множествами основных объектов этих моделей можно установить взаимно однозначное отображение, сохраняющее основные соответствия.
Пусть, например, в одной из двух моделей
какое-либо основное соответствие имеет значение , а в другой
. Тогда, если объекты x1 и y1
первой модели связаны соответствием
, то соответствующие им
объекты x2 и y2 и второй модели
должны быть связаны соответствием
(и обратно):
.
Пример 4.1. Теория AT. Рассмотрим аксиоматическую теорию, в которой, подобно теории аффинных плоскостей, первичными понятиями служат: точка, прямая и инцидентность. За аксиомы примем следующие предложения:
C1. Любые две различные точки инцидентны хотя бы одной прямой.
C2. Любые две различные точки инцидентны не более чем одной прямой.
C3. Любой прямой инцидентны хотя бы две точки.
C4. Существуют три точки, не инцидентные одной прямой.
Рассмотрим некоторые модели теории AT.
Модель (а). Сопоставим первичным
понятиям теории конкретные термины модели в
соответствии с таблицей
Первичные понятия теории |
Термины модели |
| Точка | Шарик |
| Прямая | Стержень |
| Точка инцидентна прямой | Шарик надет на стержень |
На рисунке 4.2 представлена модель теории из
трех шариков и трех стержней.
Рис. 4.2. Модель (а)
Модель (б). Точки - стержни, прямые - шарики, смысл отношения инцидентности - прежний.
Модель (в). Точки - четыре вершины тетраэдра, прямые - шесть ребер тетраэдра, точка считается инцидентной прямой, если вершина является концом ребра. (Можно было принять за точки грани тетраэдра, а за прямые - его ребра).
Модель (г). Точки - числа 2, 3, 5, прямые - числа 6, 10, 15, точка A считается инцидентной прямой b, если b делится на A.
Модель (д). Точки - числа 1, 2, 3, прямые - числовые множества {1, 2}, {1, 3}, {2, 3}, инцидентность понимается как принадлежность в теоретико-множественном смысле.
Модель (е). Точки и прямые - это любые точки и прямые трехмерного евклидова пространства; инцидентность понимается также, как в евклидовой геометрии.
Модели (а) и (в) не изоморфны. Это следует из того, что между множествами первичных объектов моделей нельзя установить взаимно однозначное соответствие. По этой же причине не изоморфны модели (а) и (е).
Модели (а) и (г) изоморфны. Действительно, если установить взаимно однозначное соответствие следующим образом:
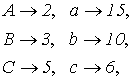
то оно будет сохранять инцидентность.
Аналогично доказывается изоморфизм моделей (а) и (б), а также (б) и (д).
Пример теории AT показывает, что использование аксиоматического метода позволяет установить связи между очень далекими, на первый взгляд, друг от друга областями. Вследствие существования различных моделей одной и той же системы аксиом, основанная на этой системе абстрактная теория может найти самые разнообразные применения.
5. Свойства аксиоматических теорий
Первый вопрос, который возникает, когда рассматривается та или иная аксиоматическая теория, - это вопрос о непротиворечивости, и полноте аксиоматической теории.
Непротиворечивость является важнейшим
требованием, предъявляемым к аксиоматическим
теориям.
Пословицы противоречат одна другой. В
этом собственно
и заключается народная мудрость.
С. Е. Лец
Определение 5.1. Аксиоматическая теория T
называется непротиворечивой, если для любого
утверждения A, сформулированного в терминах
этой теории, либо само утверждение A, либо его
отрицание недоказуемо
в этой теории T. Если для некоторого
утверждения A теории T оба утверждения
A и
доказуемы в T,
то аксиоматическая теория называется противоречивой.
Противоречивые модели математику не интересуют, поскольку в них чисто логическим путем можно доказать все, что угодно.
Когда однажды на обеде известный английский математик Дж. Харди сделал подобное замечание, кто-то из присутствующих потребовал обосновать его, доказав, например, из предположения 2 + 2 = 5, что некто Икс - папа римский. Харди ненадолго задумался и ответил: "Мы знаем также, что 2 + 2 = 4, значит 5 = 4. Вычитая 3, получаем 2 = 1. Икс и папа римский - это два человека, следовательно, господин Икс и папа римский - это один человек".
Таким образом, проблема установления
непротиворечивости аксиоматической теории
приобретает первостепенную важность. Для
неформальных аксиоматических теорий вопрос этот
во многих случаях удается решить с помощью
понятия модели. В самом деле, если теория
противоречива, то каждая ее модель содержит
противоречие, потому что пара противоречащих
друг другу теорем теории (A и ) переводятся в два противоречащих
друг другу высказывания о модели. Значит, теория
непротиворечива, если для нее удается указать
модель, свободную от противоречий.
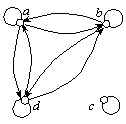
Рис. 5.1. Модель теории эквивалентности
Например, четырехэлементное множество X = {a, b, c, d} вместе с определенным на нем с помощью графа (рис. 5.1) бинарным отношением является, как можно убедиться самостоятельно, моделью теории эквивалентности. Поэтому с полной уверенностью можно утверждать, что аксиоматическая теория эквивалентности непротиворечива.
Для теории эквивалентности удалось построить конечную модель и тем самым решить вопрос о ее непротиворечивости. Но так бывает далеко не всегда. Может случиться, что аксиоматическая теория имеет только бесконечные модели. Тогда обоснование непротиворечивости теории сводится к доказательству отсутствия противоречий в модели, то есть по сути дела к доказательству непротиворечивости той аксиоматической теории, в терминах которой построена рассматриваемая модель. В этом случае доказательство непротиворечивости исходной теории приобретает относительную ценность: исходная теория непротиворечива, если непротиворечива теория, в терминах которой построена ее модель.
Именно такова ситуация с евклидовой геометрией. Непротиворечивость евклидовой геометрии никогда не была доказана, хотя почти все "уверены" в ее непротиворечивости. Доказательство ее относительной непротиворечивости может быть получено с помощью интерпретации, при которой точки интерпретируются посредством упорядоченных пар действительных чисел (x, y); а прямые - уравнениями первой степени ax + by + c = 0. Наличие модели построенной с помощью системы действительных чисел доказывает относительную непротиворечивость евклидовой геометрии: она непротиворечива, если непротиворечива теория действительных чисел. Но непротиворечивость теория действительных чисел также до сих пор не доказана. Путем построения соответствующих моделей вопрос о непротиворечивости теории действительных чисел может быть сведен к вопросу о непротиворечивости теории натуральных чисел или, как говорят к непротиворечивости арифметики.
В настоящее время непротиворечивость многих областей классической математики сведена к непротиворечивости арифметики. Тем не менее, "абсолютная" непротиворечивость ни евклидовой геометрии, ни теории действительных чисел, ни арифметики натуральных чисел не установлена. Уверенность в непротиворечивости этих теорий дает практика. Каждая из них позволяет делать выводы об окружающей материальной действительности, хорошо согласующиеся с нашим опытом. В этой адекватности отражения материального мира, в практической применимости и значимости указанных теорий и заключается главный критерий их непротиворечивости.
Упражнения
5.1. Докажите непротиворечивость аксиоматической теории порядка - теории с одним бинарным отношением, удовлетворяющим аксиомам транзитивности и антисимметричности.
5.2. Докажите непротиворечивость аксиоматической теории с одним бинарным отношением , удовлетворяющим аксиомам симметричности и антисимметричности.
5.3. Докажите непротиворечивость аксиоматической теории строгого линейного порядка - теории с одним бинарным отношением , удовлетворяющим аксиомам транзитивности, антисимметричности, антирефлексивности и связности.
5.4*. Докажите непротиворечивость аксиоматической теории проективных плоскостей. Эта теория имеет дело с двумя типами объектов - прямыми и точками. Объекты связаны единственным отношением I инцидентности точки A и прямой a (обозначение: A I a). Все свойства прямых, точек и отношения инцидентности описываются тремя аксиомами:
D1. Существуют три точки не инцидентные одной прямой.
D2. Любые две различные точки инцидентны точно одной прямой.
D3. Любым двум различным прямым инцидентна точно одна точка.
Обсудим теперь свойство полноты аксиоматических теорий. Можно сказать, что аксиоматическая теория называется полной, если она содержит достаточное для какой-нибудь цели количество теорем. В зависимости от целей различают несколько видов полноты. Мы ограничимся рассмотрением лишь одного из них.
Определение 5.2. Аксиоматическая теория
называется полной, если для любого
утверждения A, сформулированного в терминах
этой теории, по крайней мере, одно из утверждений A
или доказуемо в
этой теории.
Другими словами, аксиоматическая теория T является полной, если средств теории T достаточно для того, чтобы доказать или опровергнуть любое утверждение, сформулированное в терминах данной теории.
Теория, являющаяся одновременно
непротиворечивой и полной, является
максимальной в отношении непротиворечивости - в
том смысле, что добавление к такой теории T
в качестве аксиомы любого сформулированного в
терминах этой теории предложения, не являющегося
теоремой в T, приводит к противоречивой
теории. Действительно, если T -
непротиворечивая и полная теория и A -
недоказуемое в T предложение, то после
присоединения к T предложения A
получаем новую теорию T1, в которой
предложение A уже является теоремой. С другой
стороны, в силу полноты теории T из
недоказуемости предложения A следует
доказуемость . Таким
образом, в теории T1 доказуемы предложения
A и
, и,
следовательно, теория T1 противоречива.
Исследование аксиоматической теории на
полноту является непростой задачей. Однако,
иногда удается доказать неполноту теории, указав
конкретное предложение, недоказуемое и
неопровержимое в этой теории (предложение A
теории T называется неопровержимым,
если в T нельзя доказать предложение ).
Докажем, например, неполноту аксиоматической
теории эквивалентности T. Рассмотрим
предложение A, утверждающее связность
отношения . На рисунке 5.2 с помощью двух графов
заданы две модели теории эквивалентности.
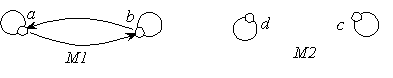
Рис. 5.2. Две модели теории
эквивалентности
В первой модели предложение A выполняется.
Следовательно, в теории T невозможно
доказать предложение .
Действительно, если бы в T предложение
было доказуемо, то это
предложение должно было бы выполняться для всех
интерпретаций T, в которых выполняются
аксиомы теории, т. е. для всех моделей теории T.
Так как в модели M1 предложение
не выполняется, то в T
невозможно доказать
.
Таким образом, A неопровержимо в T.
Во второй модели предложение A не выполняется. Поэтому в теории T предложение A недоказуемо.
Итак, мы указали конкретное предложение A теории T, которое недоказуемо и неопровержимо в T. Следовательно, теория T неполна.
Аналогично доказывается неполнота теории аффинных плоскостей. Рассмотрим, например, следующее предложение теории.
Предложение A. Пусть A, B, C - три точки
плоскости не инцидентные одной прямой. Через D
обозначим точку пересечения прямых l и m,
проходящих через точки A и C
соответственно, и таких, что m BA и l
BC (рис. 5.3). Тогда прямые AC и BC
пересекаются в единственной точке.
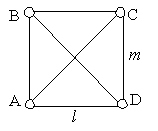
Рис. 5.3. Предложение A о пересечении
прямых
Выше мы рассмотрели две модели теории аффинных плоскостей: обычную евклидову плоскость и конечную четырехточечную аффинную плоскость (рис. 4.1). Из первой модели следует неопровержимость предложение A, а из второй - его недоказуемость. Следовательно, теория аффинных плоскостей неполна.
Заканчивая обсуждение свойства полноты
аксиоматических теорий, заметим, что многие
современные аксиоматические теории неполны.
Упражнения
5.5. Докажите неполноту аксиоматической теории порядка.
5.6. Докажите неполноту аксиоматической теории с одним бинарным отношением , удовлетворяющим аксиомам симметричности и антисимметричности.
5.8. Исследуйте на полноту аксиоматическую теорию AT (пример 4.1).
5.7*. Докажите неполноту аксиоматической теории
проективных плоскостей.
6. Формулировка аксиоматической
теории
В этом параграфе вводится понятия формулировки теории и независимости системы аксиом.
Как уже говорилось, неформальная теория T включает в себя некоторый список T0 неопределяемых терминов, список T1 определяемых терминов, список P0 аксиом и список P1 всех остальных высказываний, которые можно вывести из P0 по некоторым фиксированным логическим правилам. Назначение множества T0 состоит в том, чтобы получить из него множество T0 U T1 всех используемых в теории T терминов; аналогично, множество P0 нужно для получения множества P0 U P1 всех теорем теории T. Упорядоченную пару <T0, P0 > обычно называют формулировкой теории T.
Изучение теории T может привести нас к
обнаружению самых разнообразных и полезных
других ее формулировок. Задание какой-либо из
этих формулировок равносильно заданию
некоторого подмножества множества T0 U T1 и
подмножества
множества P0 P1,
состоящего из высказываний, выразимых в терминах
элементов множества
,
причем из высказываний, входящих в
, можно вывести все остальные
теоремы данной теории. Чтобы пара вида < T0,
P0> была формулировкой теории T,
достаточно, очевидно, чтобы термины из T0
могли быть определены через термины из
и чтобы высказывания из P0
могли быть выведены из высказываний из
.
Для многих общеизвестных аксиоматических теорий имеются различные формулировки. Различные формулировки какой-либо теории - это ни что иное, как различные возможные подходы к одной и той же математической структуре. В зависимости от принятых критериев можно предпочесть ту или иную из таких различных формулировок. Основаниями для такого предпочтения могут, например, служить соображения эстетического характера; важную роль может здесь играть и желание иметь как можно более простое множество аксиом, а также возможность более изящных доказательств теорем. Одни исследователи предпочитают какую-либо конкретную формулировку теории, находя ее более "естественной", нежели остальные. Другие стремятся располагать формулировкой, включающей минимальное количество первичных терминов или аксиом.
Казалось бы, от формулировки аксиоматической
теории ничего не зависит. Две разные
формулировки <T0, P0 > и
<,
> одной теории T определяют,
очевидно, одно и то же множество теорем. Однако,
исследователи, отправляясь от разных
формулировок, часто развивают теорию в различных
направлениях. При этом множество теорем,
доказанных исследователями, взявшими за основу
формулировку <T0, P0 >,
может значительно отличаться от множества
теорем, доказанных исследователями, взявшими за
основу формулировку <
,
>. Различные
формулировки теории во многих случаях
определяют различные направления исследований.
Так, например, теория графов и теория бинарных
отношений значительно отличаются друг от друга
наборами доказанных теорем, хотя по существу они
являются различными формулировками одной и той
же теории.
Формулировки неформальной теории можно характеризовать с помощью такого понятия, как независимость множества аксиом.
Определение 6.1. Множество аксиом называется независимым, если исключение любой аксиомы из этого множества приводит к уменьшению запаса теорем; в противном случае множество аксиом называют зависимым.
Отдельная аксиома (рассматриваемая как элемент множества аксиом некоторой формулировки) независима, если ее исключение из этого множества уменьшает запас теорем, и зависима в противном случае. Ясно, что независимая аксиома не может быть выведена из остальных аксиом. Разумеется, независимость какого-либо множества аксиом равносильна тому, что независима каждая аксиома из этого множества.
Рассмотрим непротиворечивую теорию T с
формулировкой <T0, P0 >,
и пусть A - одна из ее аксиом. Чтобы убедиться в
независимости аксиомы A от остальных аксиом , надо доказать, что ни A,
ни
нельзя вывести из
. Для этого достаточно
построить две модели теории
с формулировкой <T0,
> так, чтобы в одной из
них выполнялось предложение A (это будет
модель теории T), а в другой -
. Так как непротиворечивость теории T
считается установленной ранее, то первую модель
уже фактически строить не надо. Достаточно
построить вторую модель - модель теории с
формулировкой
.
Например, независимость системы аксиом A1, A2, A3 теории аффинных плоскостей может быть доказана посредством построения трех интерпретаций теории, для каждой из которых не выполняется одна из аксиом A1, A2, A3, а две другие выполняются (рис. 6.1).
Рис. 6.1. Три интерпретации для
доказательства независимости
аксиом A1, A2, A3 соответственно
Независимость не является обязательным
требованием для системы аксиом. Независимость
системы аксиом свидетельствует в известном
смысле об изяществе содержащей эту систему
формулировки теории. Не всегда для той или иной
аксиоматической теории целесообразно выбирать
независимую систему аксиом: изящество системы
аксиом может привести к громоздкости
доказательств теорем теории.
Упражнения
1. Докажите независимость множества аксиом {B1, B2, B3} теории эквивалентности (пример 3.2).
2. Проверьте на независимость систему аксиом
а) теории порядка (упражнение 5.1);
б) теории строгого линейного порядка (упражнение 5.3);
в) теории проективных плоскостей (упражнение 5.4).
г) тории AT (пример 4.1).
ЛИТЕРАТУРА
1. Е. П. Емельченков, В. Е. Емельченков. Бинарные отношения. Отношение эквивалентности. - Математическая морфология. - Смоленск: Изд-во СГМА, 1997. - Том 2. - Вып. 2. - С. 3-20.
2. Столл Роберт Р. Множества. Логика.
Аксиоматические теории. - М.: Просвещение, 1968.
THE AXIOMATIC THEORIES
E. P. Emelchenkov, V. E. Emelchenkov
We consider axiomatic method of mathematical theories's building. We
discuss characteristics of consistency and fullness of axiomatic theories.
Кафедра информатики
Смоленский государственный педагогический университет
Поступила 7.10.2000.