УДК 519.68 (075.8)

СРАВНЕНИЕ АЛГОРИТМОВ МАМДАНИ И СУГЭНО В ЗАДАЧЕ

АППРОКСИМАЦИИ ФУНКЦИИ

© 2001 г. В. В. Круглов

В статье на примере задачи аппроксимации функции проведено сравнение двух наиболее распространенных алгоритмов нечеткого вывода - Мамдани (Mamdani) и Сугэно (Sugeno).Установлено определенное преимущество алгоритма Сугэно - в плане точности и простоты реализации. Показано функциональное сходство данного алгоритма с обобщенно-регрессионной искусственной нейронной сетью (GRNN).

Среди других алгоритмов нечеткого вывода, пожалуй, наиболее известными и популярными являются алгоритмы Мамдани (Mamdani) и Сугэно (Sugeno). Рассмотрим данные алгоритмы применительно к задаче аппроксимации непрерывной функции одной переменной.

Алгоритм Мамдани. Отметим вначале, что используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:

П₁: если x есть A₁, тогда z есть B₁,

П₂: если x есть A₂, тогда z есть B₂,

. . . . . . . . . .

П_n: если x есть A_n, тогда z есть B_n,

где x - входная переменная (имя для известных значений данных), z - переменная вывода (имя для значения данных, которое будет вычислено); А_i и В_i - нечеткие множества, определенные соответственно на X и Z с помощью функций принадлежности и (z).

Пример подобного правила:

если x - низко, то z - высоко.

Механизм нечеткого вывода при аппроксимации функции z(x) можно представить в виде:

Предпосылка:

П₁: если x есть A₁, тогда z есть B₁,

П₂: если x есть A₂, тогда z есть B₂,

. . . . . . . . . .

П_n: если x есть A_n, тогда z есть B_n.

Факт: x есть A

---------------------------------------------

Следствие: z есть B

В рассматриваемой ситуации данный вывод в форме алгоритма Мамдани математически может быть описан следующим образом:

1. Введение нечеткости (fuzzification): для заданного (четкого) значения аргумента x = x0 находятся степени истинности для предпосылок каждого правила a_i = (x0).

2. Нечеткий вывод по каждому правилу: находятся "усеченные" функции принадлежности для переменной вывода:

= (a_i, ).

3. Композиция: с использование операции МАКСИМУМ (max) производится объединение найденных усеченных функций, что приводит к получению итогового нечеткого подмножества для переменной вывода с функцией принадлежности

(z) = = [].

4. Наконец, приведение к четкости (defuzzification) - для нахождения z0 = F(x0) - обычно проводится центроидным методом: четкое значение выходной переменной определяется как центр тяжести для кривой , т.е.

,

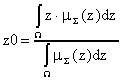
где W - область определения .

Алгоритм Сугэно (0-го порядка). Исходный набор правил представляется в виде

П_i: если x есть A_i, тогда z есть z_i, i = 1,2,…,n,

где z_i = z(x_i).

Алгоритм состоит всего из двух этапов. Первый этап идентичен первому этапу алгоритма Мамдани. На втором этапе находится (четкое) значение переменной вывода:

.

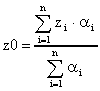
Возможность использования аппарата нечеткой логики для задач аппроксимации базируется на следующих результатах.

1. В 1992 г. Ванг (Wang) показал, что нечеткая система, использующая набор правил

П_i: если x_i есть A_i и y_i есть B_i, тогда z_i есть C_i, i = 1,2,…,n

при

1) гауссовских функциях принадлежности

, , ,

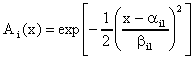
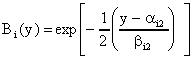
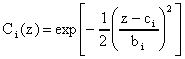
2) композиции в виде произведения

[A_i(x) and B_i(y)] = A_i(x)B_i(y),

3) импликации в форме (Larsen)

[A_i(x) and B_i(y)]®C_i(z) =A_i(x)B_i(y)C_i(z),

4) центроидном методе приведения к четкости

,

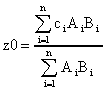
где c_i - центры C_i(z), является универсальным аппроксиматором, т.е. может аппроксимировать любую непрерывную функцию на компакте U с произвольной точностью (естественно, при ).

Иначе говоря, Ванг доказал теорему: для каждой вещественной непрерывной функции F(X), заданной на компакте U и для произвольного e>0 существует нечеткая экспертная система, формирующая выходную функцию (X) такую, что

,

где - символ принятого расстояния между функциями.

2. В 1995 году Кастро (Castro) показал, что логический контроллер Мамдани при

1) симметричных треугольных функциях принадлежности:

2) композиции с использованием операции min:

[A_i(x) and B_i(y)] = min{A_i(x),B_i(y)},

3) импликации в форме Мамдани и центроидного метода приведения к четкости

,

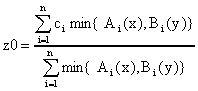
также является универсальным аппроксиматором.

Сравнение описанных алгоритмов выполнялось при следующих условиях:

· аппроксимации функции проводилась на отрезке [-1, 1];

· аппроксимируемая функция задавалась набором значений (x_i, z_i), i = 1,2,…,n, при этом точки z_i располагались эквидестантно;

· функции принадлежности имели вид функций Гаусса, т.е. (x) =j((x-x_i)/a), (z) = j((z-z_i)/b), где j(·) - функция Гаусса, j(s/s) = exp(-s²/2s²), s - параметр функции (соответственно, a или b).

· количество правил n задавалось a priori;

· значения параметров a и b варьировались для получения наилучшего качества аппроксимации при заданном n.

Реализация алгоритмов и соответствующие вычислительные эксперименты проводилась с помощью системы MathCAD 2000.

Некоторые результаты при n = 9, a = 0.1, b = 0.3 приведены в табл. 1 и 2.

Таблица 1. Результаты аппроксимации для функции F(x) = x²

Таблица 2. Результаты аппроксимации для функции F(x) = x³

Приведенные и другие аналогичные результаты (полученные для большого числа вариантов) позволяют сделать выводы:

1) при прочих равных условиях и при оптимальных параметрах a и b погрешность аппроксимации с применением алгоритма Сугэно несколько меньше, чем с применением алгоритма Мамдани;

2) алгоритм Сугэно с вычислительной точки зрения реализуется значительно проще, чем алгоритм Мамдани, а время счета для него меньше, чем для алгоритма Мамдани в 50-100 раз;

3) общий вывод: если нет каких-либо особенных доводов в пользу алгоритма Мамдани, то лучше использовать не его, а алгоритм Сугэно.

Данные выводы, разумеется, носят предварительный характер и нуждаются в более корректном подтверждении (для функций многих переменных и т.п.).

В заключение приведем еще один результат, устанавливающий связь между алгоритмом Сугэно, так называемой обобщенно-регрессионной нейронной сетью (GRNN) и непараметрической оценкой регрессии Надарая-Ватсона [2].

Указанная сеть предназначена для решения задач регрессии (аппроксимации), при этом ее выход формируется как взвешенное среднее выходов по всем обучающим наблюдениям:

, (1)

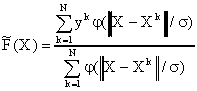
где X^k, y^k - точки обучающей выборки (X - в общем случае векторный аргумент); j(·) - отмеченная функция Гаусса.

Поясним данную формулу и название сети.

Предположим, что элементы обучающей выборки - случайные величины, с совместной плотностью вероятности p₂(X,y), при этом, как известно, условное математическое ожидание M(y/X) называется регрессией (обобщенной регрессией) и определяется соотношением

, (2)

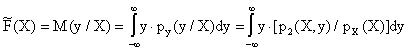
где - условная плотность вероятности y по X, - безусловная плотность вероятности случайной величины X.

Примем в последнем выражении аппроксимации:

, ,

где d(·) - обозначение дельта-функции Дирака.

Подстановка данных аппроксимаций в (2) дает:

.

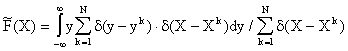
Изменение порядка выполнения операций интегрирования и суммирования (здесь это допустимо и корректно) и использование, далее, свойств дельта-функции позволяет записать:

.

Аппроксимация теперь дельта-функции функцией Гаусса приводит к выше представленному выражению для выхода обобщенно-регрессионной нейронной сети; приведенный вывод собственно и поясняет ее название.

Но, если в формуле (1) принять обозначения z_k = y^k и a_k = j((X - X^k)/s), то функционирование такой сети формально можно считать подобным функционированию системы, реализующей приведенный алгоритм Сугэно 0-го порядка (упрощенный алгоритм нечеткого вывода [1]), при этом величины a_k в данном случае - степени "истинности" продукционных правил при заданных (гауссовых) функциях принадлежности j(·) и значении переменной входа, равной X^k.

Более того, выражение (1), описывающее, как установлено, выход сети GRNN и алгоритма нечеткого вывода Сугэно, полностью совпадает с непараметрической оценкой регрессии, известной как оценка Надарая-Ватсона, для которой доказана следующая теорема о сходимости [2].

Теорема. Оценка, определяемая формулой (1), если j(·) - функция Гаусса, при выполнении условий

N®Ґ, s_N®0, N®0

где s_N - параметр функции Гаусса, в данном случае зависящий от объема обучающей выборки, m - размерность вектора X,

сходится к F(X) с вероятностью 1.

Приведенный результат является теоретическим обоснованием алгоритма Сугэно как универсального аппроксиматора.

ЛИТЕРАТУРА

1. Круглов В. В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Радио и связь, 2000.

2. Катковник В. Я. Непараметрическая идентификация и сглаживание данных: метод локальной аппроксимации. - М.: Наука, 1985.

COMPARISON OF ALGORITHMS MAMDANI AND SUGENO IN A TASK APPROXIMATIONS OF FUNCTION

V.V. Kruglov

In the article on the example of a task of approximation of function conducted comparison of two the most wide-spread algorithms of fuzzy conclusion - Mamdani and Sugeno. Installed the certain advantage of algorithm Sugeno - in the plan of accuracy and simplicity of realization. The functional similarity of the given algorithm with general regression artificial neural network (GRNN) is shown.

Кафедра Управления и информатики

Филиал Московского энергетического института

(Технического университета) в г. Смоленске

Поступила в редакцию 26.01.2001.