НАУКОМЕТРИЧЕСКИЙ
АНАЛИЗ СТАТИСТИЧЕСКОЙ ПАРАДИГМЫ
ЭКСПЕРИМЕНТАЛЬНОЙ БИОМЕДИЦИНЫ © 2001 г. В.П.Леонов В работе приведены результаты наукометрического анализа 1540 отечественных и 392 зарубежных журнальных статей биометриченской тематикию. Все статьи были опубликованы в последние 10 лет в 34 отечественных и 20 зарубежных журналах. Цель анализа - оценка относительных частот применения различных методов статистики, сравнение этих частот между собой, и реконструкция на их основе статистической парадигмы в отечественной биомедицине. Установлено наличие сдвиговой парадигмы, отражающей представление о том, что основное различие между группами сравнения заключается в сдвиге среднего значения исследуемой переменной. Такой подход можно идентифицировать как одномерный, механистический взгляд на сугубо многомерные системы. Последнее десятилетие для отечественной биомедицины характеризуется бурным внедрением в исследовательскую практику персональных компьютеров. Однако совпадение этого внедрения по времени с экономическим спадом и отечественная специфика финансирования биомедицинской науки деформировали этот процесс. В результате чего широкое использование компьютеров в отечественной биомедицине не привело к качественному скачку в статистической методологии этих исследований [1-5, 9]. За рубежом данный процесс происходил порядка 20-25 лет назад и в настоящее время результаты его достаточно очевидны. Приведем несколько цитат из книги С.Гланца "Primer of Biostatistics", недавно переведенной в России. "С тех пор многое изменилось. Важность грамотного использования статистических методов осознается все шире. И, хотя ошибки не исчезли, все больше журналов прилагают усилия к их искоренению. Во многих из них рецензирование включает отдельный этап проверки статистической правильности предлагаемых работ. Приведу подтверждение, наиболее ощутимое для меня. Я являюсь внештатным редактором Journal of the American College of Cardiology, и моя работа состоит в выявлении статистических ошибок в поступающих статьях. Доля статей, содержащих ошибки, как и раньше, составляет около половины, но теперь уже половины предлагаемых к публикации, а не опубликованных работ." Представляет несомненный интерес сравнение статистических технологий отечественных исследователей и их зарубежных коллег. Не менее важно попытаться на основе этого анализа сформулировать доминирующую в отечественной биомедицине статистическую парадигму. В данной работе приведены результаты наукометрического анализа 1540 отечественных и 392 зарубежных журнальных статей биомедицинской тематики. Все статьи были опубликованы в один и тот же период - в последние 10 лет. Были изучены 34 ведущих отечественных биомедицинских журнала, среди которых был и "Сибирский медицинский журнал". 392 англоязычные статьи были опубликованы в журналах "Journal of Experimental Medizine", "Journal of Immunology", "Nature Genetics", "Journal of Cell Biology", "American Journal of Cardiology", "American Journal of Hypertension", "American Journal of Pathology", "American Journal of Clinical Pathology", "Biologische Medizin", "Biomedicine and Pharmacotherapy", "BMJ", "British Journal of Radiology", "Cancer", "Epidemiologie, Microbiologie, Immunologie", "European Psychiatry", "Immunology and Cell Biology", "JAMA", "Ecology", "General Physiology and Biophysics", "New England Journal of Medicine". Целью анализа была оценка относительных частот применения авторами русско- и англоязычных журналов различных методов статистики, сравнение этих частот между собой, а также реконструкция модели статистической парадигмы доминирующей в отечественной биомедицине на основе анализа структуры этих частот. Статистические аргументы или … статистические гитики? Статистические методы использовались в 82% отечественных статей (R-статьи), в зарубежных публикациях (E-статьи) эта доля составила 87%. Однако в 52% R-статей авторы вообще никак не описывали используемые ими методы статистики. О том, что авторы применяли методы статистики, можно было догадаться только по выражениям вида "р < 0,05" и (М ± m), поскольку выражения типа "р<0,05" или "p<0,01" могут быть получены только при использовании конкретных статистических критериев. Напротив, в 83% E-статей сообщается, с помощью каких именно статистических критериев производилась проверка конкретных гипотез. Для многих R-статей характерно наличие в описании методов статистики бессмысленных и абсурдных выражений, представляющих собой комбинации так называемых "мемов" - клише, заимствованных из других работ. Детальный анализ этих мемов обнаруживает их камуфляжный характер, вследствие чего несколько лет назад нами было введено понятие "камуфляжного мема". По своему языку и стилю такие описания созвучны речи героев произведений А. Платонова "Котлован" и "Чевенгур", или высказываниям экс-премьера Черномырдина В.С. ("У меня нет вопросов к русскому языку", "…моя специальность и жизнь проходили в атмосфере нефти и газа"). Примеры таких описаний даны в работе "Долгое прощание с лысенковщиной". Приведем лишь два из них: "Вероятность случайности различий соответствует достоверности", "Различие считалось достоверным при p < 0,05, т.е. в тех случаях, когда вероятность различия составляла больше 95%". Обилие подобных недостатков в текстах биомедицинских статей и диссертаций свидетельствует как минимум о четырех вероятных причинах этого явления. Во-первых, низкая статистическая культура исследователей. Причины этого достаточно очевидны: в медицинских вузах готовят врачей, а не исследователей, и поэтому выпускники этих вузов не имеют необходимой для исследователя статистической подготовки. Этот же вывод можно сделать и на основе содержания Приложений 14 и 15 к приказу Минздрава РФ от 25.12.97 № 380 [7]. Во всех аналогичных квалификационных характеристиках в разделе "Знание смежных дисциплин" вообще отсутствует упоминание математики. И это вполне разумно, поскольку медицинский вуз не может, да и не должен обеспечивать своим выпускникам профессиональный уровень владения биометрикой. Его задача подготовить хороших врачей, лекарей, а не специалистов по биостатистике.Сказывается до сих пор и последствия периода "лысенковщины", когда математика, и особенно статистика, активно изгонялись из биологии и медицины. Во-вторых, это отсутствие в структурах биомедицинских НИИ и вузов специализированных лабораторий биостатистики, призванных обеспечить исследователю квалифицированный статистический анализ наблюдений. Немногочисленные лаборатории имеющиеся в таких НИИ и вузах (ЦНИЛ), комплектуются в основном теми же выпускниками медвузов. Редко где в них работают специалисты с соответствующим образованием. Помимо всего прочего, отсутствие таких лабораторий не позволяет дать основы системного подхода с грамотной формулировкой статистических гипотез аспирантам и докторантам, проводящим свои исследования в этих НИИ и вузах. Третья причина - отсутствие отраслевой нормативной базы (отраслевые стандарты, стандарты предприятий и т.п.) регламентирующей этап статистического анализа. Парадоксально, но сегодня анализ крови или мочи выполняется в лабораториях по утвержденным Минздравом документам, и только людьми со специальным образованием. Тогда как статистический анализ экспериментальных данных - завершающий этап кропотливой работы многих специалистов, в большинстве случаев выполняется самоучками, людьми не имеющими профессиональной подготовки в этой области. Четвертая причина - отсутствие квалифицированной статистической экспертизы в редакциях журналов, диссертационных и экспертных советах ВАК, что говорит об отсутствии в них специалистов владеющих данными технологиями [4]. Впрочем, это отсутствие может быть и не случайным, поскольку повышение уровня требований к статистической корректности статей и диссертаций сразу же приведет к их уменьшению. Нетрудно догадаться, чем это грозит для периодических изданий и диссертационных советов. Наличие этой проблемы уже начинают признавать наиболее прогрессивные редакторы отечественных медицинских журналов. Так в статье "СТАТИСТИКА УМЕЕТ МНОГО ГИТИК", [5] президент издательства "МедиаСфера", издающего около 20 отечественных медицинских журналов, С.Е. Бащинский, пишет: "По сути, эти клише представляют собой магические заклинания, служащие, по мысли авторов, "пропуском в науку". … Статистике в биомедицинских исследованиях отводится роль "гитик", звучные и непонятные авторам термины нужны для достижения основной цели — придания работе научного "веса", достаточного для опубликования в журнале или для защиты диссертации. Редакторы научных журналов, публикующие подобные статьи, вольно или невольно становятся соучастниками игры в научный "фокус": в надежность результатов исследования изначально никто не верит, свидетельством его научности становится сам факт публикации, а важнейшим условием публикации —упоминание о статистических "гитиках". Так будет происходить до тех пор, пока редакторы, устанавливающие правила игры, не объявят о серьезности своих намерений отбирать и публиковать только действительно научные статьи". Какие статистические методы и критерии предпочитают авторы R-статей Ниже в табл.1 приведены результаты сравнения относительных частот использования статистических методов и критериев в русскоязычных и англоязычных журналах. Общее количество статистических методов и критериев, использованных в англоязычных статьях, составило более 100. Из этого многообразия мы выбрали только наиболее известные, объединив их в 53 группы. После оценки относительных частот использования того или иного метода в R- и Е-статьях, производилась проверка статистической гипотезы о равенстве этих пропорций с использованием Z-критерия [6]. Для 51 группы достигнутые уровни значимости "р" имели значение гораздо меньшие 5%, что позволяет утверждать статистически значимое различие этих частот. Только для парных коэффициентов корреляции Пирсона (р=0,1445) и нелинейных преобразований переменных (р=0,0961) были приняты нулевые гипотезы о равенстве частот использования этих методов в R- и Е-статьях. Для всех остальных групп сравнения эти частоты отличались статистически значимо (р << 0,05). Для сравнения приоритетов в группах полученные результаты в табл.1 отсортированы по убыванию относительных частот. Табл. 1. Частота использования статистических методов и критериев в R- и Е-статьях
Сложные проблемы
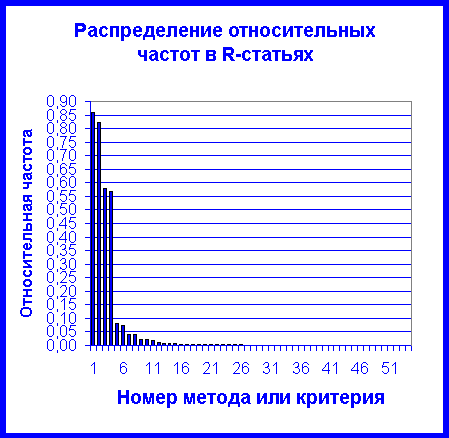
всегда имеют простые, Итак, согласно табл.1 после дескриптивных статистик и выражений типа "р < …." отечественные исследователи предпочитают проверку гипотез о равенстве двух средних с использованием t-критерия Стьюдента. Практически во всех работах вообще не проверяются условия возможности применения этого критерия, что приводит к сомнительности полученных авторами выводов. С многочисленными примерами таких работ читатели могут познакомиться в разделе "КУНСТКАМЕРА". (Аналогичный раздел КУНСТКАМЕРА появился и в журнале ТИРОНЕТ, редакция которого решила, что "... терпеть “ТИРОБРЕД” сил больше нет.") Разница между значениями частот в третьей и четвертой строках (0,5805 и 0,5662) таблицы объясняется тем, что в ряде статей авторы просто упоминали об использовании t-критерия Стьюдента, но не приводили его значения. Отметим также, что следующий за критерием Стьюдента метод - оценка коэффициентов корреляции Пирсона, имеет частоту почти в 7 раз меньше, чем у предшествующего метода. Иными словами, скачок в 48,5% между частотой применения критерия Стьюдента и корреляцией по Пирсону, означает дискретность нашего распределения и безусловное доминирование сравнения двух средних по Стьюденту по отношению ко всем остальным методам и критериям. Обратим также внимание на то, что
частота проверки нормальности распределения,
которую необходимо проводить в обязательном
порядке при использовании критерия Стьюдента,
примерно в 944 раза меньше, чем частота
использования критерия Стьюдента. Тогда как
проверка равенства двух генеральных дисперсий,
также обязательное условие при использовании
критерия Стьюдента, в R-статьях вообще не
проводилась. Сумма всех прочих методов и
критериев, кроме критерия Стьюдента и
дескриптивных статистики, составляет 0,3773.
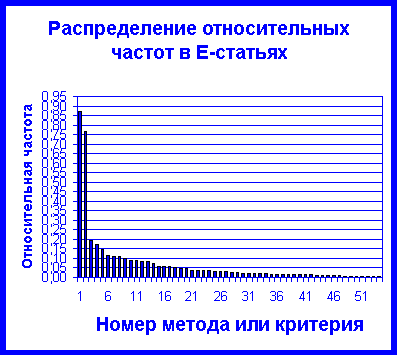
Около 50% говорили о нормальности распределения, однако не могли при этом объяснить, как реально проверить нормальность распределения. О необходимости выполнения второго обязательного условия вообще никто из опрашиваемых не говорил... За последние 10 лет нами был выполнен статистический анализ более 200 массивов реальных биомедицинских данных. Эти исследования показали, что в 50 -70% случаев биомедицинские количественные показатели не подчиняются нормальному распределению. Наиболее характерно это для групп больных пациентов или экпериментальных образцов исследуемых объектов. К чему приводит игнорирование условий применения этого критерия мы показали в работах [1] и [9]. Между тем, с упорством достойным лучшего применения, многочисленные отечественные исследователи продолжают эту порочную практику. Особенно характерно это для авторов "Бюллетеня экспериментальной биологии и медицины", для которых в КУНСТКАМЕРЕ даже открыта специальная экспозиция . Проведенный нами анализ публикаций в выпусках этого журнала за 2000г. показал, что подавляющее большинство статей содержат сомнительные результаты, полученные именно вследствие некорректного применения t-критерия Стьюдента! Наиболее типичен в этом отношении 10-й выпуск этого журнала за 2000г. Какие статистические методы и критерии предпочитают англоязычные авторы Из данных табл.1 мы видим, что
характер распределения частот используемых
методов и критериев в Важным моментом этого
распределения частот является достаточно
высокая доля 11 сугубо многомерных методов, таких
как множественный регрессионный анализ (0,0816) ,
анализ главных компонент (0,0485), дискриминантный
анализ (0,0459), факторный анализ (0,0383), теории
планирования экспериментов (0,0357), оценка частных
коэффициентов корреляции (0,0357), кластерный
анализ (0,0306), ковариационный анализ (0,0179), анализ
канонических корреляций (0,0128), многомерное
шкалирование (0,0102), логлинейный анализ (0,0077) и
анализ соответствий в таблицах сопряженности
(0,0051). Общая доля этих многомерных методов
составляет 0,3343, т.е. в каждой третьей E-статье
используются многомерные методы. Из 11
перечисленных выше многомерных методов в
R-статьях обнаружены только 7, суммарная доля
которых составила 0,0322. Таким
образом, зарубежные исследователи в 10 раз чаще
используют многомерные методы, нежели авторы
R-статей. Это говорит о том, что статистическая
парадигма зарубежных исследователей содержит
выраженный многомерный подход к исследованию
изучаемых объектов.
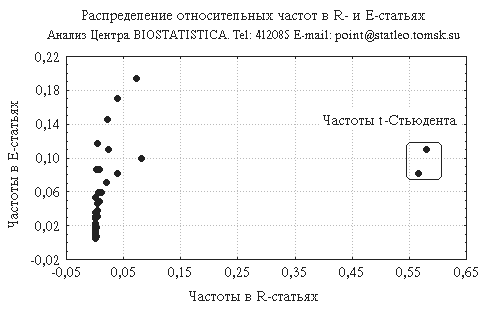
исследований является не столько обнаружение локального эффекта, сколько оценка совокупной связи этого эффекта с длительностью жизни пациентов. Ниже на рис.3 в осях относительных частот по каждой из сравниваемых групп представлено распределение частот используемых статистических методов.
Используя результаты данного наукометрического анализа, попытаемся сформулировать доминирующую в российской биомедицинской науке статистическую парадигму, которая проявляет себя как латентная, скрытая закономерность только при анализе достаточно большого количества публикаций [2-5]. Суть этой парадигмы, названной нами СДВИГОВОЙ, заключается в доминировании у отечественных экспериментаторов в области биологии и медицины представления о том, что основное (а возможно и единственное!) различие между группами сравнения заключается в тривиальном, механическом сдвиге среднего значения исследуемой переменной. При этом игнорируются все остальные не менее важные параметры распределения признака, такие как меры рассеяния (дисперсия, размах и т.д.) и меры формы (эксцесс и асимметрия), корреляции между признаками и т.д. Более того, игнорируются возможные и весьма важные изменения законов распределения вероятностей в сравниваемых группах, изменения структуры связей между объектами исследования. Можно идентифицировать такой подход как одномерный, механистический взгляд на сугубо многомерные взаимодействующие системы. Очевидно, что такой подход является деформацией нормальной научной методологии, базирующейся на системном анализе. Для иллюстрации ущербности такой парадигмы приведем искусственный пример. Предположим, что мы поставили задачу сравнить между собой температуру тела персонала больницы с температурой тела всех пациентов этой больницы. Проверка (статистически вполне корректная) показала, что средние температуры двух сравниваемых групп статистически значимо не различаются. Между тем эти две группы имеют принципиальное различие в вариации этого показателя. Действительно, если принять во внимание, что персонал больницы исполняет свои обязанности будучи здоровым, то разброс температуры персонала будет сравнительно мал. Иное дело пациенты этой больницы, среди которых будут находиться больные с повышенной температурой, выздоравливающие пациенты с нормальной температурой, и те, кто недавно поступил в морг. В результате средняя температура пациентов будет равна средней температуре персонала, однако существенное различие групп по этому показателю будет заключаться в минимальных и максимальных значениях. Несмотря на искусственный характер этого примера, в реальных исследованиях такая ситуация встречается достаточно часто. Причем именно эти минимальные и максимальные значения, как правило, и несут нередко важнейшую информацию о сравниваемых группах. Крайне редкое применение многомерных статистических методов говорит о том, что исследуемые признаки изучаются авторами в неявном предположении об изолированности отдельных подсистем объекта друг от друга. Несмотря на то, что исследователи изучают изначально многомерные системы, независимо от того, организменный или клеточный это уровень, их анализ фактически не поднимается выше одномерных подсистем. Более того, это еще и свидетельство того, что авторы подобных публикаций, зная о существовании таких взаимосвязей в исследуемых объектах, игнорируют этот аспект, и сужают тем самым собственное исследование до более утилитарных и коньюктурных целей. В результате применение статистики в исследовании становится не инструментом поиска нового знания, а средством онаучивания заранее продекларированного эффекта изменения среднего значения того или иного признака. Деструкция важнейшего элемента системного анализа - выделение структуры и исследование связей между частями этой структуры, и приводит в итоге к "статистическим гитикам"... Игнорирование этой деформации научной методологии со стороны Минздрава РФ, РАМН, Минобразования РФ, ВАК РФ и руководителей НИИ РАМН и журнальных редакций приводит к воспроизведению одних и тех же статистических нелепиц в сотнях и тысячах статей и диссертаций биомедицинской тематики. Повышению экономической эффективности и качества экспериментальных биомедицинских исследований способствовало бы создание в биомедицинских НИИ и отделениях РАМН специализированных лабораторий биостатистики, разработка соответствующих отраслевых стандартов, а также введение независимой статистической экспертизы в редакциях биомедицинских журналов (что является обычной практикой за рубежом), в диссертационных и экспертных советах ВАК. Два года назад статьей "В новый век -
с доказательной биомедициной"
опубликованной 21 мая 1999 г. в 20 выпуске газеты
"ПОИСК" было открыто обсуждение проекта
нового "Положения ВАК РФ...". В ней, среди
прочих предложений, была высказана идея об
организации выпуска на лазерных компакт-дисках
профилированных ежегодных сборников
авторефератов и самих диссертаций, защищаемых в
России в области биомедицины. При этом вполне
естественным было бы введение требования о сдаче
в диссертационные советы, и в ВАК или ВИНИТИ,
электронных копий диссертаций. Вновь это же
предложение прозвучало в статье "Куплю 500
диссертаций" ("Медицинская
газета", 14 февраля 2001г.). Однако в обоих
случаях руководство Минздрава и Минобразования
РФ, РАН, РАМН и ВАК РФ так и не рискнуло
обнародовать свое отношение к предложениям
высказанным в этих статьях. Между тем за рубежом
в марте 2001 г. под эгидой ЮНЕСКО был проведен уже 4-й международный симпозиум
ETD 2001 по данной тематике, на котором
присутствовали представители 15 стран. Уже
организуется и международная
сеть подобных библиотек, в которой более 100
членов.
Литература.
|