УДК 519.1
АВТОМАТНОЕ МОДЕЛИРОВАНИЕ ПОТОКА ИСТОРИЧЕСКИХ СОБЫТИЙ
© 2001 г. В. И. Левин
Рассмотрена проблема математического моделирования суммарного потока однородных исторических событий, получаемого суммированием аналогичных региональных потоков. Введены различные характеристики моделируемого потока событий. Показана возможность моделирования потоков с помощью динамического автомата без памяти. При этом региональные потоки событий моделируются входными процессами автомата-модели, суммарный поток событий - его выходным процессом, а соотношение региональных и суммарных потоков - логической функцией автомата. Построенная модель позволяет анализировать суммарный поток исторических событий методами аналитической динамики конечных автоматов.
1. Введение
За долгие годы существования человечество накопило богатый опыт эффективного применения математики сначала в естественных науках - физике, астрономии, химии, а затем в технике. Иначе обстояло дело в гуманитарных науках, где всегда были распространены словесные описания сложных явлений, что часто приводило к результатам, не поддающимся сравнительному анализу, не говоря уже о характере изложения- многословном и нередко неоднозначном по смыслу. Конечно, гуманитарные системы трудно поддаются количественному анализу, что вызвано присутствием в них человека, вносящего в поведение таких систем неопределенность. Однако "трудно" не значит "невозможно", и многие гуманитарные системы вполне поддаются описанию подходящими математическими средствами. Язык математики может логично, строго и однозначно выражать конструкции, которые прежде излагались только словесно. Более того, благодаря компактности, этот язык позволяет в ряде случаев вскрывать неизвестные ранее закономерности. Благодаря этим достоинствам математические методы за последние несколько десятилетий проникли в такие гуманитарные науки, как экономика, социология, психология, политология, лингвистика, литературоведение, история, право, менеджмент, экология и т.д. Спектр применяемых здесь математических средств сейчас очень широк, но их распределение между различными гуманитарными науками весьма неравномерно. Так, в экономике используют математический анализ, теорию вероятностей и матстатистику, теорию оптимизации, графы и много других методов, в то время как в праве используется лишь математическая логика. По-видимому, мы находимся на этапе выработки наиболее необходимых для гуманитарных наук математических методов, подобных тем, которые в свое время были разработаны для естественных наук.
Положение исторической науки с точки зрения используемых в ней математических методов специфично - здесь наблюдается почти полное господство вероятностно-статистических методов [1]. Общеизвестны достоинства этих методов, позволяющих строго и обоснованно анализировать закономерности поведения разнообразных систем со случайными параметрами, имеющими некоторые распределения вероятностей [2]. Однако их применение к изучению исторических событий имеет ряд очевидных существенных недостатков. Во-первых, поведение человека как движущей силы исторического процесса следует характеризовать как не имеющее определенного распределения вероятностей, что связано со свободой его воли. Во-вторых, при повторении поведенческих актов человека невозможно обеспечить их независимость, так как человек всегда действует с учетом прошлого опыта. В то же время, фундамент теории вероятностей - понятие вероятности - вводится с использованием понятия последовательности независимых опытов, частота появления в которых данного события и определяет его вероятность. В-третьих, указанные опыты должны характеризоваться одинаковыми условиями их проведения, а это требование практически невыполнимо, как по отношению к отдельному человеку, так и к историческим событиям, происходящим с участием людей.
Таким образом, поиск новых математических методов, позволяющих адекватно моделировать процессы и объекты, изучаемые исторической наукой, является важной и актуальной задачей.
В настоящей работе излагается новый оригинальный метод математического моделирования исторического процесса, основанный на теории динамических конечных автоматов [3-5] и математическом аппарате непрерывной (бесконечнозначной) логики [6]. Указанные теория и аппарат разработаны в течение последних 25 лет, а технология их применения для моделирования различных (в основном, технических и экономических) систем - за последние 10 лет [7]. Достоинство разработанного метода заключается в его конструктивности, позволяющей свести проблему математического моделирования исторического процесса к хорошо изученной задаче нахождения отклика автомата-модели процесса на заданные входные воздействия. Все это делает данный метод простым и удобным как для практического применения, так и для целей обучения.
2. Постановка задачи
Рассмотрим некоторое число n регионов
(частей света, стран, областей и т.д.), в которых
происходят однородные по своей природе
исторические события - войны, восстания,
образование новых и падение прежних государств,
крупные эпидемии или экологические катастрофы и
т.д. Каждый регион будем считать элементарным в
том смысле, что одновременно в нем может
происходить не более одного исторического
события рассматриваемого вида. В соответствии с
этим предположением каждый i-й регион (i=1,2,...,,n)
можно охарактеризовать, задав следующую
последовательность временных интервалов![]() , в каждом из которых
происходит по одному событию, а вне их события не
происходят. Здесь
, в каждом из которых
происходит по одному событию, а вне их события не
происходят. Здесь ![]() -
общее число интервалов для i-го региона, в которых
происходили события изучаемого вида. Будем
изучать суммарный поток событий, получаемый
суммированием потоков событий в отдельных
регионах. Нас будут интересовать, во-первых,
различные количественные характеристики
суммарного потока событий, определяющие
распределение этого потока во времени и
пространстве, и во-вторых, возможность анализа
поведения суммарного потока, исходя из
полученных данных о его текущем поведении
(текущих количественных характеристиках).
-
общее число интервалов для i-го региона, в которых
происходили события изучаемого вида. Будем
изучать суммарный поток событий, получаемый
суммированием потоков событий в отдельных
регионах. Нас будут интересовать, во-первых,
различные количественные характеристики
суммарного потока событий, определяющие
распределение этого потока во времени и
пространстве, и во-вторых, возможность анализа
поведения суммарного потока, исходя из
полученных данных о его текущем поведении
(текущих количественных характеристиках).
3. Общие сведения о динамических автоматах и непрерывной логике
В 1971-72 г.г. автором было показано, что
для описания динамических процессов в конечных
динамических автоматах адекватным
математическим аппаратом является непрерывная
логика в виде алгебры логики ![]() , где С - несущее множество в форме отрезка
вещественных чисел С=[А,В],
, где С - несущее множество в форме отрезка
вещественных чисел С=[А,В], ![]() =max и
=max и ![]() =min -
непрерывно-логические операции над С, называемые
соответственно дизъюнкцией и конъюнкцией. На
этой базе была разработана аналитическая
динамика конечных автоматов, позволяющая
вычислять, компактно представлять,
анализировать и синтезировать динамические
процессы в сложных схемах автоматов при сложных
входных воздействиях [3-5].
=min -
непрерывно-логические операции над С, называемые
соответственно дизъюнкцией и конъюнкцией. На
этой базе была разработана аналитическая
динамика конечных автоматов, позволяющая
вычислять, компактно представлять,
анализировать и синтезировать динамические
процессы в сложных схемах автоматов при сложных
входных воздействиях [3-5].
Рассмотрим простейший объект
разработанной теории - динамический конечный
автомат без памяти. Такой автомат имеет
некоторое число n входов, на которые действуют
двоичные сигналы ![]() ,
принимающие значение 0 или 1; некоторое число m
выходов, с которых снимаются двоичные сигналы
,
принимающие значение 0 или 1; некоторое число m
выходов, с которых снимаются двоичные сигналы ![]() со значениями 0 или 1.
Зависимость выходных сигналов, действующих в
произвольный момент времени, от действующих в
тот же момент входных сигналов задается с
помощью соответствующей автомату системы
булевых логических функций fi , т.е.
со значениями 0 или 1.
Зависимость выходных сигналов, действующих в
произвольный момент времени, от действующих в
тот же момент входных сигналов задается с
помощью соответствующей автомату системы
булевых логических функций fi , т.е.
![]() . (1)
. (1)
Реально и входные ![]() и выходные
и выходные ![]() сигналы
автомата зависят от времени t, т.е. являются
некоторыми двоичными процессами
сигналы
автомата зависят от времени t, т.е. являются
некоторыми двоичными процессами ![]() (t),
(t), ![]() (t).
При этом преобразование входных процессов в
выходные осуществляется согласно (1), т.е.
(t).
При этом преобразование входных процессов в
выходные осуществляется согласно (1), т.е.
![]() . (2)
. (2)
Динамический конечный автомат без
памяти реализуется, т.е. может быть представлен
структурно, так называемой асинхронной
комбинационной схемой из логических элементов
(реализующих элементарные булевы логические
функции). Реакция, получаемая на выходе
логического элемента в ответ на подаваемые на
него входные процессы, называется динамическим
процессом в элементе. Совокупность динамических
процессов во всех элементах асинхронной
комбинационной схемы называется динамическим
процессом в этой схеме. Задача расчета (анализа)
динамики конечного динамического автомата без
памяти заключается в нахождении (анализе)
динамического процесса во всех узлах (в
частности, на выходах) соответствующей
асинхронной комбинационной схемы по заданным
процессам на ее входах. Эта задача удобнее всего
решается методом подстановок: 1) схема автомата
разбивается на последовательные ступени
глубиной в один логический элемент; 2) с помощью
базовых операций непрерывной логики - дизъюнкции
и конъюнкции - находятся соотношения F между
входными и выходными процессами всех типов
элементов схемы; 3) по заданным входным процессам
схемы ![]() и найденным
соотношениям F определяются сначала процессы на
выходах 1-й ступени, по ним - процессы на выходах
2-й ступени и т.д. и, наконец, процессы
и найденным
соотношениям F определяются сначала процессы на
выходах 1-й ступени, по ним - процессы на выходах
2-й ступени и т.д. и, наконец, процессы ![]() на выходах всей схемы.
на выходах всей схемы.
Моменты изменения сигнала во всех вычисленных процессах выражаются через моменты изменения сигнала в заданных входных процессах схемы с помощью операций дизъюнкции и конъюнкции непрерывной логики.
В качестве примера приведем
простейшие соотношения F между входными и
выходными процессами двух двухвходовых
логических элементов: дизъюнктора (![]() ) и конъюнктора (&), реализующих
следующие булевы логические функции
) и конъюнктора (&), реализующих
следующие булевы логические функции
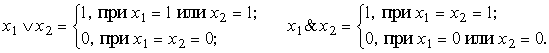 (3)
(3)
Обозначим ![]() изменение
сигнала 1
изменение
сигнала 1![]() 0 в момент
0 в момент ![]() ;
; ![]() -
изменение сигнала 0
-
изменение сигнала 0![]() 1 в
момент
1 в
момент ![]() . Тогда
указанные соотношения F запишутся в виде
. Тогда
указанные соотношения F запишутся в виде
 (4)
(4)
В формулах (4) ![]() и
и
![]() означают операции
дизъюнкции и конъюнкции непрерывной логики.
означают операции
дизъюнкции и конъюнкции непрерывной логики.
4. Высокоразмерные динамические автоматы
Изложенная в п.3 процедура изучения
динамики конечного динамического автомата без
памяти значительно усложняется в случае высокой
размерности автомата, т.е. когда число входов
и/или выходов в реализующей его асинхронной
комбинационной схеме велико либо когда велико
число изменений сигнала во входных процессах
этой схемы. Для преодоления возникающего здесь
"проклятия размерности" используют набор
следующих приемов [4-6]: 1) канонизация входных
воздействий схемы автомата, т.е. представление
процессов на входах схемы в канонической
(стандартной) форме, не зависящей от числа входов
схемы и числа изменений сигнала во входных
процессах; 2) введение специальных функций -
логических определителей ![]() различных рангов r от квазиматриц
различных рангов r от квазиматриц ![]() с различными длинами
строк - каждый такой определитель равен r-му по
возрастанию элементу матрицы и может быть
выражен соответствующей непрерывно-логической
функцией.
с различными длинами
строк - каждый такой определитель равен r-му по
возрастанию элементу матрицы и может быть
выражен соответствующей непрерывно-логической
функцией.
Канонизация входных воздействий возможна только для схем, реализующих симметрические логические функции своих входов, т.е. функции, одинаково (симметрично) зависящие от всех своих аргументов и потому принимающие определенное значение лишь в соответствии с числом аргументов со значением 1, независимо от того, какие именно это аргументы. Однако это не ограничивает общности рассмотрения, так как любая асинхронная комбинационная схема может быть реализована только из логических элементов с симметрическими булевыми логическими функциями. Общая форма канонизации входных воздействий схемы формулируется так.
Теорема 1. Любое воздействие в виде
процессов ![]() на n входах
асинхронной комбинационной схемы, реализующей
на всех своих выходах симметрические булевы
логические функции входов, можно представить
однозначно эквивалентной, с точки зрения
получаемых реакций на выходах, совокупностью
свободных (т.е. допускающих перенос с любого
входа на любой другой вход) импульсов 1(
на n входах
асинхронной комбинационной схемы, реализующей
на всех своих выходах симметрические булевы
логические функции входов, можно представить
однозначно эквивалентной, с точки зрения
получаемых реакций на выходах, совокупностью
свободных (т.е. допускающих перенос с любого
входа на любой другой вход) импульсов 1(![]() ), r=
), r=![]() в интервалах (
в интервалах (![]() ),
упорядоченных во времени линейно согласно
),
упорядоченных во времени линейно согласно ![]() . Здесь
. Здесь ![]() - момент r-го по возрастанию изменения
сигнала вида 0
- момент r-го по возрастанию изменения
сигнала вида 0![]() 1,
1, ![]() - момент r-го по
возрастанию изменения сигнала вида 1
- момент r-го по
возрастанию изменения сигнала вида 1![]() 0 в системе входных процессов
0 в системе входных процессов ![]() , а M - общее число
изменения каждого вида.
, а M - общее число
изменения каждого вида.
Теорема 1 позволяет разбить время на
последовательные интервалы с постоянным числом
свободных входных импульсов (т.е. с постоянным
значением выходного сигнала y) в каждом
интервале. После этого для нахождения выходного
процесса асинхронной комбинационной схемы y(t)
остается лишь вычислить его значения в какой-то
одной точке каждого интервала. Указанное
разбиение времени на последовательные интервалы
дает в качестве границ интервалов моменты ![]() и
и ![]() начала и окончания свободных входных
импульсов схемы. Но из теоремы 1 следует, что
момент
начала и окончания свободных входных
импульсов схемы. Но из теоремы 1 следует, что
момент ![]() равен
логическому определителю
равен
логическому определителю ![]() ранга r от квазиматрицы
ранга r от квазиматрицы ![]() , где
, где ![]() - момент j-го
по порядку изменения сигнала вида 0
- момент j-го
по порядку изменения сигнала вида 0![]() 1 во входном процессе
1 во входном процессе ![]() на i-м входе схемы, аналогично момент
на i-м входе схемы, аналогично момент ![]() равен логическому
определителю
равен логическому
определителю ![]() ранга r от
квазиматрицы
ранга r от
квазиматрицы ![]() , где
, где ![]() - момент j-го по порядку
изменения сигнала вида 1
- момент j-го по порядку
изменения сигнала вида 1![]() 0
во входном процессе
0
во входном процессе ![]() на
i-м входе схемы. Таким образом, выходной процесс
любой асинхронной комбинационной схемы,
реализующей произвольную симметрическую булеву
логическую функцию своих входов, можно всегда
выразить с помощью логических определителей
на
i-м входе схемы. Таким образом, выходной процесс
любой асинхронной комбинационной схемы,
реализующей произвольную симметрическую булеву
логическую функцию своих входов, можно всегда
выразить с помощью логических определителей ![]() , различных рангов r от
квазиматрицы
, различных рангов r от
квазиматрицы ![]() моментов
всех изменений сигнала вида 0
моментов
всех изменений сигнала вида 0![]() 1 во всех входных процессах схемы и
квазиматрицы
1 во всех входных процессах схемы и
квазиматрицы ![]() моментов
всех изменений сигнала вида 1
моментов
всех изменений сигнала вида 1![]() 0 в указанных процессах.
0 в указанных процессах.
Рассмотрим конечный динамический
автомат без памяти, реализованный в виде
асинхронной комбинационной схемы с произвольным
числом входов n и одним выходом, на котором
реализуется базовая симметрическая булева
логическая функция входов ![]() некоторого индекса r. В этом случае по
определению данной функции значения входов
схемы
некоторого индекса r. В этом случае по
определению данной функции значения входов
схемы ![]() и ее выхода y
связаны соотношением
и ее выхода y
связаны соотношением
 (5)
(5)
Пусть на входы рассматриваемой схемы
действуют произвольные двоичные процессы ![]() в виде следующих
последовательностей импульсов 1(
в виде следующих
последовательностей импульсов 1(![]() ) в интервалах (
) в интервалах (![]() ) и промежуточных пауз 0(
) и промежуточных пауз 0(![]() ) между импульсами
) между импульсами
![]() . (6)
. (6)
Тогда на выходе этой схемы появится следующий двоичный процесс, также имеющий вид последовательности импульсов и пауз
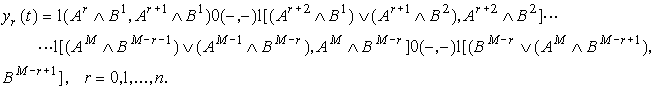 (7)
(7)
В формуле (7) ![]() -
указанные выше характеристические логические
определители различных рангов m, характеризующие
входные воздействия схемы (6),
-
указанные выше характеристические логические
определители различных рангов m, характеризующие
входные воздействия схемы (6), ![]() и
и ![]() - операции
дизъюнкции и конъюнкции непрерывной логики,
- операции
дизъюнкции и конъюнкции непрерывной логики, 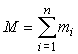 общее число импульсов во
всех входных воздействиях. Как видно из (7), общее
число импульсов в реакции схемы с реализуемой
функцией
общее число импульсов во
всех входных воздействиях. Как видно из (7), общее
число импульсов в реакции схемы с реализуемой
функцией ![]() на входные
воздействия (6) в общем случае равно M-r+1.
на входные
воздействия (6) в общем случае равно M-r+1.
5. Автоматная модель потока исторических событий
Применим теперь описанную в пп. 3,4
математическую модель конечного динамического
автомата без памяти для математического
моделирования потока исторических событий в
рамках задачи, поставленной в п.2. Для нахождения
различных количественных характеристик
суммарного потока событий поставим во
взаимно-однозначное соответствие заданному
потоку событий в любом i-м регионе двоичный
процесс-индикатор x![]() (t),
i=1,...,n, где переменная x
(t),
i=1,...,n, где переменная x![]() =1 означает наличие события в i-м регионе
в соответствующий момент времени t, а x
=1 означает наличие события в i-м регионе
в соответствующий момент времени t, а x![]() =0 - его отсутствие.
Аналогично, изучаемый суммарный поток событий
исчерпывающе характеризуется набором двоичных
процессов-индикаторов y
=0 - его отсутствие.
Аналогично, изучаемый суммарный поток событий
исчерпывающе характеризуется набором двоичных
процессов-индикаторов y![]() (t), s=0,1,...,n, где переменная y
(t), s=0,1,...,n, где переменная y![]() =1 означает, что
суммарный поток событий в данный момент времени t
содержит s одновременно происходящих событий, а y
=1 означает, что
суммарный поток событий в данный момент времени t
содержит s одновременно происходящих событий, а y![]() =0 - что суммарный поток в
этот момент содержит другое, отличное от s, число
одновременно происходящих событий. Двоичные
процессы y
=0 - что суммарный поток в
этот момент содержит другое, отличное от s, число
одновременно происходящих событий. Двоичные
процессы y![]() (t)
естественно называть спектральными временными
функциями суммарного потока событий, поскольку
временные интервалы их единичных значений - это
интервалы, в которых суммарный поток событий
содержит определенное число s одновременно
происходящих событий. Вектор-функцию
(t)
естественно называть спектральными временными
функциями суммарного потока событий, поскольку
временные интервалы их единичных значений - это
интервалы, в которых суммарный поток событий
содержит определенное число s одновременно
происходящих событий. Вектор-функцию ![]() , состоящий из всех
спектральных функций, назовем спектром
суммарного потока событий. Спектр обладает
свойством ортогональности
, состоящий из всех
спектральных функций, назовем спектром
суммарного потока событий. Спектр обладает
свойством ортогональности ![]()
![]()
![]() =0 при p
=0 при p![]() q.
Более того, в любой момент времени t из n+1
слагаемых спектральных функций y
q.
Более того, в любой момент времени t из n+1
слагаемых спектральных функций y![]() (t) только одна равна 1, а все
остальные равны 0.
(t) только одна равна 1, а все
остальные равны 0.
Кроме спектра, суммарный поток событий можно исчерпывающе охарактеризовать (n+1)-ичной функцией потока y(t), принимающей значения 0,1,...,n, причем y=к означает, что суммарный поток в данный момент времени t содержит к одновременно происходящих событий. Причем оба способа количественного описания суммарного потока событий эквиваленты. Так что по спектру можно всегда вычислить функцию потока, воспользовавшись очевидной формулой
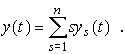 (8)
(8)
В свою очередь, имея функцию потока, всегда можно вычислить его спектр. Для этого служит следующая формула, вытекающая из определения спектра
 (9)
(9)
Итак, для исчерпывающего описания
суммарного потока событий достаточно определить
либо его спектр, либо его функцию потока. Мы
выберем первое. Для определения спектра ![]() суммарного потока
событий построим соответствующую автоматную
модель. Прежде всего, учтем, что согласно условию
задачи в любом i-м регионе в любой момент времени
может совершаться только одно интересующее нас
событие, либо не совершаться ни одного события.
Поэтому для того, чтобы в любой взятый момент
времени суммарный поток от всех n регионов
содержал s одновременно происходящих событий,
необходимо и достаточно, чтобы ровно в s из n
регионов в этот момент происходило это событие.
Отсюда следует, что зависимость неизвестных
двоичных переменных состояния изучаемой системы
суммарного потока
событий построим соответствующую автоматную
модель. Прежде всего, учтем, что согласно условию
задачи в любом i-м регионе в любой момент времени
может совершаться только одно интересующее нас
событие, либо не совершаться ни одного события.
Поэтому для того, чтобы в любой взятый момент
времени суммарный поток от всех n регионов
содержал s одновременно происходящих событий,
необходимо и достаточно, чтобы ровно в s из n
регионов в этот момент происходило это событие.
Отсюда следует, что зависимость неизвестных
двоичных переменных состояния изучаемой системы
![]() от заданных двоичных
переменных состояния регионов
от заданных двоичных
переменных состояния регионов ![]() можно выразить посредством
симметрических булевых логических функций
можно выразить посредством
симметрических булевых логических функций ![]() вида (5)
вида (5)
y![]() (t) =
(t) = ![]() (
(![]() ),
s=0,1,...,n,
),
s=0,1,...,n, ![]() . (10)
. (10)
Набор булевых логических функций
состояния изучаемой системы (10) есть
математическая модель этой системы. Как следует
из п.3, построенная модель представляет собой
некоторый конечный динамический автомат без
памяти, реализуемый в виде соответствующей
асинхронной комбинационной схемы с n входами и n+1
выходами (рис.1). На входы этой схемы-модели
подаются заданные двоичные процессы-индикаторы ![]() , моделирующие известное
распределение во времени исторических событий в
соответствующих регионах 1,...,n, а с выходов
снимаются подлежащие определению двоичные
спектральные функции
, моделирующие известное
распределение во времени исторических событий в
соответствующих регионах 1,...,n, а с выходов
снимаются подлежащие определению двоичные
спектральные функции ![]() искомого
суммарного потока событий y(t), по которым с
помощью формулы (8) можно определить и сам поток.
искомого
суммарного потока событий y(t), по которым с
помощью формулы (8) можно определить и сам поток.
6. Вычисление потока исторических событий по его автоматной модели
В соответствии с построенной в п.5
автоматной моделью системы, формирующей искомый
суммарный поток исторических событий,
поставленная задача определения двоичных
процессов ![]() -
спектральных функций искомого суммарного потока
событий, по известным двоичным процессам
-
спектральных функций искомого суммарного потока
событий, по известным двоичным процессам ![]() , задающим потоки
исторических событий в соответствующих
регионах, сводится к стандартной задаче
динамической теории автоматов - расчету
динамических процессов
, задающим потоки
исторических событий в соответствующих
регионах, сводится к стандартной задаче
динамической теории автоматов - расчету
динамических процессов ![]() на выходах конечного динамического
автомата без памяти - модели нашей системы, по
построенной асинхронной комбинационной схеме,
реализующей этот автомат (рис.1), и заданным
входным процессам этой схемы
на выходах конечного динамического
автомата без памяти - модели нашей системы, по
построенной асинхронной комбинационной схеме,
реализующей этот автомат (рис.1), и заданным
входным процессам этой схемы ![]() . Последние, как следует из постановки
задачи (п.2) имеют вид (6). Эту задачу решаем методом
подстановок (п.3). Шаг 1, предусмотренный методом,
здесь не требуется, т.к. схема содержит только
одну ступень. Шаг 2 уже выполнен в п.4, где найдены
соотношения (7) между входными и выходными
процессами типовых элементов с реализуемыми
булевыми логическими функциями
. Последние, как следует из постановки
задачи (п.2) имеют вид (6). Эту задачу решаем методом
подстановок (п.3). Шаг 1, предусмотренный методом,
здесь не требуется, т.к. схема содержит только
одну ступень. Шаг 2 уже выполнен в п.4, где найдены
соотношения (7) между входными и выходными
процессами типовых элементов с реализуемыми
булевыми логическими функциями ![]() , r=0,1,...,n составляющих схему
рис.1. Остается выполнить шаг 3, для чего
достаточно в соотношениях (7) последовательно
положить r=0,1,2,...,n и произвести необходимые
упрощения в получаемых выражениях выходных
динамических процессов
, r=0,1,...,n составляющих схему
рис.1. Остается выполнить шаг 3, для чего
достаточно в соотношениях (7) последовательно
положить r=0,1,2,...,n и произвести необходимые
упрощения в получаемых выражениях выходных
динамических процессов ![]() , учитывая простейшие общие свойства
операций непрерывной логики и логических
определителей
, учитывая простейшие общие свойства
операций непрерывной логики и логических
определителей ![]()
![]() , при
, при ![]() . (11)
. (11)
В результате получим следующие
выражения указанных процессов в виде
последовательностей импульсов 1(![]() ) в интервалах (
) в интервалах (![]() ) и промежуточных пауз 0(
) и промежуточных пауз 0(![]() ) между импульсами:
) между импульсами:
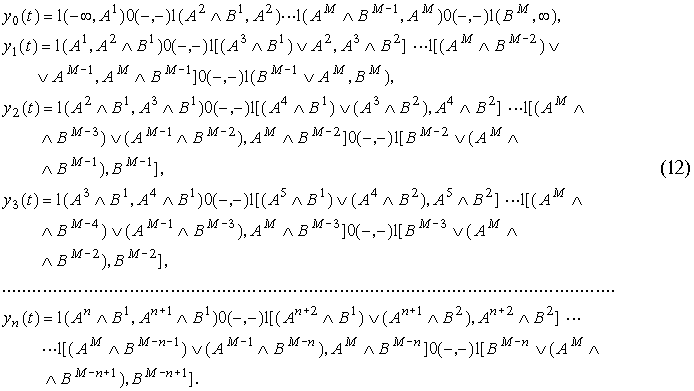
В выражениях (12) ![]() - введенные в п.4 характеристические
логические определители различных рангов r,
характеризующие входные воздействия
- введенные в п.4 характеристические
логические определители различных рангов r,
характеризующие входные воздействия ![]() вида (6) схемы рис.1,
вида (6) схемы рис.1, ![]() и
и ![]() - операции дизъюнкции и конъюнкции
непрерывной логики,
- операции дизъюнкции и конъюнкции
непрерывной логики, 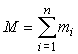 -
общее число импульсов во всех входных
воздействиях, т.е. общее число событий со всех
регионах. В терминах изучаемых исторических
событий
-
общее число импульсов во всех входных
воздействиях, т.е. общее число событий со всех
регионах. В терминах изучаемых исторических
событий ![]() означает
момент начала j-го по порядку события в i-м
регионе,
означает
момент начала j-го по порядку события в i-м
регионе, ![]() - означает
момент его окончания,
- означает
момент его окончания, ![]() -
число событий в i-м регионе,
-
число событий в i-м регионе, 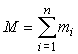 - общее число событий во всех регионах.
- общее число событий во всех регионах.
Полученные выражения (12) выходных
динамических процессов ![]() автомата-модели суммарного потока
исторических событий дают полное решение
поставленной в п.2 задачи количественного
изучения этого потока. А именно, интервалы
времени, в которых произвольный выходной процесс
автомата-модели суммарного потока
исторических событий дают полное решение
поставленной в п.2 задачи количественного
изучения этого потока. А именно, интервалы
времени, в которых произвольный выходной процесс
![]() , s=0,1,...,n, равен 1, есть
именно те интервалы, в которых суммарный поток
событий содержит ровно s одновременно
происходящих событий - по одному в каждом из s
каких-то регионов. Таким образом, зная эти
процессы, можно определять любые количественные
характеристики суммарного потока событий. В
частности, по найденным процессам можно с
помощью формулы (8) вычислить функцию потока y(t).
Возможно также нахождение любых других
количественных характеристик этого потока.
Важнейшими из них являются, по-видимому,
характеристики временной плотности суммарного
потока событий. Введем эти характеристики
суммарного потока событий в виде двух семейств
векторов: векторов
, s=0,1,...,n, равен 1, есть
именно те интервалы, в которых суммарный поток
событий содержит ровно s одновременно
происходящих событий - по одному в каждом из s
каких-то регионов. Таким образом, зная эти
процессы, можно определять любые количественные
характеристики суммарного потока событий. В
частности, по найденным процессам можно с
помощью формулы (8) вычислить функцию потока y(t).
Возможно также нахождение любых других
количественных характеристик этого потока.
Важнейшими из них являются, по-видимому,
характеристики временной плотности суммарного
потока событий. Введем эти характеристики
суммарного потока событий в виде двух семейств
векторов: векторов ![]() моментов
начала и векторов
моментов
начала и векторов ![]() моментов
окончания интервалов с постоянным числом s
происходящих событий (т.е. с постоянной
плотностью s). При этом вектор
моментов
окончания интервалов с постоянным числом s
происходящих событий (т.е. с постоянной
плотностью s). При этом вектор
![]() (13)
(13)
В (13) ![]() означает
момент начала очередного i-го по порядку
интервала времени, в котором суммарный поток
событий имеет плотность s, т.е. содержит ровно s
одновременно происходящих событий. Аналогично
вектор
означает
момент начала очередного i-го по порядку
интервала времени, в котором суммарный поток
событий имеет плотность s, т.е. содержит ровно s
одновременно происходящих событий. Аналогично
вектор
![]() (14)
(14)
В (14) ![]() означает
момент окончания очередного i-го по порядку,
интервала времени, в котором суммарный поток
событий имеет плотность s, т.е. содержит ровно s
одновременно происходящих событий. Для
нахождения семейств векторов моментов начала и
моментов окончания интервалов постоянной
плотности суммарного потока событий достаточно
учесть, что момент начала (окончания) i-го по
порядку интервала времени, в котором суммарный
поток событий содержит ровно s одновременно
происходящих событий, есть момент начала
(окончания) i-го по порядку импульса в выходном
динамическом процессе
означает
момент окончания очередного i-го по порядку,
интервала времени, в котором суммарный поток
событий имеет плотность s, т.е. содержит ровно s
одновременно происходящих событий. Для
нахождения семейств векторов моментов начала и
моментов окончания интервалов постоянной
плотности суммарного потока событий достаточно
учесть, что момент начала (окончания) i-го по
порядку интервала времени, в котором суммарный
поток событий содержит ровно s одновременно
происходящих событий, есть момент начала
(окончания) i-го по порядку импульса в выходном
динамическом процессе ![]() автомата-модели
системы (рис.1). Используя теперь выражения (12)
процессов
автомата-модели
системы (рис.1). Используя теперь выражения (12)
процессов ![]() , где явно
даны моменты начала и окончания всех импульсов,
получим явные выражения характеристик временной
плотности суммарного потока событий
, где явно
даны моменты начала и окончания всех импульсов,
получим явные выражения характеристик временной
плотности суммарного потока событий
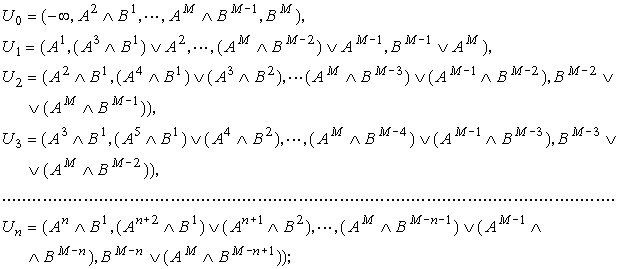 (15)
(15)
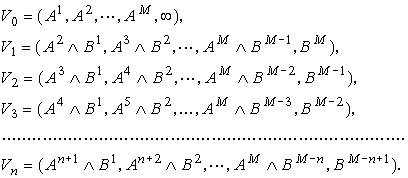 (16)
(16)
Из характеристик временной плотности
суммарного потока событий в виде векторов ![]() (15) моментов начала и
векторов
(15) моментов начала и
векторов ![]() (16) моментов
окончания интервалов постоянной плотности s
этого потока можно получить другую
характеристику временной плотности указанного
потока - длительности интервалов постоянной
плотности потока. Введем данную характеристику в
виде семейства векторов
(16) моментов
окончания интервалов постоянной плотности s
этого потока можно получить другую
характеристику временной плотности указанного
потока - длительности интервалов постоянной
плотности потока. Введем данную характеристику в
виде семейства векторов ![]() длительности интервалов постоянной
плотности s, т.е. интервалов, содержащих то или
иное фиксированное число s одновременно
происходящих событий. При этом вектор,
длительности интервалов постоянной
плотности s, т.е. интервалов, содержащих то или
иное фиксированное число s одновременно
происходящих событий. При этом вектор,
![]() (17)
(17)
где ![]() означает
длительность очередного i-го по порядку
интервала времени, в котором суммарный поток
событий содержит ровно s одновременно
происходящих событий. Ясно, что
означает
длительность очередного i-го по порядку
интервала времени, в котором суммарный поток
событий содержит ровно s одновременно
происходящих событий. Ясно, что
![]()
![]() , (18)
, (18)
где ![]() - моменты
начала вычисляемых интервалов, являющиеся
соответствующими i-ми элементами векторов
- моменты
начала вычисляемых интервалов, являющиеся
соответствующими i-ми элементами векторов ![]() (формула (15)), а
(формула (15)), а ![]() - моменты окончания этих
интервалов, являющиеся i-ми элементами векторов
- моменты окончания этих
интервалов, являющиеся i-ми элементами векторов ![]() (формула (16)).
(формула (16)).
Совмещая характеристики ![]() ,
, ![]() и
и ![]() , получим сводную
характеристику временной плотности суммарного
потока событий в виде векторов
, получим сводную
характеристику временной плотности суммарного
потока событий в виде векторов ![]() - координат интервалов постоянной
плотности s потока и длительности этих
интервалов. При этом новая характеристика
представляется в виде векторов
- координат интервалов постоянной
плотности s потока и длительности этих
интервалов. При этом новая характеристика
представляется в виде векторов
![]() (19)
(19)
каждый i-й элемент которых содержит i-й
интервал ![]() постоянной
плотности s суммарного потока событий, т.е.
моменты начала
постоянной
плотности s суммарного потока событий, т.е.
моменты начала ![]() и
окончания
и
окончания ![]() этого
интервала и длительности этого интервала
этого
интервала и длительности этого интервала ![]() .
.
Исходя из рассмотренных выше
абсолютных характеристик суммарного потока
событий, можно определить ряд относительных и
усредненных характеристик. В первую очередь это
доля времени ![]() , в течение
которой плотность (число одновременно
происходящих событий) суммарного потока событий
равна данной фиксированной величине
, в течение
которой плотность (число одновременно
происходящих событий) суммарного потока событий
равна данной фиксированной величине ![]() ,
, ![]() =0,1,...,n,
а также среднее число
=0,1,...,n,
а также среднее число ![]() одновременно
происходящих событий за изучаемый период
времени. Введенные характеристики вычисляются
по формулам
одновременно
происходящих событий за изучаемый период
времени. Введенные характеристики вычисляются
по формулам
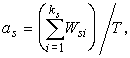 (20)
(20)
где ![]() берутся из (17)-(19), а
берутся из (17)-(19), а
![]() - длительность
изучаемого периода времени, равная
- длительность
изучаемого периода времени, равная
![]() (21)
(21)
где ![]() ,
, ![]() берутся из (19), а
берутся из (19), а ![]() и
и ![]() - операции
дизъюнкции и конъюнкции непрерывной логики
(см.п.3)
- операции
дизъюнкции и конъюнкции непрерывной логики
(см.п.3)
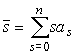 , (22)
, (22)
7. Иллюстративный пример
В стране Асолия постоянно неспокойно - три ее провинции: Юго-Восточную, Восточную и Северо-Восточную периодически потрясают восстания, с трудом подавляемые центральными властями. За последние 50 лет таких восстаний было 9. Они продолжались 1) в Юго-Восточной провинции с 2050-го до 2058-го, затем с 2067-го до 2079-го и, наконец, с 2088-го до 2100-го года, 2) в Восточной провинции с 2054-го до 2062-го, с 2070-го до 2077-го и с 2082-го до 2093-го года, 3) В Северо-Восточной провинции с 2052-го до 2061-го, с 2065-го до 2074-го и с 2085-го до 2096-го года. Вычислим и проанализируем суммарный поток восстаний в стране Асолия.
Используем формулы частот суммарного
потока (15) и формулы его длительностей (16). Для
этого вычислим сначала входящие в эти формулы
логические определители ![]() ,
, ![]() различных
рангов p от квазиматриц
различных
рангов p от квазиматриц ![]() и
и
![]() . Эти квазиматрицы
состоят из моментов начала
. Эти квазиматрицы
состоят из моментов начала ![]() и окончания
и окончания ![]() восстаний
j в провинциях i и при выше принятой нумерации
провинций имеют вид
восстаний
j в провинциях i и при выше принятой нумерации
провинций имеют вид
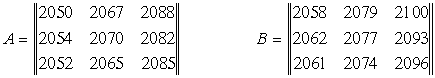
Теперь логические определители ![]() ,
, ![]() находим
как p-е по возрастанию элементы соответствующих
квазиматриц
находим
как p-е по возрастанию элементы соответствующих
квазиматриц
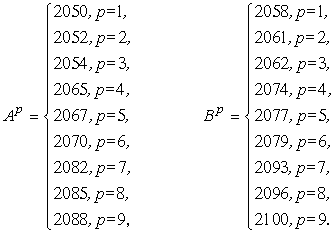
Отсюда, учитывая, что в нашем случае
число регионов (провинций) n=3, число событий
(восстаний) в них m1= m2= m3=3, общее
число событий 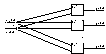 , по формулам (15) находим векторы
, по формулам (15) находим векторы ![]() моментов начала
интервалов постоянной плотности s суммарного
потока восстаний
моментов начала
интервалов постоянной плотности s суммарного
потока восстаний
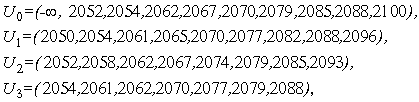
и по формулам (16) - векторы ![]() моментов окончания этих интервалов
моментов окончания этих интервалов

Наконец, по формулам (17),(18) находим векторы ![]() длительностей интервалов
постоянной плотности s в суммарном потоке
восстаний
длительностей интервалов
постоянной плотности s в суммарном потоке
восстаний
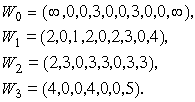
Совместив характеристики ![]() ,
, ![]() и
и ![]() , согласно формуле (19), получим
сводную характеристику временной плотности
суммарного потока восстаний
, согласно формуле (19), получим
сводную характеристику временной плотности
суммарного потока восстаний

или после исключения вырожденных
интервалов (![]() ,
,![]() ), т.е. интервалов с
совпадающими моментами начала
), т.е. интервалов с
совпадающими моментами начала ![]() и конца
и конца ![]() и
нулевой длительностью
и
нулевой длительностью ![]() ,
,
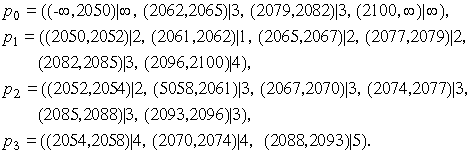
Как следует из полученных выражений, в стране
Асолия за последние Т=50 лет- с 2050-го до 2100-го гг. -
лишь на протяжении двух интервалов времени: с
2062-го до 2065-го и с 2079-го до 2082-го гг., каждый
длительностью 3 года (общая длительность 6 лет), не
было ни одного восстания; в то же время на
протяжении 6 интервалов, длительностью
соответственно 2, 1, 2, 2, 3, 4 лет (общая длительность
14 лет) в стране происходило одно восстание, на
протяжении 6 интервалов, длительностью
соответственно 2,,3, 3, 3, 3, 3 года (общая
длительность 17 лет), происходило одновременно
два восстания, на протяжении 3 интервалов,
длительностью соответственно 4,4,5 лет (общая
длительность 13 лет), происходило одновременно 3
восстания. Таким образом, доля времени ![]() с плотностью (числом
одновременно происходящих) восстаний s по
формуле (20) равна
с плотностью (числом
одновременно происходящих) восстаний s по
формуле (20) равна
![]()
Среднее число одновременно происходящих восстаний за изучаемый период времени согласно формуле (22) равно
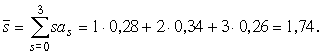
Вычислим еще функцию потока восстаний y(t). По
формуле (8), учитывая, что спектральные функции ![]() в рассматриваемом примере
выражаются векторами
в рассматриваемом примере
выражаются векторами ![]() ,
получим таблицу значений y(t) (табл.1)
,
получим таблицу значений y(t) (табл.1)
Таблица 1
Интервалы времени t |
( 2050) |
(2050, 2052) |
(2052, 2064) |
(2054, 2058) |
(2058, 2061) |
(2061, 2062) |
|||||||||||
Значения y(t) |
0 |
1 |
2 |
3 |
2 |
1 |
|||||||||||
(2062, 2065) |
(2065, 2067) |
(2067, 2070) |
(2070, 2074) |
(2074, 2077) |
(2077, 2079) |
(2079, 2082) |
(2082, 2085) |
(2085, 2088) |
|||||||||
0 |
1 |
2 |
3 |
2 |
1 |
0 |
1 |
2 |
|||||||||
(2088, 2093) |
(2093, 2096) |
(2096, 2100) |
(2100,
|
||||||||||||||
3 |
2 |
1 |
0 |
||||||||||||||
Соответствующий график функции y(t) показан на рис.2.
Итак, лишь на протяжении 12% от рассматриваемого 50-летнего периода времени в стране Асолия спокойно , зато на протяжении 88% этого времени в ней происходят восстания - в среднем 1,74 восстания одновременно. При этом плотность восстаний периодически становится максимально возможной (рис.1). Такую ситуацию естественно считать весьма неустойчивой.
8. Заключение
Предложенная новая математическая модель потока однородных исторических событий - динамический конечный автомат, совместно с адекватным математическим аппаратом изучения динамических автоматов - непрерывной логикой и логическими определителями - позволяет выполнять в символической форме расчет разнообразных количественных характеристик потока. Это открывает возможность детального анализа временных закономерностей появления новых событий. Целесообразно в будущем использовать предложенную модель для прогнозирования моментов возникновения новых событий. Интересно и важно также распространить эту модель на случаи возможности неопределенных состояний исторического процесса, промежуточных между наступлением и ненаступлением исторического события.
Литература
AUTOMATON MODELING OF FLOW OF HISTORY EVENTS
V. I. Levin
Considered problem of mathematical modeling total flow of uniform history events, got summation similar regional flows. Incorporated different features of prototyping flow of events. Shown possibility modeling of flows by means of the dynamic automaton memoryless. Herewith regional flows of events are prototyped entry-ными processes of automaton-models, total flow of events - its output process, but correlation of regional and total lived for a flows - a logical function of automaton. Built model allows to analyse a total flow of history events by methods analytical speakers of end automatons.
Поступила в редакцию 27.07.2001.