УДК 519.1
ДИНАМИЧЕСКИЙ АВТОМАТ И МОДЕЛИРОВАНИЕ ДИНАМИКИ СОЦИАЛЬНЫХ ГРУПП
© 2001 г. В. И. Левин
Изложена новая модель динамического
поведения социальной группы - динамический
конечный автомат. В ней динамика поведения ![]() -го индивидуума
моделируется процессом на
-го индивидуума
моделируется процессом на ![]() -м входе автомата, динамика поведения всей
группы - процессом на его выходе, а статическая
зависимость состояния группы от состояний
индивидуумов - булевой логической функцией
автомата. Для количественного изучения модели
предложены методы современной теории
динамических автоматов, основанные на
математическом аппарате непрерывной логики, что
позволяет получать результаты в символической
форме.
-м входе автомата, динамика поведения всей
группы - процессом на его выходе, а статическая
зависимость состояния группы от состояний
индивидуумов - булевой логической функцией
автомата. Для количественного изучения модели
предложены методы современной теории
динамических автоматов, основанные на
математическом аппарате непрерывной логики, что
позволяет получать результаты в символической
форме.
1. Введение
Вот уже в течение нескольких десятилетий специалисты по математической социологии используют для количественного изучения поведения групп индивидуумов различные математические модели. Подавляющая часть этих моделей описывает статику или установившееся (предельное) поведение группы и относится к одному из трех классов: 1) вероятностные марковские модели [1]; 2) модели, основанные на использовании линейной алгебры [2]; 3) графовые модели [1,3]. В то же время, по нашему мнению, более важной и интересной частью математической социологии (точнее, социальной психологии) является изучение динамики поведения групп, т.е. изменения во времени структуры и/или характера взаимоотношений между индивидуумами внутри группы и, как следствие, - изменения состояния группы в целом. Для решения этой задачи вторая и третья из названных моделей принципиально непригодны. Первая модель, которая в принципе могла бы быть использована, требует большого объема исходных статистических данных, затраты на получение которых мало оправданы. Действительно, использование любой вероятностной модели предполагает постоянство условий, при которых определяются различные вероятности, однако человек таким постоянством не обладает. В настоящей работе предлагается новая математическая модель для описания динамики поведения групп - динамический конечный автомат [4-6]. В ней автомат-модель имеет число входов, равное числу индивидуумов, и один выход и реализует логическую функцию, соответствующую заданной статической зависимости между состояниями индивидуумов, и состоянием группы в целом в один и тот же произвольный момент времени. При этом на входы автомата поступают процессы, моделирующие известные изменения во времени состояний индивидуумов, а с выхода снимается искомый процесс изменения во времени состояния группы. Таким образом, расчет и анализ динамического поведения группы сводится к расчету и анализу выходного процесса автомата-модели по заданным входным процессам. Задачи же расчета и анализа процессов в динамических автоматах детально разработаны автором в созданной им теории динамических автоматов [4-6], в которой для решения этих и других задач предложен адекватный математический аппарат непрерывной логики (НЛ) и ее многомерное обобщение - логические определители (ЛО). Таким образом, предлагаемая адекватная математическая модель позволяет количественно в символической форме изучать временное поведение групп с помощью адекватного математического аппарата НЛ (для малых групп) или ЛО (для больших групп).
2. Постановка задачи
Рассмотрим произвольную социальную
группу, состоящую из n индивидуумов. Каждый
индивидуум в любой момент времени может
находиться только в одном из двух состояний:
работоспособном или неработоспособном.
Работоспособное состояние индивидуума означает
его способность быть полноценным членом группы,
т.е. участвовать в ее работе в полном
соответствии со своей индивидуальной
спецификацией (перечнем обязательных
выполняемых действий). Неработоспособное
состояние индивидуума означает его
неспособность быть полноценным членом группы,
вследствие фактического неучастия в ее работе -
невыполнения своей индивидуальной спецификации.
Примеры неработоспособного состояния
индивидуума - пребывание в отпуске, в состоянии
болезни, а также нахождение в состоянии
конфликта с другими индивидуумами и вследствие
этого отказа от выполнения спецификации и т.д.
Аналогично вводятся состояния группы в целом:
группа в любой момент ![]() может
находиться только в одном из двух состояний:
работоспособном или неработоспособном.
Работоспособное состояние группы означает ее
пригодность к выполнению определенного
группового задания, в соответствии с чем группа
должна иметь достаточно высокий уровень
определенных количественных характеристик,
например, стабильности или надежности или
суммарной производительности и т.д.
Неработоспособное состояние группы означает ее
непригодность к выполнению предписанного
группового задания, вследствие недостаточного
уровня необходимых для этого количественных
характеристик. Состояние группы в произвольный
момент времени t, согласно нашему предположению,
полностью определяется состояниями всех ее
индивидуумов в этот момент. Эта зависимость
состояния группы от состояний всех ее
индивидуумов одна и та же для любых
может
находиться только в одном из двух состояний:
работоспособном или неработоспособном.
Работоспособное состояние группы означает ее
пригодность к выполнению определенного
группового задания, в соответствии с чем группа
должна иметь достаточно высокий уровень
определенных количественных характеристик,
например, стабильности или надежности или
суммарной производительности и т.д.
Неработоспособное состояние группы означает ее
непригодность к выполнению предписанного
группового задания, вследствие недостаточного
уровня необходимых для этого количественных
характеристик. Состояние группы в произвольный
момент времени t, согласно нашему предположению,
полностью определяется состояниями всех ее
индивидуумов в этот момент. Эта зависимость
состояния группы от состояний всех ее
индивидуумов одна и та же для любых ![]() . Она является (при неизменности
состояний индивидуумов) моделью статического
поведения группы и считается заданной. Также
считаем заданными динамику изменения состояния
всех индивидуумов во времени. Задача состоит в
том, чтобы определить соответствующую динамику
изменения состояния всей группы во времени.
. Она является (при неизменности
состояний индивидуумов) моделью статического
поведения группы и считается заданной. Также
считаем заданными динамику изменения состояния
всех индивидуумов во времени. Задача состоит в
том, чтобы определить соответствующую динамику
изменения состояния всей группы во времени.
3. Автоматная модель группового поведения
В соответствии с описанием заданной группы (п.2)
математическую модель ее динамического
поведения можно построить следующим образом.
Поставим во взаимно-однозначное соответствие
работоспособному состоянию любого индивидуума
значение 1, а его неработоспособному состоянию -
значение 0. Аналогично закодируем
работоспособное и неработоспособное состояние
всей группы. Обозначим состояние ![]() -го индивидуума
-го индивидуума ![]() , а состояние группы переменной
, а состояние группы переменной ![]() . Ясно, что в любой момент
времени
. Ясно, что в любой момент
времени ![]() и
и ![]() . Причем равенство
. Причем равенство ![]() означает, что в этот
означает, что в этот ![]() -й индивидуум находится в
работоспособном (неработоспособном) состоянии.
Таким образом, заданной динамике изменения
состояния произвольного
-й индивидуум находится в
работоспособном (неработоспособном) состоянии.
Таким образом, заданной динамике изменения
состояния произвольного ![]() -го индивидуума можно поставить во
взаимно-однозначное соответствие двоичный
процесс
-го индивидуума можно поставить во
взаимно-однозначное соответствие двоичный
процесс ![]() , где
, где ![]() . Аналогично искомой
динамике изменения состояния группы можно
поставить во взаимно-однозначное соответствие
двоичный процесс
. Аналогично искомой
динамике изменения состояния группы можно
поставить во взаимно-однозначное соответствие
двоичный процесс ![]() .
Далее, заданная модель статического поведения
группы (§ 2) показывает однозначную зависимость
состояния группы
.
Далее, заданная модель статического поведения
группы (§ 2) показывает однозначную зависимость
состояния группы ![]() y от
состояний всех ее индивидуумов
y от
состояний всех ее индивидуумов ![]() не изменяющуюся со временем. Таким
образом, учитывая двоичный характер переменных
не изменяющуюся со временем. Таким
образом, учитывая двоичный характер переменных ![]() модель статического
поведения группы можно задать двоичной
логической (т.е. булевой) функцией состояния
группы
модель статического
поведения группы можно задать двоичной
логической (т.е. булевой) функцией состояния
группы
![]() . (1)
. (1)
Функция состояния (1) является формальным
выражением указанной выше однозначной
зависимости состояния группы y от состояний всех
ее индивидуумов ![]() , общей
для всех моментов времени. Данная модель
предполагает, что переменные
, общей
для всех моментов времени. Данная модель
предполагает, что переменные ![]() (и, как следствие, переменная
(и, как следствие, переменная ![]() ) не изменяется во времени. Модель
динамического поведения группы отличается от
введенной модели ее статического поведения тем,
что независимые
) не изменяется во времени. Модель
динамического поведения группы отличается от
введенной модели ее статического поведения тем,
что независимые ![]() и
зависимая
и
зависимая ![]() переменные
функции (1) изменяются во времени, принимая вид
соответствующих процессов
переменные
функции (1) изменяются во времени, принимая вид
соответствующих процессов ![]() и
и ![]() . Таким образом,
в отличие от модели поведения группы в статике,
где базовой задачей является нахождение с
помощью известной функции состояния (1) по
известным состояниям индивидуумов
. Таким образом,
в отличие от модели поведения группы в статике,
где базовой задачей является нахождение с
помощью известной функции состояния (1) по
известным состояниям индивидуумов ![]() , неизвестного состояния группы
, неизвестного состояния группы ![]() , в модели динамического
поведения группы базовой задачей становится
нахождение с помощью известной функции
состояния (1) по известным про-цессам изменения
состояния индивидуумов
, в модели динамического
поведения группы базовой задачей становится
нахождение с помощью известной функции
состояния (1) по известным про-цессам изменения
состояния индивидуумов ![]() ,
неизвестного процесса изменения состояния
группы
,
неизвестного процесса изменения состояния
группы ![]() . Вторая задача
не сводится к первой, а принципиально сложнее ее.
Действительно, такое сведение потребовало бы
решения первой задачи для любого момента времени
из континуального множества моментов шкалы
непрерывного времени, что невозможно. Выход из
этой принципиальной сложности можно найти,
сформулировав построенные модели статического и
динамического поведения группы в терминах
современной теории конечных автоматов [4-7] (в
частности, для моделей динамического поведения -
в терминах теории динамических автоматов [4-6]).
. Вторая задача
не сводится к первой, а принципиально сложнее ее.
Действительно, такое сведение потребовало бы
решения первой задачи для любого момента времени
из континуального множества моментов шкалы
непрерывного времени, что невозможно. Выход из
этой принципиальной сложности можно найти,
сформулировав построенные модели статического и
динамического поведения группы в терминах
современной теории конечных автоматов [4-7] (в
частности, для моделей динамического поведения -
в терминах теории динамических автоматов [4-6]).
Как известно [4-7], математическая модель (1) с
зависимостью в виде логической булевой функцией ![]() , преобразующей двоичные
переменные
, преобразующей двоичные
переменные ![]() в двоичную
переменную
в двоичную
переменную ![]() одинаково
для всех моментов времени (в предположении, что
переменные
одинаково
для всех моментов времени (в предположении, что
переменные ![]() , и как
следствие, переменная
, и как
следствие, переменная ![]() ,
не изменяются во времени), называется конечным
автоматом без памяти. Мы будем называть его также
статическим, подчеркивая этим независимость его
работы от времени. Сопоставляя содержательный
смысл модели (1), описывающей поведение группы в
статике, и указанную ее автоматную
интерпретацию, приходим к следующему выводу.
Математической моделью поведения группы в
статике является статический конечный автомат
без памяти, содержащий
,
не изменяются во времени), называется конечным
автоматом без памяти. Мы будем называть его также
статическим, подчеркивая этим независимость его
работы от времени. Сопоставляя содержательный
смысл модели (1), описывающей поведение группы в
статике, и указанную ее автоматную
интерпретацию, приходим к следующему выводу.
Математической моделью поведения группы в
статике является статический конечный автомат
без памяти, содержащий ![]() входов
(по числу индивидуумов в группе) и один выход и
реализующий на выходе булеву логическую функцию
(1) от входов, т.е. функцию состояния группы (рис.1).
При этом на входы автомата подаются двоичные
переменные
входов
(по числу индивидуумов в группе) и один выход и
реализующий на выходе булеву логическую функцию
(1) от входов, т.е. функцию состояния группы (рис.1).
При этом на входы автомата подаются двоичные
переменные ![]() , где
, где ![]() , моделирующие постоянные
состояния индивидуумов, а с выхода снимается
двоичная переменная
, моделирующие постоянные
состояния индивидуумов, а с выхода снимается
двоичная переменная ![]() ,
где
,
где ![]() , моделирующая
постоянное состояние группы. Данная модель
статического поведения группы является
абстрактной, поскольку она представлена в виде
устройства (рис.1) с известной реализуемой
функцией (1), но с неизвестной внутренней
структурой. Однако, в соответствии с теорией
конечных автоматов [4-7], это устройство можно
реализовать структурно в виде тех или иных
комбинационных логических схем, т.е. схем без
обратных связей, состоящих из соединенных между
собой логических элементов - простейших конечных
автоматов без памяти. Все эти схемы эквивалентны,
т.к. реализуют на выходе одну и ту же функцию
входов (1). При этом каждая схема с ее входными и
выходными переменными является структурной
моделью статического поведения группы. Отметим,
что описанная структура конечного автомата без
памяти, являющаяся структурной моделью
группового поведения в статике, никак не связана
со структурой взаимоотношений индивидуумов в
группе. Другими словами, построение структурной
схемы указанного автомата-модели является чисто
модельным построением, преследующим
единственную цель: удобства и простоты
моделирования поведения группы.
, моделирующая
постоянное состояние группы. Данная модель
статического поведения группы является
абстрактной, поскольку она представлена в виде
устройства (рис.1) с известной реализуемой
функцией (1), но с неизвестной внутренней
структурой. Однако, в соответствии с теорией
конечных автоматов [4-7], это устройство можно
реализовать структурно в виде тех или иных
комбинационных логических схем, т.е. схем без
обратных связей, состоящих из соединенных между
собой логических элементов - простейших конечных
автоматов без памяти. Все эти схемы эквивалентны,
т.к. реализуют на выходе одну и ту же функцию
входов (1). При этом каждая схема с ее входными и
выходными переменными является структурной
моделью статического поведения группы. Отметим,
что описанная структура конечного автомата без
памяти, являющаяся структурной моделью
группового поведения в статике, никак не связана
со структурой взаимоотношений индивидуумов в
группе. Другими словами, построение структурной
схемы указанного автомата-модели является чисто
модельным построением, преследующим
единственную цель: удобства и простоты
моделирования поведения группы.
Из теории динамических автоматов известно [4-6],
что математическая модель (1) с зависимостью в
виде булевой функцией ![]() ,
преобразующей двоичные входные процессы
,
преобразующей двоичные входные процессы ![]() в двоичный выходной
процесс
в двоичный выходной
процесс ![]() , является
динамическим автоматом без памяти. Сопоставляя
содержательный смысл модели (1) с входными
, является
динамическим автоматом без памяти. Сопоставляя
содержательный смысл модели (1) с входными ![]() и выходным
и выходным ![]() процессами, описывающей поведение
группы в динамике, и указанную автоматную
интерпретацию этой модели, получаем следующий
результат. Математической моделью поведения
группы в динамике является дина-мический автомат
без памяти, содержащий
процессами, описывающей поведение
группы в динамике, и указанную автоматную
интерпретацию этой модели, получаем следующий
результат. Математической моделью поведения
группы в динамике является дина-мический автомат
без памяти, содержащий ![]() входов
(по числу индивидуумов в этой группе) и один выход
и реализующий на выходе логическую булеву
функцию (1) от входов - функцию состояния группы
(рис.2). При этом на входы автомата подаются
двоичные процессы
входов
(по числу индивидуумов в этой группе) и один выход
и реализующий на выходе логическую булеву
функцию (1) от входов - функцию состояния группы
(рис.2). При этом на входы автомата подаются
двоичные процессы ![]() , где
, где ![]() , моделирующие изменение
во времени состояния индивидуумов, а с выхода
снимается двоичный процесс
, моделирующие изменение
во времени состояния индивидуумов, а с выхода
снимается двоичный процесс ![]() , где
, где ![]() ,
моделирующий изменение во времени состояния
группы. Построенная модель динамического
поведения группы (рис.2), как и модель ее
статического поведения (рис.1), является
абстрактной. При этом первая, как и вторая, может
быть реализована структурно в виде той или иной
комбинационной логической схемы, которая вместе
с ее входными и выходными процессами является
структурной моделью динамического поведения
группы. Заметим что, поскольку обе абстрактные
модели реализуют одну и ту же булеву логическую
функцию
,
моделирующий изменение во времени состояния
группы. Построенная модель динамического
поведения группы (рис.2), как и модель ее
статического поведения (рис.1), является
абстрактной. При этом первая, как и вторая, может
быть реализована структурно в виде той или иной
комбинационной логической схемы, которая вместе
с ее входными и выходными процессами является
структурной моделью динамического поведения
группы. Заметим что, поскольку обе абстрактные
модели реализуют одну и ту же булеву логическую
функцию ![]() , то любая
структурная схема, реализующая эту функцию и
потому пригодная в качестве структурной модели
статического поведения группы, пригодна также и
в качестве структурной модели ее динамического
поведения. Однако, несмотря на одинаковую
реализуемую функцию
, то любая
структурная схема, реализующая эту функцию и
потому пригодная в качестве структурной модели
статического поведения группы, пригодна также и
в качестве структурной модели ее динамического
поведения. Однако, несмотря на одинаковую
реализуемую функцию ![]() в
обеих абстрактных моделях и одинаковые
структурные схемы в обеих структурных моделях,
между ними имеется существенная разница,
определяющая принципиальное различие в
сложности их исследования, о чем уже сказано в
начале параграфа. А именно, автоматная модель
поведения группы в статике, как абстрактная
(рис.1), так и структурная, характеризуется
неизменностью поступающих на входы
автомата-модели входных переменных
в
обеих абстрактных моделях и одинаковые
структурные схемы в обеих структурных моделях,
между ними имеется существенная разница,
определяющая принципиальное различие в
сложности их исследования, о чем уже сказано в
начале параграфа. А именно, автоматная модель
поведения группы в статике, как абстрактная
(рис.1), так и структурная, характеризуется
неизменностью поступающих на входы
автомата-модели входных переменных ![]() и, соответственно этому,
неизменностью снимаемой с выхода выходной
переменной
и, соответственно этому,
неизменностью снимаемой с выхода выходной
переменной ![]() . В то же
время, автоматная модель поведения группы в
динамике, как абстрактная (рис.2), так и
структурная, характеризуется изменением во
времени
. В то же
время, автоматная модель поведения группы в
динамике, как абстрактная (рис.2), так и
структурная, характеризуется изменением во
времени ![]() поступающих на
входы автомата-модели переменных
поступающих на
входы автомата-модели переменных ![]() , принимающих форму входных
процессовx
, принимающих форму входных
процессовx ![]() , и,
соответственно этому, изменением во времени
снимаемой с выхода переменной
, и,
соответственно этому, изменением во времени
снимаемой с выхода переменной ![]() , принимающей форму выходного процесса
, принимающей форму выходного процесса ![]() .
.
4. Методы количественного исследования автоматной модели
Задача определения статического состояния
группы ![]() в произвольный
момент времени
в произвольный
момент времени ![]() по
заданным статическим состояниям всех ее
индивидуумов
по
заданным статическим состояниям всех ее
индивидуумов ![]() в тот же
момент и функции состояния группы (1), в
соответствии с построенной автоматной моделью
статического поведения группы (§ 3, рис.1),
сводится к следующей задаче теории конечных
автоматов - задаче анализа [7]. Задана
комбинационная логическая схема некоторого
статического автомата без памяти (рис.1),
являющаяся моделью статического поведения
группы, реализующая логическую булеву функцию (1),
и ее входные постоянные значения
в тот же
момент и функции состояния группы (1), в
соответствии с построенной автоматной моделью
статического поведения группы (§ 3, рис.1),
сводится к следующей задаче теории конечных
автоматов - задаче анализа [7]. Задана
комбинационная логическая схема некоторого
статического автомата без памяти (рис.1),
являющаяся моделью статического поведения
группы, реализующая логическую булеву функцию (1),
и ее входные постоянные значения ![]() . Требуется определить
соответствующее постоянное выходное значение
схемы
. Требуется определить
соответствующее постоянное выходное значение
схемы ![]() . Последняя
задача может быть решена различными известными
методами анализа, разработанными в теории
конечных автоматов [7]. Заметим, что изложенная в §
3 автоматная модель статического поведения
группы позволяет изучать и более сложные задачи,
связанные со статическим поведением группы, чем
описанная задача определения статического
состояния группы в произвольный момент времени
по заданным статическим состояниям всех ее
индивидуумов и функции состояния группы.
Например, можно рассмотреть и решить задачу
определения множества всех комбинаций
статических состояний индивидуумов
. Последняя
задача может быть решена различными известными
методами анализа, разработанными в теории
конечных автоматов [7]. Заметим, что изложенная в §
3 автоматная модель статического поведения
группы позволяет изучать и более сложные задачи,
связанные со статическим поведением группы, чем
описанная задача определения статического
состояния группы в произвольный момент времени
по заданным статическим состояниям всех ее
индивидуумов и функции состояния группы.
Например, можно рассмотреть и решить задачу
определения множества всех комбинаций
статических состояний индивидуумов ![]() , которым соответствует заданное
статическое состояние группы
, которым соответствует заданное
статическое состояние группы ![]() , если известна функция состояния группы
(1). Эта задача, согласно построенной автоматной
модели статического поведения группы (§ 3, рис.1),
сводится к такой задаче теории конечных
автоматов - задаче статического синтеза входных
воздействий [7]. Задана комбинационная логическая
схема некоторого статического автомата без
памяти (рис.1), являющаяся моделью статического
поведения группы и реализующая логическую
булеву функцию (1), и ее постоянное выходное
значение y. Требуется определить множество всех
входных наборов схемы
, если известна функция состояния группы
(1). Эта задача, согласно построенной автоматной
модели статического поведения группы (§ 3, рис.1),
сводится к такой задаче теории конечных
автоматов - задаче статического синтеза входных
воздействий [7]. Задана комбинационная логическая
схема некоторого статического автомата без
памяти (рис.1), являющаяся моделью статического
поведения группы и реализующая логическую
булеву функцию (1), и ее постоянное выходное
значение y. Требуется определить множество всех
входных наборов схемы ![]() ,
вызывающих на ее выходе данное значение
,
вызывающих на ее выходе данное значение ![]() . Такая задача может быть
решена различными методами синтеза статических
входных воздействий, известными в теории
конечных автоматов [7].
. Такая задача может быть
решена различными методами синтеза статических
входных воздействий, известными в теории
конечных автоматов [7].
Задача нахождения процесса ![]() изменения состояния группы по заданным
процессам
изменения состояния группы по заданным
процессам ![]() , изменения
состояния всех ее индивидуумов и функции
состояния группы (1), в соответствии с
предложенной автоматной моделью динамического
поведения группы (§ 3, рис.2), сводится к следующей
задаче теории динамических автоматов - задаче
динамического анализа [4-6]. Задана комбинационная
логическая схема некоторого динамического
автомата без памяти (рис.2), являющаяся моделью
динамического поведения группы и реализующая
логическую булеву функцию (1), и ее входные
процессы
, изменения
состояния всех ее индивидуумов и функции
состояния группы (1), в соответствии с
предложенной автоматной моделью динамического
поведения группы (§ 3, рис.2), сводится к следующей
задаче теории динамических автоматов - задаче
динамического анализа [4-6]. Задана комбинационная
логическая схема некоторого динамического
автомата без памяти (рис.2), являющаяся моделью
динамического поведения группы и реализующая
логическую булеву функцию (1), и ее входные
процессы ![]() . Требуется
определить соответствующий выходной процесс
схемы
. Требуется
определить соответствующий выходной процесс
схемы ![]() . Последняя
задача может быть решена различными методами
динамического анализа, разработанными в теории
динамических автоматов, в первую очередь,
методом подстановок, позволяющим находить
процессы в узлах схемы последовательно,
продвигаясь от ее входов к выходу.
. Последняя
задача может быть решена различными методами
динамического анализа, разработанными в теории
динамических автоматов, в первую очередь,
методом подстановок, позволяющим находить
процессы в узлах схемы последовательно,
продвигаясь от ее входов к выходу.
Изложенная в § 3 автоматная модель
динамического поведения группы дает возможность
изучать и более сложные проблемы, связанные с
динамическим поведением группы, чем описанная
проблема определения процесса изменения
состояния группы по заданным процессам
изменения состояния всех ее индивидуумов и
функции состояния группы. Так, например, можно
решать задачу определения множества всех или
некоторых комбинаций процессов изменения
состояния индивидуумов ![]() , которым соответствует заданный процесс
изменения состояния группы
, которым соответствует заданный процесс
изменения состояния группы ![]() , если известна функция состояния группы
(1). Эта задача в соответствии с построенной
автоматной моделью динамического поведения
группы (§ 3, рис.2), сводится к такой задаче теории
динамических автоматов - задаче динамического
синтеза входных воздействий [4-6]. Задана
комбинационная логическая схема некоторого
динамического автомата без памяти (рис.2),
являющаяся моделью динамического поведения
группы и реализующая логическую булеву функцию
(1), и ее выходной процесс
, если известна функция состояния группы
(1). Эта задача в соответствии с построенной
автоматной моделью динамического поведения
группы (§ 3, рис.2), сводится к такой задаче теории
динамических автоматов - задаче динамического
синтеза входных воздействий [4-6]. Задана
комбинационная логическая схема некоторого
динамического автомата без памяти (рис.2),
являющаяся моделью динамического поведения
группы и реализующая логическую булеву функцию
(1), и ее выходной процесс ![]() . Требуется найти множество всех или
некоторых наборов процессов на ее входах
. Требуется найти множество всех или
некоторых наборов процессов на ее входах ![]() , вызывающих на ее выходе
процесс
, вызывающих на ее выходе
процесс ![]() . Такая задача
может быть решена различными методами синтеза
динамических входных воздействий, известными в
теории динамических автоматов [4-6]. Далее, можно
решать задачу управления состоянием группы, т.е.
определения моментов и характера управляющих
воздействий, с целью восстановления
работоспособности группы. Эта задача сводится к
1) задаче анализа найденного процесса
. Такая задача
может быть решена различными методами синтеза
динамических входных воздействий, известными в
теории динамических автоматов [4-6]. Далее, можно
решать задачу управления состоянием группы, т.е.
определения моментов и характера управляющих
воздействий, с целью восстановления
работоспособности группы. Эта задача сводится к
1) задаче анализа найденного процесса ![]() изменения состояния
группы, с целью определения по нему моментов
потери группой работоспособности (это моменты
перехода
изменения состояния
группы, с целью определения по нему моментов
потери группой работоспособности (это моменты
перехода ![]() ); 2) задаче
определения управляющего воздействия для
каждого из найденных моментов,
восстанавливающего работоспособность группы.
Управляющие воздействия - это
"восстановление" индивидуумов, включение в
состав группы новых, полезных индивидуумов,
исключения из нее вредных индивидуумов,
изменение алгоритма взаимодействия
индивидуумов и т.д.
); 2) задаче
определения управляющего воздействия для
каждого из найденных моментов,
восстанавливающего работоспособность группы.
Управляющие воздействия - это
"восстановление" индивидуумов, включение в
состав группы новых, полезных индивидуумов,
исключения из нее вредных индивидуумов,
изменение алгоритма взаимодействия
индивидуумов и т.д.
Как следует из изложенного, алгоритмы определения статического поведения группы представляют собой хорошо известные алгоритмы определения статического поведения соответствующего конечного автомата модели группы. В то же время алгоритмы определения динамического поведения группы - это алгоритмы определения поведения динамического автомата-модели группы. Один из этих алгоритмов рассмотрен в следующем параграфе.
5. Алгоритм количественного определения динамики поведения группы
В соответствии с изложенной в § 3 автоматной
моделью динамического поведения группы и
изложенной в § 4 автоматной трактовкой задача
количественного определения динамического
поведения группы алгоритм решения этой задачи
выглядит таким образом. Задано: процессы ![]()
![]() ,
изменения состояния всех индивидуумов и функция
состояния группы (1), заданная предположительно в
неформальном виде. Требуется определить процесс
,
изменения состояния всех индивидуумов и функция
состояния группы (1), заданная предположительно в
неформальном виде. Требуется определить процесс ![]() изменения состояния
группы.
изменения состояния
группы.
Шаг 1. Переход от заданной неформально модели
статического поведения группы в виде
зависимости ее состояния ![]() от состояния индивидуумов x в произвольный
момент времени к соответствующей формальной
модели в виде булевой логической функции
от состояния индивидуумов x в произвольный
момент времени к соответствующей формальной
модели в виде булевой логической функции ![]() состояния группы [формула
(1)]. Переход осуществляется путем выделения в
неформальной статической модели группы тех
комбинаций работоспособных и неработоспособных
состояния индивидуумов, которым соответствуют
работоспособные состояния всей группы. После
этого выражение функции
состояния группы [формула
(1)]. Переход осуществляется путем выделения в
неформальной статической модели группы тех
комбинаций работоспособных и неработоспособных
состояния индивидуумов, которым соответствуют
работоспособные состояния всей группы. После
этого выражение функции ![]() состояния группы записывается в
дизъюнктивной нормальной форме (ДНФ) булевой
алгебры
состояния группы записывается в
дизъюнктивной нормальной форме (ДНФ) булевой
алгебры
![]() (2)
(2)
где ![]() есть
есть ![]() или
или ![]() (булево
логическое отрицание
(булево
логическое отрицание ![]() ),
а
),
а ![]() и
и ![]() - булевы дизъюнкция и конъюнкция. Таким
образом, выражение (2) есть дизъюнкция конъюнкций
двоичных переменных
- булевы дизъюнкция и конъюнкция. Таким
образом, выражение (2) есть дизъюнкция конъюнкций
двоичных переменных ![]() и
их отрицаний
и
их отрицаний ![]() , где
переменная
, где
переменная ![]() соответствует
работоспособному , а ее отрицание
соответствует
работоспособному , а ее отрицание ![]() - неработоспособному состоянию
- неработоспособному состоянию ![]() -го индивидуума. Любая
конъюнкция в (2) описывает одну определенную
комбинацию работоспособных и неработоспособных
состояний индивидуумов, которой соответствует
работоспособное состояние всей группы. При этом
-го индивидуума. Любая
конъюнкция в (2) описывает одну определенную
комбинацию работоспособных и неработоспособных
состояний индивидуумов, которой соответствует
работоспособное состояние всей группы. При этом ![]() (т.е. группа в целом
работоспособна), только если какая-нибудь
конъюнкция в (2) равна 1. Равенство конъюнкции
единице, т.е.
(т.е. группа в целом
работоспособна), только если какая-нибудь
конъюнкция в (2) равна 1. Равенство конъюнкции
единице, т.е. ![]() ,
эквивалентно тому что
,
эквивалентно тому что ![]() ,
что позволяет идентифицировать одну
определенную комбинацию состояний индивидуумов,
которой соответствует работоспособное
состояние группы. Например, равенство
,
что позволяет идентифицировать одну
определенную комбинацию состояний индивидуумов,
которой соответствует работоспособное
состояние группы. Например, равенство ![]() эквивалентно тому, что
эквивалентно тому, что ![]() , что означает следующее:
комбинации "индивидуумы 1,3 работоспособны, а
индивидуум 2 - нет" соответствует
работоспособное состояние всей группы.
, что означает следующее:
комбинации "индивидуумы 1,3 работоспособны, а
индивидуум 2 - нет" соответствует
работоспособное состояние всей группы.
Описанное выделение комбинаций состояний индивидуумов, которым соответствует работоспособное состояние группы, имеет определенную специфику, в зависимости от приятого критерия работоспособности индивидуумов и группы (производительность, надежность, стабильность и т.д.).
Шаг 2. Построение по булевой логической
функции состояния группы ![]() , найденной на шаге 1 и описывающей
некоторый динамический автомат без памяти -
модель изучаемой группы, соответствующей
комбинационной логической схемы, реализующей
эту функцию. Для этого имеющееся выражение (2)
функции
, найденной на шаге 1 и описывающей
некоторый динамический автомат без памяти -
модель изучаемой группы, соответствующей
комбинационной логической схемы, реализующей
эту функцию. Для этого имеющееся выражение (2)
функции ![]() преобразуется
к виду суперпозиции элементарных булевых
логических функций, составляющих некоторый
функционально полный набор. При этом для каждой
элементарной функции принятого набора должны
быть известны (определены заранее) соотношения
между входными и выходными процессами.
Полученное выражение
преобразуется
к виду суперпозиции элементарных булевых
логических функций, составляющих некоторый
функционально полный набор. При этом для каждой
элементарной функции принятого набора должны
быть известны (определены заранее) соотношения
между входными и выходными процессами.
Полученное выражение ![]() упрощается
(минимизируется) в принятом наборе, в
соответствии с законами булевой алгебры [4-7].
Каждой элементарной функции упрощенного
(минимизированного) выражения функции
упрощается
(минимизируется) в принятом наборе, в
соответствии с законами булевой алгебры [4-7].
Каждой элементарной функции упрощенного
(минимизированного) выражения функции ![]() ставится во
взаимно-однозначное соответствие логический
элемент, реализующий эту функцию, а отношению
следования между элементарными функциями (выход
одной функции есть вход другой) - подобное же
отношение между логическими элементами,
реализующими эти функции. В результате выражение
булевой логической функции
ставится во
взаимно-однозначное соответствие логический
элемент, реализующий эту функцию, а отношению
следования между элементарными функциями (выход
одной функции есть вход другой) - подобное же
отношение между логическими элементами,
реализующими эти функции. В результате выражение
булевой логической функции ![]() в виде суперпозиции элементарных функций
переходит в комбинационную логическую схему,
построенную из соответствующих элементарным
булевым логическим функциям логических
элементов и реализующую функцию
в виде суперпозиции элементарных функций
переходит в комбинационную логическую схему,
построенную из соответствующих элементарным
булевым логическим функциям логических
элементов и реализующую функцию ![]() . Построенная комбинационная
логическая схема есть структурная
математическая модель динамического поведения
группы, причем ее входные процессы
. Построенная комбинационная
логическая схема есть структурная
математическая модель динамического поведения
группы, причем ее входные процессы ![]() моделируют динамику изменения во
времени состояния индивидуумов
моделируют динамику изменения во
времени состояния индивидуумов ![]() , а выходной процесс
, а выходной процесс ![]() - динамику изменения во времени
состояния группы.
- динамику изменения во времени
состояния группы.
Шаг 3. Вычисление по входным процессам ![]() построенной на шаге 2
комбинационной логической схемы (модели
динамического поведения группы) ее выходного
процесса
построенной на шаге 2
комбинационной логической схемы (модели
динамического поведения группы) ее выходного
процесса ![]() . Это
вычисление имеет смысл нахождения по известной
динамике изменения состояния всех индивидуумов
. Это
вычисление имеет смысл нахождения по известной
динамике изменения состояния всех индивидуумов ![]() динамики изменения
состояния группы в целом. Такое вычисление
является базовой задачей динамической теории
автоматов и проводится проще всего следующим
методом подстановок: 1) логическая
комбинационная схема-модель разбивается на
последовательные ступени глубиной в один
логический элемент [4-7]; 2) с помощью базовых
операций НЛ
динамики изменения
состояния группы в целом. Такое вычисление
является базовой задачей динамической теории
автоматов и проводится проще всего следующим
методом подстановок: 1) логическая
комбинационная схема-модель разбивается на
последовательные ступени глубиной в один
логический элемент [4-7]; 2) с помощью базовых
операций НЛ ![]() (дизъюнкция
НЛ) и
(дизъюнкция
НЛ) и ![]() (конъюнкция НЛ)
находятся соотношения
(конъюнкция НЛ)
находятся соотношения ![]() между
входными и выходными процессами для всех типов
элементов схемы [4-6]; 3) по заданным входным
процессам схемы
между
входными и выходными процессами для всех типов
элементов схемы [4-6]; 3) по заданным входным
процессам схемы ![]() и
найденным соотношениям
и
найденным соотношениям ![]() определяются
сначала процессы на выходах первой ступени
схемы, по ним - процессы на выходах второй ступени
и т.д. и, наконец, процесс
определяются
сначала процессы на выходах первой ступени
схемы, по ним - процессы на выходах второй ступени
и т.д. и, наконец, процесс ![]() на выходе всей схемы. Найденный процесс
на выходе всей схемы. Найденный процесс ![]() и есть искомый
динамический процесс изменения состояния
группы. Моменты изменения состояния в этой
процессе (т.е. моменты изменения состояния
группы) выражаются через моменты изменения
состояния в процессах
и есть искомый
динамический процесс изменения состояния
группы. Моменты изменения состояния в этой
процессе (т.е. моменты изменения состояния
группы) выражаются через моменты изменения
состояния в процессах ![]() (т.е.
моменты изменения состояния отдельных
индивидуумов) с помощью операций
(т.е.
моменты изменения состояния отдельных
индивидуумов) с помощью операций ![]() и
и ![]() НЛ.
НЛ.
6. Оценки сложности автоматной модели группового поведения и сложности определения динамического поведения группы
Сложность предложенной в § 3 автоматной модели
поведения группы, как в статике, так и в динамике,
определяется числом логических элементов в
комбинационной логической схеме, которая
является структурной моделью указанного
поведения и в качестве таковой реализует булеву
логическую функцию состояния группы (1). Число
входов этой схемы равно числу ![]() индивидуумов в группе, число выходов -1.
Число элементов в схеме, согласно теории
конечных автоматов [7], оценивается в виде
индивидуумов в группе, число выходов -1.
Число элементов в схеме, согласно теории
конечных автоматов [7], оценивается в виде
![]() , (3)
, (3)
где ![]() и
и ![]() - соответственно числа двухвходовых
конъюнкторов (реализуют элементарную
двухместную булеву конъюнкцию), двухвходовых
дизъ-юнкторов (реализуют элементарную
двухместную булеву дизъюнкцию) и инверторов
(реализуют булево отрицание), равные
- соответственно числа двухвходовых
конъюнкторов (реализуют элементарную
двухместную булеву конъюнкцию), двухвходовых
дизъ-юнкторов (реализуют элементарную
двухместную булеву дизъюнкцию) и инверторов
(реализуют булево отрицание), равные
![]() (4)
(4)
Соотношения (3),(4) дают асимптотическую оценку
сложности реализации произвольной булевой
логической функции с ![]() аргументами,
являющейся функцией состояния произвольной
группы из
аргументами,
являющейся функцией состояния произвольной
группы из ![]() индивидуумов.
Эта оценка при
индивидуумов.
Эта оценка при ![]() возрастает
экспоненциально. Однако столь сложно
реализуются не все функции, а лишь наиболее
"плохие" функции, соответствующие "плохо
организованным" группам. "Нормально", а
тем более "хорошо" организованные группы
должны иметь гораздо более просто реализуемые
функции состояния, т.е. более простую структурную
автоматную модель.
возрастает
экспоненциально. Однако столь сложно
реализуются не все функции, а лишь наиболее
"плохие" функции, соответствующие "плохо
организованным" группам. "Нормально", а
тем более "хорошо" организованные группы
должны иметь гораздо более просто реализуемые
функции состояния, т.е. более простую структурную
автоматную модель.
Оценим сложность алгоритма § 5 определения
динамики поведения группы. Пусть число
индивидуумов в группе равно ![]() , а число изменения состояний каждого
индивидуума за изучаемый интервал времени -
, а число изменения состояний каждого
индивидуума за изучаемый интервал времени - ![]() . Считаем, что
комбинационная логическая схема-модель
динамического поведения группы -
. Считаем, что
комбинационная логическая схема-модель
динамического поведения группы - ![]() -ступенчатая, в каждой ступени
которой есть
-ступенчатая, в каждой ступени
которой есть ![]() логических
элементов с
логических
элементов с ![]() входами и
одним выходом каждый, причем входы элемента
любой ступени соединены только с выходами
элементов предыдущей ступени. Ясно, что число
входов данной схемы, равное числу
входами и
одним выходом каждый, причем входы элемента
любой ступени соединены только с выходами
элементов предыдущей ступени. Ясно, что число
входов данной схемы, равное числу ![]() индивидуумов в группе, согласно
конструкции схемы равно
индивидуумов в группе, согласно
конструкции схемы равно ![]() , так что
, так что
![]() . (5)
. (5)
Это же число входов имеется у каждой ступени
схемы. Число изменений процесса, действующего на
любом ![]() -м входе нашей
схемы, в соответствии с принятой моделью
поведения группы (§ 3) равно числу
-м входе нашей
схемы, в соответствии с принятой моделью
поведения группы (§ 3) равно числу ![]() изменения состояний
соответствующего
изменения состояний
соответствующего ![]() -го
индивидуума.
-го
индивидуума.
Как показано в [8], сложность вычисления
динамического процесса на выходе приведенной
комбинационной логической схемы-модели, которая
и есть сложность определения динамики поведения
группы в соответствии с алгоритмом § 5,
оценивается следующим выражением (в котором еще ![]() надо согласно (5) заменить
на
надо согласно (5) заменить
на ![]() )
)
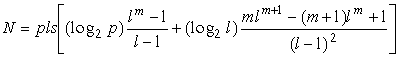 (6)
(6)
При большом числе ![]() ступеней
схемы-модели оценка (6) упрощается и с учетом того,
что
ступеней
схемы-модели оценка (6) упрощается и с учетом того,
что ![]() , принимает вид
, принимает вид
![]() (7)
(7)
Как следует из (7), сложность определения
динамики поведения группы с помощью
предложенной автоматной модели и
соответствующего ей алгоритма находится в
положительной степенной зависимости от числа ![]() индивидуумов в группе и
числа
индивидуумов в группе и
числа ![]() изменения их
состояний за изучаемое время, отрицательной
степенной зависимости от числа
изменения их
состояний за изучаемое время, отрицательной
степенной зависимости от числа ![]() элементов в одной ступени
схемы-модели и в экспоненциальной зависимости от
длины схемы
элементов в одной ступени
схемы-модели и в экспоненциальной зависимости от
длины схемы ![]() . Таким
образом, для снижения указанной сложности
следует стремиться к построению комбинационных
логических схем-моделей поведения групп с
минимальной длиной
. Таким
образом, для снижения указанной сложности
следует стремиться к построению комбинационных
логических схем-моделей поведения групп с
минимальной длиной ![]() и
максимальным числом
и
максимальным числом ![]() элементов
в одной ступени.
элементов
в одной ступени.
7. Пример определения динамики поведения группы
Рассмотрим группу из трех индивидуумов: 1, 2 и 3,
обладающих производительностью соответственно
3, 4 и 2 единицы. Группа работоспособна, если ее
суммарная производительность составляет не
менее 6 единиц. Индивидуумы 1,2,3 работоспособны
(обеспечивают указанную производительность)
соответственно на интервалах времени ![]() . Требуется определить
динамику изменения состояния группы во времени,
т.е. интервалы ее работоспособности и
неработоспособности.
. Требуется определить
динамику изменения состояния группы во времени,
т.е. интервалы ее работоспособности и
неработоспособности.
Применим алгоритм п.5.
Шаг 1. Переход от заданной неформально модели
статического поведения группы к соответствующей
формальной модели - булевой логической функции ![]() состояния группы. Из
условия задачи следует, что имеется только три
комбинации состояний индивидуумов, которым
соответствует работоспособное состояние группы:
1) индивидуумы 1 и 2 работоспособны, индивидуум 3
неработоспособен; 2) индивидуумы 2 и 3
работоспособны, индивидуум 1 неработоспособен; 3)
индивидуумы 1, 2 и 3 работоспособны. Выделенным
комбинациям состояний индивидуумов
соответствует следующее выражение функции
состояния группы. Из
условия задачи следует, что имеется только три
комбинации состояний индивидуумов, которым
соответствует работоспособное состояние группы:
1) индивидуумы 1 и 2 работоспособны, индивидуум 3
неработоспособен; 2) индивидуумы 2 и 3
работоспособны, индивидуум 1 неработоспособен; 3)
индивидуумы 1, 2 и 3 работоспособны. Выделенным
комбинациям состояний индивидуумов
соответствует следующее выражение функции ![]() состояний группы в ДНФ
булевой алгебры логики (в данном случае - это
дизъюнкция трех конъюнкций)
состояний группы в ДНФ
булевой алгебры логики (в данном случае - это
дизъюнкция трех конъюнкций)
![]() (8)
(8)
Здесь ![]() означает,
работоспособное (неработоспособное) состояние
означает,
работоспособное (неработоспособное) состояние ![]() -го индивидуума, а
-го индивидуума, а ![]() - аналогичное состояние
всей группы.
- аналогичное состояние
всей группы.
Шаг 2. Построение по функции состояния (8),
найденной на шаге 1, соответствующей
комбинационной логической схемы, реализующей
эту функцию. Так как функция (8) представлена в
виде ДНФ – дизъюнкции трех трехместных
конъюнкций, а элементарными являются лишь
двухместные функции, реализуемые двухвходовыми
логическими элементами, то необходимо
преобразовать выражение (8), представив его в виде
суперпозиции элементарных функций и затем
минимизировав. Добавив в правую часть (8) еще одну
третью скобку (что согласно закону
идемпотентности булевой алгебры логики ![]() не меняет величины
выражения), объединив одну такую скобку с первой,
а другую - со второй скобками и вынеся из каждой
пары за скобки общие буквы, получим после
упрощений, с учетом законов
не меняет величины
выражения), объединив одну такую скобку с первой,
а другую - со второй скобками и вынеся из каждой
пары за скобки общие буквы, получим после
упрощений, с учетом законов ![]() , нужное представление
, нужное представление
![]() . (9)
. (9)
Поставив в соответствие двухместным дизъюнкции и конъюнкциям в (9) соответствующие логические элементы, получим комбинационную логическую схему-модель динамического поведения группы (рис.3).
Шаг 3. Вычисляем выходной процесс ![]() схемы-модели
динамического поведения группы (рис.3),
моделирующей изменение во времени состояния
группы. Входные процессы этой схемы,
моделирующие изменение во времени состояний
индивидуумов, имеют, согласно условиям задачи,
вид единичных импульсов в соответствующих
интервалах времени
схемы-модели
динамического поведения группы (рис.3),
моделирующей изменение во времени состояния
группы. Входные процессы этой схемы,
моделирующие изменение во времени состояний
индивидуумов, имеют, согласно условиям задачи,
вид единичных импульсов в соответствующих
интервалах времени
![]() (10)
(10)
По формулам динамической теории автоматов [4-6] находим сначала процессы на выходах первой ступени схемы рис.3
![]()
затем - искомый процесс на выходе второй ступени схемы, задающий процесс изменения во времени состояния группы
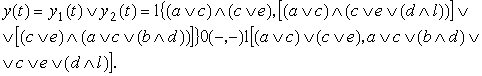
Здесь ![]() - импульсы в
соответствующих интервалах времени,
- импульсы в
соответствующих интервалах времени, ![]() - промежуточная пауза, а
- промежуточная пауза, а ![]() и
и ![]() - операции дизъюнкции и конъюнкции НЛ.
После раскрытия скобок согласно
распределительному закону НЛ
- операции дизъюнкции и конъюнкции НЛ.
После раскрытия скобок согласно
распределительному закону НЛ
![]()
и упрощения по законам поглощения ![]() и тавтологии
и тавтологии ![]() получим окончательно
получим окончательно
![]() (11)
(11)
Согласно выражению (11) в общем случае имеется
два интервала времени, где состояние группы ![]() , т.е. группа
работоспособна. Они указаны в квадратных скобках
выражения. В остальных временных интервалах
группа неработоспособна.
, т.е. группа
работоспособна. Они указаны в квадратных скобках
выражения. В остальных временных интервалах
группа неработоспособна.
Основываясь на полученном выражении (11) процесса динамического поведения группы, можно решить и ряд других задач, связанных с этим поведением, например, задачу управления состоянием группы.
8. Заключение
Предложенная новая математическая модель динамического поведения социальных групп - динамический конечный автомат, в сочетании с адекватным математическим аппаратом изучения динамических автоматов - непрерывной логикой, позволяет, как показано в статье, выполнять в символической форме расчет и анализ процесса изменения состояния группы во времени. Это, в свою очередь, открывает путь к решению новых, более сложных задач изучения динамического поведения групп. Было бы целесообразно распространить предложенный подход на случай групп с большим числом индивидуумов. В этом случае сама математическая автоматная модель динамического поведения группы остается в силе, однако появляется проблема "проклятия размерности", для разрешения которой необходимо привлечь адекватный математический аппарат порядковых определителей [5,6], представляющий собой многомерное обобщение аппарата непрерывной логики. Кроме того, представляется важным распространение предложенного подхода на случай возможности неопределенных состояний индивидуумов и группы, промежуточных между состояниями работоспособности и неработоспособности. В этом случае описанная математическая автоматная модель динамического поведения группы должна быть усовершенствована, путем включения в нее неопределенных состояний и сигналов. Соответствующий класс динамических автоматов известен [6].
Литература
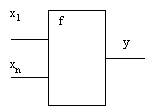
Рис. 1 Математическая автоматная модель
статического поведения группы (![]() - переменная состояния
- переменная состояния ![]() -го индивидуума,
-го индивидуума, ![]() - переменная состояния группы,
- переменная состояния группы, ![]() - логическая булева
функция состояния группы).
- логическая булева
функция состояния группы).
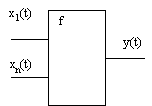
Рис. 2. Математическая автоматная модель
динамического поведения группы (![]() - процесс изменения состояния
- процесс изменения состояния ![]() -го индивидуума,
-го индивидуума, ![]() - процесс изменения
состояния группы,
- процесс изменения
состояния группы, ![]() -логическая
булева функция состояния группы).
-логическая
булева функция состояния группы).
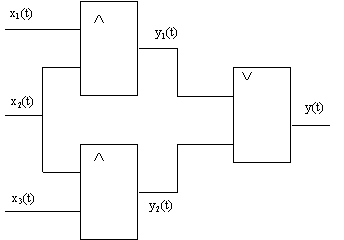
Рис. 3. Структурная автоматная модель динамического поведения неко-торой группы с тремя индивидуумами.
DYNAMIC AUTOMATON AND MODELING SPEAKERS OF SOCIAL GROUPS
V. I. Levin
Here is given new model of dynamical behaviour of social
group-dynamical finite automata. In the article the dynamics of ![]() -th individual's behaviour models by process on
-th individual's behaviour models by process on ![]() -th input of automata, dynamics of all group's
conduct by process on its output, and statical dependence of all group's state from
individuals' state by Boolean logical function for automata. For quantitative studing of
model are supposed methods of modern theory of dinamical automatas based on mathematical
apparatus of continuous logic, that give us possibility to get results in symbolical form.
-th input of automata, dynamics of all group's
conduct by process on its output, and statical dependence of all group's state from
individuals' state by Boolean logical function for automata. For quantitative studing of
model are supposed methods of modern theory of dinamical automatas based on mathematical
apparatus of continuous logic, that give us possibility to get results in symbolical form.
Поступила в редакцию 27.07.2001.