УДК 519.1
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ОБРАЗОВАНИЯ КОЛЛЕКТИВА ИЗ ИНДИВИДУУМОВ
© 2001 г. В. И. Левин
Показана эквивалентность задачи определения условий возникновения и исчезновения коллектива и задачи нахождения отклика динамического автомата на заданные входные процессы. На этой основе предложено автоматное моделирование коллектива. Использованы непрерывная логика и логические определители.
Введение
Хорошо известно, что люди в состоянии
успешно заниматься социально-экономической
деятельностью только тогда, когда они образуют
некоторый коллектив. На практике образование
коллектива возможно далеко не всегда. Дело в том,
что люди значительную часть своего времени ![]() тратят на личные дела, и
тогда они не могут быть участниками какого-либо
коллектива. Остальную часть времени люди могут
использовать, войдя в тот или иной коллектив.
Ясно, что при
тратят на личные дела, и
тогда они не могут быть участниками какого-либо
коллектива. Остальную часть времени люди могут
использовать, войдя в тот или иной коллектив.
Ясно, что при ![]() образование
коллектива невозможно – люди в этом крайнем
случае образуют просто толпу. В другом крайнем
случае, при
образование
коллектива невозможно – люди в этом крайнем
случае образуют просто толпу. В другом крайнем
случае, при ![]() , создаются
наилучшие условия для создания коллектива.
Реально
, создаются
наилучшие условия для создания коллектива.
Реально ![]() , причем
сложность состоит в том, что интервалы времени, в
которых человек занят личными делами, чередуются
с интервалами, когда он свободен и потому может
быть участником коллектива. Таким образом,
важная задача изучения процесса
последовательного превращения толпы в коллектив
и обратно оказывается сложной динамической
задачей. Для ее решения применяют различные
подходы: кибернетическое моделирование [1],
методы математической социологии [2] и прикладной
социологии [3], методы социальной психологии [4]. В
работе [5] автором была предложена
автоматно-логическая методика изучения
коллектива, позволившая решить ряд задач
математического моделирования и управления
коллективом [6,7]. В настоящей статье показано, что
эта методика удобна также для моделирования
процессов образования и распада коллектива.
, причем
сложность состоит в том, что интервалы времени, в
которых человек занят личными делами, чередуются
с интервалами, когда он свободен и потому может
быть участником коллектива. Таким образом,
важная задача изучения процесса
последовательного превращения толпы в коллектив
и обратно оказывается сложной динамической
задачей. Для ее решения применяют различные
подходы: кибернетическое моделирование [1],
методы математической социологии [2] и прикладной
социологии [3], методы социальной психологии [4]. В
работе [5] автором была предложена
автоматно-логическая методика изучения
коллектива, позволившая решить ряд задач
математического моделирования и управления
коллективом [6,7]. В настоящей статье показано, что
эта методика удобна также для моделирования
процессов образования и распада коллектива.
Пусть имеется совокупность ![]() индивидуумов. Каждый
индивидуум может находиться в одном из двух
состояний: 1) состояние индивидуализма, т.е.
способности заниматься только своими личными
делами; 2) состояние коллективизма, т.е.
способности заниматься общими для всех
индивидуумов делами. По определению, заданная
совокупность индивидуумов образует в
произвольный момент времени
индивидуумов. Каждый
индивидуум может находиться в одном из двух
состояний: 1) состояние индивидуализма, т.е.
способности заниматься только своими личными
делами; 2) состояние коллективизма, т.е.
способности заниматься общими для всех
индивидуумов делами. По определению, заданная
совокупность индивидуумов образует в
произвольный момент времени ![]() коллектив, если, по крайней мере,
коллектив, если, по крайней мере, ![]() из них (безразлично, кто
именно) находятся в этот момент в состоянии
коллективизма; в противном случае эта
совокупность образует толпу. Ясно, что пороговое
значение
из них (безразлично, кто
именно) находятся в этот момент в состоянии
коллективизма; в противном случае эта
совокупность образует толпу. Ясно, что пороговое
значение ![]() должно быть
достаточно большим (близким к
должно быть
достаточно большим (близким к ![]() ); однако конкретное значение
); однако конкретное значение ![]() должно оговариваться отдельно для
каждой ситуации. Задана динамика изменения
состояний всех индивидуумов, в виде
последовательности моментов времени, в которых
происходит изменение состояния индивидуума или,
что эквивалентно, последовательности интервалов
времени с одним и тем же состоянием индивидуума.
Требуется определить динамику изменения
состояний совокупности индивидуумов в целом, т.е.
последовательность моментов времени, в которых
происходит изменение состояния этой
совокупности (превращение из коллектива в толпу
и обратно) или, что эквивалентно,
последовательность интервалов времени с одним и
тем же ее состоянием (коллектив или толпа).
должно оговариваться отдельно для
каждой ситуации. Задана динамика изменения
состояний всех индивидуумов, в виде
последовательности моментов времени, в которых
происходит изменение состояния индивидуума или,
что эквивалентно, последовательности интервалов
времени с одним и тем же состоянием индивидуума.
Требуется определить динамику изменения
состояний совокупности индивидуумов в целом, т.е.
последовательность моментов времени, в которых
происходит изменение состояния этой
совокупности (превращение из коллектива в толпу
и обратно) или, что эквивалентно,
последовательность интервалов времени с одним и
тем же ее состоянием (коллектив или толпа).
Поставим в соответствие состоянию
коллективизма любого индивидуума двоичное
значение 1, а его состоянию индивидуализма –
двоичное значение 0. Тогда переменному двоичному
состоянию произвольного ![]() -го
индивидуума будет соответствовать двоичная
переменная
-го
индивидуума будет соответствовать двоичная
переменная ![]() . Далее,
поставим в соответствие состоянию совокупности
индивидуумов, образующих коллектив, двоичное
значение 1, а состоянию совокупности
индивидуумов, образующих толпу, двоичное
значение 0. Тогда переменному двоичному
состоянию совокупности индивидуумов будет
соответствовать двоичная переменная
. Далее,
поставим в соответствие состоянию совокупности
индивидуумов, образующих коллектив, двоичное
значение 1, а состоянию совокупности
индивидуумов, образующих толпу, двоичное
значение 0. Тогда переменному двоичному
состоянию совокупности индивидуумов будет
соответствовать двоичная переменная ![]() . По условию задачи,
состояние любого индивидуума зависит от времени.
При этом заданная динамика изменения состояния
любого
. По условию задачи,
состояние любого индивидуума зависит от времени.
При этом заданная динамика изменения состояния
любого ![]() -го индивидуума
может быть представлена в виде двоичного
процесса
-го индивидуума
может быть представлена в виде двоичного
процесса ![]() . Из условия
задачи также следует, что состояние совокупности
индивидуумов тоже зависит от времени. При этом
искомая динамика изменения состояния
совокупности индивидуумов может быть
представлена в виде двоичного процесса
. Из условия
задачи также следует, что состояние совокупности
индивидуумов тоже зависит от времени. При этом
искомая динамика изменения состояния
совокупности индивидуумов может быть
представлена в виде двоичного процесса ![]() . Таким образом,
поставленная задача может быть сформулирована
как задача нахождения неизвестного двоичного
процесса
. Таким образом,
поставленная задача может быть сформулирована
как задача нахождения неизвестного двоичного
процесса ![]() по заданным
двоичным процессам
по заданным
двоичным процессам ![]() .
Для ее решения в этой новой форме учтем
следующее. По условию задачи, двоичное состояние
.
Для ее решения в этой новой форме учтем
следующее. По условию задачи, двоичное состояние ![]() совокупности
индивидуумов в произвольный момент времени
совокупности
индивидуумов в произвольный момент времени ![]() однозначно определяется
множеством состояний всех индивидуумов
однозначно определяется
множеством состояний всех индивидуумов ![]() в этот же момент времени.
Это означает, что зависимость
в этот же момент времени.
Это означает, что зависимость ![]() от
от ![]() можно
представить в виде некоторой булевой логической
функции состояния совокупности индивидуумов
можно
представить в виде некоторой булевой логической
функции состояния совокупности индивидуумов
![]() .
(2.1)
.
(2.1)
Булева логическая функция (2.1) задает
некоторый динамический автомат без памяти с
двоичными входами ![]() и
двоичным выходом
и
двоичным выходом ![]() . Эта
функция (этот автомат) реализуется
соответствующей комбинационной логической
схемой, построенной из подходящих логических
элементов [5-7]. Таким образом, динамический
автомат без памяти, реализующий булеву
логическую функцию (2.1), является абстрактной
математической моделью динамического поведения
заданной совокупности индивидуумов, а
соответствующая комбинационная логическая
схема, реализующая указанную функцию, является
структурной математической моделью этого
поведения.
. Эта
функция (этот автомат) реализуется
соответствующей комбинационной логической
схемой, построенной из подходящих логических
элементов [5-7]. Таким образом, динамический
автомат без памяти, реализующий булеву
логическую функцию (2.1), является абстрактной
математической моделью динамического поведения
заданной совокупности индивидуумов, а
соответствующая комбинационная логическая
схема, реализующая указанную функцию, является
структурной математической моделью этого
поведения.
Теперь поставленная задача может быть
удобно сформулирована в терминах автоматной
модели заданной системы. Именно, имеется
динамический автомат без памяти с ![]() двоичными входами
двоичными входами ![]() и 1 двоичным выходом
и 1 двоичным выходом ![]() , на котором реализуется некоторая
неизвестная булева логическая функция входов
(2.1), определяемая условиями задачи. Заданы
входные процессы автомата
, на котором реализуется некоторая
неизвестная булева логическая функция входов
(2.1), определяемая условиями задачи. Заданы
входные процессы автомата ![]() . Требуется найти выходной процесс
автомата
. Требуется найти выходной процесс
автомата ![]() .
.
Сформулированная задача может быть
решена методами динамической теории автоматов
[5,8], а именно: 1) по условиям задачи составляется
булева логическая функция состояния
совокупности индивидуумов (2.1); 2) по составленной
функции строится комбинационная логическая
схема некоторого динамического автомата без
памяти, реализующая эту функцию; построенная
схема является структурной математической
моделью динамического поведения заданной
совокупности индивидуумов; 3) полученная схема
разбивается на последовательные ступени
глубиной в один элемент; 4) по методике [5,8]
находятся соотношения ![]() между
входными и выходными процессами для всех типов
элементов схемы; как показано в [8], эти
соотношения полностью описываются с помощью
базовых операций непрерывной логики (НЛ)
между
входными и выходными процессами для всех типов
элементов схемы; как показано в [8], эти
соотношения полностью описываются с помощью
базовых операций непрерывной логики (НЛ) ![]() (дизъюнкция) и
(дизъюнкция) и ![]() (конъюнкция); 5) по заданным
входным процессам схемы
(конъюнкция); 5) по заданным
входным процессам схемы ![]() и найденным соотношениям
и найденным соотношениям ![]() определяются сначала процессы на
выходах ее 1-й ступени, затем по ним – процессы на
выходах 2-й ступени и т.д. и, наконец, процесс
определяются сначала процессы на
выходах ее 1-й ступени, затем по ним – процессы на
выходах 2-й ступени и т.д. и, наконец, процесс ![]() на выходе всей схемы.
Процесс
на выходе всей схемы.
Процесс ![]() и есть искомый
динамический процесс изменения состояния
совокупности индивидуумов. При этом интервалы
времени со значениями процесса
и есть искомый
динамический процесс изменения состояния
совокупности индивидуумов. При этом интервалы
времени со значениями процесса ![]() представляет те временные
интервалы, в которых заданная совокупность
индивидуумов образует коллектив, а интервалы со
значениями процесса
представляет те временные
интервалы, в которых заданная совокупность
индивидуумов образует коллектив, а интервалы со
значениями процесса ![]() -
временные интервалы, где указанная совокупность
представляет собой толпу. Как видно из
приведенного алгоритма, моменты изменения
состояния совокупности индивидуумов (моменты
изменения в процессе
-
временные интервалы, где указанная совокупность
представляет собой толпу. Как видно из
приведенного алгоритма, моменты изменения
состояния совокупности индивидуумов (моменты
изменения в процессе ![]() )
выражаются через моменты изменения состояния
отдельных индивидуумов (моменты изменения в
процессах
)
выражаются через моменты изменения состояния
отдельных индивидуумов (моменты изменения в
процессах ![]() ) с помощью
операций НЛ
) с помощью
операций НЛ ![]() (дизъюнкция)
и
(дизъюнкция)
и ![]() (конъюнкция).
(конъюнкция).
Приступим к решению задачи, используя приведенный в §1 алгоритм.
Шаг 1. По условиям задачи,
совокупность индивидуумов образует в
произвольный момент времени ![]() коллектив, если в этот момент, по крайней
мере
коллектив, если в этот момент, по крайней
мере ![]() индивидуумов
(безразлично, кто именно) находятся в состоянии
коллективизма. Введем в рассмотрение булеву
логическую функцию
индивидуумов
(безразлично, кто именно) находятся в состоянии
коллективизма. Введем в рассмотрение булеву
логическую функцию ![]() от
переменных состояния индивидуумов
от
переменных состояния индивидуумов ![]() , равную по определению 1, если ровно
, равную по определению 1, если ровно ![]() из этих переменных
(безразлично, какие именно) равны 1. Тогда
переменная состояния совокупности индивидуумов
из этих переменных
(безразлично, какие именно) равны 1. Тогда
переменная состояния совокупности индивидуумов ![]() может быть выражена в виде
может быть выражена в виде
![]() , (3.1)
, (3.1)
где ![]() есть
операция булевой дизъюнкции. Но, как следует из
булевой алгебры логики [8], функция
есть
операция булевой дизъюнкции. Но, как следует из
булевой алгебры логики [8], функция ![]() есть не что иное, как симметрическая
булева логическая функция от переменных
есть не что иное, как симметрическая
булева логическая функция от переменных ![]() индекса
индекса ![]() , ее стандартное обозначение
, ее стандартное обозначение ![]() . Свойства таких функций
для произвольных значений индекса
. Свойства таких функций
для произвольных значений индекса ![]() детально изучены [8]. Подставляя в (3.1)
выражение функций
детально изучены [8]. Подставляя в (3.1)
выражение функций ![]() в
виде симметрических функций
в
виде симметрических функций ![]() , получим явное представление булевой
логической функции состояния совокупности
индивидуумов
, получим явное представление булевой
логической функции состояния совокупности
индивидуумов
![]() , (3.2)
, (3.2)
выраженное только через известные
функции ![]() с помощью
операций булевой дизъюнкции
с помощью
операций булевой дизъюнкции ![]() .
.
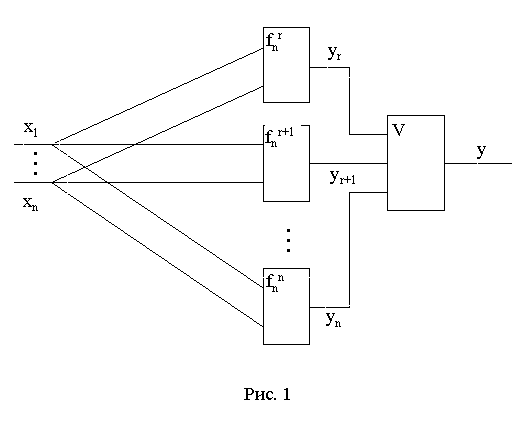
Шаг 2. По составленной функции
состояния системы (3.2) строим соответствующую
комбинационную логическую схему динамического
автомата без памяти (рис. 1). Эта схема есть
структурная математическая модель изучаемой
совокупности индивидуумов. Она состоит из ![]() подсхем (элементов),
реализующих соответствующие симметрические
логические функции
подсхем (элементов),
реализующих соответствующие симметрические
логические функции ![]() , и
имеющих каждая по
, и
имеющих каждая по ![]() входов
входов
![]() , и одного
, и одного ![]() -входового элемента ИЛИ,
реализующего на выходе
-входового элемента ИЛИ,
реализующего на выходе ![]() булеву
логическую дизъюнкцию
булеву
логическую дизъюнкцию ![]() своих
входов
своих
входов ![]() , являющихся
выходами указанных подсхем.
, являющихся
выходами указанных подсхем.
Шаг 3. Разбиваем схему рис. 1 на две
последовательные ступени глубиной в один
элемент. 1-я ступень состоит из ![]() работающих параллельно элементов,
реализующих симметрические логические функции
работающих параллельно элементов,
реализующих симметрические логические функции ![]() , от
, от ![]() входных переменных
входных переменных ![]() и имеющих выходы
и имеющих выходы ![]() .
2-я ступень содержит единственный элемент со
входами
.
2-я ступень содержит единственный элемент со
входами ![]() и выходом
и выходом ![]() , на котором реализуется
булева логическая функция – дизъюнкция входов.
, на котором реализуется
булева логическая функция – дизъюнкция входов.
Шаг 4. Соотношение между входными ![]() и выходными
и выходными ![]() процессами произвольного
процессами произвольного ![]() -го,
-го, ![]() элемента 1-й ступени схемы рис. 1 дается
следующей формулой динамической теории
автоматов [8]. Пусть двоичные входные процессы
схемы рис. 1
элемента 1-й ступени схемы рис. 1 дается
следующей формулой динамической теории
автоматов [8]. Пусть двоичные входные процессы
схемы рис. 1 ![]() , являющиеся
также входными процессами произвольного
, являющиеся
также входными процессами произвольного ![]() -го,
-го, ![]() , элемента 1-й ступени схемы и моделирующие
динамику изменения состояния произвольного
, элемента 1-й ступени схемы и моделирующие
динамику изменения состояния произвольного ![]() -го
-го ![]() индивидуума, имеют вид произвольных
последовательностей импульсов
индивидуума, имеют вид произвольных
последовательностей импульсов ![]() и пауз
и пауз ![]() в
соответствующих временных интервалах
в
соответствующих временных интервалах ![]() и
и ![]() .
.
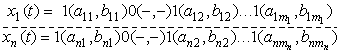 (3.3)
(3.3)
Тогда двоичный процесс ![]() на выходе
на выходе ![]() -го,
-го,
![]() , элемента ступени
имеет вид
, элемента ступени
имеет вид
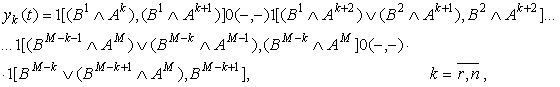 (3.4)
(3.4)
где ![]() и
и ![]() - так называемые
логические определители (ЛО) ранга
- так называемые
логические определители (ЛО) ранга ![]() , составленные соответственно из
моментов
, составленные соответственно из
моментов ![]() изменений
изменений ![]() во входных процессах (3.3) и
из моментов
во входных процессах (3.3) и
из моментов ![]() изменений
изменений ![]() в этих процессах [8]
в этих процессах [8]
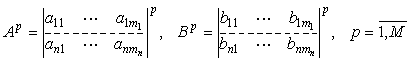 ; (3.5)
; (3.5)
M – общее число элементов в каждом ЛО [общее число изменений каждого вида во входных процессах (3.3)], означающее общее число интервалов коллективизма всех индивидуумов, определяемое по формуле
![]() ; (3.6)
; (3.6)
![]()
![]() - операция
конъюнкции НЛ,
- операция
конъюнкции НЛ, ![]() -
операция дизъюнкции НЛ. По определению, ЛО
-
операция дизъюнкции НЛ. По определению, ЛО ![]() вида (3.5) есть функция –
отображение множества элементов определителя в
его
вида (3.5) есть функция –
отображение множества элементов определителя в
его ![]() -й в порядке
возрастания элемент. ЛО
-й в порядке
возрастания элемент. ЛО ![]() (и
аналогично
(и
аналогично ![]() ) выражается
через свои элементы по формуле
) выражается
через свои элементы по формуле
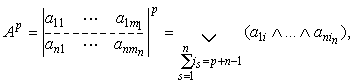 (3.7)
(3.7)
в частности, ![]()
где ![]() и
и ![]() - дизъюнкция и конъюнкция
НЛ; элемент
- дизъюнкция и конъюнкция
НЛ; элемент ![]() в (3.7)
опускается, если из записанного условия для
суммы
в (3.7)
опускается, если из записанного условия для
суммы ![]() получается
получается ![]() .
.
Соотношение между входными ![]() и выходным
и выходным ![]() процессами единственного элемента
2-й ступени схемы рис. 1 – дизъюнктора дается
следующей формулой [8]. Пусть двоичные процессы
процессами единственного элемента
2-й ступени схемы рис. 1 – дизъюнктора дается
следующей формулой [8]. Пусть двоичные процессы ![]() на входах дизъюнктора
имеют общий вид, аналогичный (3.3):
на входах дизъюнктора
имеют общий вид, аналогичный (3.3):
![]() . (3.8)
. (3.8)
Тогда двоичный процесс ![]() на его выходе, моделирующий динамику
изменения состояния совокупности индивидуумов,
имеет вид
на его выходе, моделирующий динамику
изменения состояния совокупности индивидуумов,
имеет вид
![]() , (3.9)
, (3.9)
где ![]() и
и ![]() - ЛО ранга
- ЛО ранга ![]() , составленные соответственно из
моментов
, составленные соответственно из
моментов ![]() изменений
изменений ![]() во входных процессах (3.8) и
из моментов
во входных процессах (3.8) и
из моментов ![]() изменений
изменений ![]() в этих процессах и
аналогичные ЛО
в этих процессах и
аналогичные ЛО ![]() , т.е.
, т.е.
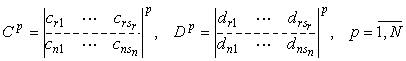 ; (3.10)
; (3.10)
![]() -
общее число элементов в каждом ЛО [общее число
изменений каждого вида во входных процессах (3.8)]
равное
-
общее число элементов в каждом ЛО [общее число
изменений каждого вида во входных процессах (3.8)]
равное
![]() ; (3.11)
; (3.11)
![]() -
операция конъюнкции НЛ. ЛО
-
операция конъюнкции НЛ. ЛО ![]() и
и ![]() выражаются
через свои элементы по формуле (8).
выражаются
через свои элементы по формуле (8).
Шаг 5. Процессы ![]() , на выходах 1-й ступени схемы рис. 1 уже
определены выше (см. формулу (3.4)). Процесс
, на выходах 1-й ступени схемы рис. 1 уже
определены выше (см. формулу (3.4)). Процесс ![]() на выходе 2-й ступени этой
схемы есть процесс на выходе
элемента-дизъюнктора, образующего эту ступень и
получающего по своим входам
на выходе 2-й ступени этой
схемы есть процесс на выходе
элемента-дизъюнктора, образующего эту ступень и
получающего по своим входам ![]() выходные процессы
выходные процессы ![]() предшествующей ступени. Таким образом,
процесс
предшествующей ступени. Таким образом,
процесс ![]() можно
определить по общей формуле (3.9), учитывая, что в
нашем случае дизъюнктор имеет входные процессы
вида (3.8), в которых моменты изменений и их число
выражаются конкретно согласно формуле (3.4). В
результате получим для процесса
можно
определить по общей формуле (3.9), учитывая, что в
нашем случае дизъюнктор имеет входные процессы
вида (3.8), в которых моменты изменений и их число
выражаются конкретно согласно формуле (3.4). В
результате получим для процесса ![]() общее выражение (3.9), в котором ЛО
общее выражение (3.9), в котором ЛО ![]() и
и ![]() и число
и число ![]() конкретизированы
следующим образом
конкретизированы
следующим образом
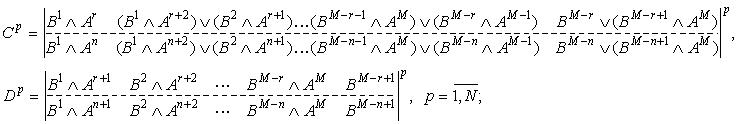 (3.12)
(3.12)
![]() , (3.13)
, (3.13)
где ![]() определяется
по формуле (3.6).
определяется
по формуле (3.6).
Согласно §1, полученный процесс ![]() , определяемый формулами
(3.9), (3.12), (3.13), (3.6), и есть динамический процесс
изменения состояния заданной совокупности
индивидуумов. Причем в интервалах времени, где
значение процесса
, определяемый формулами
(3.9), (3.12), (3.13), (3.6), и есть динамический процесс
изменения состояния заданной совокупности
индивидуумов. Причем в интервалах времени, где
значение процесса ![]() , эта
совокупность образует коллектив, а в остальных
интервалах времени, где значение процесса
, эта
совокупность образует коллектив, а в остальных
интервалах времени, где значение процесса ![]() - толпу. Из формул (3.9), (3.12),
(3.13), (3.6) видно, что моменты изменения состояния
совокупности индивидуумов выражаются через
моменты изменения состояния отдельных
индивидуумов (моменты изменения в процессах
- толпу. Из формул (3.9), (3.12),
(3.13), (3.6) видно, что моменты изменения состояния
совокупности индивидуумов выражаются через
моменты изменения состояния отдельных
индивидуумов (моменты изменения в процессах ![]() ) с помощью операций НЛ
дизъюнкции
) с помощью операций НЛ
дизъюнкции ![]() и
конъюнкции
и
конъюнкции ![]() . Полученный
результат показывает, что изученная
совокупность индивидуумов в общем случае имеет
. Полученный
результат показывает, что изученная
совокупность индивидуумов в общем случае имеет ![]() интервалов времени
(формула (3.13)), на которых она образует коллектив.
В конкретных случаях, при конкретных числовых
параметров процессов
интервалов времени
(формула (3.13)), на которых она образует коллектив.
В конкретных случаях, при конкретных числовых
параметров процессов ![]() изменения
состояния отдельных индивидуумов
изменения
состояния отдельных индивидуумов ![]() , количество интервалов может быть
меньше
, количество интервалов может быть
меньше ![]() , из-за
вырождения некоторых из них. Выведенные формулы
(3.9), (3.12), (3.13), (3.6) позволяют эффективно вычислять
процесс
, из-за
вырождения некоторых из них. Выведенные формулы
(3.9), (3.12), (3.13), (3.6) позволяют эффективно вычислять
процесс ![]() изменения
состояния совокупности индивидуумов при любых
конкретно заданных процессах
изменения
состояния совокупности индивидуумов при любых
конкретно заданных процессах ![]() изменения состояния самих индивидуумов.
изменения состояния самих индивидуумов.
Полученное в § 3 решение задачи моделирования поведения совокупности индивидуумов представлено в аналитической форме [см. формулы (3.9), (3.12), (3.13), (3.6)]. Это позволяет проанализировать данное решение. При этом интерес представляют, в первую очередь, следующие вопросы: 1) На каких интервалах времени совокупность индивидуумов всегда образует толпу, а на каких всегда образует коллектив? 2) На каких интервалах времени совокупность индивидуумов, в зависимости от условий, может образовывать как толпу, так и коллектив? 3) Каковы эти условия?
Для ответа на поставленные вопросы обратимся к формулам (3.9), (3.12), (3.13), (3.6), описывающим динамику поведения совокупности индивидуумов. Начнем с первого вопроса. Из формулы (3.9) видно, что на интервалах времени
![]() (4.1)
(4.1)
процесс ![]() ,
описывающий динамику изменения состояния
совокупности индивидуумов, равен 0, т.е. эта
совокупность всегда образует толпу. Подставив в
(4.1) выражения ЛО
,
описывающий динамику изменения состояния
совокупности индивидуумов, равен 0, т.е. эта
совокупность всегда образует толпу. Подставив в
(4.1) выражения ЛО ![]() и
и ![]() из (3.12) и вычислив эти ЛО
согласно формулам (3.7), получим такие выражения
для интервалов времени, на которых изучаемая
совокупность индивидуумов всегда образует толпу
из (3.12) и вычислив эти ЛО
согласно формулам (3.7), получим такие выражения
для интервалов времени, на которых изучаемая
совокупность индивидуумов всегда образует толпу
![]() . (4.2)
. (4.2)
В этих выражениях ![]() - конъюнкция НЛ,
- конъюнкция НЛ, ![]() -
дизъюнкция НЛ, а ЛО
-
дизъюнкция НЛ, а ЛО ![]() и
и ![]() вычисляются по формулам
(3.7). Далее, из формулы (3.9) видно, что на интервалах
времени
вычисляются по формулам
(3.7). Далее, из формулы (3.9) видно, что на интервалах
времени
![]() , (4.3)
, (4.3)
если они не вырождены в точку, процесс ![]() изменения состояния
совокупности индивидуумов равен 1, т.е. эта
совокупность образует коллектив. В
промежуточных же интервалах, если они не
вырождены, этот процесс равен 0, т.е. изучаемая
совокупность образует толпу. Реально, в
зависимости от соотношения между элементами ЛО
изменения состояния
совокупности индивидуумов равен 1, т.е. эта
совокупность образует коллектив. В
промежуточных же интервалах, если они не
вырождены, этот процесс равен 0, т.е. изучаемая
совокупность образует толпу. Реально, в
зависимости от соотношения между элементами ЛО ![]() и
и ![]() (3.5) (т.е. между моментами
(3.5) (т.е. между моментами ![]() ,
, ![]() изменения
состояния различных индивидуумов
изменения
состояния различных индивидуумов ![]() ) получаются различные соотношения
между самими этими ЛО и в итоге – различные
соотношения между ЛО
) получаются различные соотношения
между самими этими ЛО и в итоге – различные
соотношения между ЛО ![]() и
и ![]() (3.12). Таким образом,
реально интервалы времени (4.3) и промежуточные
между ними интервалы могут быть как невырождены,
так и вырождены, причем в последнем случае
ситуация переходит в противоположную: коллектив
превращается в толпу, а толпа – в коллектив. В
итоге приходим к следующему выводу: в интервале
времени
(3.12). Таким образом,
реально интервалы времени (4.3) и промежуточные
между ними интервалы могут быть как невырождены,
так и вырождены, причем в последнем случае
ситуация переходит в противоположную: коллектив
превращается в толпу, а толпа – в коллектив. В
итоге приходим к следующему выводу: в интервале
времени
![]() (4.4)
(4.4)
совокупность индивидуумов, в
зависимости от условий, может образовывать как
коллектив, так и толпу. Подставив в (4.4) найденные
выше в (4.2) выражения для ЛО ![]() и
и ![]() , получим такое
выражение для интервала времени
, получим такое
выражение для интервала времени ![]()
![]() . (4.5)
. (4.5)
В (4.5) ![]() -
конъюнкция НЛ, а ЛО
-
конъюнкция НЛ, а ЛО ![]() и
и ![]() вычисляются по формулам
(3.7).
вычисляются по формулам
(3.7).
Интервалы времени (4.1), в которых совокупность индивидуумов всегда образует толпу, совместно с интервалом времени (4.4), в котором эта совокупность, в зависимости от условий, может образовывать коллектив или толпу, охватывает всю временную ось. Это означает, что третий тип временных интервалов – те, в которых совокупность индивидуумов всегда образует коллектив, не существует.
Найдем теперь условия, при которых
совокупность индивидуумов в интервалах времени
(4.3) (промежуточных между ними интервалах)
образует коллектив (толпу). Возьмем первый
интервал (4.3): ![]() . Для
существования в нем коллектива нужно, чтобы он
был невырожден, т.е. чтобы выполнялось условие
. Для
существования в нем коллектива нужно, чтобы он
был невырожден, т.е. чтобы выполнялось условие ![]() . Решая это неравенство НЛ
[8], с учетом того, что
. Решая это неравенство НЛ
[8], с учетом того, что ![]() ,
получим:
,
получим: ![]() . Аналогично
исследуются остальные интервалы (4.3); и мы
получаем следующий результат. Совокупность
индивидуумов образует в интервалах времени (4.3)
коллектив только при выполнении таких условий:
. Аналогично
исследуются остальные интервалы (4.3); и мы
получаем следующий результат. Совокупность
индивидуумов образует в интервалах времени (4.3)
коллектив только при выполнении таких условий:
Интервал 1 2 … ![]()
![]()
Условие ![]()
![]() …
…![]()
![]() , (4.6) в которых
ЛО
, (4.6) в которых
ЛО ![]() имеют вид,
определяемый формулами (3.12),(3.5), а число
имеют вид,
определяемый формулами (3.12),(3.5), а число ![]() вычисляется по формулам
(3.13),(3.6).
вычисляется по формулам
(3.13),(3.6).
Подобным же образом изучаются интервалы времени, промежуточные между интервалами (4.3), имеющие вид
![]() . (4.7)
. (4.7)
При этом получается следующий результат.
Совокупность индивидуумов образует в
интервалах времени (4.7) толпу только при
выполнении следующих условий, в которых ЛО ![]() и число
и число ![]() те же, что и в (4.6):
те же, что и в (4.6):
Интервал 1 2 … ![]()
Условие ![]()
![]() …
…![]() . (4.8)
. (4.8)
При этих условиях левые границы
интервалов упрощаются ![]() ,
,
![]() и т.д. Объединяя оба
полученных результата, приходим к следующему:
совокупность индивидуумов образует коллектив в
последовательных интервалах времени
и т.д. Объединяя оба
полученных результата, приходим к следующему:
совокупность индивидуумов образует коллектив в
последовательных интервалах времени
![]() (4.9)
(4.9)
и толпу в промежуточных интервалах времени
![]() (4.10)
(4.10)
при выполнении таких необходимых и достаточных условий:
![]() (4.11)
(4.11)
Здесь ЛО ![]() определяются
формулами (3.12), (3.5), а число
определяются
формулами (3.12), (3.5), а число ![]() - формулами (3.13), (3.6).
- формулами (3.13), (3.6).
Практически выгодно, чтобы
индивидуумы представляли коллектив, а не толпу,
во всем временном интервале, где это
теоретически возможно, так чтобы эти два
состояния не чередовались во времени. Таким
временным интервалом является интервал ![]() , определяемый формулой
(4.4). Совокупность индивидуумов образует
коллектив во всем временном интервале
, определяемый формулой
(4.4). Совокупность индивидуумов образует
коллектив во всем временном интервале ![]() при выполнении следующих
необходимых и достаточных условий:
при выполнении следующих
необходимых и достаточных условий:
![]() . (4.12)
. (4.12)
Здесь ЛО ![]() определяются
формулами (3.12), (3.5), а число
определяются
формулами (3.12), (3.5), а число ![]() - формулами (3.13), (3.6).
- формулами (3.13), (3.6).
Действительно, коллектив во всем
временном интервале ![]() образуется
только если все входящие в него временные
интервалы (4.3) не вырождены [т.е. выполнены условия
(4.6)], а все промежуточные между ними временные
интервалы (4.3) вырождены [т.е. выполнены условия,
дополнительные к условиям (4.8)]. Взяв пересечение
этих двух групп условий и выполнив необходимые
упрощения, получим приведенное утверждение.
образуется
только если все входящие в него временные
интервалы (4.3) не вырождены [т.е. выполнены условия
(4.6)], а все промежуточные между ними временные
интервалы (4.3) вырождены [т.е. выполнены условия,
дополнительные к условиям (4.8)]. Взяв пересечение
этих двух групп условий и выполнив необходимые
упрощения, получим приведенное утверждение.
Заметим, что условия (4.6), (4.8), (4.11), (4.12), представляют собой требования определенной временной взаимоупорядоченности интервалов одинаковых состояний индивидуумов, входящих в изучаемую совокупность.
Проведенное в статье исследование показывает большие возможности, которые открываются при использовании автоматно-логических методов для изучения процессов образования и исчезновения коллективов. Главное преимущество этих методов состоит в возможности аналитического изучения систем высокой размерности. Это позволяет решать разнообразные задачи, связанные с изучением коллективов: компактное представление, расчет, анализ и синтез – едиными методами, основанными на едином математическом аппарате непрерывной логики и логических определителей. Причем аппарат непрерывной логики благодаря развитой системе эквивалентных преобразований обеспечивает большую конструктивность указанных методов, а аппарат логических определителей позволяет преодолеть “проклятие размерности”. Полученные результаты означают, что любая совокупность индивидуумов, изменяющих свое состояние во времени, всегда имеет интервалы времени, в которых она представляет собой толпу, но не всегда – интервалы времени, в которых она представляет собой коллектив. Последнее гарантируется только при определенной временной взаимоупорядоченности интервалов одинаковых состояний индивидуумов.
Литература
РЕФЕРАТ
УДК 519.1 Левин В. И. Моделирование процессов образования коллектива из индивидуумов. Показано, что задача определения условий возникновения и исчезновения коллектива и задача нахождения отклика динамического автомата на заданные входные процессы эквивалентны. На этой основе построена автоматная модель коллектива. Для ее анализа использованы непрерывная логика и логические определители.
MODELING OF PROCESSES OF FORMING A GROUP FROM INDIVIDUALS
V. I. Levin
Shown equivalence of problem of determination of conditions to origin and disappearances of group and problem of finding of response dynamic automaton on given input processes. On this base offered dynamic modeling of group. Used unceasing logic and logical finders.
Работа поддержана грантом РФФИ № 99-06-80264
Поступила в редакцию 27.07.2001.