УДК 4.8

АВТОМАТИЧЕСКИЙ СИНТЕЗ СТРУКТУРИРОВАННЫХ ПРЕДЛОЖЕНИЙ

©2002 г. И. Н. Плашенкова

В качестве методов анализа и синтеза структурированных предложений естественного языка применимы элементы теории формальных грамматик и теории семантических сетей. Доказано, что формальную грамматику класса структурированных предложений можно заменить семантическим деревом.

Введение. Принцип "дружественности" предполагает, что компьютер в процессе общения с пользователем сам строит предложения, общаясь, в прямом смысле слова, разговаривая с ним. Причём делает он это не с помощью заранее заготовленных фраз (например, такого высказывания: "встревожен, взволнован, приму меры", которым отвечал на любую жалобу посетителя столовой робот-официант из фантастического романа), а путём составления осмысленных предложений, дающих ответ на поставленный вопрос. Достичь этой цели, означает – научить компьютер самостоятельно строить и понимать предложения естественного языка. Точно так же, как он "понимает" математический язык (т. е. выполняет задачи, сформулированные на этом формальном языке).

Напрашивается возражение – естественный язык необъятен: ограничено количество слов, а предложений из них можно составить бесконечно много. Поэтому его невозможно отобразить в ограниченной памяти машины. Однако для решения математических задач на множестве, скажем, целых чисел, вовсе не обязательно оперировать со всем этим множеством. Достаточно иметь подходящее для решения данной задачи его конечное подмножество. Представив в памяти компьютера это подмножество и задав алгоритмы выполнения операций над целыми числами, мы сможем получить автоматизированное решение поставленной задачи. Таким образом, при работе с формальным языком реализована идея выделения подмножества. Настоящая работа посвящена применению этой идеи к естественному языку.

Для выделения конечных подмножеств бесконечного множества предложений естественного языка используем метод ограничения контекста и структуры предложений.

Ограничить контекст означает ограничить множество слов (словосочетаний) и знаков препинания, из которых состоят предложения языка, т. е. множество символов языка или терминальных символов. Например, в предложении "треугольник, у которого все стороны равны, называется равносторонним" можно выделить такие символы: "треугольник", ",", "у которого". Как видно из этого примера, в качестве терминального символа можно рассматривать и слово, и сочетание слов. На ограниченном контексте будем рассматривать предложения с заданной структурой, которые назовём специфическими предложениями в специфическом контексте. Поставим перед собой задачу автоматизировать анализ и синтез таких предложений.

Рассмотрим два простых примера специфических предложений в специфическом контексте.

Пример 1. Специфические предложения – определения, специфический контекст – учебная дисциплина, например, если в качестве контекста рассмотреть школьный курс геометрии, получатся определения по геометрии.

Автоматизированный анализ – проверка правильности сформулированного учеником определения, а также поиск определений в заданном тексте;

Пример 2. В качестве специфических предложений рассмотрим пословицы с однотипной структурой на заданном контексте, который представляет собой определённый набор слов, частный случай – отдельный класс пословиц вида

Как аукнется, так и откликнется; Что посеешь, то и пожнёшь; Кого люблю, того казню.

Автоматизированный синтез – получение предложений, похожих на пословицы, например таких, как Что аукнется, то и откликнется.

Ограниченную структуру предложений на ограниченном контексте можно представить, используя теорию формальных грамматик [1] или теорию семантических сетей [3]. Анализ и синтез предложений с ограниченной структурой можно осуществить с помощью алгоритмов разбора и вывода. К специфическим предложениям естественного языка применимы те же методы, которые применялись к формальным языкам.

Покажем это на примере рассмотренного класса пословиц.

I. Формальная грамматика пословиц. Структуру и контекст класса предложений можно описать с помощью формальной грамматики. Составим формальную грамматику для рассмотренного выше типа пословиц: Как аукнется, так и откликнется; Что посеешь, то и пожнёшь; Кого люблю, того казню.

Каждая из этих пословиц состоит из четырёх частей, по две части в каждой половине, причём эти половины противопоставлены одна другой. Части, или сегменты, назовём h1, h2, t1, t2 (от head – голова, tail – хвост).

Например, для пословицы Кого люблю, того казню:

Сегменты с одинаковыми индексами являются парными, в нашем примере: кого–того, люблю–казню. На схеме парные сегменты соединены круглыми скобками. Пара h2–t2 – глаголы, состоящие в отношениях, близких к антонимичности. Поэтому, если при автоматическом синтезе пословицы в качестве сегмента h1 выбран символ Кого, то обязательно t1= того. И если h2 = люблю, то t2 = казню.

Для записи формальной грамматики используем нормальную форму Бэкуса-Наура [1].

Составим грамматику G данного класса пословиц. Каждая пословица класса состоит из "головы" и "хвоста". Поэтому первое правило грамматики будет выглядеть так:

<пословица>::=<голова>, <хвост>

Это правило читается следующим образом: пословица определяется как совокупность головы, запятой и хвоста. Каждая из частей "голова" и "хвост" состоит из двух сегментов. Отразим это в двух следующих правилах:

<голова> ::= <h1> <h2>

<хвост> ::= <t1> <t2>

Значения h1 и t1, h2 и t2 не произвольны, они связаны друг с другом. Фактически, выбрав значение для h1, мы тем самым выбираем значение и для t1. То же с парой h2 и t2. Решим проблему представления этой части структуры пословицы с помощью такой записи правил:

<h1> & <t1> ::= Как & так и | Где & там и | Сколько & столько и | Куда & оттуда и | Кто & тот и | Что & то и | Кого & того

<h2> & <t2> ::= аукнется & откликнется | посеешь & пожнёшь | люблю & казню| поведёшься & наберёшься | пьют & льют   ("&" читается как "и", "|" читается как "или").

Последнее правило означает, что для пары символов <h2> и <t2> можно выбрать в качестве значений одну из пар терминальных символов в правой части правила. Например, если <h2> при выводе пословицы заменяется на "аукнется", то <t2> заменяется на "откликнется".

Итак, грамматика G выглядит следующим образом:

<пословица> ::= <голова>, <хвост>

<голова> ::= <h1> <h2>

<хвост> ::= <t1> <t2>

<h1> & <t1> ::= Как & так и | Где & там и | Сколько & столько и | Куда & оттуда и | Кто & тот и | Что & то и | Кого & того

<h2> & <t2> ::= аукнется & откликнется | посеешь & пожнёшь | люблю & казню | поведёшься & наберёшься | пьют & льют

Вывод предложения – это последовательность строк, первая из которых – начальный символ (в данном случае <пословица>), последняя – предложение языка (в нашем случае пословица или предложение, похожее на пословицу). Причём каждая последующая строка получается из предыдущей путём однократной подстановки по правилам грамматики.

Пример 3. Вывод (синтез) пословицы "Кого люблю, того казню" по правилам грамматики G:

<пословица>

<голова>, <хвост>

<h1> <h2>, <хвост>

Кого <h2>, <хвост>

Кого люблю, <хвост>

Кого люблю, <t1> <t2>

Кого люблю, того <t2>

Кого люблю, того казню

Подстановка идёт слева направо, <h1> и <t1>, <h2> и <t2> замещаются парами в соответствии с правилами грамматики G.

II. Семантические сети и их связь с грамматикой. Прежде чем приступить к выявлению связи грамматики с сетями, напомним некоторые факты из теории графов.

Граф отображает элементарный состав заданной системы и структуру связей в этой системе. Например, структуру пословицы можно представить в виде следующего графа, называемого деревом непосредственных составляющих.

Пример 4. Дерево имеет вид

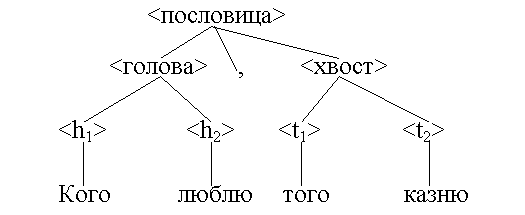
Символы "<пословица>", "<голова>", "," , "<хвост>" и т. д. представляют собой вершины графа. Рёбра графа изображаются в виде отрезков или стрелок, соединяющих вершины.

Деревом называется граф иерархической системы. Иерархическая система – это система, между элементами которой установлены отношения подчинения или вхождения друг в друга. Структура пословицы, представленная с помощью формальной грамматики, является иерархической системой: в <пословицу> "входят" символы "<голова>", "," , "<хвост>", символ "<голова>", в свою очередь, непосредственно составляют символы "<h1>" и "<h2>" и т. д. Поэтому граф, отображающий структуру предложения в соответствии с формальной грамматикой, можно назвать деревом непосредственных составляющих.

У графа, являющегося деревом, выделяют корень и листья. Начальный символ "<пословица>" помещается в корень дерева непосредственных составляющих, терминальные символы "Кого", "люблю", "," , "того", "казню" являются его листьями.

Вывод пословицы представляет собой движение по её дереву непосредственных составляющих сверху вниз.

Пример 5. Графическое представление вывода пословицы.

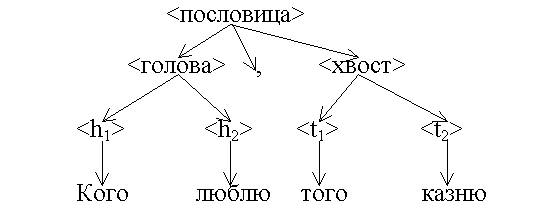
Граф из примера 4 является неориентированным, а граф, представленный в примере 5, ориентированный. В нём связи между вершинами изображаются в виде стрелок.

Неоднородная семантическая сеть – это ориентированный граф, вершины которого связаны несколькими отношениями.

Пример 6. Неоднородная семантическая сеть с двумя отношениями, соответствующая дереву непосредственных составляющих из примера 4.

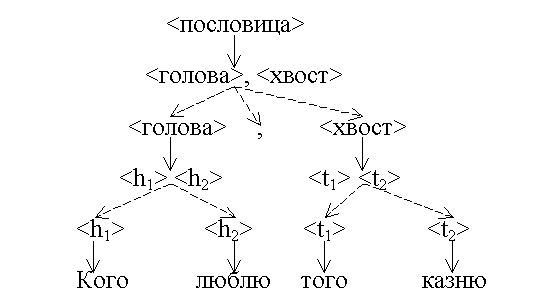
Неоднородную семантическую сеть такого вида будем называть семантическим деревом.

Дереву непосредственных составляющих соответствует семантическое дерево на множестве вершин дерева непосредственных составляющих. Это семантическое дерево имеет два отношения: включённости и непосредственной выводимости.

Определение 1. Строки A, B состоят в отношении непосредственной выводимости (B непосредственно выводится из A), если в грамматике существует правило, позволяющее заменить в строке A некоторую подстроку другой и получить в результате строку B.

Обозначим это отношение A ® B.

A ®B – ложное утверждение (B не выводится непосредственно из A), если в грамматике не существует такого правила.

Определение 2. Строки A, B состоят в отношении включённости (B включается в A), если строка B является подстрокой строки A. Обозначим отношение включённости A Й B.

"Прочитаем" семантическое дерево из примера 6 сверху вниз.

Из строки "<пословица>" выводима строка "<голова>, <хвост>". В строку "<голова>, <хвост>" включаются символы "<голова>", "," и "<хвост>". Из строки "<голова>" выводима строка "<h1> <h2>", в строку "<h1> <h2>" включаются символы "<h1>" и "<h2>" и т. д.

III. Вывод и разбор специфических предложений. Существуют алгоритмы вывода и разбора, позволяющие осуществить автоматизированный синтез и анализ предложений, структура и контекст которых заданы с помощью формальной грамматики.

Правила грамматики можно задать в виде таблицы значений функции C(B) = A, где A и B – строки, A ® B (т. е. в грамматике существует правило, позволяющее получить из строки A строку B за одну подстановку). Нескольким значениям аргументов будет соответствовать некоторое единственное значение C, поэтому мы имеем право назвать C функцией: в каждом правиле любой формальной грамматики единственная левая часть и одна или несколько правых частей, разделённых знаком "|".

Например,
C(<голова>, <хвост>) = <пословица>
C(Где & там и) = <h1> & <t1>
C(Кого & того) = <h1> & <t1>

Последняя строка означает, что одновременно C(Кого) = <h1> и C(того) = <t1>.

Описание алгоритма вывода.

  1. Найти множество аргументов, значение функции C от которых равно начальному символу. Заменить начальный символ одним из этих аргументов. Получится некоторая строка.
  2. Повторить операцию для крайнего левого символа полученной строки.
  3. Повторять, пока нельзя будет ничем заменить крайний левый символ. Далее повторить операцию для следующего слева символа.
  4. Повторять, пока все символы предложения не станут терминальными.

Разберём алгоритм вывода на примере вывода пословицы "Кого люблю, того казню".

Первая строка любого вывода – начальный символ. Итак, дана строка

<пословица>

Для грамматики пословиц G существует только один аргумент функции C, для которого значение C равно начальному символу: C(<голова>, <хвост>) = <пословица>. Заменим символ "<пословица>" на аргумент-строку "<голова>, <хвост>". Получим новую строку

<голова>, <хвост>

Согласно алгоритму, теперь будем работать с крайним левым символом строки – с символом "<голова>". У этого символа также единственный прообраз-аргумент функции C:

C(<h1> <h2>) = <голова>. Произведя соответствующую замену, получим строку

<h1> <h2>, <хвост>

Крайний левый символ "<h1>". У него множество прообразов. Выберем из них "Кого". C(Кого) = <h1>. Свойство рассматриваемой грамматики G – то, что теперь заранее известен прообраз ещё не появившегося в строке символа t1: C(того) = <t1>. Это пока не имеет значения. Производим текущую замену и получаем строку

Кого <h2>, <хвост>

Символ "Кого" ни на что не заменишь, он терминальный. Рассматриваем следующий слева символ "<h2>" и выбираем один из его прообразов – "люблю", C(люблю) = <h2>. Запоминаем, что прообразом t2 будет "казню". Подставив "люблю" вместо "<h2>", получим следующую строку вывода

Кого люблю, <хвост>

Следующий слева символ "," также терминальный, поэтому переходим к символу "<хвост>" и заменяем его на его единственный прообраз "<t1> <t2>":

Кого люблю, <t1> <t2>

Из оставшихся нетерминальных символов выбираем крайний левый. Прообраз "<t1>" был определён ранее. Это символ "того". Подставляем его:

Кого люблю, того <t2>

Переходим к следующему слева символу. Прообраз "<t2>" – символ "казню". Строка

Кого люблю, того казню

является последней строкой вывода, так как в ней все символы терминальные. Получили вывод пословицы из примера 3.

Разбор отличается от вывода тем, что идёт в обратном направлении – от предложения языка к начальному символу грамматики. Разбор используется для анализа предложений, т. е. для ответа на вопрос: принадлежит ли предложение грамматике.

Предложение считается принадлежащим данной грамматике тогда и только тогда, когда его можно вывести по правилам этой грамматики [1].

Позже мы докажем алгебраически, что семантические сети так же применимы для синтеза (анализа) предложений, заданных с помощью формальной грамматики, как и алгоритмы вывода (разбора).

IV. Равносильность моделей структуры специфических предложений. Докажем равносильность представлений структуры специфического предложения с помощью формальной грамматики, дерева непосредственных составляющих, вывода и разбора.

Лемма 1. Множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов и множество их выводов связывает взаимно однозначное соответствие.

Доказательство. Предложение, структуру которого можно представить с помощью формальной грамматики, принадлежит данной грамматике. А принадлежит оно данной грамматике тогда и только тогда, когда это предложение можно вывести по правилам грамматики из начального символа.

Т. к. вывод предложения отличается от разбора только направлением, то понятие "вывести" эквивалентно понятию "разобрать". Лемма доказана.

Лемма 2. Множество разборов предложений биективно отображается во множество их деревьев непосредственных составляющих.

Доказательство. Дерево непосредственных составляющих – это один из способов представления разбора предложения языка [1]. А это означает, что множество разборов и множество деревьев непосредственных составляющих связывает взаимно однозначное соответствие. Лемма доказана.

Следствие 1. Множества специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов, множество их выводов и множество их деревьев непосредственных составляющих связывает взаимно однозначное соответствие.

Доказательство вытекает из лемм 1 и 2 и свойств биекции.

Теорема 1. Каждому дереву непосредственных составляющих соответствует семантическое дерево с отношениями непосредственной выводимости и включённости, причём только одно.

Доказательство. Будем применять следующие обозначения:

A — B – в дереве непосредственных составляющих связаны вершины A и B, причём A изображается на дереве выше, чем B;

A ® B – B непосредственно выводится из A;

A Й B – B включается в A.

Пусть для символов A, B1, ..., Bn A — B1, A — B2, ... , A — Bn (B1, ..., Bn пронумерованы слева направо), причём не существует символа D, отличного от данных символов, такого, что A — D.

Найдём B = B1B2 ... Bn.

Теперь A ® B, B Й B1, B Й B2, ... , B Й Bn.

Таким образом, каждые n отношений дерева с общей начальной вершиной преобразуются в одно отношение непосредственной выводимости и n отношений включённости. Такое преобразование будет единственным, т. к. существует единственная упорядоченная конкатенация (т. е. объединение, сумма символов) B1B2 ... Bn.

Если A — B, где A, B – символы, то A ® B.

Т. к. дерево непосредственных составляющих можно рассматривать как совокупность рассмотренных отношений, то теорема доказана.

Следствие 2. Каждому специфическому предложению, структуру которого можно представить с помощью формальной грамматики, его разбору, выводу и его дереву непосредственных составляющих соответствует единственное семантическое дерево с отношениями непосредственной выводимости и включённости.

Доказательство следует из следствия 1 и теоремы 1.

Пример семантического дерева, соответствующего дереву непосредственных составляющих предложения, был представлен выше, в примере 6.

Ниже мы обобщим полученный результат: докажем алгебраически, что всю грамматику можно представить в виде семантического дерева. Для этого построим алгебры-модели грамматики и семантического дерева.

V. Модели грамматик. Покажем, что можно построить алгебру, соответствующую любой формальной грамматике.

Построим алгебру S = < S01, => > типа <2>. Она будет моделью формальной грамматики.

Рассмотрим множество S – множество всех строк, которые можно получить по правилам некоторой формальной грамматики. В этом множестве содержатся все строки вывода любого предложения грамматики.

Множество S01 = S И {0,1}

Определим операцию выводимости => на множестве S01.

Определение 3.

  1. для A, B О S
    A => B = 1, если A ® B;
    A => B = 0, если A ® B – ложное утверждение
  2. для A О S, B О {0,1}
    A => 0 = 0
    A => 1 = 0
    0 => A = 0
    1 => A = 0
  3. для A, B О {0,1}
    0 => 0 = 0
    0 => 1 = 0
    1 => 0 = 0
    1 => 1 = 0

Докажем, что алгебра S = < S01, => > является полугруппой.

Теорема 2. Операция => на множестве S01 является бинарной алгебраической ассоциативной операцией.

Доказательство. Согласно определению операции => на множестве S01, упорядоченной паре элементов множества S01 сопоставляется единственный элемент из множества {0,1} М S01. Следовательно, операция => бинарная, определённая на множестве S01. Для каждой упорядоченной пары элементов множества S01 определён результат операции =>. Этот результат также принадлежит множеству S01. Значит, операция => алгебраическая.

Докажем ассоциативность операции => на множестве S01, т. е. докажем, что (" A, B, C О S01) ((A => B) => C  =  A => (B => C)).
По определению операции =>, для любых A, B из множества S01 выполняется одно из двух:    A => B  =  0 или A => B   =  1.

Рассмотрим оба случая для левой части доказываемого равенства:

(A => B) => C  =  0 => С  =  0

(A => B) => C  =  1 => С  =  0 (по п. 2, 3 определения 3)

Для правой части:

A => (B => C)  = A => 0  =  0

A => (B => C)  =  A => 1  =  0 (по п. 2, 3 определения 3)

В любом случае, в левой и правой частях получаем 0. Следовательно, операция => ассоциативна.

Итак, операция => на множестве S01 является бинарной алгебраической ассоциативной операцией.

Следствие. Алгебра S = < S01, => > является полугруппой.

Доказательство. Полугруппа – это алгебра вида M = < M, * >, где * – бинарная алгебраическая ассоциативная операция на множестве M.

Из теоремы и из определения полугруппы следует, что алгебра S = < S01, => > является полугруппой.

Следствие доказано.

VI. Модель семантического дерева. Построим теперь модель семантического дерева на множестве подстрок, получаемых по правилам грамматики, с двумя отношениями: включённости и непосредственной выводимости. Этой моделью является алгебра
PS = < Ps01, Ю , Й > типа <2, 2>.

Обозначим через PS множество всех строк и подстрок, получаемых по правилам грамматики. В PS будут включаться, в частности, все терминальные и нетерминальные символы, встречающиеся в грамматике.

Пусть Ps01 = PS И {0,1}.

Определим на множестве Ps01 бинарные операции символьной выводимости Ю и включённости Й .

Отношение символьной непосредственной выводимости отличается от отношения непосредственной выводимости тем, что в выражении A ® B через A обозначается символ, а не строка:
для A, B О PS A ® B (B непосредственно выводится из A), если A – символ и в грамматике определений существует правило, позволяющее заменить символ A на строку B.

Отношение включённости определяется обычным образом.

Определение 4. Определение операции Ю на множестве Ps01:

  1. для A, B О PS
    A     Ю B = 1, если A ® B;
    A     Ю B = 0 в противном случае
  2. для A О PS, B О {0,1}
    A     Ю 0 = 0
    A     Ю 1 = 0
    0     Ю A = 0
    1     Ю A = 0
  3. для A, B О {0,1}
    0     Ю 0 = 0
    0     Ю 1 = 0
    1     Ю 0 = 0
    1     Ю 1 = 0

Определение 5. Определение операции Й на множестве Ps01:

  1. для A, B О PS  
    A     Й B = 1, если B М A;
    A     Й B = 0 в противном случае
  2. для A О PS , B О {0,1}
    A     Й 0 = 0
    A     Й 1 = 0
    0     Й A = 0
    1     Й A = 0
  3. для A, B О {0,1}
    0     Й 0 = 0
    0     Й 1 = 0
    1     Й 0 = 0
    1     Й 1 = 0

Аналогично доказывается, что операции Ю и Й являются бинарными алгебраическими операциями на множестве Ps01, алгебры Ps1 = <Ps01, Ю > и Ps2 = <Ps01, Й > являются полугруппами.

Алгебра PS = < Ps01, Ю , Й > является искомой моделью семантического дерева.

Для того чтобы установить связь между грамматикой и семантическим деревом, т. е. между полугруппой S = <S01, =>> и алгеброй PS = <Ps01, Ю , Й >, построим алгебру картежей элементов PS, алгебру Ps* = <Ps*01, Ю , Й > типа <2, 2>, Это будет надстройка над алгеброй PS, и следовательно, алгебра картежей также будет моделью семантического дерева.

Определение 6.

  1. Определим множество AS* как множество картежей вида
    (A1, A2,…, An), причём $ A’О S: A1 + A2 +…+ An = A’,
    A1, A2,…, An – символы из PS, n – любое натуральное число. Будем обозначать картеж (A1, A2,…, An) через A.
  2. BS* – множество картежей вида (B1, B2,…, Bn), причём
    $ B’О S: B1 + B2 +…+ Bn = B’ и $ A’О S: A’ => B’ = 1,
    B1, B2,…, Bn     О PS, n – любое натуральное число. Будем обозначать картеж                     (B1, B2,…, Bn) через B.
  3. PS* = AS* И BS*
    PS*01 = PS*     И {0,1}

Заметим, что для любого картежа A О PS* существует соответствующая ему строка A’О S (по определению множеств AS* и BS*).

Определение 7. Определение операции Ю на множестве PS*01:

для A, B О PS*01 A Ю B = A’ =>B’

Определение 8. Определение операции Й на множестве PS*01:

  1. для A, B О PS*
    A     Й B = 1, если конкатенация всех строк, составляющих картеж B, равна строке A’;
    A     Й B = 0 в противном случае
  2. для A О PS*, B О {0,1}
    A     Й 0 = 0
    A     Й 1 = 0
    0     Й A = 0
    1     Й A = 0
  3. для A, B О {0,1}
    0     Й 0 = 0
    0     Й 1 = 0
    1     Й 0 = 0
    1     Й 1 = 0

Можно доказать, что операции Ю и Й являются бинарными алгебраическими операциями на множестве Ps*01 и что алгебры
Ps*1 = <Ps*01, Ю > и Ps*2 = <Ps*01, Й > являются полугруппами.

Утверждение. Для любых картежей A, B О PS* A Й B = 1 тогда и только тогда, когда A’ = B’.

Доказательство. По определению 8   A Й B = 1 тогда и только тогда, когда конкатенация всех строк, составляющих картеж B, равна A’. Т. е. B = (B1, B2,…, Bn), B1 + B2 +…+ Bn = A’. Следовательно, по определению 6 строки A’, B’ равны.

Замечание. Доказанное утверждение избавляет нас от необходимости рассматривать операцию включённости. Эта операция "растворилась" во множестве картежей PS*. Достаточно изучить полугруппу <Ps*01, Ю >. Эта полугруппа и есть искомая модель семантического дерева на множестве подстрок, получаемых по правилам грамматики, с двумя отношениями: включённости и непосредственной выводимости.

VII. Гомоморфизм полугрупп строк и подстрок, порождаемых грамматикой. Известно, что отображение f алгебры <M1, +> в алгебру <M2, Е > является гомоморфизмом, если f – функция, сохраняющая алгебраическую операцию:
(" A,B О M1) (f (A + B) = f (A) Е f (B)).

Теорема 3. Полугруппы S = < S01, => > и Ps*1 = < Ps*01, Ю > гомоморфны.

Доказательство. Рассмотрим отображение f: Ps*01 ® S01 , определённое следующим образом. Каждому картежу
C = (C1, C2,…,Cn) О PS* ставится в соответствие строка C’’ О S,
f (0) = 0, f (1) = 1.

Докажем, что f – функция, т. е. что
(" CО Ps*01) ($! C’’ О S01) (C’’ = f (C)).

Пусть C О {0,1}. Тогда C’’ определяется однозначно по определению отображения f.

Пусть C О PS*. C = (C1, C2,…,Cn) и по определению 6 множества PS* C’ = C1 + C2 +…+ Cn. Для любой последовательности строк существует их конкатенация, причём единственная.

C’ = C’’. Теперь будем обозначать образ картежа C О Ps*01 при отображении f через C’.

Докажем, что (" A, B О Ps*01) (f (A Ю B) = f (A) => f(B)).

Нужно доказать, что f (A Ю B) = A’ => B’, где A, B – картежи, A’, B’ – соответствующие им строки.

Возможно 2 случая: A Ю B = 1 или A Ю B = 0.

При A Ю B = 1 f (A Ю B) = f (1) = 1 (по определению f)

A’ => B’  =  A Ю B  =  1 (по определению 7 операции Ю )

Значит, в этом случае f (A Ю B)  =  A’ => B’.

При A Ю B = 0   f (A ЮB) = f (0) = 0 (по определению f)

A’ => B’  =  A Ю B  =  0 (по определению 7 операции Ю )

Значит, в этом случае f (A Ю B)  =  A’=>B’.

Итак, для любых A, B О Ps*01 f (A Ю B) = A’ => B’ , т. е.
f (A Ю B) = f (A) => f (B).

Мы доказали, что отображение f: Ps*01 ® S01 является гомоморфизмом полугрупп S = <S01, => > и Ps*1 = <Ps*01, Ю >. Следовательно, эти полугруппы гомоморфны.

Теорема доказана.

Так как полугруппы S = <S01, => > и Ps*1 = <Ps*01, Ю > являются моделями грамматики и семантического дерева, то теорему 3 можно сформулировать следующим образом.

Теорема 3’. Любой формальной грамматике соответствует единственное семантическое дерево на множестве всех подстрок, порождаемых грамматикой, с двумя отношениями: непосредственной выводимости и включённости.

Заключение. Мы применили в качестве методов анализа и синтеза предложений естественного языка элементы теории формальных грамматик и теории семантических сетей. Выяснилось, что эти методы работы с формальными языками применимы к ограниченным областям естественных языков.

На примере одной из областей естественного языка был показан способ построения формальной грамматики и представлены различные модели структуры предложения естественного языка, выводимого по правилам формальной грамматики. Можно сказать, что структура одного предложения является частью формальной грамматики, которой это предложение принадлежит. Поэтому существуют аналогичные модели формальной грамматики в целом. В общем случае была доказана равносильность рассмотренных моделей формальной грамматики.

Кроме того, нами доказано, что методы из теории формальных грамматик (построение грамматики и её моделей) можно заменить методами из теории семантических сетей: любой формальной грамматике соответствует единственное семантическое дерево. Анализ и синтез предложений естественного языка, представляемых с помощью формальной грамматики, можно осуществлять, применяя как алгоритмы разбора и вывода, так и методы работы с семантическими сетями.

Литература

  1. Маккиман У., Хорнинг Дж., Уортман Д. Генератор компиляторов. Под ред. В.М. Савинкова. – М.: Статистика, 1980.
  2. Баевский В.С. Лингвистические, математические, семиотические и компьютерные модели в истории и теории литературы. – М.: Языки славянской культуры, 2001.
  3. Осипов Г.С. Приобретение знаний интеллектуальными системами: основы теории и технологии. – М.: Наука, Физматлит, 1997.

AUTOMATIC SYNTHESIS OF STRUCTURAL SENTENCES

Elements of formal grammars theory and semantic nets theory find a use for analysis and synthesis of natural language structural sentences. It proved, that a formal grammar of structural sentences class may be replaced by a semantic tree.

Смоленская гимназия им. Н.М. Пржевальского,
e-mail: pin@sci.smolensk.ru

Поступила в редакцию 8.10.2002.