УДК 4.8
ГОМОМОРФИЗМ АЛГЕБР-МОДЕЛЕЙ КОНТЕКСТНО-СВОБОДНЫХ ПОДМНОЖЕСТВ ЕСТЕСТВЕННЫХ ЯЗЫКОВ
© 2003 г. И. Н. Плашенкова
Для построения контекстно-свободных подмножеств естественных языков применимы элементы теории формальных грамматик и теории семантических сетей. Созданы алгебры-модели формальной грамматики и семантического дерева и доказано, что эти алгебры гомоморфны.
Введение. Рассмотрим задачу алгоритмизации распознавания и построения предложений естественного языка. Под распознаванием понимается ответ на вопрос: принадлежит ли некоторое предложение языку, т. е. удовлетворяет ли оно правилам языка. Построить предложение естественного языка означает получить предложение, принадлежащее этому языку.
Применительно к естественному языку в целом эта задача неразрешима, потому что в любом естественном языке (английском, русском и т. п.) большое множество слов и очень много вариантов структуры предложений (разные виды простых и сложных предложений). Возможно лишь частичное решение задачи путём построения контекстно-свободных подмножеств естественных языков. Т. е., если рассматривать не естественный язык в целом, а его подмножество со строго определёнными видами структуры предложений на ограниченном контексте, то выполнимо построение (синтез) и распознавание (анализ) предложений, удовлетворяющих установленным требованиям.
Решив задачу алгоритмизации распознавания и построения предложений, можно применить разработанные алгоритмы при создании прикладных программ в области педагогики. Приведём несколько примеров подобных программ.
В пределах урока учителю трудно проконтролировать усвоение определений всеми учащимися. Поэтому нужно автоматизировать проверку знаний. Существуют программы-тесты, предлагающие выбрать правильный вариант из предложенных. Но такие программы несовершенны. Для лучшего понимания материала ученик должен сам сформулировать ответ на поставленный вопрос.
С помощью алгоритма распознавания компьютер сможет определить, правильный дан ответ или нет, и если нет, указать, где ошибка, и дать соответствующий контрпример.
Некоторым учащимся трудно даётся составление своих примеров предложений по русскому языку. Например, дано задание: привести пример сложно-подчинённого предложения с придаточным времени. С помощью алгоритма построения предложений естественного языка учебная программа составляет несогласованное предложение с заданной структурой (к примеру, все глаголы в инфинитиве, все прилагательные мужского рода), и пользователю остаётся "причесать" полученное предложение.
Определения имеют ограниченное множество видов структуры. Значит, с помощью алгоритма распознавания можно найти нужное определение среди множества предложений.
Тот же принцип можно применить к поиску в сети Internet: добавить к поиску вхождений слов и фраз поиск определённых структур предложений и текстов.
Построение контекстно-свободных подмножеств естественных языков можно осуществить, используя теорию формальных грамматик [1] или теорию семантических сетей [3]. Это будет доказано алгебраически: мы докажем, что алгебры-модели формальной грамматики и семантического дерева любого контекстно-свободного подмножества естественного языка гомоморфны.
I. Построение контекстно-свободных подмножеств естественных языков. Для того чтобы построить контекстно-свободное подмножество естественного языка, нужно описать структуру предложений-элементов этого подмножества и символы языка, используемые для построения предложений подмножества. Под символами языка (терминальными символами) понимаются слова, словосочетания и знаки препинания, из которых состоят предложения языка. Множество всех таких терминальных символов также будем называть контекстом выбранного класса предложений.
Структуру и контекст класса предложений можно описать с помощью формальной грамматики.
Для записи формальной грамматики используем нормальную форму Бэкуса-Наура [1].
В естественном языке есть группы символов, функционирующих как единое целое. Например, группа символов "ограниченная с двух сторон" в предложении "отрезок – это часть прямой, ограниченная с двух сторон" объединяется в один символ – причастный оборот. Такие символы будем называть нетерминальными символами высокого уровня.
Существуют нетерминальные символы первого уровня, которые определяются через терминальные символы. Например, нетерминальный символ <существительное> определяется как терминальный символ ‘часть’ или как терминальный символ ‘отрезок’.
Пример 1. Нетерминальные символы высокого уровня формальной грамматики пословиц вида Как аукнется, так и откликнется; Что посеешь, то и пожнёшь; Кого люблю, того казню определяются следующими правилами:
<пословица> ::= <голова>, <хвост>
<голова> ::= <h1> <h2>
<хвост> ::= <t1> <t2>
Построение данной грамматики и правила, определяющие нетерминальные символы первого уровня, см. в [4].
Вывод предложения – это последовательность строк, первая из которых – начальный символ, последняя – предложение языка. Причём каждая последующая строка получается из предыдущей путём однократной подстановки по правилам грамматики.
Пример 2. Вывод (синтез) пословицы Кого люблю, того казню.
<пословица>
<голова>, <хвост>
<h1> <h2>, <хвост>
Кого <h2>, <хвост>
Кого люблю, <хвост>
Кого люблю, <t1> <t2>
Кого люблю, того <t2>
Кого люблю, того казню
Любую формальную грамматику можно представить в виде множества выводов всех предложений, принадлежащих грамматике. Ниже это будет доказано.
Деревом называется граф иерархической системы. Иерархическая система – это система, между элементами которой установлены отношения подчинения или вхождения друг в друга.
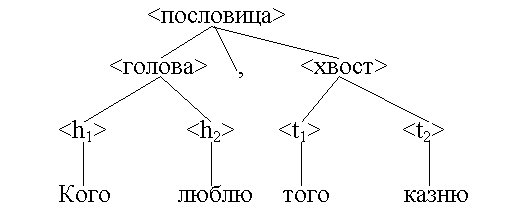
Пример 3. Структуру пословицы Кого люблю, того казню можно представить в виде следующего графа.

Структура пословицы, представленная с помощью формальной грамматики, является иерархической системой: в <пословицу> "входят" символы "<голова>", "," , "<хвост>", символ "<голова>", в свою очередь, непосредственно составляют символы "<h1>" и "<h2>" и т. д. Поэтому граф, отображающий структуру предложения в соответствии с формальной грамматикой, можно назвать деревом непосредственных составляющих.
Вывод предложения представляет собой движение по его дереву непосредственных составляющих сверху вниз.
Множество деревьев непосредственных составляющих всех предложений, принадлежащих грамматике, и множество выводов всех предложений грамматики связаны взаимно-однозначным соответствием. Позже это будет доказано.
К построению контекстно-независимых подмножеств естественных языков, кроме теории формальных грамматик, можно применить теорию семантических сетей. Доказательство этого утверждения будет приведено ниже.
Неоднородная семантическая сеть – это ориентированный граф, вершины которого связаны несколькими отношениями.
Пример 4. Неоднородная семантическая сеть с двумя отношениями, соответствующая дереву непосредственных составляющих из примера 3.
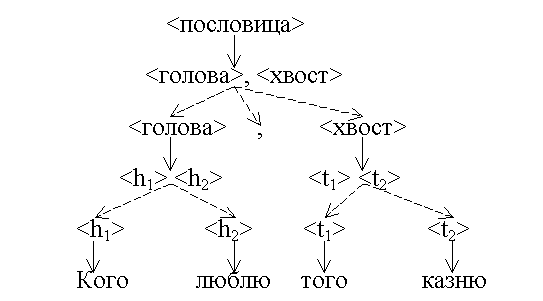
Неоднородную семантическую сеть такого вида будем называть семантическим деревом.
Дереву непосредственных составляющих соответствует семантическое дерево на множестве вершин дерева непосредственных составляющих. Это семантическое дерево имеет два отношения: включённости и непосредственной выводимости.
Определение 1. Строки A, B состоят в отношении непосредственной выводимости (B непосредственно выводится из A), если в грамматике существует правило, позволяющее заменить в строке A некоторую подстроку другой и получить в результате строку B.
Обозначим это отношение A
® B.A
® B – ложное утверждение (B не выводится непосредственно из A), если в грамматике не существует такого правила.Определение 2. Строки A, B состоят в отношении включённости (B включается в A), если строка B является подстрокой строки A.
Обозначим отношение включённости A
Й B.Существуют алгоритмы вывода и разбора, позволяющие осуществить автоматизированный синтез и анализ предложений, являющихся элементами контекстно-независимых подмножеств естественных языков.
Правила грамматики можно задать в виде таблицы значений функции C(B) = A, где A и B – строки, A
® B (т. е. в грамматике существует правило, позволяющее получить из строки A строку B за одну подстановку). Нескольким значениям аргументов будет соответствовать некоторое единственное значение C, поэтому мы имеем право назвать C функцией: в каждом правиле любой формальной грамматики единственная левая часть и одна или несколько правых частей, разделённых знаком "|".Например,
C(<голова>, <хвост>) = <пословица>
C(<h1> <h2>) = <голова>
C(<t1> <t2>) = <хвост>
Описание алгоритма вывода.
Разбор отличается от вывода тем, что идёт в обратном направлении – от предложения языка к начальному символу грамматики.
Описание алгоритма разбора.
Пусть A, B – строки, причём B – строка, состоящая из терминальных символов. Начальные значения: A – пустая строка, B – разбираемое предложение.
Повторять, пока строка A не станет равной начальному символу:
Иначе перейти к п. 2.
Иначе перейти к п. 1.
Разбор используется для анализа предложений, т. е. для ответа на вопрос: принадлежит ли предложение грамматике. Предложение считается принадлежащим данной грамматике тогда и только тогда, когда его можно вывести по правилам этой грамматики [1].
Алгоритм разбора конечен только в том случае, если разбираемое предложение принадлежит грамматике, т. е. если можно получить в строке A начальный символ грамматики. Однако этот алгоритм легко изменить для решения вопроса о принадлежности предложения формальной грамматике.
При "зацикливании" алгоритма у строки A получается два одинаковых значения подряд. Остаётся завести дополнительное условие прекращения работы цикла: равенство предыдущего и текущего значений строки A. Если выход из цикла произошёл при A, равном начальному символу грамматики, то разбираемое предложение принадлежит ей. Если же после выхода из цикла A не совпадает с начальным символом, то предложение грамматике не принадлежит.
Мы докажем алгебраически, что семантические сети так же применимы для синтеза (анализа) предложений, заданных с помощью формальной грамматики, как и алгоритмы вывода (разбора).
II. Равносильность моделей структуры предложений, принадлежащих контекстно-свободным подмножествам естественных языков. Будем называть указанные предложения специфическими. Докажем равносильность представлений структуры специфических предложений с помощью формальной грамматики, дерева непосредственных составляющих, вывода и разбора.
Лемма 1. Множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов и множество их выводов связывает взаимно однозначное соответствие.
Доказательство. Предложение, структуру которого можно представить с помощью формальной грамматики, принадлежит данной грамматике. А принадлежит оно данной грамматике тогда и только тогда, когда это предложение можно вывести по правилам грамматики из начального символа.
Т. к. вывод предложения отличается от разбора только направлением, то понятие "вывести" эквивалентно понятию "разобрать". Лемма доказана.
Лемма 2. Множество разборов предложений биективно отображается во множество их деревьев непосредственных составляющих.
Доказательство. Дерево непосредственных составляющих – это один из способов представления разбора предложения языка [1]. А это означает, что множество разборов и множество деревьев непосредственных составляющих связывает взаимно однозначное соответствие. Лемма доказана.
Следствие 1. Множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов, множество их выводов и множество их деревьев непосредственных составляющих связывает взаимно однозначное соответствие.
Доказательство. Согласно лемме 1, множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов и множество их выводов связывает биекция.
По лемме 2, множество разборов предложений биективно отображается во множество их деревьев непосредственных составляющих.
Взаимно однозначное соответствие, как известно, обладает свойством транзитивности, т. е., если множество A биективно отображается на множество B, а множества B и C также связывает взаимно однозначное отношение, то множество A биективно отображается на множество C.
Следовательно, множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов, множество их выводов и множество их деревьев непосредственных составляющих связывает взаимно однозначное соответствие.
Следствие доказано.
Теорема 1. Каждому дереву непосредственных составляющих соответствует семантическое дерево с отношениями непосредственной выводимости и включённости, причём только одно.
Доказательство. Будем применять следующие обозначения:
A — B – в дереве непосредственных составляющих связаны вершины A и B, причём A изображается на дереве выше, чем B;
A
® B – B непосредственно выводится из A;A
Й B – B включается в A.Пусть для символов A, B1, ..., Bn A — B1, A — B2, ... , A — Bn (B1, ..., Bn пронумерованы слева направо), причём не существует символа D, отличного от данных символов, такого, что A — D.
Найдём B = B1B2 ... Bn.
Теперь A
® B, B Й B1, B Й B2, ... , B Й Bn.Таким образом, каждые n отношений дерева с общей начальной вершиной преобразуются в одно отношение непосредственной выводимости и n отношений включённости. Такое преобразование будет единственным, т. к. существует единственная упорядоченная конкатенация (т. е. объединение, сумма символов) B1B2 ... Bn.
Если A — B, где A, B – символы, то A
® B.Т. к. дерево непосредственных составляющих можно рассматривать как совокупность рассмотренных отношений, то теорема доказана.
Следствие 2. Каждому специфическому предложению, структуру которого можно представить с помощью формальной грамматики, его разбору, выводу и его дереву непосредственных составляющих соответствует единственное семантическое дерево с отношениями непосредственной выводимости и включённости.
Доказательство. По теореме 1, каждому дереву непосредственных составляющих соответствует семантическое дерево с отношениями непосредственной выводимости и включённости, причём только одно.
Согласно следствию 1, множество специфических предложений, структура которых представима с помощью формальной грамматики, множество их разборов, множество их выводов и множество их деревьев непосредственных составляющих связывает взаимно однозначное соответствие.
Следовательно, каждому специфическому предложению, структуру которого можно представить с помощью формальной грамматики, его разбору, выводу и его дереву непосредственных составляющих соответствует единственное семантическое дерево с отношениями непосредственной выводимости и включённости.
Следствие доказано.
Пример семантического дерева, соответствующего дереву непосредственных составляющих предложения, был представлен выше, в примере 6.
Ниже мы обобщим полученный результат: докажем алгебраически, что всю грамматику можно представить в виде семантического дерева. Для этого построим алгебры-модели грамматики и семантического дерева.
III. Модели грамматик. Покажем, что можно построить алгебру, соответствующую любой формальной грамматике.
Построим алгебру S = < S01, => > типа <2>. Она будет моделью формальной грамматики.
Рассмотрим множество S – множество всех строк, которые можно получить по правилам некоторой формальной грамматики. В этом множестве содержатся все строки вывода любого предложения грамматики.
Множество S01 = S
И {0,1}Определим операцию выводимости => на множестве S01.
Определение 3.
Докажем, что алгебра S = < S01, => > является полугруппой.
Теорема 2. Операция => на множестве S01 является бинарной алгебраической ассоциативной операцией.
Доказательство. Согласно определению операции => на множестве S01, упорядоченной паре элементов множества S01 сопоставляется единственный элемент из множества {0,1}
О S01. Следовательно, операция => бинарная, определённая на множестве S01. Для каждой упорядоченной пары элементов множества S01 определён результат операции =>. Этот результат также принадлежит множеству S01. Значит, операция => алгебраическая.Докажем ассоциативность операции => на множестве S01, т. е. докажем, что (
" A, B, C О S01) ((A => B) => C = A => (B => C)).A => B = 0 или A => B = 1.
Рассмотрим оба случая для левой части доказываемого равенства:
(A => B) => C = 0 => С = 0
(A => B) => C = 1 => С = 0 (по п. 2, 3 определения 3)
Для правой части:
A => (B => C) = A => 0 = 0
A => (B => C) = A => 1 = 0 (по п. 2, 3 определения 3)
В любом случае, в левой и правой частях получаем 0. Следовательно, операция => ассоциативна.
Итак, операция => на множестве S01 является бинарной алгебраической ассоциативной операцией.
Следствие. Алгебра S = < S01, => > является полугруппой.
Доказательство. Полугруппа – это
алгебра вида M = < M, * >,
где * – бинарная алгебраическая ассоциативная
операция на множестве M.
Из теоремы и из определения полугруппы следует, что алгебра S = < S01, => > является полугруппой.
Следствие доказано.
IV. Модель семантического дерева. Построим теперь модель семантического дерева на множестве подстрок, получаемых по правилам грамматики, с двумя отношениями: включённости и непосредственной выводимости. Этой моделью является алгебра
PS = < Ps01, Ю , Й > типа <2, 2>.
Обозначим через PS множество всех строк и подстрок, получаемых по правилам грамматики. В PS будут включаться, в частности, все терминальные и нетерминальные символы (первого и высокого уровней), встречающиеся в грамматике.
Пусть Ps01 = PS
И {0,1}.Определим на множестве Ps01 бинарные операции символьной выводимости
Ю и включённости Й .Отношение символьной непосредственной выводимости отличается от отношения непосредственной выводимости тем, что в выражении A
® B через A обозначается символ, а не строка: для A, B О PS A ® B (B непосредственно выводится из A), если A – символ и в грамматике определений существует правило, позволяющее заменить символ A на строку B.Отношение включённости определяется обычным образом: строки A, B состоят в отношении включённости (B включается в A), если строка B является подстрокой строки A. Обозначение: A
Й B.Определение 4. Определение операции
Ю на множестве Ps01:Определение 5. Определение операции
Й на множестве Ps01:Аналогично доказывается, что операции
Ю и Й являются бинарными алгебраическими операциями на множестве Ps01, алгебры Ps1 = <Ps01, Ю > и Ps2 = <Ps01, Й > являются полугруппами.Алгебра PS = < Ps01,
Ю , Й > является искомой моделью семантического дерева.Для того чтобы установить связь между грамматикой и семантическим деревом, т. е. между полугруппой S = <S01, =>> и алгеброй PS = <Ps01,
Ю , Й >, построим алгебру картежей элементов PS, алгебру Ps* = <Ps*01, Ю , Й > типа <2, 2>, Это будет надстройка над алгеброй PS, и следовательно, алгебра картежей также будет моделью семантического дерева.Определение 6.
A1, A2,…, An – символы из PS, n – любое натуральное число. Будем обозначать картеж (A1, A2,…, An) через A.
Заметим, что для любого картежа A
О PS* существует соответствующая ему строка A’О S (по определению множеств AS* и BS*).Определение 7. Определение операции
Ю на множестве PS*01:для A, B
О PS*01 A Ю B = A’ =>B’Определение 8. Определение операции
Й на множестве PS*01:Можно доказать, что операции
Ю и Й являются бинарными алгебраическими операциями на множестве Ps*01 и что алгебрыPs*1 = <Ps*01,
Ю > и Ps*2 = <Ps*01, Й >являются полугруппами.
Утверждение. Для любых картежей A, B
О PS* A Й B = 1 тогда и только тогда, когда A’ = B’.Доказательство. По определению 8 A
Й B = 1 тогда и только тогда, когда конкатенация всех строк, составляющих картеж B, равна A’. Т. е. B = (B1, B2,…, Bn), B1 + B2 +…+ Bn = A’. Следовательно, по определению 6 строки A’, B’ равны.Замечание. Доказанное утверждение избавляет нас от необходимости рассматривать операцию включённости. Эта операция "растворилась" во множестве картежей PS*. Достаточно изучить полугруппу <Ps*01,
Ю >. Эта полугруппа и есть искомая модель семантического дерева на множестве подстрок, получаемых по правилам грамматики, с двумя отношениями: включённости и непосредственной выводимости.V. Гомоморфизм полугрупп строк и подстрок, порождаемых грамматикой. Известно, что отображение f алгебры <M1, +> в алгебру <M2,
Е > является гомоморфизмом, если f – функция, сохраняющая алгебраическую операцию:(
" A, B О M1) (f (A + B) = f (A) Е f (B)).Теорема 3. Полугруппы S = < S01, => > и Ps*1 = < Ps*01, Ю > гомоморфны.
Доказательство. Рассмотрим отображение f:
Ps*01 ® S01
, определённое следующим образом. Каждому
картежу
C = (C1, C2,…,Cn) О PS* ставится в
соответствие строка C’’ О
S,
f (0) = 0, f (1) = 1.
Докажем, что f – функция, т. е. что
(" CО
Ps*01) ($! C’’
О S01) (C’’ = f (C)).
Пусть C О {0,1}. Тогда C’’ определяется однозначно по определению отображения f.
Пусть C О PS*. C = (C1, C2,…,Cn) и по определению 6 множества PS* C’ = C1 + C2 +…+ Cn. Для любой последовательности строк существует их конкатенация, причём единственная.
C’ = C’’. Теперь будем обозначать образ картежа C О Ps*01 при отображении f через C’.
Докажем, что (" A, B О Ps*01) (f (A Ю B) = f (A) => f(B)).
Нужно доказать, что f (A Ю B) = A’ => B’, где A, B – картежи, A’, B’ – соответствующие им строки.
Возможно 2 случая: A Ю B = 1 или A Ю B = 0.
При A Ю B = 1 f (A Ю B) = f (1) = 1 (по определению f)
A’ => B’ = A Ю B = 1 (по определению 7 операции Ю )
Значит, в этом случае f (A Ю B) = A’ => B’.
При A Ю B = 0 f (A ЮB) = f (0) = 0 (по определению f)
A’ => B’ = A Ю B = 0 (по определению 7 операции Ю )
Значит, в этом случае f (A Ю B) = A’=>B’.
Итак, для любых A, B О Ps*01
f (A Ю B) = A’ => B’
, т. е.
f (A Ю B) = f (A)
=> f (B).
Мы доказали, что отображение f: Ps*01 ® S01 является гомоморфизмом полугрупп S = <S01, => > и Ps*1 = <Ps*01, Ю >. Следовательно, эти полугруппы гомоморфны.
Теорема доказана.
Так как полугруппы S = <S01, => > и Ps*1 = <Ps*01,
Ю > являются моделями грамматики и семантического дерева, то теорему 3 можно сформулировать следующим образом.Теорема 3’. Любой формальной грамматике соответствует единственное семантическое дерево на множестве всех подстрок, порождаемых грамматикой, с двумя отношениями: непосредственной выводимости и включённости.
Заключение. Мы рассмотрели различные способы представления контекстно-свободных подмножеств естественных языков:
множество деревьев непосредственных составляющих всех предложений, принадлежащих контекстно-свободному подмножеству;
множество разборов всех предложений контекстно-свободного подмножества;
множество выводов всех предложений контекстно-свободного подмножества естественного языка;
множество семантических деревьев всех предложений-элементов контекстно-свободного подмножества естественного языка, объединённое в одно семантическое дерево.
Все перечисленные способы представления контекстно-свободных подмножеств являются их моделями. Мы доказали алгебраически равносильность первых четырёх моделей.
Были построены алгебры-модели формальной грамматики и семантического дерева. Доказано, что эти алгебры гомоморфны.
Другими словами, любой формальной грамматике соответствует единственное семантическое дерево на множестве всех подстрок, порождаемых грамматикой, с двумя отношениями: непосредственной выводимости и включённости.
Итак, нами доказано, что при построении контекстно-свободных подмножеств естественных языков можно применять как теорию формальных грамматик, так и теорию семантических сетей.
Литература
THE GOMOMORFISM OF ALGEBRAS-MODELS OF NATURAL LANGUAGE CONTEXT-FREE UNDERMULTITUDES
I. N. Plashenkova Elements of formal grammars theory and semantic nets theory find a use for natural language context-free undermultitudes construction. Algebras-models of formal grammar and semantic tree have been created, and it is proved, that these algebras are gomomorfed.Смоленская гимназия им. Н.М.
Пржевальского,
e-mail: pin@sci.smolensk.ru
Поступила в редакцию 28.01.2003.