УДК 519.21:621.396.969.1
НАХОЖДЕНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ ОЦЕНКИ УГЛОВОГО РАССОГЛАСОВАНИЯ ДЛЯ ОБЗОРНОЙ АМПЛИТУДНОЙ СУММАРНО–РАЗНОСТНОЙ МОНОИМПУЛЬСНОЙ СИСТЕМЫ
© 2003 г. С. А. Вашкевич
В результате проведенного статистического анализа обзорной амплитудной суммарно–разностной моноимпульсной системы получены аналитические выражения, описывающие плотность вероятности оценки модуля и знака углового рассогласования между равносигнальным направлением и направлением на объект для трех характерных случаев отношения сигнал–шум в приемных каналах системы: малые отношения в суммарном и разностном; большое – в суммарном, малое – в разностном; большое – в суммарном и разностном. Проведенный анализ позволил выявить основные недостатки данного измерителя.
Проанализированные в [1] показатели
качества оценки углового рассогласования (![]() ), получаемые на выходе
обзорной амплитудной моноимпульсной системы,
математическая модель которой представлена на
рис. 1, не в полной мере отражают качество
указанной оценки. Наиболее полной
характеристикой обладает апостериорная
плотность вероятности оцениваемого параметра,
нахождению которой и посвящена статья.
), получаемые на выходе
обзорной амплитудной моноимпульсной системы,
математическая модель которой представлена на
рис. 1, не в полной мере отражают качество
указанной оценки. Наиболее полной
характеристикой обладает апостериорная
плотность вероятности оцениваемого параметра,
нахождению которой и посвящена статья.
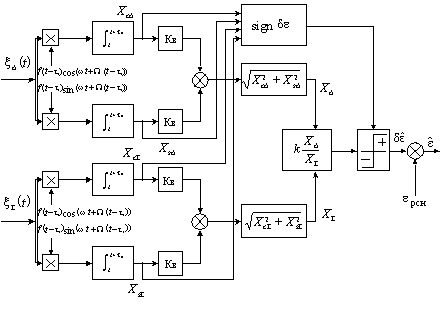
Рис. 1. Структурная схема математической модели обзорной МИ–системы
Оценка модуля | ![]() | формируется делением значения огибающей
сигнала в разностном канале на значение
огибающей в суммарном канале приемного тракта.
| формируется делением значения огибающей
сигнала в разностном канале на значение
огибающей в суммарном канале приемного тракта.
Известно [2], что распределение
вероятности огибающей смеси радиосигнала и
квазигармонического узкополосного случайного
процесса (шума) на выходе оптимального фильтра
подчиняется райсовскому закону, а выражение ее
плотности, записанное для безразмерных величин ![]() и
и ![]() (где
(где ![]() – значение
огибающей смеси сигнала и шума,
– значение
огибающей смеси сигнала и шума, ![]() – нормированное шумом значение амплитуды
сигнала, характеризующее отношение сигнал/шум по
напряжению,
– нормированное шумом значение амплитуды
сигнала, характеризующее отношение сигнал/шум по
напряжению, ![]() – амплитуда
эхосигнала, а
– амплитуда
эхосигнала, а ![]() – СКО
шума), имеет вид
– СКО
шума), имеет вид
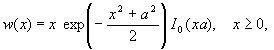 (1)
(1)
где ![]() – модифицированная функция Бесселя первого рода
нулевого порядка.
– модифицированная функция Бесселя первого рода
нулевого порядка.
Используя известные асимптотические представления функций Бесселя мнимого аргумента [3]:
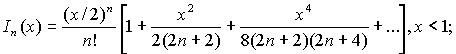
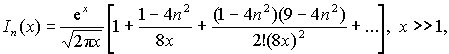
выражение (1) можно свести к следующим выражениям:
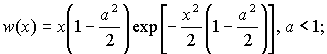 (2)
(2)
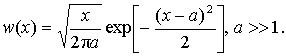 (3)
(3)
Если ![]() , то
вероятные значения
, то
вероятные значения ![]() будут сгруппированы около параметра
будут сгруппированы около параметра ![]() , т. е. с некоторым приближением можно
считать
, т. е. с некоторым приближением можно
считать ![]() . В этом случае
плотность вероятности огибающей будет близка к
нормальному закону распределения.
. В этом случае
плотность вероятности огибающей будет близка к
нормальному закону распределения.
Таким образом, для нахождения
плотности вероятности модуля углового
рассогласования (![]() )
необходимо найти ее для отношения двух случайных
величин, распределенных по закону Райса. Однако
получить в явном виде
)
необходимо найти ее для отношения двух случайных
величин, распределенных по закону Райса. Однако
получить в явном виде ![]() ,
оперируя выражением (1), достаточно трудно, а
полученное сложное математическое выражение
плохо поддается анализу и не в явном виде
отражает физические процессы, протекающие в
измерителе. Можно упростить решение
поставленной задачи, если воспользоваться для
описания плотности вероятности огибающих
,
оперируя выражением (1), достаточно трудно, а
полученное сложное математическое выражение
плохо поддается анализу и не в явном виде
отражает физические процессы, протекающие в
измерителе. Можно упростить решение
поставленной задачи, если воспользоваться для
описания плотности вероятности огибающих ![]()
Выясним, от чего зависит отношение сигнал/шум в суммарном и разностном каналах приемного тракта. Нормированная шумом амплитуда сигнала в каждом из каналов приемного тракта обзорной моноимпульсной РЛС описывается следующими выражениями:
![]() , (4)
, (4)
где ![]() – коэффициенты, учитывающие уровень диаграммы
направленности антенны (ДНА) в каналах;
– коэффициенты, учитывающие уровень диаграммы
направленности антенны (ДНА) в каналах;
![]() –
СКО шума в соответствующем канале.
–
СКО шума в соответствующем канале.
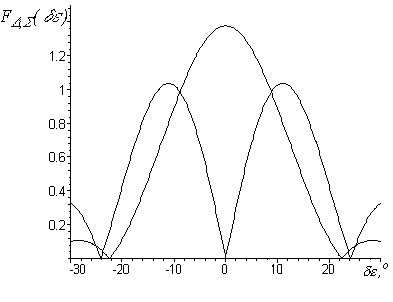
Рис. 2. ДНА амплитудной моноимпульсной системы
Из выражений (4) следует, что отношение сигнал/шум в каждом из каналов зависит от интенсивности эхосигнала, уровня ДНА и дисперсии шума в канале обработки. На рис. 2 показаны зависимости уровня ДНА от углового положения цели для обоих каналов.
Из анализа выражений (4) и графиков (рис. 2) следует, что при одних и тех же интенсивностях эхосигналов и дисперсиях шумов в каналах обработки отношение сигнал/шум будет разным.
Таким образом, в зависимости от величины углового рассогласования и уровня помех возможны три случая отношения сигнал/шум в каналах приемного тракта: малое отношение как в суммарном, так и разностном; большое отношение в суммарном и малое – в разностном; большое отношение как в суммарном, так и в разностном.
Найдем закон распределения ![]() для каждого из трех
вариантов, пользуясь известным выражением
функции распределения отношения двух случайных
величин [4]:
для каждого из трех
вариантов, пользуясь известным выражением
функции распределения отношения двух случайных
величин [4]:
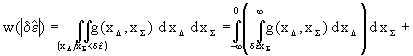
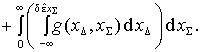 (5)
(5)
Учитывая, что область определения значений огибающей радиосигнала соответствует области неотрицательных чисел, выражение (5) можно переписать в виде
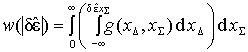 . (6)
. (6)
Дифференцируя выражение (6) по ![]() , найдем плотность
распределения вероятности
, найдем плотность
распределения вероятности ![]() :
:
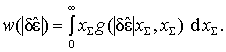 (7)
(7)
Поскольку суммарный и разностный каналы приемного тракта не имеют общих элементов, то случайные процессы, протекающие в них, можно считать независимыми. Тогда выражение (7) примет вид
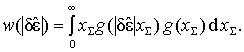 (8)
(8)
Для первого случая плотности
вероятности огибающих радиосигнала в суммарном
и разностном каналах приемного тракта
описываются выражением (2). Тогда плотность
вероятности ![]() на
основании выражения (8) и после проведения
несложных преобразований равна
на
основании выражения (8) и после проведения
несложных преобразований равна
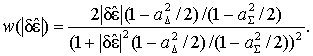 (9)
(9)
Для второго случая, когда плотность
вероятности огибающей радиосигнала в суммарном
канале описывается формулой (2), а в разностном –
формулой (3), выражение для плотности вероятности ![]() имеет вид
имеет вид
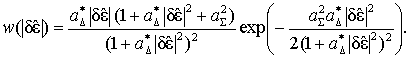 (10)
(10)
где ![]()
Для третьего случая, когда плотности
вероятности огибающих радиосигнала как в
суммарном, так и в разностном каналах приемного
тракта описываются формулой (3), выражение для
плотности вероятности ![]() можно записать в виде
можно записать в виде
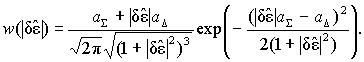 (11)
(11)
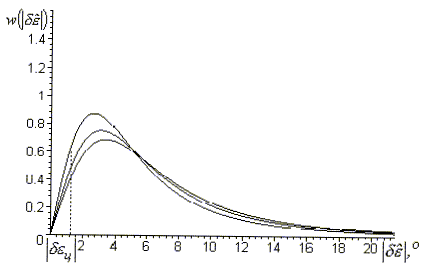
Рис. 3. Плотность распределения
вероятности ![]() для
первого случая
для
первого случая
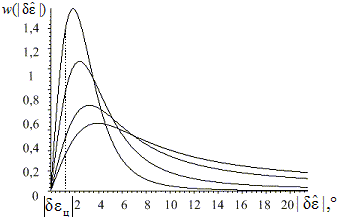
Рис. 4. Плотность распределения
вероятности ![]() для
второго случая
для
второго случая
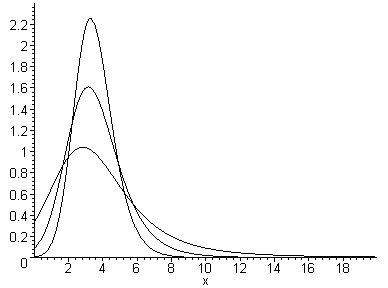
Рис. 5. Плотность распределения
вероятности ![]() для
третьего случая
для
третьего случая
Графики (рис. 3–5), построенные по
выражениям (9–11), дают наглядное представление о
законах распределения модуля оценки углового
рассогласования, формируемой измерителем, для
различных случаев отношения сигнал/шум в каналах
тракта обработки. В первых двух случаях (см.
рис. 3, 4) графическое изображение закона
распределения модуля оценки углового
рассогласования напоминает изображение
эрланговского закона первого порядка. В третьем
случае (см. рис. 5) график ![]() при достаточно высоких (более 100)
отношениях сигнал/шум напоминает кривую
плотности распределения нормального закона.
при достаточно высоких (более 100)
отношениях сигнал/шум напоминает кривую
плотности распределения нормального закона.
Знак ![]() формируется
на основании оценок начальных фаз огибающих
сигналов в суммарном и разностном каналах
приемного тракта
формируется
на основании оценок начальных фаз огибающих
сигналов в суммарном и разностном каналах
приемного тракта
![]() (12)
(12)
где ![]() ;
; ![]() ;
; ![]() – оценки амплитуд и начальных фаз сигналов в
суммарном и разностном каналах приемного тракта;
– оценки амплитуд и начальных фаз сигналов в
суммарном и разностном каналах приемного тракта;
![]() – угловое
рассогласование линии визирования цели (ЛВЦ) и
равносигнального направления (РСН).
– угловое
рассогласование линии визирования цели (ЛВЦ) и
равносигнального направления (РСН).
Выражение, описывающее плотность вероятности начальной фазы огибающей смеси радиосигнала и узкополосного шума, известно [2] и имеет вид
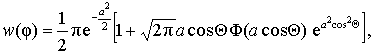 при
при ![]()
где ![]() ;
;
![]() – несущая
частота узкополосного квазигармонического шума
в приемном тракте;
– несущая
частота узкополосного квазигармонического шума
в приемном тракте;
![]() – начальная
фаза полезного сигнала в приемном тракте;
– начальная
фаза полезного сигнала в приемном тракте;
![]() – интеграл
вероятности.
– интеграл
вероятности.
Для упрощения математических
преобразований и с учетом узкополосности
квазигармонического шума предположим равенство
несущих частот сигнала и шума ![]() . В нашем случае начальная фаза сигнала
. В нашем случае начальная фаза сигнала ![]() в соответствующем канале
приемного тракта представляет собой сумму
начальной фазы эхосигнала и значения фазовой ДНА
МИ–антенны.
в соответствующем канале
приемного тракта представляет собой сумму
начальной фазы эхосигнала и значения фазовой ДНА
МИ–антенны.
Тогда выражения для плотностей распределения начальных фаз огибающих смеси сигнала и белого шума в соответствующем канале приемного тракта имеют вид
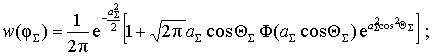
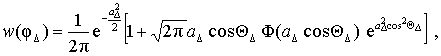
где ![]() ;
; ![]() .
.
Предположим, что ![]() , тогда
, тогда ![]() .
.
Для малых и больших отношений
сигнал/шум выражения, описывающие ![]() и
и ![]() ,
упрощаются [2]. При
,
упрощаются [2]. При ![]() ,
, ![]() формулы, описывающие
формулы, описывающие ![]() и
и ![]() ,
имеют вид
,
имеют вид
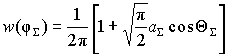 ; (13)
; (13)
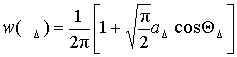 . (14)
. (14)
При ![]() ,
, ![]() формулы, выражающие
формулы, выражающие ![]() и
и ![]() ,
принимают вид
,
принимают вид
![]() ; (15)
; (15)
![]() . (16)
. (16)
Найдем плотности вероятностей
разности случайных фаз ![]()
![]() для разных отношений
сигнал/шум в каналах приемного тракта. Случайные
величины
для разных отношений
сигнал/шум в каналах приемного тракта. Случайные
величины ![]() ,
, ![]() , как и в случае с амплитудами, будем
считать независимыми. Воспользуемся известным
выражением для плотности вероятности разности
двух независимых случайных величин [5]:
, как и в случае с амплитудами, будем
считать независимыми. Воспользуемся известным
выражением для плотности вероятности разности
двух независимых случайных величин [5]:
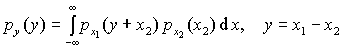 . (17)
. (17)
Для первого случая отношения сигнал/шум в каналах приемного тракта плотность распределения вероятности разности начальных фаз огибающих сигналов в суммарном и разностном каналах описывается выражением, полученным с учетом формул (13), (14), (17):
![]() . (18)
. (18)
Для второго случая плотность вероятности разности начальных фаз огибающих сигналов в суммарном и разностном каналах описывается выражением, полученным с учетом формул (14), (16), (17):
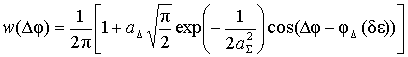 . (19)
. (19)
Для третьего случая плотность распределения вероятности разности начальных фаз огибающих сигналов в суммарном и разностном каналах описывается выражением, полученным с учетом формул (15), (16), (17):
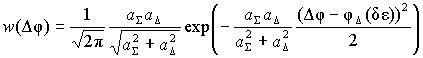 . (20)
. (20)
Согласно формуле (12), знак углового
рассогласования зависит от косинуса разности
фаз, поэтому для нахождения плотности
вероятности знака ![]() перейдем в выражениях (18–20) от разности
огибающих к их косинусу. Для этого воспользуемся
известным выражением для плотности вероятности
функции одного случайного аргумента [6]:
перейдем в выражениях (18–20) от разности
огибающих к их косинусу. Для этого воспользуемся
известным выражением для плотности вероятности
функции одного случайного аргумента [6]:
![]()
где ![]() –
функция, обратная исходной функции случайного
аргумента.
–
функция, обратная исходной функции случайного
аргумента.
В нашем случае обратная функция
случайного аргумента (введем обозначение ![]() ) имеет вид
) имеет вид
![]() (21)
(21)
Функция (21) при ![]() является двухзначной, т. е. имеет две
ветви:
является двухзначной, т. е. имеет две
ветви: ![]() и
и ![]() , поэтому для нахождения плотности
распределения вероятности знака
, поэтому для нахождения плотности
распределения вероятности знака ![]() необходимо воспользоваться
следующей формулой:
необходимо воспользоваться
следующей формулой:
![]() . (22)
. (22)
Производная функции (21) равна
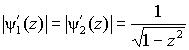 .
.
Для первого случая отношения сигнал/шум в каналах приемного тракта плотность распределения вероятности знака углового рассогласования получена с учетом формул (18) и (22):
![]() . (23)
. (23)
Для второго случая плотность вероятности знака углового рассогласования получена с учетом формул (19) и (22)
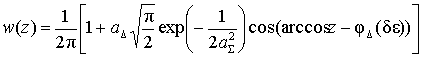 . (24)
. (24)
Для третьего случая плотность вероятности знака углового рассогласования получена с учетом формул (20) и (22)
![]()
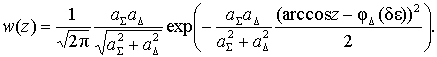 (25)
(25)
Графики, построенные по выражениям
(23–25), показаны соответственно на рис. 6–8 (для
истинного значения ![]() ).
При нулевом отношении сигнал/шум в разностном
канале приемного тракта этот закон, согласно
выражениям (18, 19), трансформируется в закон
равномерной плотности. А из анализа выражения (20)
следует, что в третьем случае распределение
разности фаз является нормальным.
).
При нулевом отношении сигнал/шум в разностном
канале приемного тракта этот закон, согласно
выражениям (18, 19), трансформируется в закон
равномерной плотности. А из анализа выражения (20)
следует, что в третьем случае распределение
разности фаз является нормальным.
Из анализа графиков (рис. 6, 7) следует, что в первых двух случаях имеет место большая вероятность появления ошибочных решений (положительного знака углового рассогласования). При близком к нулевому отношению сигнал/шум эта вероятность равна 0,5. А из графиков (рис. 8) следует, что эта вероятность достаточно мала и при отношениях сигнал/шум в двух каналах приемного тракта, больших пяти, можно говорить о безошибочном нахождении знака углового рассогласования анализируемым измерителем.
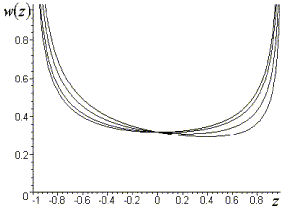
Рис. 6.
Графики зависимостей плотности вероятностей знака для 1-го случая
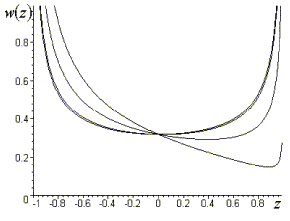
Рис. 7.
Графики зависимостей плотности вероятностей знака для 2-го случая
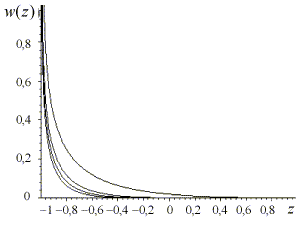
Рис. 8.
Графики зависимостей плотности вероятностей знака для 3-го случая
Анализ выражений для плотностей вероятностей модуля и знака углового рассогласования доказывает, что данные плотности вероятностей нормализируются только при очень больших отношениях сигнал/шум как в суммарном, так и в разностном каналах приемного тракта. Таким образом, применение амплитудного моноимпульсного метода измерения угловых координат цели с суммарно–разностной обработкой сигналов в обзорной РЛС требует специальных мер для увеличения отношения сигнал/шум, в частности, можно использовать результаты накопления пачки эхосигналов, получаемой после обзора пространства.
Литература
FINDING of DENSITY of PROBABILITY of an ESTIMATION ANGULAR MISALIGNMENTS FOR OVERVIEW AMPLITUDE TOTAL – INCREMENTAL MONOPULSE SYSTEM
S. A. Vashkevich
As a result of statistical test overview amplitude total–incremental monopulse system are received analytical expressions, describing density of probability of the evaluation a modula and sign of the angular unbalance between interchangeably signal by the direction and direction on the object for three distinctive events a relations a signal–noise in receiving channels of the system: small relations in total and incremental; the greater – in total, small – in incremental; the greater – in total and incremental. Carry out a test has allowed to reveal a main defect of the given meter.
Кафедра радиоэлектроники
Военный университет войсковой ПВО ВС РФ
Поступила в редакцию 19.04.2003.