Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 8. -
Вып. 3. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/TITL-23.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/cont.htm
УДК 623.658.58
ВЫБОР МОДЕЛИ ПРОЦЕССА
ЭКСПЛУАТАЦИИ РЭС ВООРУЖЕНИЯ ВОЙСКОВОЙ ПВО
Ó 2009 г. Утенков Ю. О.
В данной
работе рассмотрена модель системы процесса эксплуатации РЭС вооружения совместно
с усовершенствованной полумарковской моделью процесса эксплуатации позволяющая
исследовать влияние количества элементов, закладываемых в ЗИП, а также других
факторов на эффективность функционирования образца вооружения в целом.
Ключевые
слова: эксплуатация РЭС.
Работоспособность комплектующих изделий РЭС вооружения в значительной степени зависит от их сложности, функционального назначения, условий применения, особенностей конструктивных решений, характера протекающих рабочих процессов и стабильности технических характеристик.
Оценка коэффициента готовности комплектующих изделий по имеющимся структурно-функциональным и справочным данным по l - характеристикам на элементную базу не представляет особого труда. Однако достоверность такого расчета относительно низкая, поскольку справочные данные по l - характеристикам элементной базы получены в условиях, существенно отличающихся от режимов их работы в войсках. Кроме того, расчеты такого рода, как правило, не учитывают условий эксплуатации и способов (методов) контроля.
Разработка предложений по обеспечению запасными элементами РЭС вооружения предполагает подготовку целого ряда исходных данных. К ним относятся сведения о составе РЭС вооружения, безотказности и среднем времени восстановления его элементов, значениях ошибок I и II родов, характеризующих достоверность контроля и др. Эти данные позволят выбрать или разработать модель процесса эксплуатации, исследование которой позволит разработать методику обоснования РЭС вооружения запасными элементами.
Наиболее перспективным направлением моделирования процесса эксплуатации РЭС вооружения, является использование теории полумарковских процессов.
Основываясь на указанных выше сведениях и учитывая
специфику процесса эксплуатации вооружения, рассмотрим зависимость
вероятностных характеристик РЭС от основных параметров процесса эксплуатации.
Допустим, что техническое обслуживание радиоэлектронных средств образца
вооружения сводится к контролю одного обобщенного параметра, нахождение
которого в допусковой области соответствует его работоспособному состоянию, а
вне ее – отказовому. Этот параметр периодически проверяется, и по результатам
его контроля судят о техническом состоянии всех РЭС вооружения. Это допущение
справедливо также в случае, когда проводится проверка технического состояния
РЭС вооружения на конечном множестве технических параметров, т. е. указанный
выше обобщенный параметр является векторным. Периодичность контроля РЭС
вооружения определяется как продолжительность межрегламентного промежутка ТОБ,
по истечении которого РЭС вооружения
проверяется в течение случайного времени tк,
ограниченного сверху временем ТК, т. е. tк £
ТК. Более строгой оценкой длительности контроля, вообще говоря,
является верхняя граница одностороннего доверительного интервала, вычисленная с
заданной выбранной доверительной вероятностью g:
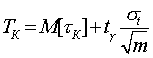(1.1)
где М[tк] – оценка среднего значения продолжительности контроля, полученная по результатам m опытов,
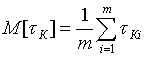
τКi – длительность контроля в i-м эксперименте,
t
– оценка среднеквадратического отклонения случайной продолжительности контроля,
полученная после обработки результатов m опытов, и определяемая
по формуле
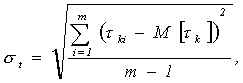
tg - g-процентная квантиль t-распределения Стьюдента с (m-1) степенями свободы.
Обнаружение отказов РЭС вооружения происходит только во время проведения контроля технического состояния (КТС), перед началом которого аппаратура контроля (АК) проходит самоконтроль.
Чем сложнее аппаратура РЭС вооружения, тем более сложной является его АК и тем большее значение приобретает достоверность самоконтроля, особенно такая составляющая как вероятность ошибки второго рода. Поэтому при разработке модели процесса эксплуатации РЭС вооружения необходимо учитывать в первую очередь возможность снижения достоверности контроля в случае пропуска отказа АК при самоконтроле. В силу того, что самоконтроль АК проводится перед началом проверки РЭС вооружения, то показатели надежности и РЭС вооружения, и его АК являются функциями периодичности проверок. С учетом ошибок, возникающих при самоконтроле АК и контроле самих РЭС вооружения в процессе эксплуатации этих средств, могут возникнуть следующие ситуации.
1. Перед проверкой аппаратура объекта контроля (OK) с вероятностью 1-РРЭС(ТОБ.) работоспособна, АК с вероятностью 1-РК(ТОБ.) работоспособна. В результате проведения контроля в этой ситуации могут быть приняты следующие решения:
а) ОК отказал (регистрация ложного отказа или ошибка I рода) – с вероятностью F1. В этом случае проводится расширенный контроль, позволяющий выявить достоверно отсутствие отказа. В частности, "обнаружение" ложного отказа может быть вызвано сбоем АК и расширенный контроль, в случае автоматического встроенного контроля, заключается либо в повторном включении режима проверки, либо, в случае неавтоматического контроля, в использовании других внешних более совершенных средств контроля. Указанный расширенный контроль проводится в течение ограниченного сверху времени tрк £Трк.
б) ОК работоспособен (правильное определение вида технического состояния РЭС вооружения) – с вероятностью 1-F1. B этом случае по окончании контроля, ОК продолжается использоваться по назначению.
2. До проведения контроля ОК с вероятностью 1–РРЭС(ТОБ) работоспособен, АК с вероятностью РК(ТОБ) отказала. В зависимости от исхода контроля, а также характера отказа АК по результатам контроля ОК могут быть произведены следующие оценки его состояния:
а) ОК отказал (ложный отказ) – с вероятностью F2. В этой ситуации проводится описанный выше расширенный контроль;
б) ОК работоспособен - с вероятностью 1-F2.
3. До начала контроля аппаратура ОК с вероятностью РРЭС(ТОБ) отказала, АК с вероятностью 1 – РК(ТОБ) работоспособна. По результатам контроля могут быть приняты следующие решения:
а) ОК отказал (обнаружение отказа) – с вероятностью D1. В этом случае на ОК проводится расширенный контроль с целью подтверждения наличия отказа и его локализации, а затем восстановление ОК в течение общего времени tв < Тв;
б) ОК работоспособен (пропуск отказа) – с вероятностью 1 – D1. В этом случае РЭС вооружения продолжает эксплуатироваться со скрытым отказом, снижающим эффективность применения ОК по назначению в лучшем случае, до следующей проверки. Подобные случаи характерны для РЭС вооружения имеющих несколько видов контроля, отличающихся, прежде всего, по полноте охвата контролем подсистем и функциональных узлов.
4. К началу проведения контроля ОК с вероятностью РРЭС(ТОБ) отказал, АК с вероятностью РК(ТОБ) отказала. В зависимости от результатов самоконтроля и характера отказа АК производится следующая оценка состояния РЭС вооружения:
а) ОК отказал – с вероятностью D2 и проводится расширенный контроль с последующим восстановлением;
б) ОК
работоспособен (пропуск отказа) – с вероятностью 1 – D2, что приводит к ситуации,
описанной в пункте 3б.
Наиболее содержательные модели описанного процесса эксплуатации РЭС были получены с помощью математического аппарата теории полумарковских процессов (ПМП) профессорами Сычёвым Е.И. [1] и Мищенко В.И. [2]. В качестве методики задания ПМП использовался традиционный подход, описанный, например, в работе [3]. Суть его, интерпретированная к решению научной задачи, сводится к следующему.
Пусть Е = {1,2,…,r} множество возможных состояний, в которых может находиться ОК, тогда
xij - случайная продолжительность пребывания ПМП в состоянии i при условии перехода в состояние j на очередном интервале контроля;
Fij(t) = P(0 £ xij < t) - функция распределения случайной величины xij, tÎ[0, ТОБ ].
Исчерпывающее
описание эволюции ПMП
на множестве возможных состояний при известном начальном состоянии задается
стохастической матрицей W={ wij
}, i,jÎE
вероятностей переходов вложенной в ПМП Марковской цепи и матрицей условных
функций распределения F(t)= ( Fij (t)}, i,jÎE.
Далее, в соответствии с традиционными формулами
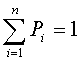(1.2)
где n – число состояний ПМП;
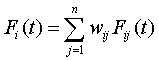, (1.3)
где Fi(t) – безусловные функции
распределения продолжительности пребывания в состоянии i, 
до ухода в любое
состояние j,
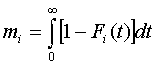, (1.4)
где mi – математическое ожидание продолжительности пребывания в состоянии i до ухода из него;
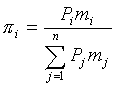(1.5)
(1.2),…,(1.5) отыскивались финальные вероятности состояний ПМП, позволившие рассчитать выбранный показатель эффективности процесса эксплуатации (в частности, приведенный в первом разделе коэффициент готовности РЭС вооружения).
Для модели профессора Сычёва Е.И. множество возможных состояний процесса включало:
Е1 – работоспособное состояние ОК;
Е2 – отказ ОК;
Е3 – проверка отказавшего ОК;
Е4 – ОК восстанавливается;
Е5 – проверка работоспособного ОК;
Е6 – необнаруженный отказ ОК.
Граф изменения состояний представлен на рисунке 1, где
F, D – вероятности обнаружения ложных и действительных отказа в ОК соответственно.
Матрица вероятностей переходов вложенной Марковской цепи W, соответствующая графу состояний, приведенному на рисунке. 2.1, представлена на рисунке 2.
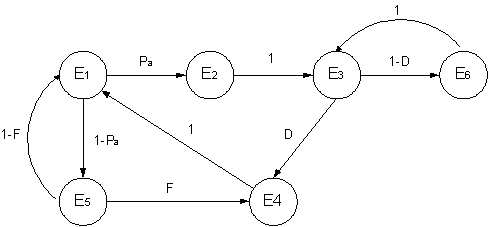
Рис. 1. Граф состояний модели процесса
эксплуатации профессора Е.И. Сычёва
|
|
0 |
Ра |
0 |
0 |
1-Ра |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
W = |
0 |
0 |
0 |
D
|
0 |
1-D |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
1-F |
0 |
0 |
F
|
0 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
Рис. 2. Матрица вероятностей переходов вложенной Марковской цепи
В соответствии с соотношением (1.2) система линейно независимых
уравнений запишется в виде
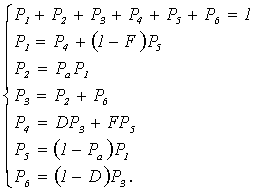
С использованием формулы (1.3–1.4) математические ожидания времени пребывания ОК в состояниях имеют вид
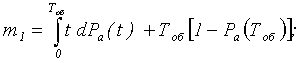
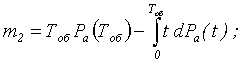
m3 = m5 = Tк ; m4 = TВ ; m6 = Tоб .
В соответствии с
результатами решения системы уравнений и применения формулы (2.5) финальная вероятность
пребывания в первом состоянии, соответствующая коэффициенту готовности РЭС
вооружения примет вид
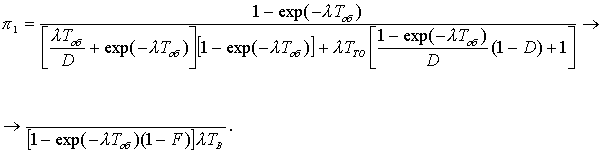
Приведенная
модель учитывает метрологическое обеспечение эксплуатации РЭС вооружения, но не
учитывает безотказность средств измерений, влияющую на достоверность контроля.
Кроме этого в этой модели не учитывается эффективность технического
обслуживания, зависящая от уровня обеспеченности запасными частями, а также
стратегией их пополнения. Существует еще одно ограничение в использовании
данной модели процесса эксплуатации. Оно обусловлено предположением автора об
идентичности восстановления системы после ложной регистрации отказа и
действительного обнаружения отказа системы. В тоже время основным отличием
восстановления работоспособности системы в этих случаях является то, что в
первом случае проводится повторный контроль по отказавшему техническому
параметру, а во втором случае восстанавливается ресурс элемента путем замены
или регулировки его параметров.
Свободной от
приведенных ограничений является модель, предложенная профессором В. И.
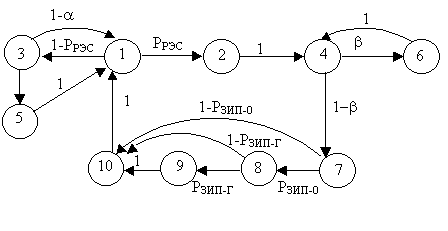
Мищенко. Граф этой модели включает уже десять состояний.
E1 – ОК исправен (исходное состояние ПМП);
E2 – ОК неисправен или отказал, но до проверки этот факт ещё не обнаружен (попутно заметим, что в литературе зачастую и причем необоснованно такой вид отказов, снижающий эффективность функционирования, но не приводящий к полному отказу РЭС вооружения называют «скрытым». В тоже время, если отказ является скрытым, то он не соответствует гостированному понятию отказа);
E3 (E4) – ОК проверяется при условии, что он к началу проведения проверки работоспособен (неисправен или отказал);
E5 – ОК проходит расширенный контроль в случае ложной регистрации отказа;
E6 – ОК функционирует с неисправностью до очередной проверки (при имеющейся заданной полноте контроля данный отказ РЭС не обнаруживается, самостоятельно не проявляется, но приводит к снижению эффективности функционирования образца);
E7 – ОК диагностируется на предмет локализации выявленного отказа и отыскивается требуемый элемент в ЗИП-О;
Е8 – ОК ожидает удовлетворения заявки на постановку элемента, взамен отказавшего, из ЗИП-Г;
Е9 – ОК ожидает экстренной доставки элемента, отсутствующего и в ЗИП-О, и в ЗИП-Г;
Е10 – ОК восстанавливается (производится замена отказавшего элемента).
Размеченный граф процесса, матрица W представлены на
рисунке 3. В матрице W
(1.6)
где
РРЭС(TОБ) – вероятность
возникновения отказа в аппаратуре ОК на интервале [0, TОБ];
РК(TОБ) – вероятность возникновения отказа в
аппаратуре контроля на этом же
интервале;
D – вероятность обнаружения отказа в ОК;
F – вероятность ложной регистрации отказа в
ОК;
λРЭС, λК – интенсивности отказов аппаратуры ОК и АК
соответственно.
Перейдем к получению элементов матрицы F(t). Введем:
tотк – случайный момент времени возникновения
отказа в ОК, причём 0 < tотк < TОБ;
tотк = TОБ – tотк – случайная
продолжительность существования неисправности (отказа) от момента её (его)
возникновения до начала проверки (0<tотк<TОБ);
ТК – верхняя
граница продолжительности проверки, рассчитываемая по формуле (1.1);
ТРК – верхняя
граница продолжительности расширенного контроля, рассчитываемая по формуле
(1.1);случайная продолжительность расширенного контроля.
0
|
PРЭС |
1-PРЭС |
0
|
0
|
0
|
0
|
0
|
0
|
0
|
||
0
|
0
|
0
|
1 |
0
|
0
|
0
|
0
|
0
|
0
|
||
|
1-a |
0
|
0
|
0
|
a |
0
|
0
|
0
|
0
|
0
|
||
|
0 |
0
|
0
|
0 |
0
|
b
|
1-b
|
0
|
0
|
0
|
||
|
W = |
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
||
0
|
0
|
0
|
1 |
0
|
0
|
0
|
0
|
0
|
0
|
||
0
|
0
|
0
|
0
|
0
|
0
|
0
|
РЗО |
0
|
1-РЗГ
|
||
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
РЗГ
|
1-РЗГ
|
||
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1 |
||
|
1 |
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
а)
a
б)
Рис.
3.Модель процесса эксплуатации: матрица переходов вложенной Марковской цепи (а), размеченный граф полумарковского
процесса, описывающего взаимодействие РЭС вооружения с системой его эксплуатации
(б)
ТЗАМ – среднее время замены, отказавшего элемента;
ТД – среднее время диагностирования с целью локализации отказов;
ТЗИП – среднее время простоя ОК из-за отсутствия требуемого элемента в одиночном комплекте ЗИП и необходимости обращения к групповому комплекту ЗИП;
ТЭД – среднее время экстренной доставки требуемого элемента в случае отсутствия такового в групповом комплекте ЗИП.
Тогда с учетом специфики функционирования РЭС вооружения ненулевые компоненты матрицы F(t) примут вид
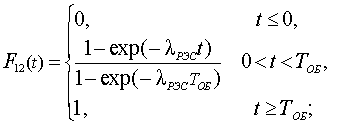
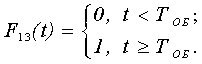
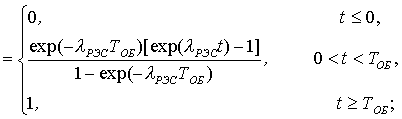(1.7)
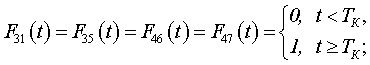
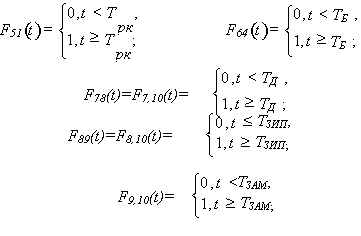
Далее, в соответствии с (1.2), определим составляющие вектора-строки P = (Р1, Р2,…, Рr), который является собственным вектором матрицы W, удовлетворяющим к условию нормировки. В рассматриваемом случае соотношения (1.2) приводят к системе линейно независимых алгебраических уравнений
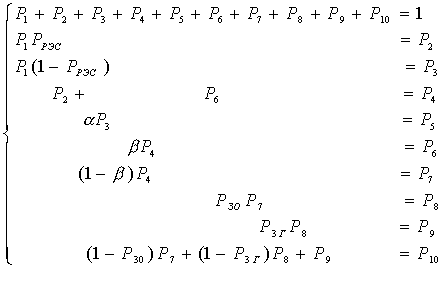(1.8)
Решением системы уравнений (1.6) является набор (Р1, Р2,…, Р10)
; 
; 
; 
; 
;
; 
; 
; 
; 
Рассчитаем теперь величины mj, используя соотношения (1.2) – (1.4).
Таким образом,
.
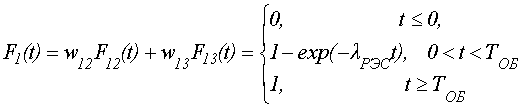
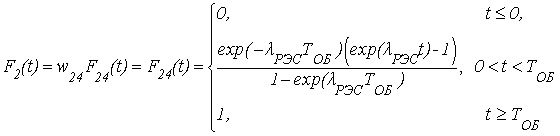Тогда
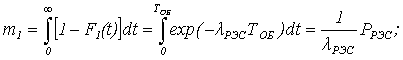
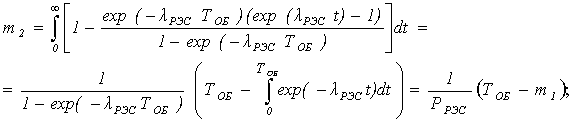
m3 = m4 = TК; m5 = TРК; m6 = TОБ; m7 = TД; m8 =
ТЗИП; m9 = ТЭД;
m10 = ТЗАМ.
С учетом полученных соотношений найдем выражения для финальных вероятностей pi по формуле (1.5). После соответствующих преобразований получим
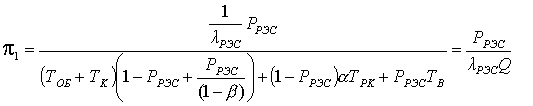, (1.9)
где ТВ = ТЗАМ + ТД + Р3О(ТЗИП + Р3ГТЭД);
.
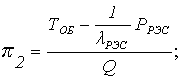
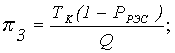
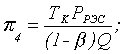
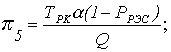
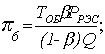
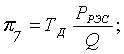
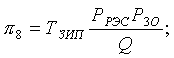
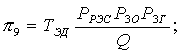
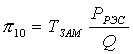Здесь p1 - вероятность застать ОК работоспособным и не находящимся на обслуживании в любой произвольный момент времени. Вероятность p1 соответствует введенному выше коэффициенту готовности РЭС КГ и является функцией основных параметров системы эксплуатации, а именно:
периодичности обслуживания – ТОБ;
продолжительности обслуживания – ТК;
достоверности проверок, т. е. ошибок первого и второго родов (a и b), зависящих от полноты контроля, точности измерений и безотказности аппаратуры контроля;
продолжительности расширенного контроля, обусловленного ошибкой первого рода («ложными» отказами) – ТРК;
продолжительности восстановления – ТВ = ТЗАМ + ТД + Р3О(ТЗИП + Р3ГТЭД), зависящей от конструктивных особенностей РЭС ТЗАМ, эффективности средств локализации отказов и уровня квалификации ремонтного персонала ТД, а также, что является в нашей ситуации наиболее весомым, качества проектирования и организации пополнения комплектов запасных элементов Р3О, Р3Г, ТЭД;
уровня безотказности РЭС вооружения, зависящего от условий и интенсивности эксплуатации, квалификации эксплуатирующего персонала – РРЭС или lРЭС;
продолжительности диагностирования (локализации отказов) – ТД, зависящей от уровня автоматизации контроля параметров РЭС и определяющей, в свою очередь, требуемый уровень квалификации обслуживающего персонала;
продолжительности замены отказавшего элемента – ТЗАМ, зависящей от конструкции РЭС вооружения;
времени задержки – ТЗИП, зависящего от распределения запасных элементов между комплектами и правильности проектирования ЗИП;
времени экстренной доставки – ТЭД, зависящего от вышеназванных последних факторов и удаленности РЭС вооружения от завода изготовителя или арсеналов.
При этом в качестве показателя достаточности комплектов ЗИП, как видно из приведенных выше формул выступает коэффициент готовности образца вооружения, зависящий от периодичности и объема ТО, номенклатуры и состава комплектов ЗИП и других эксплуатационных факторов.
Литература
1. Сычев Е.И.
Метрологическое обеспечение радиоэлектронной аппаратуры. М.: РИЦ
"Татьянин день", 1993. - 277с.
2. Мищенко В.И. Модели процесса эксплуатации. Сборник
трудов АВН, 2002, с. 75-81.
3. Мищенко В. И. Пути повышения надежности радиоэлектронных
средств ЗРК//Научные труды университета. Вып. 2. Смоленск, ВУ ВПВО ВС РФ, 1999.
С. 156-165.
CHOICE TO MODELS OF THE PROCESS TO USAGES RES
ARMSES V PVO
Utenkov
Y. O.
In given work is considered system model of the process to usages RES armses
with advanced polumarkovskoy by model of the process to usages allowing
research the influence an amount element, pawned in ZIP, as well as the other
factor on efficiency of the operation sample armses as a whole.
Key words: process to usages RES.
Академия
войсковой ПВО Вооруженных Сил РФ
им.
Маршала Советского Союза А. М. Василевского, г. Смоленск
Поступила в редакцию 19.09.2009.