Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 1. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/TITL-25.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/cont.htm

 

УДК 517.927

 

Приближенный метод решения сингулярной задачи Николетти

 

© 2010 г. Исраилов С. В., Сагитов  А. А.

 

(israilov-3.doc)

 

В статье путем использования экстремальных дифференциальных неравенств обосновывается приближенный метод решения многоточечной сингулярной краевой задачи Николетти для системы обыкновенных дифференциальных уравнений. Устанавливаются оценки быстрого сходимости итерационного процесса.

Ключевые слова: сингулярность, неравенства, приближения, сходимость, оценка.

 

Система дифференциальных уравнений

                                                                                 (1)

с условиями задачи Коши

                      ,                                                                            (2)

когда функции ,  , непрерывны по совокупности аргументов в области , а при имеют сингулярность неинтегрируемого характера  подробно исследованные в работе  с приведением и приближенного метода нахождения непрерывного решения задачи (1), (2).

Когда каждая правая часть  при фиксированном  имеет свою точку сингулярности , но в области  непрерывна или удовлетворяет условиям Каратеодори, для системы (1) ставилась задача Николетти  с условиями

                                                                  

                      ,                                                                 (3)

 

и доказывались различные теоремы существования и единственности решения задачи (1), (3), но нигде не обоснован приближенный метод решения этой сингулярной задачи.

         Здесь, ссылаясь на простую теорему существования и единственности решения, сделана попытка одолеть указанный пробел.

         Теорема 1. Пусть в области  существуют производные  , причем

 

                      ,   ,                                 (4)

 

                      ,   ,                                          (5)

                                               

                 ,   ,  ,                                    (6)

где - непрерывная суммируемая функция на .

       Тогда задача (1), (3) имеет единственное непрерывное решение , .

Существование решения доказано в работе . Для доказательства единственности применяется теорема

 

          Теорема 2. Пусть функции , , удовлетворяют системе (1) и условиям (3) при  и справедливы неравенства

 

                 

                           ,                                                    (7)

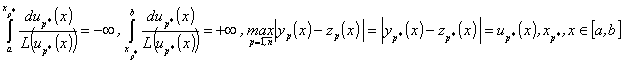где  ,     (8)

Тогда задача (1), (3) имеет не более одного решения, т.е. ,

Доказательство теоремы 2 несложно, если учесть условия (5), (6) и (7), (8). В условиях теоремы 1  и (8) выполнены.

        

         2. Предлагаемый приближенный метод решения задач (1), (3) основан на известной идее С. А. Чаплыгина , развитой в работе .

         В качестве «верхних» и «нижних» нулевых приближений выбираются функции

 

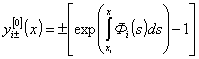                       ,  ,                                       (9)

где                 ,                                 (10)

в предположении, что             

                         ,  .                                                (11)

Введем область:

                      .                                  (12)

Лемма 1.  Нулевые приближения  в  удовлетворяют неравенствам:

                                    .                                                           (13)      При

                     ,                 (14)      

            .                           (15)

При

                ,                     (16)

               .                         (17)

 

В силу (10) доказательство (13) очевидно. Докажем неравенства (14), (15)  при , . Из (9) и (10) имеем                

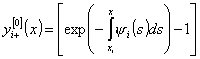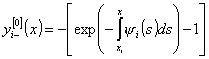        , .                       (18)

Продифференцируем выражения (18) по :

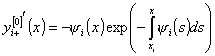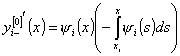             ,  .                     (19)

С учетом (18) из (19) получим

             , .                                 (20)

Из-за непрерывности функции  по  в замкнутой области   на  существуют такие измеримые вектор-функции , что

       .    (21)

 

      .     (22)

Следовательно, с учетом (20) – (21) из (14), (15) имеем

     .            (23)

     .              (24)

Так как существуют частные производные , выражения (23), (24) можно записать так:                  

  ,    (25)

  .        (26)

Отсюда, если иметь в виду условия (4), (5) и равенства (9), (10), справедливы неравенства

  ,      ,                                                                    (27)

 

что и требовалось доказать. При  неравенства  (16), (17) доказываются аналогично. 

Обозначим

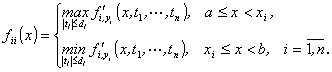                                               (28)

Эти функции определены и непрерывны на , . На участках  первые «верхние» и «нижние»  функции введем равенствами

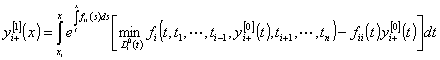      ,   ,    (29)

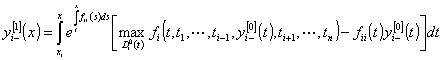      ,   ,    (30)

а на участках   равенствами

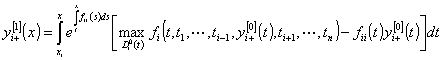      ,   ,    (31)   

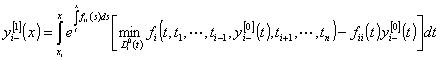      ,   .     (32)

Надо доказать, что внешние интегралы в правых частях (29) - (32) сходятся. Возьмем правую часть равенства (29) (обозначим ее через ) и преобразуем ее методом получения (25), (26) из (21), (24): 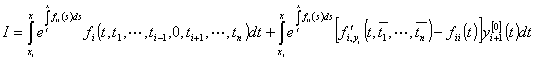,   . (33)

Первый интеграл в правой части (33) сходится в силу (4), (5). Второе слагаемое  можно представить в виде

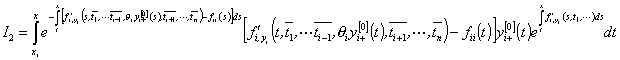.       (34)

Отсюда

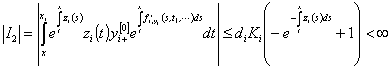                ,                 (35)  

 

где (см. (28)

               ,    ,             (36)                             

,   .

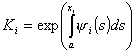Аналогично доказывается ограниченность интегралов в правых частях (30)-(32).

Построим область .

Теперь покажем что функции (29)-(32) удовлетворяют условиям    

                 .                                              (37)

     ,   ,           (38)

    ,   ,               (39)

    ,   ,               (40)         

   ,  ,                 (41)                             

                                                  , .                                          (42)

Положим при

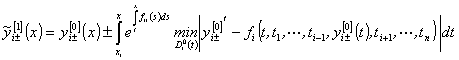           .         (43)

Неравенства (14), (15)позволяют представить (43) в другой форме 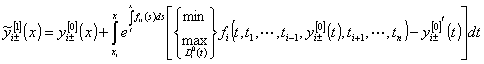  ,   .   (44)

 

Интегрируя по частям, преобразуем интеграл

                                  ,         

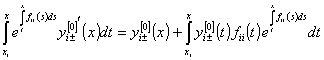и подставляя в правую часть (44), получим правые части равенств (29), (30), т.е. 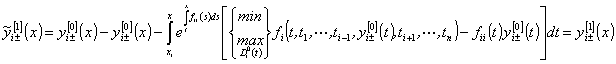 ,  .                                                                                                             (45)

Сравнивая (43) и (45), получим

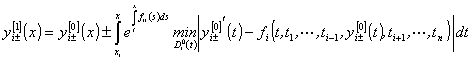      .              (46)

Так как в (46) , то ясно, что  и . Остается доказать . Обе части (46) продифференцируем по :

              

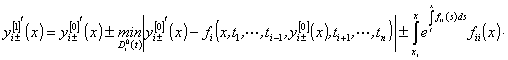
                  .                                       (47)

Воспользовавшись (47), из равенств для   вычтем равенства для  и с учетом снова (46) получим    

                ,   ,                           (48)

где

                           

 

 

 

 

     

 

                                 ,                                           (49)

 

из-за (9), (28) и определения экстремумов. Проинтегрируем (48) с учетом условий , знака  при  в (49):

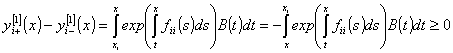          ,            (50)

т.е.  ,   ,  .  Аналогично доказываются неравенства (37) и при . Докажем теперь (38)-(41). Обозначим через,  ,  , такие функции, что (см. (38) (39))

              ,  .                       (51)

Из (46) вытекает, что

                                     

 

              

         

   .            (52)

Учитывая (14), (15), (28) и (37), приходим к неравенствам (38) и (39) при . Для  аналогично доказываются неравенства (40) и (41). Выполнение (42) следует из (46) при .

Доказано, что функции  из(29)-(32) обладают такими же свойствами, что и функции  из (9). Это позволяет построить функции  и т.д.

Если построена уже -я система функций , , то -я система функций или -е приближение к решению определяется равенствами

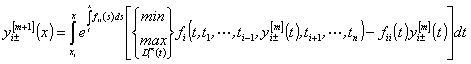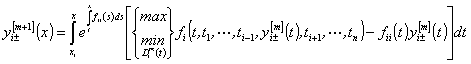,  ,    (53)   ,   , ,                                                                                                                (54)

 

где . Точно также показывается, что функции  непрерывно дифференцируемы на ,  и удовлетворяют условиям:

               ,  , ,                            (55)

         , , ,           (56)

         ,  , ,            (57)

 

       ,  , ,             (58)

        , ,              (59)

                                  ,.                                           (60)

 

3. Теорема 3. В условиях теоремы 1 последовательности функций (53), (54) равномерно и монотонно сходятся к решению задачи (1), (3).

         Действительно, монотонность последовательностей (53), (54) вытекает из (55), как и точечная сходимость. Условия теоремы достаточны, чтобы доказать их компактность (равномерную ограниченность и равностепенную непрерывность) в пространстве  непрерывных вектор-функций, так, что эти последовательности равномерно сходятся .

Обозначим

                      , , ,         (61)

Положим 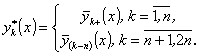                                                           (62)

Покажем, что функции , , из (62) удовлетворяют следующей системе дифференциальных уравнений

             , , ,                    (63)                                    

         ,  , ,            (64)        

       , , ,                          (65)       , , .                      (66)

 

Ограничения из  теоремы 1 в отношении функций , позволяют в (53) и (54) переходить к пределу при , получаются равенства 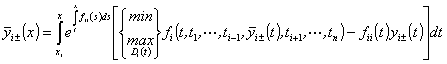 ,  ,        (67)

 

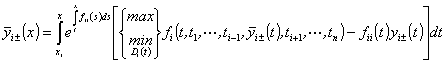    ,  ,    (68)

где .

         Интегралы в (67), (68) являются дифференцируемыми функциями в силу тех же свойств функций , , , поэтому функции  из (67), (68) имеют производные ,что дает возможность проинтегрировать следующие интегралы по частям

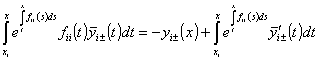                    ,  .                    (69)

Подставив выражения (69) в правые части (67), (68), имеем

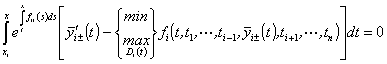       , ,               (70)

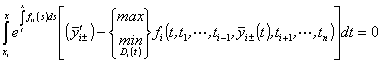     , .                  (71)

Продифференцировав (70), (71) по , приходим к сказанному:

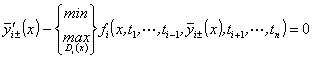             ,  ,                        (72)                                                                 

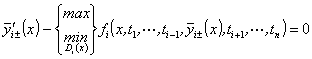            ,  .                        (73)

 

Теорема 4. Система функций , , где - решение задачи (1), (3), удовлетворяет системе дифференциальных уравнений (63)-(66).

         Действительно, пусть . Тогда

 , ,                (74)    , ,                 (75)

и при  из (74), (75) имеем , что противоречит неравенствам (56), (57), поэтому . Точно так же и при :

    ,  ,      (76)

    ,  .            (77)

Если в (76) и (77) положить , имеем , что противоречит неравенствам (58), (59). Теорема доказана, т.е. .

         Остается доказать, что для систем (63)-(66) справедлива теорема единственности решения. Для этого понадобится

          Лемма 2. Пусть , , , непрерывна по совокупности переменных и пусть , . Тогда имеет место неравенство

 

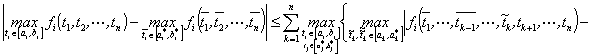
.                                          (78)

 

С учетом условий теоремы 1 в сочетании с  Леммой 2 (неравенством (78)) к системе (63)-(69) применим теорему 2 в отношении двух разных решений  задачи (63)-(66)-(3). Получим неравенство

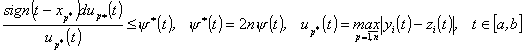,    (79)

где  та из точек сингулярности , , индекс которой совпадает с числом . При    из (79) на интервале  имеем (с учетом )                      

,

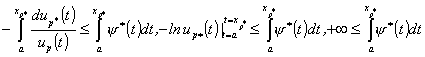чего быть не может. При  из (79) получим

,

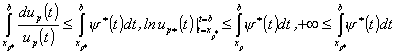что противоречит суммируемости функции . Поэтому  .

Теорема 3 доказана и обоснован метод приближенного решения сингулярной задачи Николетти (1), (3).

         4. Предлагаемый метод можно упростить в различных направлениях. Сложность его заключается в необходимости нахождения экстремумов функций по усложняющимся областям после каждого шага. Если предположить, что каждая частная производная , , не принимает значений разных знаков, то экстремумы будут достигаться на концах интервалов, определяющих область ,   Тогда в формулах (53), (54) будут отсутствовать символы экстремумов.

         Можно установить оценки, характеризующие быстроту сходимости. Например, справедлива.

Теорема 5. Пусть выполнены условия теоремы1и существуют такие непрерывные на  функции , что в области  выполняются неравенства    

                    ,  ,  ,

где  - суммируема, а - либо суммируема, либо не суммируема и  при , . Тогда при достаточно малой длине интеграла справедливы оценки

,

где ,

.

 

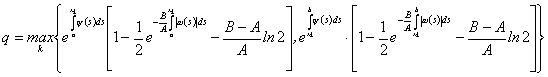Литература

 

1.      Чечик В. А. Исследование систем обыкновенных дифференциальных уравнений с сингулярностью. Труды Московского математического общества, том 8, с. 155-198, 1959.

2.      Исраилов С. В. О сингулярной многоточечной краевой задаче. Ученые записки  Азерб. гос. ун-та. Серия физ-мат. наук, 1963, №3; с. 63-71.

3.      Кигурадзе И.Т. Некоторые сингулярные краевые задачи для обыкновенных дифференциальных уравнений. Тбилиси: Изд-во Тбилисского ун-та, 1975. с. 352.

4.      Чаплыгин С. А. Приближенное интегрирование систем двух дифференциальных уравнений. Собр. Соч., т.1 М, Гостехиздат, 1948, 427-444.  

 

 

 

An approximate method of decision singular Nickoletti's solutions

 

Israilov S. V., Sagitov A. A.

 

In this article by the way of using extreme differential inequalities is based on an approximate method of decision multipointed singular value Nickoletti's solution for the system of ordinary differential equations. The ratings of ratio of integration progress are set.

Keywords: singularity, inequality, approach, ratio, rating.

 

Домашний адрес:

366701, Чеченская Республика, Сунженский район, станица Серноводская, улица Наги Асуева №79, Сагитов Адам Аюпович. E-mail: segitov@mail.ru Тел. моб. 8 928 736 0669

 

364000,  г. Грозный, поселок Калинина, улица Дарвина № 67, Исраилов Сейдахмед Вахидович. Тел. моб. 8 928 476 6402.

Исраилов Сейдахмед Вахидович, профессор кафедры «Алгебра и геометрия», Чеченского государственного университета.

 

Homeaddress:  Chechen Republic.

Naggi Asueva Street, 79

Sernjvodskaya District

Sungenski Region

366 701

 e-mail: segitov@mail.ru

 

 Darvin Street, 67

 Kalinina Settlement

 Grozny / 364 000 / Israilov Seidakhmed Vakhaevich

 

 Israilov Seidakhmed Vakhaevich, professor of "Algebra and Geometry Department" of the Chechen State University

 

Чеченский государственный университет

г. Грозный

Поступила в редакцию 23.03.2010.