Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 9. -
Вып. 2. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm
УДК
517
Линейные
функционалы и операторы в пространстве степенных рядов с быстро убывающими
коэффициентами
Ó
2010 г. Мануилов Н.Ф.
Статья посвящена исследованию линейных отображений пространств
целых аналитических функций многих комплексных переменных, задаваемых
степенными рядами с быстро убывающими коэффициентами. Определена топология, в
которой такие пространства является пространствами и типа Фреше. Найден общий вид линейного функционала в пространстве
указанного типа, дано описание линейных отображений из одного пространства в
другое и базисов в таких пространствах.
Ключевые слова: аналитическая функция, степенный ряд с быстроубывающими
коэффициентами, линейный функционал, линейный оператор, пространство типа
Фреше, базис в линейном пространстве.
В работе исследуются
линейные отображения пространств, обозначаемых далее через ![]() (k ≥ 2) , целых аналитических функций k
комплексных переменных, задаваемых степенными рядами с быстро убывающими коэффициентами.
Определена топология, в которой
(k ≥ 2) , целых аналитических функций k
комплексных переменных, задаваемых степенными рядами с быстро убывающими коэффициентами.
Определена топология, в которой ![]() является пространством типа Фреше.
является пространством типа Фреше.
Найден общий вид линейного функционала в пространстве ![]() , дано описание линейных отображений из
, дано описание линейных отображений из ![]() в
в ![]() и базисов в таких
пространствах.
и базисов в таких
пространствах.
1. Некоторые сведения из комбинаторики
Лемма 1.1.
Число М всех векторов (m1, m2, … , mk) с целыми неотрицательными координатами, являющихся
решениями уравнения
![]() ,
, ![]() ,
,
где m – целое
неотрицательное число, задается формулой
![]() ,
,
где ![]() - число сочетаний,
- число сочетаний,
![]() .
.
Доказательство. См. [4], стр. 23.
Лемма 1.2. Справедливо тождество
![]() ,
,
где ![]() .
.
Доказательство.
См. [5], стр. 8, № 1.3.
Следствие 1.3. Имеет место тождество
![]() ,
, ![]()
![]() .
.
Доказательство
получается путем вычитания тождества из леммы 1.2 при ![]() из такого же
тождества при
из такого же
тождества при ![]() .
.
2. Об одном порядке на множестве ![]()
Пусть ![]()
![]() . На множестве
. На множестве ![]()
![]() ,
, ![]() зададим бинарное отношение «<» следующим образом (1):
зададим бинарное отношение «<» следующим образом (1):
![]()
тогда и только тогда, когда выполняется
числовое неравенство:
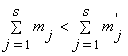
или, при 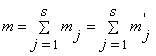 ,
, ![]() , числовое неравенство
, числовое неравенство
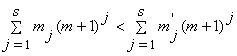 .
.
Лемма 2.1. Отношение «<» на множестве ![]() является отношением строгого линейного порядка.
является отношением строгого линейного порядка.
Доказательство следует из справедливости этого утверждения при ![]() - в этом случае определенное отношение совпадает с отношением
строгого порядка на множестве целых неотрицательных чисел – и единственности
представления целого числа в позиционной системе счисления.
- в этом случае определенное отношение совпадает с отношением
строгого порядка на множестве целых неотрицательных чисел – и единственности
представления целого числа в позиционной системе счисления.
Зададим функцию (2): ![]() по формуле
по формуле
![]()
![]() ,
,
где
n -
номер вектора ![]() в ряду векторов из
в ряду векторов из ![]() , расположенных в порядке (1) (нумерация начинается с
, расположенных в порядке (1) (нумерация начинается с ![]() ).
).
Лемма 2.2. Пусть 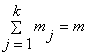 , m>0. Тогда
, m>0. Тогда
![]() ,
, ![]() ,
,
где
l – номер вектора ![]() в последовательности векторов
в последовательности векторов
![]()
![]() ,
,
расположенных
в порядке (1), для каждого из которых выполняется условие: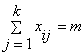 .
.
Доказательство.
Согласно лемме 1.2
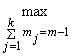
![]() ,
,
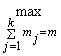
![]() ,
,
По
следствию 1.3
![]() ,
,
что
равно числу элементов множества ![]()
![]()
и
числу векторов ![]() , для каждого из которых выполняется условие
, для каждого из которых выполняется условие
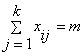 .
.
Из
доказательства леммы 2.2 вытекает
Следствие 2.3.
Отображение (2) ![]() изотонно и имеет обратное.
изотонно и имеет обратное.
3. Определение пространства ![]()
Рассмотрим степенной ряд
![]()
![]()
![]()
![]() , (3)
, (3)
где
![]() - комплексные числа,
- комплексные числа, ![]() - комплексные
переменные, для которых выполняется условие
- комплексные
переменные, для которых выполняется условие
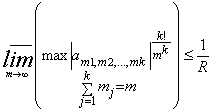 ,
, ![]() . (4)
. (4)
Ряд
(3) при условии (4) определяет целую аналитическую функцию k переменных. Действительно,
![]()
![]()
![]()
![]() ,
,
где ![]() ,
, ![]() .
.
Для
коэффициентов ряда (5):
![]()
выполняется
неравенство
![]()
![]()
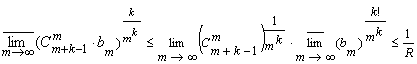 ,
, ![]() ,
,
Следовательно,
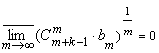
и
ряд (5) сходится при любых значениях переменного х (![]() ), но тогда ряд (3) сходится при любых значениях переменных
), но тогда ряд (3) сходится при любых значениях переменных ![]() .
.
Множество ![]() является линейным пространством с обычными операциями
сложения функций и умножения функции на комплексное число.
является линейным пространством с обычными операциями
сложения функций и умножения функции на комплексное число.
Обозначим через ![]() пространство функций
одного переменного, аналитических в круге
пространство функций
одного переменного, аналитических в круге ![]() . Будем предполагать, что в пространстве
. Будем предполагать, что в пространстве ![]() задана топология,
порожденная нормой (6): для
задана топология,
порожденная нормой (6): для ![]()
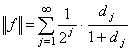 ,
,
где
![]()
![]() , последовательность положительных чисел (
, последовательность положительных чисел (![]() ) монотонно возрастает и
) монотонно возрастает и ![]() . Определим на
. Определим на ![]() оператор Т по
формуле (7): для
оператор Т по
формуле (7): для ![]() ,
,
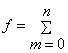
![]()
![]() ,
,
![]()
![]()
![]() ,
,
где
![]() функция (2).
функция (2).
Лемма 3.1. Оператор
(7) устанавливает биекцию линейных пространств ![]() и
и ![]() .
.
Доказательство.
По следствию 2.3 разложение
![]()
![]()
![]()
не
содержит одинаковых степеней ![]() . Кроме того
. Кроме того
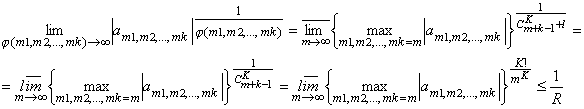
Отсюда
вытекает, что для ![]() . Обратно, любой элемент
. Обратно, любой элемент ![]() , в силу следствия 2.3 единственным образом представим в виде
, в силу следствия 2.3 единственным образом представим в виде
![]()
![]()
![]() ,
,
где
коэффициенты ![]() удовлетворяют условию
(4). Следовательно,
удовлетворяют условию
(4). Следовательно, ![]() , где
, где
![]()
![]()
![]() .
.
Таким
образом оператор Т устанавливает биекцию множеств ![]() и
и ![]() и он, как видно из
определения, линеен. Определим функцию
и он, как видно из
определения, линеен. Определим функцию ![]() как сумму ряда
как сумму ряда
![]()
![]()
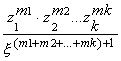 (8)
(8)
Ряд
(8) сходится равномерно и абсолютно на любом множестве вида:
![]() .
.
В
самом деле, на каждом таком множестве
![]()
![]()
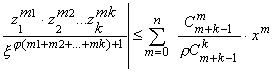 ,
,
где
![]() , а ряд
, а ряд
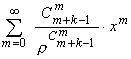
сходится,
так как
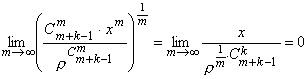 .
.
Лемма 3.2. Любая
функция ![]() из пространства
из пространства ![]() представима в виде:
представима в виде:
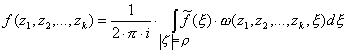 ,
, ![]() (9),
(9),
где
![]() , Т – оператор (7),
, Т – оператор (7), ![]() -
функция (8).
-
функция (8).
Доказательство.
В интеграле
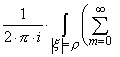
![]()
![]()
![]()
![]()
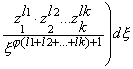 ,
, ![]() ,
,
ряды
сходятся равномерно. Производя перемножение рядов и применяя почленное интегрирование,
получаем (9).
Теорема 3.3.
Пространство ![]() не полно в топологии равномерной сходимости в k -мерном комплексном пространстве
не полно в топологии равномерной сходимости в k -мерном комплексном пространстве ![]() .
.
Доказательство.
Допустим противное. Тогда, в силу (9), оператор Т-1 будет линейным
непрерывным оператором, отображающим пространство АR на пространство ![]() . По известной теореме Банаха, оператор Т также будет
непрерывным, как обратный к Т-1. Фиксируем число R1,
. По известной теореме Банаха, оператор Т также будет
непрерывным, как обратный к Т-1. Фиксируем число R1, ![]() , и пусть последовательность
, и пусть последовательность ![]() элементов пространства АR – некоторая последовательность, сходящаяся равномерно
внутри круга
элементов пространства АR – некоторая последовательность, сходящаяся равномерно
внутри круга ![]()
и
расходящаяся вне этого круга. Предельную функцию этой последовательности обозначим
![]() .
.
Рассмотрим
последовательность функций
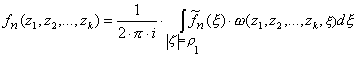 , (10)
, (10)
где
![]() , n = 1, 2,…
, n = 1, 2,…
Из (10) на основании свойств функции ![]() , вытекает, что последовательность
, вытекает, что последовательность ![]()
![]() элементов пространства
элементов пространства ![]() сходится равномерно на каждом компакте пространства Сk. Следовательно, в силу сделанного предположения,
предельная функция последовательности (10) -
сходится равномерно на каждом компакте пространства Сk. Следовательно, в силу сделанного предположения,
предельная функция последовательности (10) - ![]() принадлежит пространству
принадлежит пространству ![]() . В таком случае, так как оператор Т непрерывен, функция
. В таком случае, так как оператор Т непрерывен, функция ![]() принадлежит AR.
Получили противоречие.
принадлежит AR.
Получили противоречие.
Зададим в пространстве ![]() норму по формуле (11):
норму по формуле (11):
![]()
![]() ,
, ![]()
где
Т – оператор (7). Метрика (12):
![]()
индуцирует
в пространстве ![]() топологию, с которой
это пространство превращается в пространство типа Фреше. Отметим, что оператор
(7), отображающий пространство
топологию, с которой
это пространство превращается в пространство типа Фреше. Отметим, что оператор
(7), отображающий пространство ![]() с метрикой (12) в пространство AR, устанавливает линейный гомеоморфизм.
с метрикой (12) в пространство AR, устанавливает линейный гомеоморфизм.
Далее, говоря о ![]() как о топологическом
пространстве, будем предполагать, что топология
как о топологическом
пространстве, будем предполагать, что топология ![]() индуцирована метрикой
(12).
индуцирована метрикой
(12).
4. Линейные функционалы, линейные операторы и базисы
в пространствах ![]()
Пусть функционал L, определенный в пространстве ![]() линеен, то есть для
линеен, то есть для
![]() и
и ![]() ,
, ![]() ,
,
и
пусть ![]() ,
, ![]() .
.
Теорема 4.1.
Для того, чтобы функционал L был
непрерывным, необходимо и достаточно, чтобы выполнялось условие:
![]() (13)
(13)
Доказательство.
Так как пространства ![]() и АR линейно
гомеоморфны, то функционал L будет
непрерывным тогда и только тогда, когда будет непрерывным в пространстве АR функционал
и АR линейно
гомеоморфны, то функционал L будет
непрерывным тогда и только тогда, когда будет непрерывным в пространстве АR функционал
![]() . Так как
. Так как
![]() ,
,
то
необходимым и достаточным условием непрерывности функционала ![]() является условие:
является условие:
![]() ,
,
(см.
[2], стр. 118), которое равносильно (13). Из этой теоремы вытекает, что формула
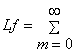
![]()
![]() , (14)
, (14)
где
![]() - любая совокупность комплексных чисел, удовлетворяющая (13)
задает общий вид линейного функционала в пространстве
- любая совокупность комплексных чисел, удовлетворяющая (13)
задает общий вид линейного функционала в пространстве ![]() ; сходимость ряда в (14) абсолютная. Функционал (14)
допускает интегральное представление
; сходимость ряда в (14) абсолютная. Функционал (14)
допускает интегральное представление
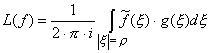 ,
, ![]() ,
,
где ![]() ,
, ![]()
![]()
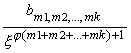 ,
,
функция
![]() аналитична в области
аналитична в области ![]() .
.
По
той же схеме, что и теорема 4.1 доказываются следующие утверждения.
Теорема 4.2. Любой
базис пространства ![]() получается из степенного
получается из степенного
![]() ,
, ![]() ,
,
путем:
1.
Перестановки функций
степенного базиса, соответствующей какой-либо биекции множества N k, на себя;
2.
Умножения каждой
функции степенного базиса на число, отличное от нуля;
3.
Применения линейного
автоморфизма к пространству ![]() (см. [2], стр. 179).
(см. [2], стр. 179).
Пусть S – оператор,
отображающий ![]() в
в ![]() линеен и пусть
линеен и пусть
![]() ,
, ![]() ,
,
![]() .
.
Теорема 4.3.
Для того чтобы оператор S был непрерывен
необходимо и достаточно, чтобы для каждого ![]() ,
, ![]() , существовали такие положительные числа
, существовали такие положительные числа ![]() и
и ![]() , что
, что
![]() при
при ![]() .
.
Литература
[1]. Мануилов Н.Ф. Исследование линейных отображений
пространства аналитических функций двух переменных // Сб. Кирилло-Мефодиевские
чтения, - Смоленск, 2004.
[2]. Маркушевич А.И. Избранные главы теории
аналитических функций. – М.: Наука, 1976.
[3]. Мануилов Н.Ф. О пространстве голоморфных
отображений // Некоторые вопросы теории полианалитических функций и их
обобщений. – Смоленск, СГПИ, 1991.
[4]. Рыбников К.А. Введение в комбинаторный анализ,
М.: МГУ, 1985.
[5]. Меньшиков М.В. и др. Комбинаторный анализ. Задачи
и упражнения (Под ред. К.А. Рыбникова). – М.: Наука, главная ред.физ. –мат.
литературы, 1982.
Linear functionals and
operators in space of sedate numbers with quickly decreasing factors
Manuilov N. F.
The work is devoted to research
of linear displays of spaces of the whole analytical functions of many complex
variables set by sedate numbers with quickly decreasing factors. The topology
in which such space is space and type Freshe is certain. Linear functional the
general view is found in space of the specified type, the description of linear
displays from one space in another and bases in such spaces is given.
Key words: analytical function, a sedate series with
rapidly factors, a linear functional, a linear operator, spaces of type Freshe,
base in a vector space.
Смоленский гуманитарный университет
Поступила 15.04.2010.