Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 2. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm

УДК 623.418.2

ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ЗАДАННУЮ ЦЕПЬ С МИНИМАЛЬНЫМИ ИСКАЖЕНИЯМИ

Ó 2010 г. Василевский А. В.

(vasilevskiy.doc)

В настоящее время определенные трудности возникают при решении задачи синтеза сигналов, претерпевающих минимальные искажения при прохождении через заданную цепь. В статье рассмотрена возможность получения таких сигналов, оптимальных в смысле минимальных искажений, с помощью устройства с цепью корреляционной обратной связи.

Ключевые слова: ошибка, оптимальный сигнал, цепь корреляционной обратной связи

Постановка задачи имеет следующую формулировку.

Дана цепь с известной комплексной передаточной функцией (комплексной частотной характеристикой) .

Требуется найти сигнал , искажения которого в этой цепи будут минимальными (рис. 1).

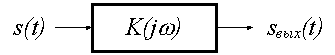
Рис. 1. Постановка задачи синтеза сигнала, претерпевающего минимальные искажения при прохождении через цепь с заданной комплексной

передаточной функцией (комплексной частотной характеристикой)

Такая задача может иметь практическое значение в ситуации, когда изменение характеристики цепи не представляется возможным или связано со значительными затруднениями, а на сигнал жестких ограничений не накладывается.

Для решения задачи в наилучшей форме, или нахождения сигнала, претерпевающего в заданной цепи наименьшие искажения, предварим решение задачи выбором показателя качества и критерия оптимальности.

Искажения сигнала в цепи минимальны, если минимальна разность сигналов на входе и на выходе цепи. Эту разность удобно назвать ошибкой и определить ее выражением

.

Такая ошибка в широком классе сигналов случайна. Она может принимать как положительные, так и отрицательные значения. Ее характеристики (закон распределения , спектральная плотность мощности, корреляционная функция) будет зависит от формы используемого сигнала. Однако с большой степенью уверенности можно предположить, что среднее значение ошибки будет равно нулю. Такое предположения обосновано тем, что в цепях реальных устройств, как правило, в тракте прохождения сигналов имеются разделительные емкостей и согласующие трансформаторы, которые препятствуют прохождению постоянной составляющей сигнала.

«Величину» ошибки (разброс ее значений, или мощность ошибки) характеризует дисперсия ошибки , определяемая выражением

.

Черта сверху означает усреднение.

При наименьших искажениях сигнала в цепи разброс значений ошибки будет минимальный, так же как и минимальны отклонения значений этой ошибки от нулевого уровня. Это соответствует минимальной дисперсии ошибки. Поэтому наилучшим, или оптимальным в заданных условиях следует считать сигнал, при поступлении которого на вход данной цепи дисперсия ошибки будет минимальна.

Следует отметить, что в литературе имеются сведения об использовании таких показателей при решении схожей задачи – при анализе оптимальных фильтров для случайных сигналов [1]. Однако в этой задаче, в отличие от рассматриваемой, искомой является характеристика фильтра, а не сигнал.

Таким образом, при решении поставленной задачи наилучшим образом, или при выборе сигнала, оптимального в смысле наименьших искажений, показателем качества сигнала является ошибка, а критерием его оптимальности – минимум дисперсии этой ошибки.

С учетом введенных выражений для ошибки и ее дисперсии, схема получения сигнала ошибки и ее дисперсии может быть представлена в виде, приведенном на рис. 2.

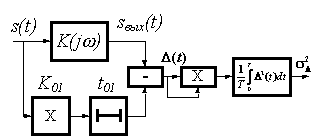
Рис. 2. Схема получения сигнала ошибки с устранением систематической составляющей и вычислением дисперсии ошибки.

Схема содержит:

заданную цепь с известной комплексной передаточной функцией ;

усилитель с постоянным коэффициентом усиления К₀₁;

линию задержки с постоянной задержкой на время t₀₁;

вычитатель (схему получения ошибки );

перемножитель (схему возведения ошибки в квадрат);

вычислитель среднего значения квадрата ошибки, или дисперсии ошибки .

Усилитель с постоянным коэффициентом усиления К₀₁ и линия задержки с постоянной задержкой на время t₀₁ учитывают постоянное усиление и задержку сигнала в цепи, что необходимо учесть при вычислении ошибки (для устранения ее систематической составляющей). Величины К₀₁ и t₀₁ при заданной характеристике цепи следует считать постоянными и известными.

Ошибка формируется на выходе вычитателя по результатам сравнения входного сигнала, скорректированного по усилению и задержке, и входного сигнала, прошедшего заданную цепь.

После возведения ошибки в квадрат вычисляется среднее значение этого квадрата, т.е. дисперсия ошибки.

Параметры сигнала, при которых дисперсия минимальна, будут оптимальными в заданных условиях решения задачи.

Рассмотри возможность непосредственного формирования сигнала, отвечающего выбранному критерию оптимальности. Для этого используем схемное решение, позволяющее провести оптимизацию параметров сигнала с помощью коррелятора.

Известны устройства с цепью корреляционной обратной связи, обеспечивающие минимальную мощность выходного сигнала (например, [2]). Применительно к решаемой задаче схема формирования оптимального сигнала может иметь вид, приведенный на рис. 3.

Отметим, что приведенная схема соответствует обработке комплексных амплитуд и предусматривает при ее реализации применение квадратурных каналов.

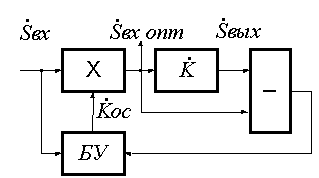
Рис. 3. Схема формирования оптимального сигнала.

Схема содержит:

заданную цепь с комплексным коэффициентом передачи ;

перемножитель:

блок управления (БУ);

вычитатель.

Цепь обратной связи формирует управляющее напряжение с комплексной амплитудой . В установившемся режиме блок управления формирует управляющее напряжении, при котором мощность напряжения на выходе вычитателя (в нашем случае – мощность ошибки) минимальна, что соответствует оптимальным параметрам искомого сигнала, который формируется на выходе перемножителя.

Схема и алгоритм работы блока управления зависят от типа и характеристик сигнала

Для получения оптимального по условию задачи сигнала, на вход цепи следует подать предварительно выбранный сигнал, близкий к искомому (например, согласованный с заданной цепью). На выходе перемножителя после завершения переходных процессов в схеме можно наблюдать сигнал, искажения которого в данной цепи будут минимальны, т.е. искомый оптимальный сигнал.

Параметры сформированного в схеме сигнала можно использовать для последующего формирования его копии или близкого аналога и решения таким способом задачи формирования теперь уже известного сигнала, оптимального в рассматриваемом смысле.

Возможности компьютерного моделирования позволяют решать поставленную задачу в широком классе характеристик цепей.

Таким образом, применение устройств с цепью корреляционной обратной связи позволяет при известной характеристике цепи решить задачу нахождения сигнала, оптимального в смысле его минимальных искажений в данной цепи.

литература

1. Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высш. шк., 2003. – 462 с.

2. Радиоэлектронные системы: основы построения и теория. Справочник. Под ред. Я.Д.Ширмана. М., МАКВИС, 1998. – 828с.

SIGNAL PASSAGE OVER A SPECIFIED CIRCUIT WITH MINIMUM DISTORTIONS

Vasilevskiy А.

Presently there certain difficulties, arise at the decision of a signal design problem when the signals are exposed to the minimal distortions at passage over a specified circuit. The lecture is referred to the availability of such signals optimum in the context of minimum distortions using the device of correlation feedback circuit.

Key words: distortions, signals optimum, the device of correlation feedback circuit

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

 имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 28.05.2010.