Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 4. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-28-html/TITL-28.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-28-html/cont.htm
УДК 37.0:004
ББК 74.580.255
Построение графовых моделей
теоретического материала
Ó
2010 г. Бояринов Д. А.
В статье рассматривается подход к построению
графовой модели теоретического материала.
Ключевые
слова: граф,
графовая модель.
Создание информационного
образовательного пространства одним из необходимых условий имеет разработку
средств и методов построения формального описания будущего контента этого
пространства, в частности теоретического материала учебных дисциплин. Мы
полагаем, что значительным потенциалом в данной сфере обладает моделирование
средствами теории графов.
Использование графовых
моделей в педагогике к настоящему моменту предлагалось многими авторами. Можно
говорить о существовании определенных традиций графового моделирования в этой
области.
В работах Л. М. Фридмана [8]
и Б. К. Дамитова были практически реализованы следующие направления
использования графовых моделей:
·
как
язык записи алгоритмов решения задач на распознавание принадлежности к тому или
иному виду;
·
как
метаязык тернарных задач (в этом качестве использовались трёхвершинные графы);
·
для
решения физических задач, как язык описания структуры задачи (в этом качестве
использовались граф-схемы).
В работе В. П. Мизинцева
предлагался подход к измерению трудности и сложности задач, основанный на использовании
графовых моделей [1; 7]. Оригинальной чертой данного подхода является
рассмотрение в качестве значимых характеристик графа, не сохраняющихся при
изоморфизмах (т.е. не являющихся инвариантами теории графов). Недостатки
подобного подхода были подробно проанализированы Р. А. Гильмановым [1].
Д. В. Долгих в своём
диссертационном исследовании предлагал использование графовых моделей структуры
теоретического материала курса лекций. Модель представляла собой
ориентированный мультиграф. Вершины графа (узлы) – разделы учебного материала.
При этом предлагалось разделить все вершины на несколько категорий:
·
ядро
знаний – учебный материал, входящий в курс лекций;
·
дополнительные
знания – учебный материал, не входящий в курс лекций, но относящийся к темам,
изучаемым в рамках данной дисциплины;
·
окружение
ядра – вся совокупность дополнительных знаний.
Принцип модульного
структурирования материала в качестве ведущего принципа внедрения новых
информационных технологий в процесс обучения декларируется в работе М. В. Лось
[5]. Это, в свою очередь является предпосылкой для построения графовой модели
теоретического материала.
Применение графовых моделей
для представления внутренней структуры отдельных тем школьного курса математики
предлагается в работах Н. И. Зильберберга на протяжении примерно 20 лет [4].
В работах О. Б. Епишевой и
В. И. Крупич [3] предлагается использование графовых моделей (деревьев) для
отображения и анализа структуры решения некоторых геометрических задач как
подход к решению проблемы сложности / трудности.
В современных работах, в
частности трудах С. П. Грушевского, А. И. Архиповой, Д. В. Долгих, Е. М.
Лященко [2; 6] также предлагается использование графовых моделей прежде всего
как средство отображения логической структуры теоретического материала по данной
теме. В работе [2], помимо вышесказанного, графовые модели использовались при
конструировании фасетных тестов по математике.
В
целом к настоящему моменту в педагогике существует достаточно отработанная
схема построения графовых моделей теоретического материала по данной теме. Общая
основа построения семантической сети: вершинам графа сопоставлены понятия
(объекты, события, процессы), а дугам – отношения на множестве понятий.
Для
построения модели требуется [4]:
а)
разобрать математическое содержание отобранного материала;
б)
разбить материал на логически завершенные и самостоятельные части;
в)
выявить логические связи частей;
г)
выделить в тексте структурные элементы (определения, утверждения, алгоритмы,
иллюстрации и т.п.) – элементы знания по данной теме;
д)
изучить характер логических обоснований различных частей;
е)
соотнести упражнения с выделенными в пункте б) частями.
На графовой модели вершины
графа соответствуют элементам знания по данной теме, дуги – наличию между
элементами знания причинно-следственных связей (ребро, связывающее две вершины,
отражает логические, причинно-следственные связи между соответствующими
элементами знания).
Под элементами знания
понимается все понятия, определения, алгоритмы, формулы, аксиомы, теоремы,
которые в совокупности образуют основу теоретического материала по данной теме
и усвоение которых требуется обязательными стандартами обучения.
Граф является ориентированным
в силу специфики причинно-следственных связей.
Проиллюстрируем данные
положения на материале школьного курса математики, отметив вместе с тем, что
данный язык моделирования инвариантен содержанию предметной области (в данном
случае, теоретическому материалу по данной теме).
Пример графовой модели
материала темы «квадратные уравнения» приведен на рисунке 1.
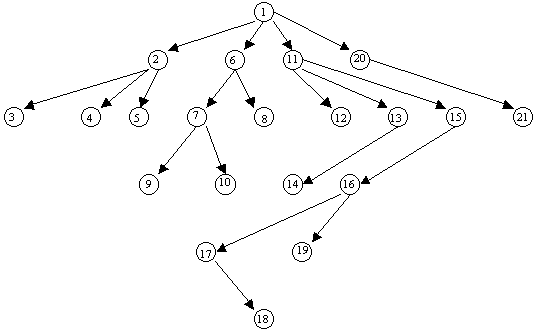

Рис. 1. Графовая модель теоретического материала
темы «Квадратные уравнения»:
В вышеприведенной схеме
номерам вершин графа соответствуют следующие элементы знания:
1 - определение квадратного
уравнения;
2 - уравнение вида x![]() =d;
=d;
3 - d>0 – два
действительных корня;
4 - d=0 – корень 0;
5 d<0 – нет
действительных корней;
6 - неполные квадратные
уравнения;
7 - уравнение вида a*x![]() +c=0;
+c=0;
8 - уравнение вида a*x![]() +bx=0, b≠0;
+bx=0, b≠0;
9 - c<0 – два
действительных корня;
10 - c=0 – корень 0;
11 - метод выделения полного
квадрата;
12 -b![]() -4ac<0 – действительных корней нет;
-4ac<0 – действительных корней нет;
13 - b![]() -4ac=0 – один действительный корень;
-4ac=0 – один действительный корень;
14 - формула корней
квадратного уравнения;
15 - b![]() -4ac>0 – два действительных корня;
-4ac>0 – два действительных корня;
16 - формула корней
квадратного уравнения;
17 - формула корней
приведенного квадратного уравнения;
18 - теоремы Виета (прямая и
обратная);
19 - формула корней
уравнения a*x![]() +2mx+c=0;
+2mx+c=0;
20 - определение квадратного
трехчлена;
21 - формула разложения на
множители.
В дальнейшем по мере
необходимости для решения конкретных задач могут строиться иные модели,
адаптированные под эти задачи (например, модель в виде графа со взвешенными
дугами).
Таким образом, с
использованием существующих разработок в области педагогики и теории обработки
информации возможно построение графовой модели материала по данной теме, что
является одним из инструментов отображения учебного материала в рамках
информационного образовательного пространства «средняя школа - вуз».
Литература
1. Гильманов Р. А. Проблема дидактометрии трудности
учебных упражнений. – Казань: Изд-во Казанского ун-та, 1989. – 182с.
2. Грушевский С. П., Архипова А. И. Проектирование
учебно-информационных комплексов: Учебная монография. – Краснодар, 2000. – 70
с.
3. Епишева О. Б., Крупич В. И. Учить школьников учиться
математике: Формирование приемов учебной деятельности: Книга для учителя. – М.:
Просвещение, 1990. – 127 с.
4. Зильберберг Н. И. Урок математики: Подготовка и
проведение: Кн. для учителя. – М.: Просвещение; АО «Учебная литература», 1966.
– 176 с.
5. Лось М. В. Школьный учебник и новые информационные
технологии обучения (на примере учебников математики). – Автореф. дис. на соиск. уч. ст. канд. пед.
наук. – Владикавказ, 1999.
6. Лященко Е. М. Интеграция управления обучением на основе
моделей и алгоритмов конструирования учебной информации и диагностики степени
обученности: Автореф. дис. на соиск. уч. ст.
д-ра пед. наук. – Воронеж, 2000.
7. Мизинцев В. П. Информационный анализ показателя
сложности и трудности учебной задачи // Вопросы преподавания физики в высшей
школе. – Хабаровск, 1976. – С. 132 – 186.
8. Фридман Л. М., Кулагина И. Ю. Психологический
справочник учителя. – М.: Просвещение, 1991. – 288 с.
THE CONSTRUCTION OF GRAPH MODELS
OF A THEORETICAL MATERIAL
Boyarinov D. A.
In the given article
the approach to the construction of graph models of a theoretical material is
considered.
Key
words: graph, graph model.
Исследование
выполнено в рамках научно-исследовательского проекта РГНФ ("Информационное
образовательное пространство "средняя школа - вуз"), проект
10-06-58605а/Ц.
Бояринов Дмитрий
Анатольевич
кандидат
педагогических наук, доцент
Кафедра информатики
Смоленский
Государственный Университет
Поступила в
редакцию 15.12.2010.