Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 2. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm
УДК 517.927
СИНГУЛЯРНАЯ
КРАЕВАЯ ЗАДАЧА ТИПА НИКОЛЕТТИ С КУСОЧНО-НЕПРЕРЫВНЫМИ РЕШЕНИЯМИ ДЛЯ СИСТЕМЫ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Ó 2011 г. Исраилов С. В.
В новом классе сингулярных систем дифференциальных уравнений сформулированы
и доказаны теоремы существования кусочно-непрерывных решений краевой задачи
типа Николетти.
Ключевые слова: сильносингулярные уравнения,
кусочно-непрерывные решения, задачи типа Николетти, существование решений.
1.
Будем изучать
систему дифференциальных уравнений в квазилинейной форме
![]() (1)
(1)
относительно
точек области ![]() известные числа. Предполагается, что функции
известные числа. Предполагается, что функции ![]()
![]() непрерывны по
совокупности аргументов в области
непрерывны по
совокупности аргументов в области ![]() , где
, где ![]() а при
а при ![]() имеют сингулярности в
смысле работ
имеют сингулярности в
смысле работ ![]() Для таких систем
подробно изучены вопросы существования, единственности и неединственности
непрерывных решений
Для таких систем
подробно изучены вопросы существования, единственности и неединственности
непрерывных решений ![]() дифференцируемых на интервалах
дифференцируемых на интервалах ![]() и удовлетворяющих
условиям задачи Николетти
и удовлетворяющих
условиям задачи Николетти ![]()
![]() (2)
(2)
где ![]() - данные числа из области
- данные числа из области ![]()
Характерной особенностью точки
сингулярности ![]() для функций
для функций ![]()
![]() в цитируемых работах
является ограниченность сверху или снизу функции
в цитируемых работах
является ограниченность сверху или снизу функции ![]() интегрируемыми (суммируемыми) или неинтегрируемыми (несуммируемыми) функциями на интервалах
интегрируемыми (суммируемыми) или неинтегрируемыми (несуммируемыми) функциями на интервалах ![]() и существование
функций
и существование
функций ![]()
![]() , непрерывных на
, непрерывных на ![]() и дифференцируемых на
и дифференцируемых на
![]() ,
,
удовлетворяющих
условиям ![]()
![]() , и таких, что
, и таких, что ![]()
функции
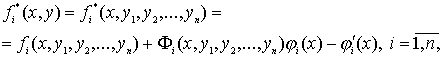 (3)
(3)
в области ![]() ограничены по модулю
интегрируемыми (суммируемыми) функциями на
ограничены по модулю
интегрируемыми (суммируемыми) функциями на ![]() т.е.
т.е.
![]() (4)
(4)
где ![]() при
при ![]() и
и
![]()
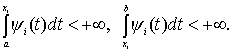 (5)
(5)
Такой класс сингулярных
дифференциальных уравнений удобно назвать слабосингулярными, имея ввиду
существование другого класса сингулярных дифференциальных уравнений ![]() , обладающих только
решениями с разрывами первого рода в
точках сингулярностей.
, обладающих только
решениями с разрывами первого рода в
точках сингулярностей.
Например,
система
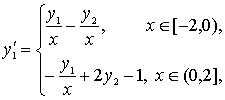
имеет
единственное решение
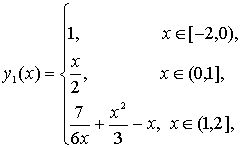
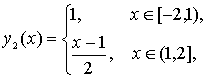
удовлетворяющее условиям
![]()
В соответствии с этим в новом классе
сингулярных дифференциальных уравнений условия задачи Николетти (2), естественно?
распадаются на краевые условия вида
![]() (6)
(6)
где ![]() - известные числа, причем
- известные числа, причем ![]()
Задачу (1), (6) в дальнейшем будем
называть краевой задачей типа Николетти. Вектор-функция ![]() считается решением этой задачи, если она непрерывна на интервалах
считается решением этой задачи, если она непрерывна на интервалах
![]() , ее
, ее ![]() -ая компонента
-ая компонента ![]() непрерывно дифференцируема на интервалах
непрерывно дифференцируема на интервалах ![]() функции
функции ![]() удовлетворяют системе
(1) на множестве
удовлетворяют системе
(1) на множестве ![]() и условиям (6). Особой
чертой сильносингулярной системы (1) является выполнимость неравенств (4),
когда присутствующие в них функции
и условиям (6). Особой
чертой сильносингулярной системы (1) является выполнимость неравенств (4),
когда присутствующие в них функции ![]() , непрерывны на
, непрерывны на ![]() имеют интегрируемые производные
имеют интегрируемые производные ![]() на этих же интервалах
и удовлетворяют условиям
на этих же интервалах
и удовлетворяют условиям
![]() (7)
(7)
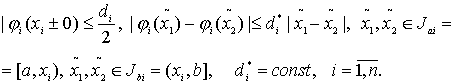
Если в приведенном выше примере положить
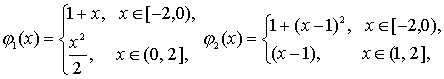
в любой области ![]() будут выполняться
условия вида (4) с интегрируемыми на
будут выполняться
условия вида (4) с интегрируемыми на ![]() функциями
функциями ![]()
Здесь функции ![]() таковы, что
выполняются равенства
таковы, что
выполняются равенства
![]()
2.
Теперь сформулируем
теоремы о разрешимости поставленной задачи.
Т е о р е м а 1. Пусть в области ![]() выполнены неравенства
(4), (5),
выполнены неравенства
(4), (5),
![]() (8)
(8)
где ![]() интегрируемые функции
в смысле Римана на
интегрируемые функции
в смысле Римана на ![]() и
и
![]() (9)
(9)
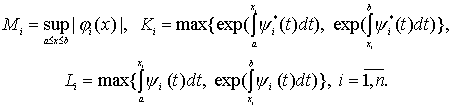 (10)
(10)
Тогда задача (1), (6) имеет по крайней мере одно решение.
Т е о р е м а 2. Пусть в области ![]() выполнены неравенства
(4), (5),
выполнены неравенства
(4), (5),
![]() (11)
(11)
где
![]() , неинтегрируемые функции на
, неинтегрируемые функции на ![]() такие, что для любого
такие, что для любого
![]()
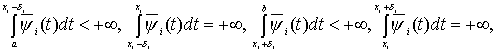 (12)
(12)
![]() , (13)
, (13)
где ![]() некоторые произвольные постоянные.
некоторые произвольные постоянные.
Тогда задача (1), (6) имеет континуум решений.
Т е о р е м а 3. Пусть в области ![]() выполнены неравенства
(4), (5), (8) при
выполнены неравенства
(4), (5), (8) при ![]() (11) при
(11) при ![]() и
и
![]() (14)
(14)
где
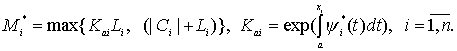 (15)
(15)
Тогда задача (1), (6) имеет континуум решений.
Т е о р е м а 4. Пусть в области ![]() выполнены неравенства
(4), (5), (11) при
выполнены неравенства
(4), (5), (11) при ![]() (8) при
(8) при ![]() и
и
![]() (16)
(16)
где
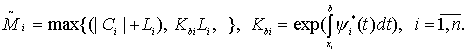 (17)
(17)
Тогда задача (1), (6) имеет
континуум решений.
З
а м е ч а н и е. Присутствие в
теоремах 2-4 произвольных постоянных
![]() , порождает переопределенность граничных условий. Возьмем точки
, порождает переопределенность граничных условий. Возьмем точки
![]() на сегменте
на сегменте ![]() , расположенные в порядке
, расположенные в порядке ![]() . Тогда в областях
. Тогда в областях ![]() правые части системы (1) будут ограничены соответственно
некоторыми числами
правые части системы (1) будут ограничены соответственно
некоторыми числами ![]() по модулям, т.е.
по модулям, т.е.
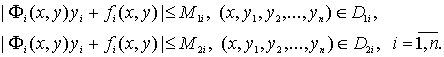 (18)
(18)
Запишем дополнительные
граничные условия
![]() (19)
(19)
![]() (20)
(20)
где ![]() - известные числа, причем
- известные числа, причем ![]() .
.
Т е о р е м а 5. Пусть в области ![]() , выполнены неравенства
, выполнены неравенства
![]() (21)
(21)
![]() (22)
(22)
где ![]()
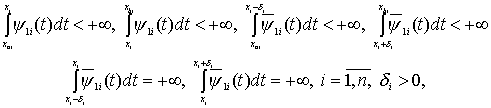 (23)
(23)
и
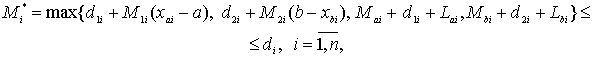 (30)
(30)
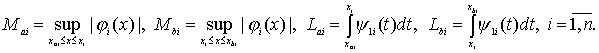 (31)
(31)
Тогда переопределенная сингулярная краевая задача (1), (6)
(19), (20) имеет по крайней мере одно решение.
Т е о р е м а 6. Пусть в области ![]() выполнены условия (4), (5), (8) теоремы 1, а в области
выполнены условия (4), (5), (8) теоремы 1, а в области ![]() условия (21), (22)
теоремы 5 с соответствующими ограничениями на функции
условия (21), (22)
теоремы 5 с соответствующими ограничениями на функции ![]() в (10), на функции
в (10), на функции ![]() ,
, ![]() в (23) на соответствующих
интервалах изменения
в (23) на соответствующих
интервалах изменения ![]() .
.
Тогда при выполнении
неравенств
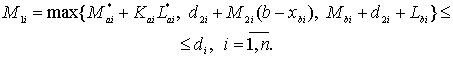 (32)
(32)
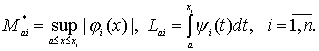 (33)
(33)
переопределенная сингулярная
краевая задача (1), (6), (20) имеет по крайней мере одно решение.
Т е о р е м а 7. Пусть в области ![]() выполнены условия (4), (5), (8) теоремы 1, а в области
выполнены условия (4), (5), (8) теоремы 1, а в области ![]() условия (21), (22) с соответствующими ограничениями на функции
условия (21), (22) с соответствующими ограничениями на функции ![]() в (10), на функции
в (10), на функции ![]() ,
, ![]() в (23) на
соответствующих интервалах изменения
в (23) на
соответствующих интервалах изменения ![]() .
.
Тогда
при выполнении неравенств
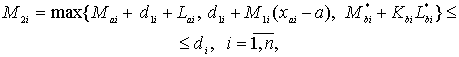 (34)
(34)
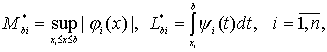 (35)
(35)
переопределенная сингулярная
краевая задача (1), (6), (19) имеет по крайней мере одно решение.
3.
Для доказательства
этих теорем строятся следующие системы интегральных уравнений:
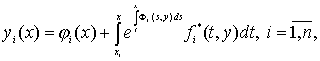 (36)
(36)
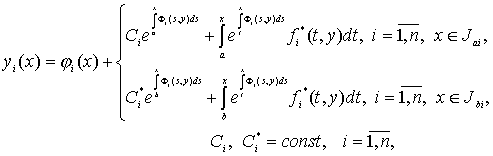 (37)
(37)
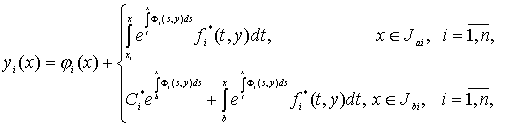 (38)
(38)
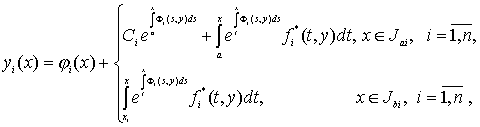 (39)
(39)
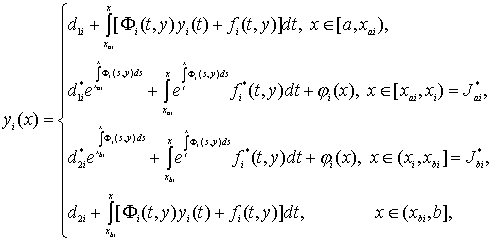 (40)
(40)
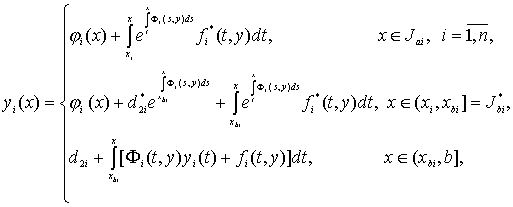 (41)
(41)
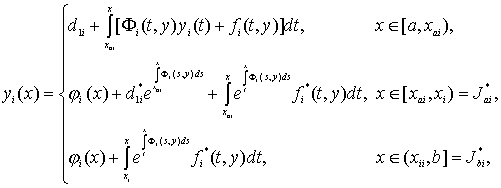 (42)
(42)
где
![]() (43)
(43)
4.
Покажем, как
строятся доказательства теорем. Для теоремы 1 соответствует система
интегральных уравнений (36), правые части которой определены в области ![]() . По условиям (4), (8) путем оценки их интегральных выражений
можно найти функции
. По условиям (4), (8) путем оценки их интегральных выражений
можно найти функции
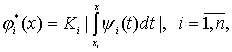 (44)
(44)
удовлетворяющие
условиям ![]() Возьмем пространство
Возьмем пространство ![]() кусочно-непрерывных
на сегменте
кусочно-непрерывных
на сегменте ![]() вектор-функций
вектор-функций ![]() с нормой
с нормой ![]() и соответствующей
метрикой
и соответствующей
метрикой![]()
для
любых вектор-функций ![]() из
из ![]() . Расстояние
. Расстояние ![]() удовлетворяет всем аксиомам метрики и сходимость в
удовлетворяет всем аксиомам метрики и сходимость в ![]() есть равномерная
сходимость почти всюду
есть равномерная
сходимость почти всюду ![]() . Нетрудно проверить, что пространство
. Нетрудно проверить, что пространство ![]() полно в смысле
сходимости по норме, т.е. являются банаховым. Обозначим через
полно в смысле
сходимости по норме, т.е. являются банаховым. Обозначим через ![]() множество функций
множество функций ![]() , непрерывных на
, непрерывных на ![]() и имеющих точку разрыва первого рода только при
и имеющих точку разрыва первого рода только при ![]() . Ясно, что
. Ясно, что ![]() . Возьмем множество
. Возьмем множество ![]() таких вектор-функций
таких вектор-функций ![]() из
из ![]() , что
, что
![]() , (45)
, (45)
и
для любого ![]() существует такое
число
существует такое
число ![]() , что при
, что при ![]()
![]() выполняются
неравенства
выполняются
неравенства
![]() . (46)
. (46)
Из (44) следует, что
![]() (47)
(47)
Поэтому для любого ![]() можно указать такое
можно указать такое ![]() , что
, что
![]() .
(47*)
.
(47*)
Положим
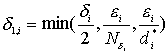 и
и ![]() . Так как
. Так как ![]() то
то ![]()
одновременно
попадают либо в интервалы ![]() , либо в сегменты
, либо в сегменты ![]() . Если
. Если ![]() , то в силу (45), (47*) и (7) для
, то в силу (45), (47*) и (7) для ![]() имеем
имеем
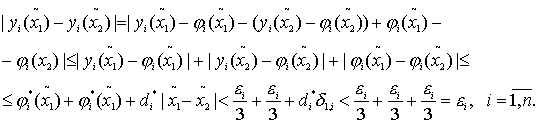 (48)
(48)
Если ![]() , то из-за (46) получим
, то из-за (46) получим
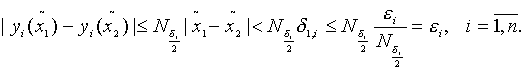 (49)
(49)
Таким образом
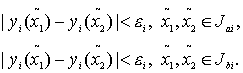 (50)
(50)
Разобьем отрезок ![]() точками деления
точками деления ![]()
![]() на части так, чтобы
выполнилось неравенство
на части так, чтобы
выполнилось неравенство ![]() , и зафиксируем эти точки деления. Возьмем любую
вектор-функцию
, и зафиксируем эти точки деления. Возьмем любую
вектор-функцию ![]() и поставим ей в
соответствии ступенчатую вектор-функцию
и поставим ей в
соответствии ступенчатую вектор-функцию ![]() определенную
следующим образом:
определенную
следующим образом:
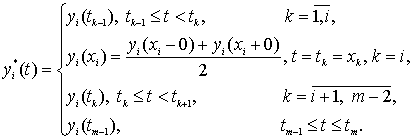 (51)
(51)
Из-за
неравенств (50) внутри каждого открытого интервала ![]() , колебание функции
, колебание функции ![]() меньше
меньше ![]() , поэтому
, поэтому ![]() Следовательно, множество
Следовательно, множество
![]() , составленное из всех функций
, составленное из всех функций ![]() , соответствующих
, соответствующих ![]() вектор-функции
вектор-функции ![]() из пространства
из пространства ![]() , образует
, образует ![]() -сеть для
-сеть для ![]() х компонент вектор-функций из
х компонент вектор-функций из ![]()
Рассмотрим теперь множество ![]() ступенчатых функций
ступенчатых функций ![]() . Каждая ступенчатая функция
. Каждая ступенчатая функция ![]() однозначно определяется
однозначно определяется
![]() числами – своими
значениями в фиксированных точках
числами – своими
значениями в фиксированных точках ![]() . Принимая эти числа за координаты точек из
. Принимая эти числа за координаты точек из ![]() мерного евклидова пространства
мерного евклидова пространства ![]() , установим взаимнооднозначное соответствие между множеством
, установим взаимнооднозначное соответствие между множеством ![]() и некоторым
множеством
и некоторым
множеством ![]() . Множество
. Множество ![]() ограничено, так как
для любой точки
ограничено, так как
для любой точки ![]()
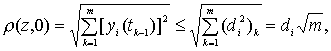 (52)
(52)
если учесть ![]()
Так как ![]() ограниченное множество
ограниченное множество ![]() мерного евклидова пространства,
то
мерного евклидова пространства,
то ![]() компактно. Но тогда
компактно и
компактно. Но тогда
компактно и ![]() в смысле равномерной
сходимости на
в смысле равномерной
сходимости на ![]() , так как, если
, так как, если ![]() и
и ![]() - функции, соответствующие
- функции, соответствующие ![]() , то
, то
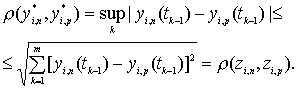 (55)
(55)
Поэтому
сходимость последовательности ![]() влечет за собой равномерную сходимость соответствующей
последовательности
влечет за собой равномерную сходимость соответствующей
последовательности ![]() и компактность множества
и компактность множества
![]() доказана.
доказана.
Если вместо ![]() и
и ![]() взять соответственно
взять соответственно ![]() , то все вышеприведенные рассуждения справедливы для всех
значений
, то все вышеприведенные рассуждения справедливы для всех
значений ![]() и прямое топологическое произведение
и прямое топологическое произведение ![]() и компактно, причем является
и компактно, причем является
![]() окрестностью для
окрестностью для ![]() . Поэтому
. Поэтому ![]() также компактно в
также компактно в ![]() , так как функции
, так как функции ![]() из-за (9), (44), (45) равномерно ограничены:
из-за (9), (44), (45) равномерно ограничены:
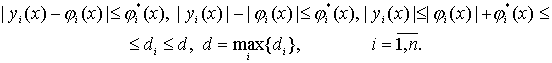 (56)
(56)
Покажем, что множество ![]() замкнуто и выпукло. Пусть
замкнуто и выпукло. Пусть
![]()
![]() и
и ![]() . Тогда из (45),
(44), (9)
. Тогда из (45),
(44), (9)
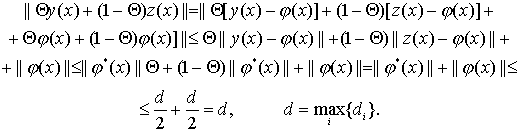 (57)
(57)
Т.е. ![]() выпукло. Пусть последовательность
выпукло. Пусть последовательность ![]() сходится к
сходится к ![]() равномерно при
равномерно при ![]() . В силу тех же условий имеем
. В силу тех же условий имеем
![]()
![]() для достаточно
большого
для достаточно
большого ![]() и произвольного
и произвольного ![]() . Отсюда
. Отсюда ![]() и множество
и множество ![]() замкнуто, еще из (58) следует
замкнуто, еще из (58) следует ![]() .
.
Рассмотрим теперь нелинейный
интегральный оператор ![]() , где
, где ![]() ,
,
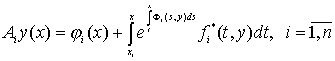 , (59)
, (59)
из
правых частей (36). В силу неравенств ![]() , (см. (44), (56)) оператор А определен на
, (см. (44), (56)) оператор А определен на ![]() . Покажем, что А
. Покажем, что А![]()
![]()
![]() . Из условий (4), (8)-(10) получаем (см.(44))
. Из условий (4), (8)-(10) получаем (см.(44))
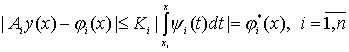 . (60)
. (60)
Возьмем достаточно малое
число ![]() и пусть
и пусть ![]() . Тогда по (59) можно составить разность
. Тогда по (59) можно составить разность
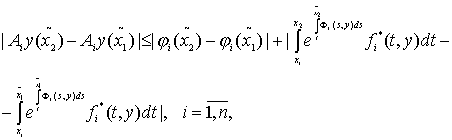 (61)
(61)
откуда (см.(4), (7), (8))
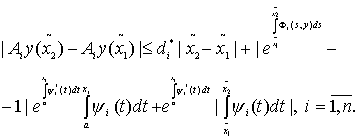 (62)
(62)
Далее,
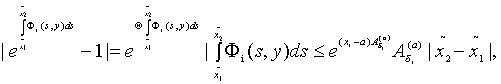
где
![]() (64)
(64)
Поэтому из (62) имеем оценки
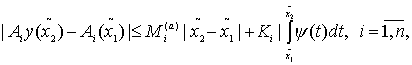 (65)
(65)
где
![]() (66)
(66)
Положим
![]() (67)
(67)
и запишем (65) в виде
![]() . (68)
. (68)
Точно так же при ![]() получим из (59)
получим из (59)
![]() , (69)
, (69)
где
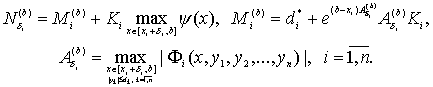 (70)
(70)
Таким образом, из (68), (69) окончательно получим
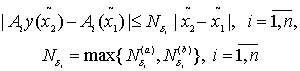 (71)
(71)
Итак, оператор А
преобразует ![]() в себя.
в себя.
Остается доказать непрерывность
оператора на ![]() . Пусть последовательность
. Пусть последовательность ![]()
![]() равномерно сходится к вектор-функции
равномерно сходится к вектор-функции ![]() Пусть
Пусть ![]() достаточно малое число. По (59) составим разность для
достаточно малое число. По (59) составим разность для ![]() и оценим их с помощью
условий (4), (8)-(10)
и оценим их с помощью
условий (4), (8)-(10)
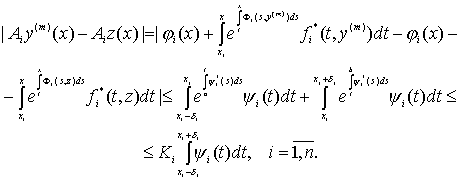 (72)
(72)
Ясно, что число ![]() в (72) можно
подобрать так, чтобы для любого данного числа
в (72) можно
подобрать так, чтобы для любого данного числа ![]() выполнялось бы
неравенство
выполнялось бы
неравенство
![]() . (73)
. (73)
Пусть теперь ![]() . Из-за отсутствия точек сингулярностей на этих отрезках для
достаточно больших
. Из-за отсутствия точек сингулярностей на этих отрезках для
достаточно больших ![]() осуществляются неравенства:
при
осуществляются неравенства:
при ![]()
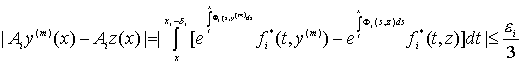 , (74)
, (74)
при ![]()
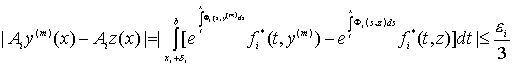 . (75)
. (75)
Это
объясняется возможностью предельного перехода под знаком интегралов в (74),
(75) в силу ограничений на ![]() в условиях теоремы 1. С учетом (73) – (75) для
в условиях теоремы 1. С учетом (73) – (75) для ![]() можно записать
можно записать
![]() (76)
(76)
т.е.
оператор А непрерывен на ![]() . Следовательно, непрерывный оператор А преобразует компактное, замкнутое, выпуклое множество
. Следовательно, непрерывный оператор А преобразует компактное, замкнутое, выпуклое множество ![]() в себя и в силу
принципа Шаудера
в себя и в силу
принципа Шаудера ![]() имеет в
имеет в ![]() неподвижную точку,
что равносильно существованию решения системы интегральных уравнений (36). Ее решения дифференцируемы при
неподвижную точку,
что равносильно существованию решения системы интегральных уравнений (36). Ее решения дифференцируемы при ![]() , что можно показать непосредственным вычислением производных
(составляется конечноразностное отношение, применяется теорема о среднем и
осуществляется переход к пределу). По методу получения системы (36) каждое ее
решение
, что можно показать непосредственным вычислением производных
(составляется конечноразностное отношение, применяется теорема о среднем и
осуществляется переход к пределу). По методу получения системы (36) каждое ее
решение ![]()
![]() является и решением сингулярной системы (1) и из выполнения
неравенств
является и решением сингулярной системы (1) и из выполнения
неравенств ![]() (см. (7), (45))
следует и выполнение граничных условий
(см. (7), (45))
следует и выполнение граничных условий ![]() . Теорема 1 доказана. Аналогично доказываются и теоремы 2-7 с
использованием соответствующих систем интегральных уравнений (37)-(42).
. Теорема 1 доказана. Аналогично доказываются и теоремы 2-7 с
использованием соответствующих систем интегральных уравнений (37)-(42).
Литература
1.
Чечик В.А. Исследование
систем обыкновенных дифференциальных уравнений с сингулярностью //Тр. Московского матем.общества, 1959.
Т.8., С.155-198.
2.
Исраилов С.В. О
сингулярной многоточечной краевой задаче //Уч.записки Азерб. Гос.ун-та. Серия
физ-мат.науки. 1963, №3. С.63-71.
3. Кигурадзе И.Т. Некоторые сингулярные краевые задачи
для обыкновенных дифференциальных уравнений. Тбилиси: изд. Тбилисского ун-та,
1975. С.
352.
4.
Nicoletti O. Sulle condizioni iniziali
che determiniano gle integrali della
differenziali ordinazie. – Atti della R. Acc. Sc. Torino. 1897, 1898. 748-759.
5.
Исраилов С.В., Ющаев
С.С. Многоточечные и функциональные краевые задачи для обыкновенных
дифференциальных уравнений. Нальчик, Издательский центр «Эль-фа», 2004. С.445.
6.
Исраилов С.В. Система
дифференциальных уравнений с многоточечной сингулярностью и разрывными
решениями. Дифференциальных уравнений и их приложения. Межвузовский сборник
научных трудов. Изд-во Саратовского университета, 1993, С.42-51.
7.
Исраилов С.В., Сагитов
А.А. Решение сингулярных ОДУ ![]() го порядка с кусочно-непрерывными производными
го порядка с кусочно-непрерывными производными ![]() -го порядка //Функционально-дифференциальные уравнения и их
приложения. Материалы 4-й Международной
конференции, 21-24 сентября 2009г., Махачкала. С.128-130.
-го порядка //Функционально-дифференциальные уравнения и их
приложения. Материалы 4-й Международной
конференции, 21-24 сентября 2009г., Махачкала. С.128-130.
8.
Исраилов С.В., Сагитов
А.А. Об одном классе сингулярных дифференциальных уравнений //Материалы
Всероссийской научно-технической конференции. Воронеж, 2-7 февраля 2009.
С.92-93.
9.
Очан Ю.С. Исследование
одного функционального пространства //Функциональный анализ и его применение.
Труды V Всесоюзной конференции
по функциональному анализу и его применению. Из-во АН. Аз.ССР, Баку, 1961.
С.215-219.
10. Люстерник Л.А., Соболев В.И. Краткий курс
функционального анализа. М. 1981.
singuljarnyh THE
REGIONAL PROBLEM OF TYPE NIKOLETTI WITH KUSOCHNO-CONTINUOUS DECISIONS FOR
SYSTEM OF THE ORDINARY DIFFERENTIAL EQUATIONS
Israilov S. V.
In new class of singular differential system. Existence theorems of piecewice continuous solutions of boundary
problem Nicolletti are proved.
Key words: strong singular equations, piecewice continuous, Nicolletti problem,
existence of solutions
Чеченский государственный
университет (ЧГУ)
Поступила в редакцию 21.02.2011