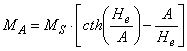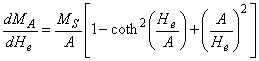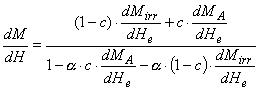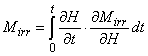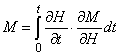Поступила в редакцию

Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 4. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/TITL-40.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/cont.htm

УДК 519.711.3

МЕТОД КОРРЕКЦИИ ФОРМЫ КРИВОЙ НАМАГНИЧИВАНИЯ В МОДЕЛИ ДЖИЛСА-АТЕРТОНА ФЕРРОМАГНИТНОГО СЕРДЕЧНИКА

Ó 2014 г. Каткова А. А., Пеньков А. А.

(katkova.doc)

В работе предложен метод коррекции формы кривой намагничивания в модели Джилса-Атертона ферромагнитного сердечника. Предлагаемый метод основан на введении в модель дополнительных уравнений. Для подтверждения улучшения формы петель проводится сравнение с экспериментальными характеристиками длямагнитопроводаК16х10х4,5 М2000НМ1 на частоте 100кГц.

Ключевые слова: модель Джилса-Атертона, сердечник, кривая намагничивания.

Разработка индуктивных элементов является трудоемким и сложным техническим процессом, требует длительного времени и значительных затрат. Актуальным решением задачи сокращения этапа испытаний становится моделирование. Такое моделирование основано на использовании SPICEи VHDL моделей, полученных на основе результатов измерений характеристик компонентов.

Программы схемотехнического моделирования используют различные языки описания: SPICE, HSpice, PSpice, AHDL, VHDL-AMS и др. Многие фирмы скрывают используемые при моделировании алгоритмы, что значительно затрудняет анализ достоверности результатов моделирования и делает невозможным усовершенствование моделей. Перспективными являются VHDL-модели, открытые для редактирования и обладающие обширными возможностями для добавления новых параметров и математических зависимостей.

Система автоматического проектирования SystemVision компании MentorGraphics обеспечивает поддержку языков SPICE, IBIS и VHDL-AMS в одной моделирующей среде и использует систему смешанного моделирования в рамках одного проекта.

Анализ различных моделей показывает, что наиболее перспективной является модель Джилса-Атертона [1].

Разработанная Джилсом и Атертоном теория ферромагнитного гистерезиса разделяет в функции насыщения обратимое и необратимое намагничивание [2]. Полное намагничивание согласно модели Джилса-Атертона показано на рисунке 1.

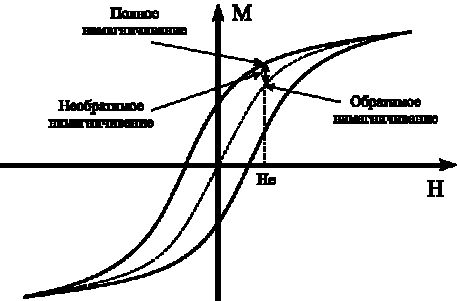
$F:\Магистратура 1курс\Статьи\2.png$

Рисунок 1 — Петля гистерезиса по модели Джилса-Атертона

Встроенная модель нелинейного сердечника core_ja в SystemVision основана на модификации модели Джилса-Атертона и имеет следующие параметры:

· K, А/м — постоянная необратимой деформации доменных стенок;

· C — постоянная упругого смещения доменных границ;

· M_S, А/м — намагниченность насыщения;

· α — параметр, учитывающий эффективную напряженность магнитного поля в сердечнике;

· А — параметр формы безгистерезисной кривой;

· AREA, м² — площадь поперечного сечения магнитопровода;

· PATH, м — средняя длина магнитной силовой линии.

Безгистерезисная кривая в модели core_ja задается с помощью гиперболического котангенса. Модель Джилса-Атертона, используемая в SystemVision, имеет некоторые отличия в численной реализации от классической модели, описанной J. P. A. Bastos, NelsonSadowski [3] (таблица 1).

Таблица 1 — Сравнение уравнений классической модели Джилса-Атертона и модели, используемой в SystemVision

Классическая модель Джилса-Атертона	SystemVisionMentorGraphics
— эффективное приложенное поле
M_A—безгистерезисная кривая намагничивания	M_A—безгистерезисная кривая намагничивания
, если ,, если
M_rev— обратимое намагничивание	M_rev— обратимое намагничивание
(использование значений из предыдущего шага расчета) M_irr— необратимое намагничивание	(использование значений из предыдущего шага расчета) M_irr— необратимое намагничивание


_M_―_{полное намагничивание}	_M_―_{полное намагничивание}

Подходы к моделированию магнитных компонентов в САПР, основанные на модели Джилса-Атертона, схожи и при определенном сочетании параметров дают одинаковый результат (рисунок 2), несмотря на некоторые отличия в уравнениях. Также встроенные модели САПР обладают общими достоинствами и недостатками, характерными для модели Джилса-Атертона:

· необходимость дополнительного расчета и подбора параметров модели по экспериментальным данным;

· при подборе параметров для точного моделирования предельных петель погрешность при моделировании частных петель может составлять сотни процентов;

· отсутствие зависимости формы петли от температуры, частоты или скорости перемагничивания;

· простота реализации модели и возможность добавления новых зависимостей, в том числе от скорости перемагничивания и температуры.

Уравнения классической модели Джилса-Атертона и модели, используемой в SystemVision (таблица 1), реализованы в MathCad для удобства подбора и сравнения характеристик.

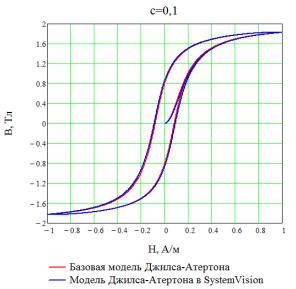
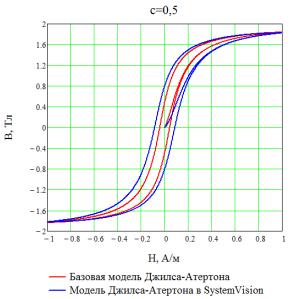
а б

Рисунок 2 — Сравнение петель гистерезиса, полученных с помощью базовой модели Джилса-Атертона и модели, используемой в SystemVision,

при разных значениях параметра с.

Модель Джилса-Атертона в целом адекватно отражает форму и поведение зависимости B(H). Однако функция безгистерезисной кривой в области насыщения растет достаточно медленно, и модель Джилса-Атертона завышает потери в сердечнике (рисунок 3,а).

Для устранения данного недостатка и коррекции гистерезисной кривой была введена дополнительная зависимость параметра К модели Джилса-Атертона от поля намагничивания [4]:

Введение такой зависимости позволяет получить предельную петлю гистерезиса, более приближенную к реальной только для конкретно заданных условий перемагничивания (рисунок 3,б). При коррекции параметра K происходит изменение основной кривой намагничивания, частные петли измеренным не соответствуют и имеют неправильный наклон. Для устранения этого недостатка и дальнейшей коррекции формы кривой предлагается другая зависимость от поля намагничивания:

_где0≤_x_≤1_.

Для получения экспериментальных петель были проведены измерения петель гистерезиса магнитопроводаК16х10х4,5 М2000НМ1 на частоте100кГц при максимальном поле намагничивания 20–300А/м и температуре 23°С.

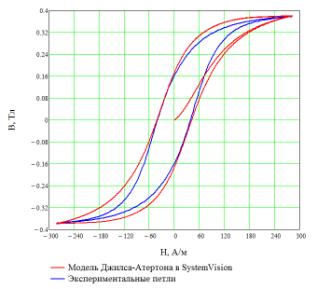
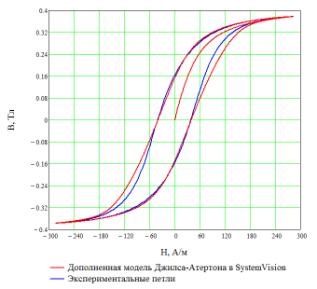
$M:\Диплом\Статья_3.jpg$ $M:\Диплом\Статья_2.jpg$

а б

Рисунок 3 — Предельные петли гистерезиса, полученные с помощью модели SystemVision и дополненной модели

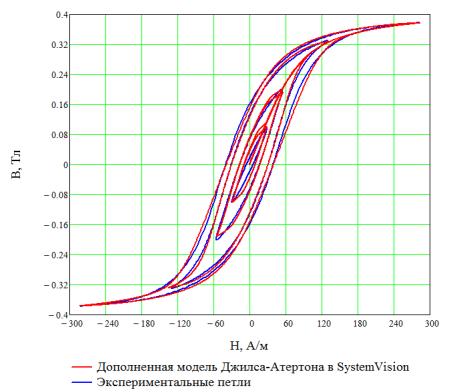
$M:\Диплом\Статья_1.jpg$

Рисунок 4 — Сравнение семейств петель гистерезиса, полученных экспериментально и с помощью дополненной модели

Сравнение семейств петель гистерезиса, полученных экспериментально и с помощью дополненной модели показывает, что частные петли имеют форму, соответствующую характеристикам реального образца (рисунок 4).

Литература

1. Каткова, А.А. Анализ математических моделей магнитных материалов // Сборник трудов X международной научно-технической конференции студентов и аспирантов 18-19 апреля 2013 г. "Информационные технологии, энергетика и экономика". В 3 т. Том 1. - Смоленск: Изд-во "Универсум", 2013. - С. 210-214.

2. D.C. Jiles, D.L. Atherton. Theory of ferromagnetic. Hysteresis Journal of Magnetism and Magnetic Materials, North-Holland, Amsterdam, 61 (1986), 48-60.

3. J. P. A. Bastos, N. Sadowski. Electromagnetic Modeling by Finite Element Methods. UniversidadeFederaldeSantaCatarina, Florianopolis, Brazil, 2003. - р. 497.

4. Peter Reid Wilson. Modeling and simulation of magnetic components in electric circuits. Department of electronics and computer science, November 2001. - p. 289.

CORRECTION METHOD OF A MAGNETIZATION CURVE IN JILES-ATHERTON FERROMAGNETIC CORE MODEL

Katkova A. A., Penkov A. A.

In work the method of correction of a magnetization curve in Jiles-Atherton model ferromagnetic core is offered. The offered method is based on introduction in model of the additional equations. For confirmation of improvement of a form of loops comparison with experimental characteristics for K16x10x4,5 M2000HM1 magnetic conductor at a frequency 100kHz is carried out.

Key words: Jiles-Atherton model, core, magnetization.

Филиал ФГБОУВПО «Национальный исследовательский университет МЭИ»

в г. Смоленске

Поступила в редакцию 12.12.2013.