Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 15. -
Вып. 1. - 2016. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-49-html/TITL-49.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-49-html/cont.htm
УДК 519.8
Способ калибровки
дифференциальной модели биологического
процесса с использованием алгоритмов нечёткой логики
© 2016 г. Клименко А. О.
Статья содержит описание разработанного
авторами алгоритма калибровки параметров модели биологического процесса с
применением нечёткой логики, а также
пример практического применения данного алгоритма в исследовании влияния
перерывов в лечении препаратом на вероятность достижения ответов.
Ключевые
слова: моделирование биологических процессов,
нечёткая логика, калибровка модели.
Введение. Хорошо известно, что влияние различных факторов, определяющих
характер биологического процесса, имеет взаимный и многовариантный характер. Одной
из наиболее распространённых форм представления их взаимовлияния в модели
является система дифференциальных уравнений. Мы будем рассматривать частный
случай, когда имеется некоторое множество упорядоченных по времени наблюдённых
значений двух показателей, модель взаимосвязи между
которыми требует калибровки.
Целью работы является предложение математического способа моделирования
взаимосвязи между динамикой двух биологических показателей. Предложенный способ
должен решать присущие области
применения проблемы отсутствия сведений относительно формы функциональной аппроксимации
каждого из показателей и неполноты данных, получение которых зачастую связано с объективными трудностями.
Результаты
исследования. Был разработан алгоритм
и применён для калибровки модели в конкретной области – при исследовании
зависимости эффективности лечения препаратом иматиниб
от наличия перерывов в его осуществлении. Алгоритм калибровки включает следующие шаги.
1. По данным наблюдений имеем k=1…T элементов
динамического ряда y(t), за оценку dy(t)/d(t) при t=k примем величину:
dy0(t)=y(k)-y(k-1). Рассчитаем
элементы универсумов Ey={eyj} и Et={eti}. В качестве элементов принимаются упорядоченные по
возрастанию границы интервалов заданной длины, на которые разбивается область возможных
значений dy и t соответственно.
2. По данным выборки рассчитываются элементы матрицы
нечёткого перехода R. Rij соответствует доле в общем числе значений dy0 на
отрезке [eti-1, eti ] таких значений, которые принадлежат отрезку [eyj-1,eyj].
3. Рассматривая
ряд значений {Rij, i=1..M} как динамический ряд наблюдённых значений некоторой неизвестной функции g(i),i=1..,M, методами
математической статистики аппроксимируем
её полиномом 4-й степени fp(t), таким, что при t=i/M*T, fp(t)=g(i). В итоге в
качестве функции fy(t), аппроксимирующей dy/dt получаем формулу:
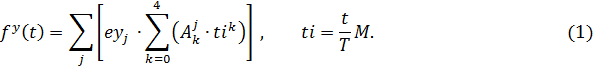
Заметим,
что хотя 4-я степень полинома не всегда
даёт точное приближение, однако взвешенная по eyj сумма полиномов 4-й степени обеспечивает требуемую точность во всех
рассмотренных нами конкретных случаях, когда такое приближение давала процедура
нечёткого перехода, которая сама даёт весьма близкое приближение. В то же время, очевидно, что формула (1) получена
в соответствии с логикой и алгоритмом нечёткого вывода.
Пример
практического применения. Предложенный
способ калибровки модели применим для
обработки данных и подтверждения выводов исследования [1] относительно роли перерывов в лечении
иматинибом. В данном исследовании влияние перерывов, которые описываются качественной величиной (есть-нет),
оценивается с помощью таких
показателей как вероятность наступления в заданный момент
времени цитогенетического и молекулярного ответов. Нас интересовал только
полный цитогенетический ответ (ПЦГО) и связанные с этой частью исследования
данные. Статистической базой является
вероятность достижения ПЦГО, которая рассчитана на определённые моменты времени с точностью до интервала,
величина интервала варьирует от 0 до 67% от
вероятности. По данным, приведённым в [1], применяя предложенный способ,
были построены модельные функции зависимости
вероятности достижения ПЦГО от времени для двух случаев – при наличии и при
отсутствии перерывов в лечении. Следует
отметить следующее обстоятельство. Поскольку разброс выборочных данных велик относительно
разброса значений функции, то прямое использование выборочных оценок производной может дать неправильный результат и поэтому было использовано усреднение и вычисление
скользящего среднего для n производных , рассчитанных в последовательные
моменты времени как разница подверженных случайному разбросу в заданных
интервалах величин. Эти проблемы не
возникают при точечных, а не интервальных данных. Модельные значения функции y рассчитаем по формуле y0(t)=y0(t-1)+fy(t). Значения y(t), где t – изменяется
непрерывно, рассчитывается посредством кусочно-линейного приближения. В результате
расчётов было получено приближённое описание производной вероятности достижения
ПЦГО для двух случаев (с перерывами лечения
x0(t) и без перерывов y0(t)):
fy(ti) =-0,000007ti4+0,0002ti3-0,0021ti2+0,0055ti+0,0156,
R2(y,y0)=0.987; (2)
fx (ti)=0,000004 ti4-0,0001ti3+0,0006ti2-0,0013ti+0,0127,
R2(x,x0)=0,99. (3)
Ey={0,004;0,012;0,019}
, Ey={0,003,008,013} , Et={0,25T,
0,5T, 0,75T,T}
Выводы. Вывод,
сделанный в [1] относительно определенного и существенного влияния перерывов в
лечении, подтверждается. Уравнения (2) и
(3) позволяют построить приближение функции dy/dx – функцию df(t), расчёты показали, что эта функция возрастает и
затем снижается, точка перегиба соответствует моменту, указанному в [1, стр.829] как наиболее показательный :“Особенно
заметно влияние перерывов в течение первого года терапии. Так, у пациентов с
перерывами продолжительностью более 30 дней вероятность достижения БЦГО и ПЦГО
после 6 и 12 месяцев терапии в 2 раза меньше, чем у пациентов без перерывов.”
Заметим, что наибольшую полезность предложенный способ
имеет в ситуации, когда динамика показателей может быть различной и меняться,
но неизменно соотношение между характером динамики одной величины и другой. В
этом случае данные не позволят построить аппроксимацию зависимости от
показателя каждого показателя, но позволят построить такую аппроксимацию сразу
для fd(t), и это знание
при возможности управления показателем x позволит целенаправленно влиять на y. Поскольку fd(t)=dy/dx, то y определяется интегрированием уравнения dy/dt=fd(t)*dx/dt=f(t).
Заключение. Современный
математический аппарат, такой как нечётко-множественное моделирование, получил
широкое распространение во многих областях и , с нашей
точки зрений, может быть с успехом применён в моделировании биологических
процессов.
ЛИТЕРАТУРА
1. Куцев
С. И., Шатохин Ю. В. Влияние перерывов терапии иматинибом
на достижение цитогенетического и молекулярного
ответов у больных хроническим миелолейкозом // Казанский медицинский журнал. - 2009. - № 90(6) . – С. 827–31.
Method of calibration of
differential model of biological process with use of algorithms of fuzzy logic
Klimenko A. O.
Article contains
the description of the algorithm of calibration of parameters of model of
biological process developed by authors with application of fuzzy logic, and
also an example of practical application of this algorithm in research of influence
of breaks in treatment by a preparation on probability of achievement of
answers.
Key words: modeling of biological
processes, fuzzy logic, calibration of model.
Клименко
Александра Олеговна, кандидат экономических наук,
доцент
МБОУ СОШ №14 (г. Новочеркасск).
Klimenko Alexandra Olegovna
School №14 (Novocherkassk)
МБОУ СОШ №14
(г. Новочеркасск).
Поступила в редакцию 11.01.2016.